【面试经典150题】跳跃游戏
题目链接
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
- 1 <= nums.length <= 1 0 4 10^4 104
- 0 <= nums[i] <= 1 0 5 10^5 105
分析:
假设当前位于nums[i],表示该元素后面的nums[i]个元素任我跳,那该跳哪个呢?
是不是得考虑跳到哪一个位置下下一步可以跳得更远。这个由index+nums[i]决定。
也就是说后面的nums[i]个元素里,哪个索引+元素值最大就跳到哪里。
/*** @param {number[]} nums* @return {boolean}*/
var canJump = function (nums) {let i = 0;let nextIndex;let maxVal = 0;while (i + nums[i] < nums.length - 1) {if (nums[i] === 0) {return false;}for (let j = i + 1; j <= i + nums[i]; j++) {if (j + nums[j] > maxVal) {nextIndex = j;maxVal = j + nums[j];}}maxVal = 0;i = nextIndex;}return true;
};
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度太高,换个思路:
维护一个最大可达位置maxReach。
/*** @param {number[]} nums* @return {boolean}*/
var canJump = function (nums) {let maxReach=0;for(let i=0;i<nums.length;i++){if(i>maxReach){return false;}maxReach=Math.max(maxReach,i+nums[i]);if(maxReach>=nums.length-1){return true;}}return true;
};
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
相关文章:

【面试经典150题】跳跃游戏
题目链接 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 1 < nums…...

【Rust】003-基础语法:流程控制
【Rust】003-基础语法:流程控制 文章目录 【Rust】003-基础语法:流程控制一、概述二、if 表达式1、语法格式2、多个3、获取表达式的值 三、循环1、loop:无限循环,可跳出无限循环跳出循环返回值 2、while:条件循环&…...
0829【综述】面向时空数据的区块链研究综述
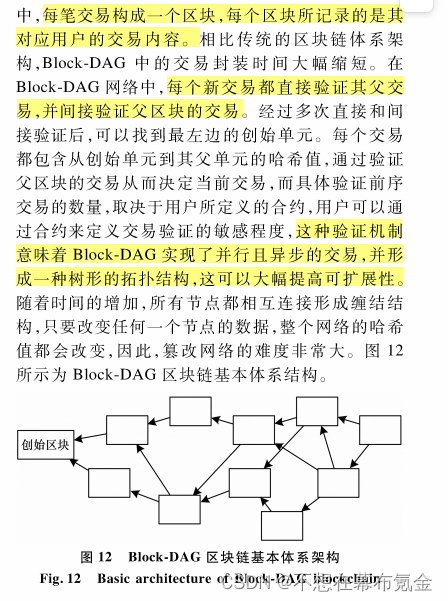
摘要:时空数据包括时间和空间2个维度,常被应用于物流、供应链等领域。传统的集中式存储方式虽然具有一定的便捷性,但不能充分满足时空数据存储及查询等要求,而区块链技术采用去中心化的分布式存储机制,并通过共识协议来保证数据的安全性。研究现有区块链1.0、2.0和以Block-DAG为…...
MySQL高级篇(SQL优化、索引优化、锁机制、主从复制)
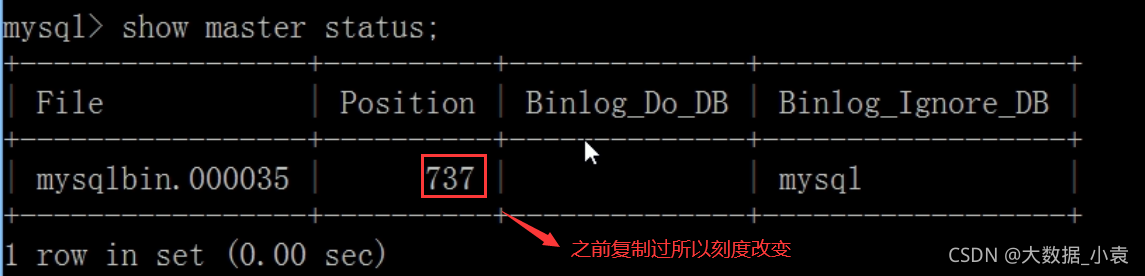
目录 0 存储引擎介绍1 SQL性能分析2 常见通用的JOIN查询 SQL执行加载顺序七种JOIN写法3 索引介绍 3.1 索引是什么3.2 索引优劣势3.3 索引分类和建索引命令语句3.4 索引结构与检索原理3.5 哪些情况适合建索引3.6 哪些情况不适合建索引4 性能分析 4.1 性能分析前提知识4.2 Expla…...

YOLOV8模型使用-检测-物体追踪
这个最新的物体检测模型,很厉害的样子,还有物体追踪的功能。 有官方的Python代码,直接上手试试就好,至于理论,有想研究在看论文了╮(╯_╰)╭ 简单介绍 YOLOv8 中可用的模型 YOLOv8 模型的每个类别中有五个模型用于检…...

springmvc:设置后端响应给前端的json数据转换成String格式
设置spring-mvc.xml: xml <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:context"http://www.springframework.org/schema/context"xmlns:xsi"http://www.w…...

Mac安装brew、mysql、redis
mac安装brew mac安装brewmac安装mysql并配置开机启动mac安装redis并配置开机启动 mac安装brew 第一步:执行. /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"第二步:输入开机密码 第三…...
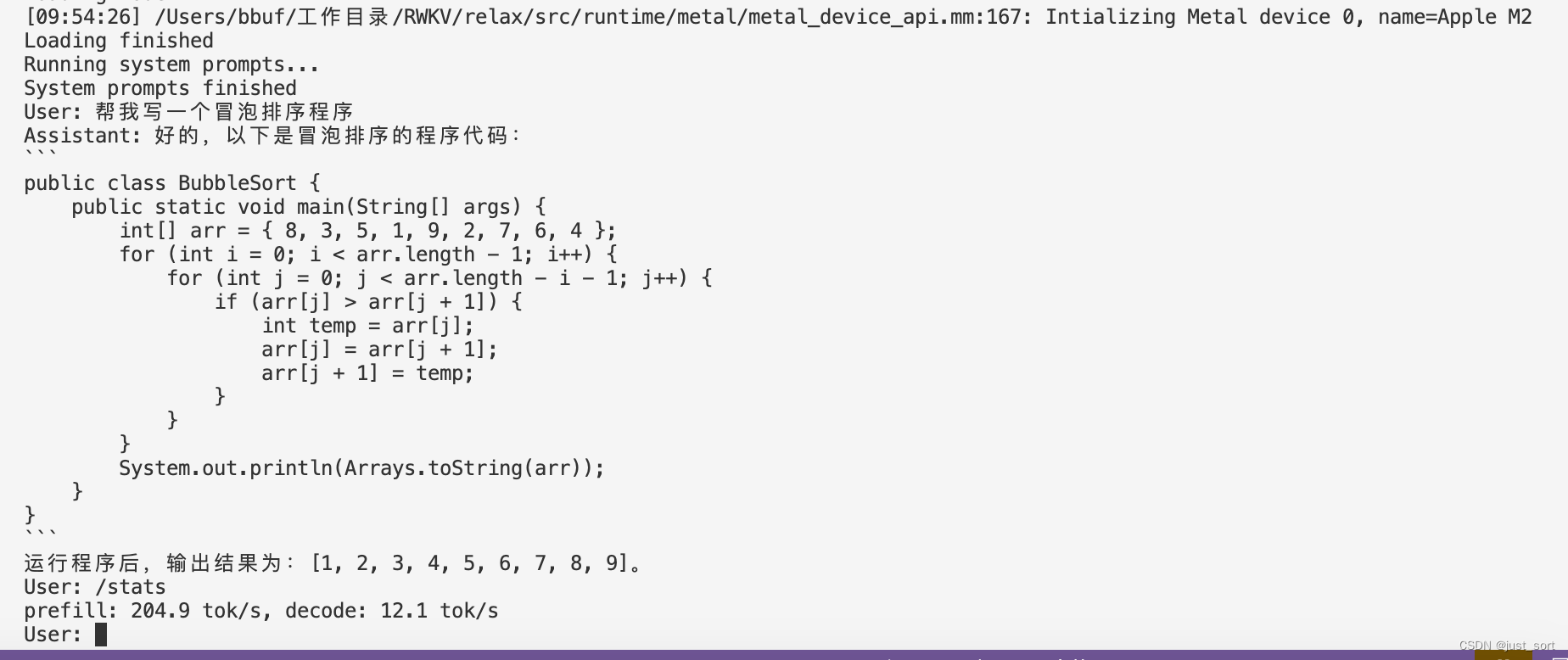
MLC-LLM 部署RWKV World系列模型实战(3B模型Mac M2解码可达26tokens/s)
0x0. 前言 我的 ChatRWKV 学习笔记和使用指南 这篇文章是学习RWKV的第一步,然后学习了一下之后决定自己应该做一些什么。所以就在RWKV社区看到了这个将RWKV World系列模型通过MLC-LLM部署在各种硬件平台的需求,然后我就开始了解MLC-LLM的编译部署流程和…...

Unity 之 参数类型之值类型参数的用法
文章目录 基本数据类型结构体结构体的进一步补充 总结: 当谈论值类型参数时,我们可以从基本数据类型和结构体两个方面详细解释。值类型参数指的是以值的形式传递给函数或方法的数据,而不是引用。 基本数据类型 基本数据类型的值类型参数&…...
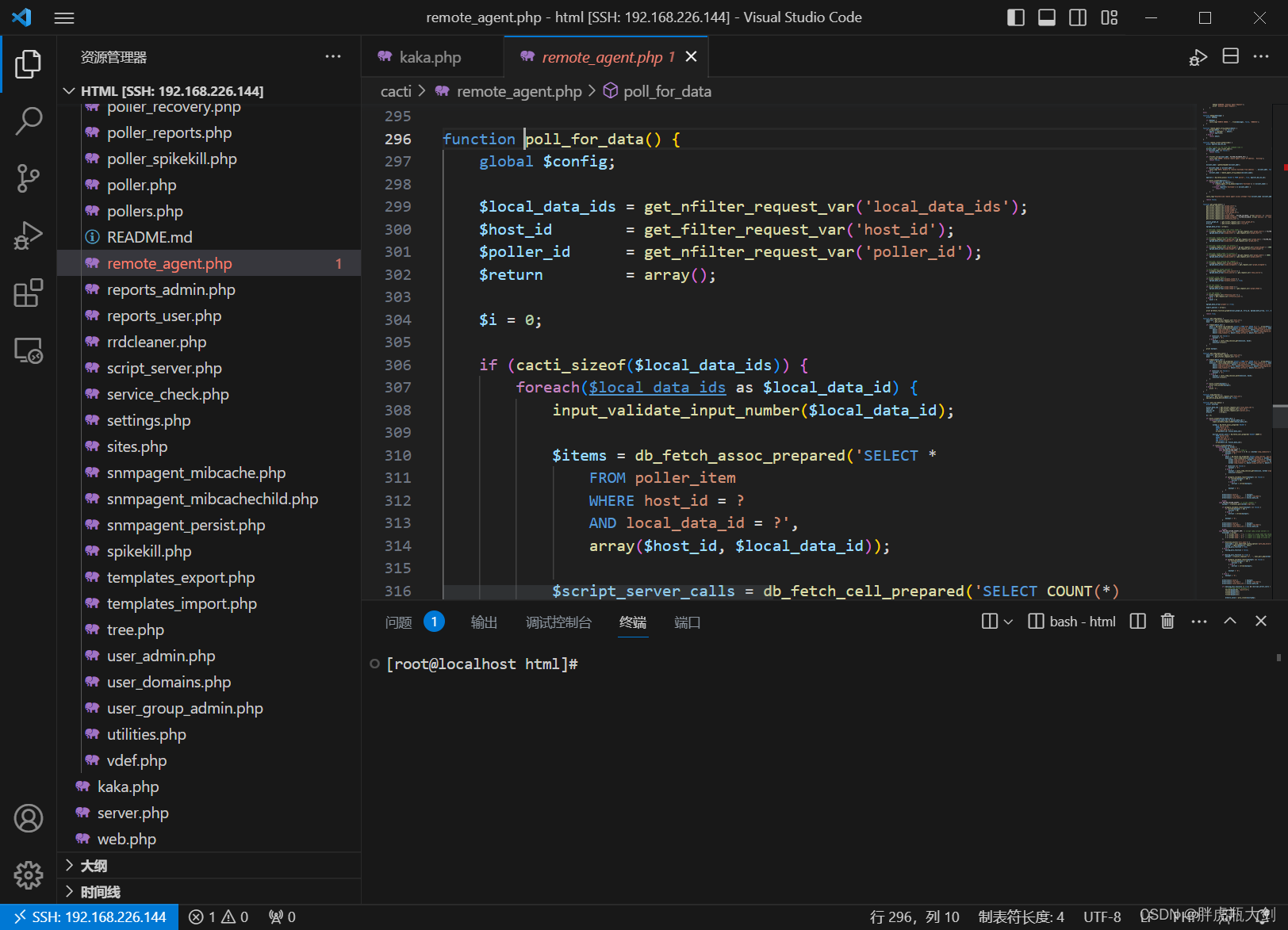
VScode远程连接主机
一、前期准备 1、Windows安装VSCode; 2、在VSCode中安装PHP Debug插件; 3、安装好Docker 4、在容器中安装Xdebug ①写一个展现phpinfo的php文件 <?php phpinfo(); ?>②在浏览器上打开该文件 ③复制所有信息丢到Xdebug: Installation instr…...

【iOS】属性关键字
文章目录 前言一、深拷贝与浅拷贝1、OC的拷贝方式有哪些2. OC对象实现的copy和mutableCopy分别为浅拷贝还是深拷贝?3. 自定义对象实现的copy和mutableCopy分别为浅拷贝还是深拷贝?4. 判断当前的深拷贝的类型?(区别是单层深拷贝还是完全深拷贝…...
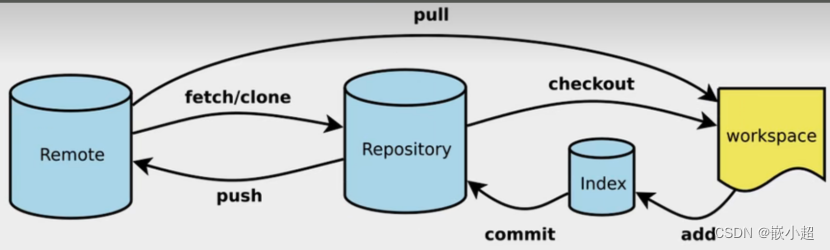
【计算机基础】Git从安装到使用,详细每一步!扩展Github\Gitlab
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
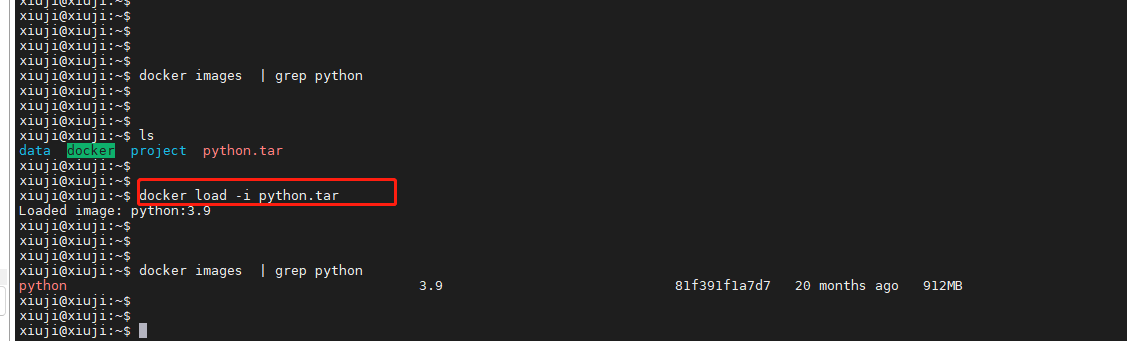
深入了解Docker镜像操作
Docker是一种流行的容器化平台,它允许开发者将应用程序及其依赖项打包成容器,以便在不同环境中轻松部署和运行。在Docker中,镜像是构建容器的基础,有些家人们可能在服务器上对docker镜像的操作命令不是很熟悉,本文将深…...

嵌入式开发-单片机学习介绍
一、单片机入门篇 单片机的定义和历史 单片机是一种集成了微处理器、存储器、输入输出接口和其他功能于一体的微型计算机,具有高度的集成性和便携性。单片机的历史可以追溯到20世纪70年代,随着微电子技术的不断发展,单片机逐渐成为了工业控…...
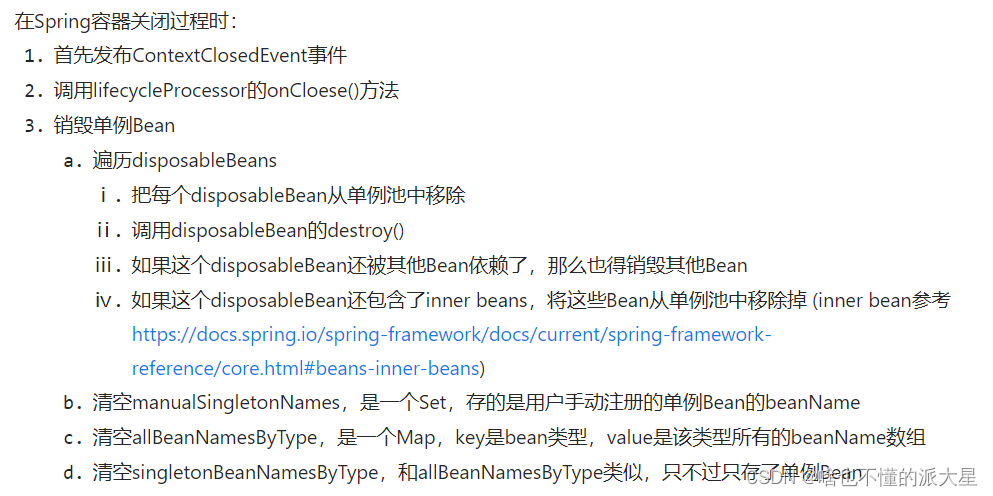
5、Spring之Bean生命周期源码解析(销毁)
Bean的销毁过程 Bean销毁是发送在Spring容器关闭过程中的。 在Spring容器关闭时,比如: AnnotationConfigApplicationContext context = new AnnotationConfigApplicationContext(AppConfig.class); UserService userService = (UserService) context.getBean("userSe…...

开发多点触控MFC应用程序
当下计算机变得越来越智能化,越来越无所不能,触摸屏的普及只是时间问题了。 虽然鼠标和键盘不会很快就离开人们的视野,毕竟人们使用鼠标跟键盘已经成为一种习惯,但是处理信息或者说操作计算机的其他方法也层出不穷——比如触控技术…...

使用nlohmann json库进行序列化与反序列化
nlohmann源码仓库:https://github.com/nlohmann/json使用方式:将其nlohmann文件夹加入,包含其头文件json.hpp即可demo #include <iostream> #include "nlohmann/json.hpp" #include <vector>using json nlohmann::js…...
)
高教社杯数模竞赛特辑论文篇-2012年A题:葡萄酒的评价(附获奖论文)
目录 摘 要 一、问题重述 二、问题分析 2.1 问题一的分析 2.2 问题二的分析...

手写RPC——数据序列化工具protobuf
手写RPC——数据序列化工具protobuf Protocol Buffers(protobuf)是一种用于结构化数据序列化的开源库和协议。下面是 protobuf 的一些优点和缺点: 优点: 高效的序列化和反序列化:protobuf 使用二进制编码,…...
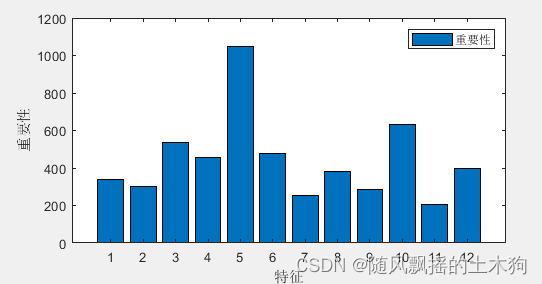
【MATLAB第70期】基于MATLAB的LightGbm(LGBM)梯度增强决策树多输入单输出回归预测及多分类预测模型(全网首发)
【MATLAB第70期】基于MATLAB的LightGbm(LGBM)梯度增强决策树多输入单输出回归预测及多分类预测模型(全网首发) 一、学习资料 (LGBM)是一种基于梯度增强决策树(GBDT)算法。 本次研究三个内容,分别是回归预测,二分类预测和多分类预…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
