Leetcode 面试题 17.01 不用加号的加法

设计一个函数把两个数字相加。不得使用 + 或者其他算术运算符。
示例:
输入: a = 1, b = 1 输出: 2
提示:
a,b均可能是负数或 0- 结果不会溢出 32 位整数
我的答案:
一、信息
1.设计一个函数把两个数相加
2.不得使用+或者其他运算符
3.a,b均为负数或0
4.结果不会溢出32位整数
二、分析
问题出现:
1.如何实现不用加法就实现两数相加呢?
我的思路:
思路1:通过将a,b转化成二进制,这样我们就能用二进制加法求解了。
新的问题出现:
该如何实现二进制加法呢?
首先我们可以观察二进制加法的规律
1101
+1010
10111
规律就是:
1 0 得1
1 1 得0
0 0 得0
我的答案其实很简单我们只需要通过与异或运算即可实现
问题2:该如何避免结果不会溢出32位整数呢?
我的实现:
为了不使用`+`或其他算术运算符来实现数字的加法,我们可以使用位操作。以下是基于此思路的解决方案:
### 1. C语言:
#include <stdio.h>int add(int a, int b) {while (b != 0) {unsigned int carry = (unsigned int)(a & b) << 1; // 计算进位a = a ^ b; // 不计算进位的加法b = carry; // 把进位放在b上,继续进行加法}return a;
}int main() {int a = 1, b = 1;printf("Sum: %d\n", add(a, b));return 0;
}2. C++:
#include <iostream>int add(int a, int b) {while (b != 0) {unsigned int carry = (unsigned int)(a & b) << 1;a = a ^ b;b = carry;}return a;
}int main() {int a = 1, b = 1;std::cout << "Sum: " << add(a, b) << std::endl;return 0;
}JAVA:
public class AddWithoutPlus {public static int add(int a, int b) {while (b != 0) {int carry = a & b; // 计算进位a = a ^ b; // 不计算进位的加法b = carry << 1; // 把进位放在b上,继续进行加法}return a;}public static void main(String[] args) {int a = 1, b = 1;System.out.println("Sum: " + add(a, b));}
}
这些解决方案都是基于二进制表示的加法原理,利用位操作来实现的。当我们加两个二进制数时,可以分为两步:1) 不计算进位的加法,和 2) 计算进位。
英雄师傅的分析:
将a和b都转化成二进制以后,执行相加,举个简单的例子,例如a是21(二进制是10101),b是12(二进制是1100),它们两个相加的值应该是33
对于两个数的对应相加,如果不产生进位就是异或的结果。(在我看来就是用异或来模拟这个过程)
比如说:
唯一没有提到的,就是1和1相加的情况,这种情况会产生进位,所以异或结果并不等于相加的结果,但是异或的结果等于相加后低位的值。换言之1+1=10,异或结果等于0,0和0相等,很合理。
基于上述观点,如果两个数二进制在相加的过程中,都没有出现1和1的情况,那么加法就等于两个数的异或。如果有进位,那么就要把进位的那部分单独拎出来。
什么时候有进位呢?当两个都为1的时候,也就是两个位与为1的时候,所以我们可以把a+b拆成两个部分
a^b和a&b
英雄师傅的实现过程:
int add(int a, int b){if(b==0){return a;}return add(a^b,((unsigned int)(a&b))<<1);
}
Leetcode 题解
Leetcode地址:Leetcode题解
方法一:位运算
预备知识
有符号整数通常用补码来表示和存储,补码具有如下特征:
正整数的补码与原码相同;负整数的补码为其原码除符号位外的所有位取反后加 111。
可以将减法运算转化为补码的加法运算来实现。
符号位与数值位可以一起参与运算。
思路和算法
虽然题目只要求了不能使用算术运算符,但是原则上来说也不宜使用类似的运算符 +=\texttt{+=}+= 和 -=\texttt{-=}-= 以及 sum\texttt{sum}sum 等方法。于是,我们使用位运算来处理这个问题。
首先,考虑两个二进制位相加的四种情况如下:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (进位)
可以发现,对于整数 aaa 和 bbb:
在不考虑进位的情况下,其无进位加法结果为 a⊕b\texttt{a} \oplus \texttt{b}a⊕b。
而所有需要进位的位为 a & b\texttt{a \& b}a & b,进位后的进位结果为 (a & b) << 1\texttt{(a \& b) << 1}(a & b) << 1。
于是,我们可以将整数 aaa 和 bbb 的和,拆分为 aaa 和 bbb 的无进位加法结果与进位结果的和。因为每一次拆分都可以让需要进位的最低位至少左移一位,又因为 aaa 和 bbb 可以取到负数,所以我们最多需要 log(max_int)\log (max\_int)log(max_int) 次拆分即可完成运算。
因为有符号整数用补码来表示,所以以上算法也可以推广到 000 和负数。
实现
在 C++\texttt{C++}C++ 的实现中,当我们赋给带符号类型一个超出它表示范围的值时,结果是 undefined\text{undefined}undefined;而当我们赋给无符号类型一个超出它表示范围的值时,结果是初始值对无符号类型表示数值总数取模的余数。因此,我们可以使用无符号类型来防止溢出。
在 Python\texttt{Python}Python 的实现中,因为 Python\texttt{Python}Python 的整数类型为是无限长的,所以无论怎样左移位都不会溢出。因此,我们需要对 Python\texttt{Python}Python 中的整数进行额外处理,以模拟用补码表示的 323232 位有符号整数类型。具体地,我们将整数对 2322^{32}2
32
取模,从而使第 333333 位及更高位均为 000;因为此时最终结果为用补码表示的包含符号位的 323232 位整数,所以我们还需要再次将其换算为 Python\texttt{Python}Python 的整数。
C++:
class Solution {
public:int add(int a, int b) {while (b != 0) {unsigned int carry = (unsigned int)(a & b) << 1;a = a ^ b;b = carry;}return a;}
};JAVA:
class Solution {public int add(int a, int b) {while (b != 0) {int carry = (a & b) << 1;a = a ^ b;b = carry;}return a;}
}
总结:
个人
从这个问题中,我们可以学到多方面的知识和技能:
1. **基础计算机科学知识**:这道题目介绍了如何使用位操作来模拟基本的算术运算,这反映了计算机在底层如何处理加法。
2. **递归和迭代思维**:即使在这样的问题中,递归和迭代的应用也是一个重要的思维模式。我们反复应用相同的逻辑,直到达到预期的结果。
3. **处理边界情况**:考虑到整数溢出和32位限制,这提醒我们在解决问题时总是要注意潜在的边界情况和限制。
4. **位操作技能**:位操作是许多算法和数据结构问题中的一个关键技能。这道题目为我们提供了一次实际应用的机会,加深了我们对`AND`、`XOR`、左移等操作的理解。
5. **创新思维**:当面对某些明显的方法(例如使用加法运算符)不可用时,寻找其他解决方案需要创新思维。这种思维方式对于不断发展的计算机科学领域是至关重要的。
6. **优化和效率**:尽管我们可以使用递归来解决此问题,但递归可能会导致效率问题,特别是对于大的整数。这提醒我们,即使某个方法是可行的,我们仍然需要考虑其效率。
7. **实际应用与理论知识**:在真实的计算机系统中,加法和其他算术操作确实是通过硬件逻辑(例如加法器)和位操作来实现的。通过这种方法,我们不仅学习了一种算法技巧,而且还深入了解了计算机的工作原理。
总的来说,这道题目为我们提供了一次深入学习计算机科学基础、算法设计和优化的机会,并激发了我们的创新思维。
感受:
其实这道题目和计算机组成原理中定点加法和减法这一章很像,象在哪里呢?其实就是像在对二进制加法的推导和探索,其中二者都处理了很多进位问题。其实我觉得出题人是想让我们体验一把当初计算机科学家们是如何一步一步设计出加法器的,就是绕开编译器原本就带着的+法函数而是自己写一个这个函数的底层。
(传送门:计算机组成原理 2.2 定点加法)

相关文章:

Leetcode 面试题 17.01 不用加号的加法
设计一个函数把两个数字相加。不得使用 或者其他算术运算符。 示例: 输入: a 1, b 1 输出: 2 提示: a, b 均可能是负数或 0结果不会溢出 32 位整数 我的答案: 一、信息 1.设计一个函数把两个数相加 2.不得使用或者其他运算符 3.a,b均为负数或…...
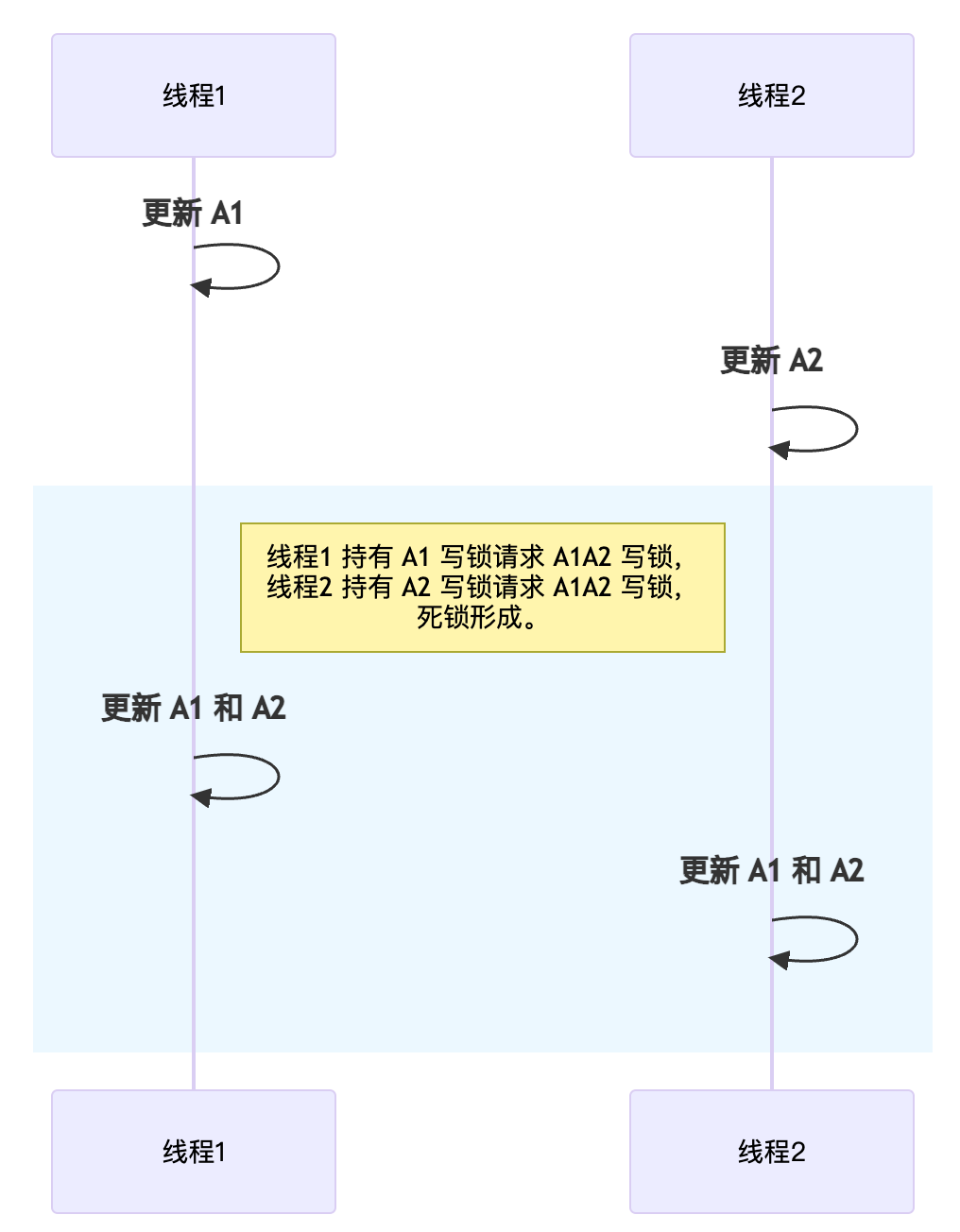
一个 MySQL 数据库死锁的案例和解决方案
本文介绍了一个 MySQL 数据库死锁的案例和解决方案。 场景 生产环境出了一个偶现的数据库死锁问题,导致少部分业务处理失败。 分析特征之后,发现是多个线程并发执行同一个方法,更新关联的数据时可能会出现,把场景简化概括一下&…...

AMBEO 双声道空间音频现已迈进直播制作领域
图片来源:Unsplash,作者:Bence Balla-Schottner AMBEO 双声道空间音频现已迈进直播制作领域 为所有观众解锁更加身临其境的听觉体验 森海塞尔将功能强大的 AMBEO 双声道空间音频技术引入了广播电视直播应用领域,对所有体育赛事广…...
在VSCode上画UML的三个插件
2023年9月2日,周六晚上 因为写代理模式的博客时需要画UML,所以就在网上找了半天, 最后觉得VSCode上的这三个插件比较好用 目录 三个画UML的VSCode插件PlantUMLDraw.io IntegrationUMLet我个人推荐使用PlantUML 三个画UML的VSCode插件 Pla…...

Springboot - 1.什么是springboot
👀Spring的核心模块 Spring Framework是一个功能强大的开源框架,用于构建Java企业级应用程序。它提供了多个核心模块,每个模块都提供不同的功能,用于解决应用程序开发中的各种问题。以下是Spring Framework的核心模块的全面解析&…...

学习微信小程序 Westore
最近,接到小程序需求,并且是在以前公司老项目上改造,打开项目,发现却不是我想象中的那样,不是上来就是 Page({}),而是create(store,{}),纳尼???这什么玩意&am…...
CentOS上使用Docker安装和部署kkFileView
🎈1 参考文档 kkFileView官方文档 🚀2 安装kkFileView 拉取Redis镜像。 docker pull keking/kkfileview启动docker容器。 docker run -it -d -p 8012:8012 keking/kkfileview --restart always解释: docker run redis # 从kkfileview镜像运行…...
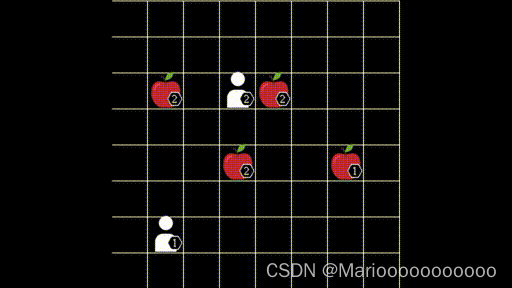
Level-based Foraging 多智能体游戏仿真环境
游戏场景测试 参考链接: https://kgithub.com/semitable/lb-foraging...

LeetCode-53-最大子数组和-贪心算法
贪心算法理论基础: 局部最优推全局最优 贪心无套路~ 没有什么规律~ 重点:每个阶段的局部最优是什么? 题目描述: 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素&#…...

解决gitee仓库中 .git 文件夹过大的问题
最近,许多项目都迁移到gitee。使用的也越来越频繁,但是今天突然收到一个仓库爆满的提示。让我一脸懵逼。本文将详细为你解答,这种情况如何处理。 1、起因 我收到的报错如下: remote: Powered by GITEE.COM [GNK-6.4] remote: T…...
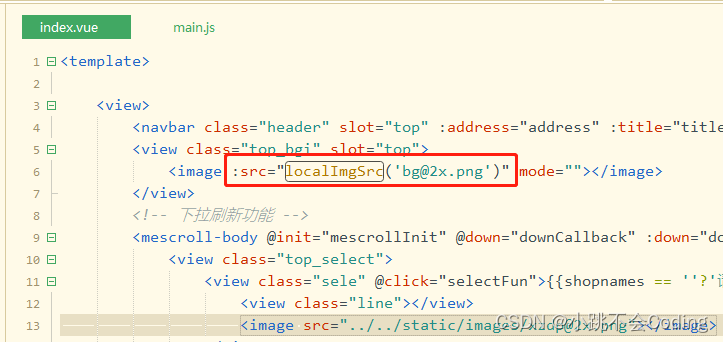
uniapp 开发小程序,封装一个方法,让图片使用线上地址
1.在main.js文件中,添加以下代码: 复制使用: // 图片使用网络地址 Vue.prototype.localImgSrc function(img){//项目的地址域名,例如百度return "https://baidu.cn/static/index/images/" img; }2.在页面中直接使用&…...
)
Android 12 源码分析 —— 应用层 三(SystemUIFactory及其Dependency解析)
Android 12 源码分析 —— 应用层 三(SystemUIFactory及其Dependency解析) 在上一篇文章中,介绍了SystemUI的启动流程,并且简单提及了Dagger2用来管理各个SystemUI中要用的依赖。而这部分代码就在:mContextAvailableC…...

考前冲刺上岸浙工商MBA的备考经验分享
2023年对于许多人来说都是不平凡的一年,历经三年的抗争,我们终于成功结束了疫情。而我也很幸运的被浙工商MBA项目录取,即将开始全新的学习生活。身为一名已在职工作6年的人,能够重回校园真是一种特别令人激动的体验。今天…...

XmlDocument.SelectNodes 不起作用
今天采用Xpath读取Xml节点,怎么都读不出。 问题分析: 错误代码如下: XmlDocument xmlD new XmlDocument();xmlD.PreserveWhitespace true;xmlD.LoadXml(xStr);xmlD.SelectNodes("job-scheduling-data/schedule/job");经排查 do…...
部署单点elasticsearch
部署elasticsearch 创建网络 因为我们还需要部署kibana容器,因此需要让es和kibana容器互联。这里先创建一个网络 docker network create es-net 拉取镜像 我们采用elasticsearch的7.12.1版本的镜像 docker pull elasticsearch:7.12.1 运行 运行docker命令&a…...

ElementUI浅尝辄止16:Tag 标签
用于标记和选择。 1.如何使用? 由type属性来选择tag的类型,也可以通过color属性来自定义背景色。<el-tag>标签一</el-tag> <el-tag type"success">标签二</el-tag> <el-tag type"info">标签三</e…...
框架)
Java虚拟机(JVM)框架
见:GitHub - eHackyd/Java_JVM: Java虚拟机(JVM)框架的学习笔记...

配置Publisher 的编译规则
步骤 1:创建ROS Package 使用以下命令创建一个新的ROS软件包: catkin_create_pkg my_publisher_package roscpp std_msgs步骤 2:编辑 CMakeLists.txt 文件 打开您的ROS软件包的 CMakeLists.txt 文件,通常位于软件包的根目录。您…...

【SpringBoot】接口实现:SpringBoot实现博客系统的文章列表页接口代码
以下是一个简单的Spring Boot博客系统的文章列表页接口代码示例: java RestController RequestMapping("/articles") public class ArticleController {Autowiredprivate ArticleService articleService;GetMapping("/")public List<Artic…...

如何使用SQL系列 之 如何在SQL中插入数据
简介 结构化查询语言,通常被称为SQL,在允许您将数据插入表中方面提供了极大的灵活性。例如,你可以使用VALUES关键字指定单独的行数据,使用SELECT查询从现有表中复制整组数据,以及以使SQL自动插入数据的方式定义列。 …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
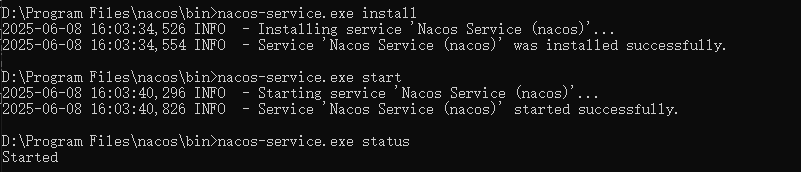
Windows开机自动启动中间件
WinSW(Windows Service Wrapper 是一个开源的 Windows 服务包装器,它可以帮助你将应用程序打包成系统服务,并实现开机自启动的功能。 一、下载 WinSW 下载 WinSW-x64.exe v2.12.0 (⬇️ 更多版本下载) 和 sample-minimal.xml 二、配置 WinS…...
)
Kafka 消息模式实战:从简单队列到流处理(一)
一、Kafka 简介 ** Kafka 是一种分布式的、基于发布 / 订阅的消息系统,由 LinkedIn 公司开发,并于 2011 年开源,后来成为 Apache 基金会的顶级项目。它最初的设计目标是处理 LinkedIn 公司的海量数据,如用户活动跟踪、消息传递和…...
