机器人中的数值优化(七)——修正阻尼牛顿法
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
九、修正阻尼牛顿法
1、基本牛顿方法
(1)基本牛顿方法介绍
Newton方法是Newton型方法的基础.本文主要讨论基本Newton方法、阻尼Newton方法及修正Newton方法的构造与性质.这类方法适宜于解决中小型最优化问题.
设f(x)具有连续的二阶偏导数,当前迭代点是 x k x_k xk,f(x)在 x k x_k xk处的Taylor展式为
f ( x k + d ) = f k + ∇ f ( x k ) T d + 1 2 d T ∇ 2 f ( x k ) d + o ( ∥ d ∥ 2 ) . f(x_k+d)=f_k+\nabla f\left(x_{k}\right)^\mathrm{T}d+\dfrac12d^{\mathrm T}\nabla^2 f(x_k) d+o(\|d\|^2). f(xk+d)=fk+∇f(xk)Td+21dT∇2f(xk)d+o(∥d∥2).
其中 d = x − x k d= x - x_k d=x−xk ,在点 x k x_k xk的邻域内,用如下二次函数来近似 f ( x k + d ) f(x_k + d) f(xk+d),求解问题
q k ( d ) ≜ f k + ∇ f ( x k ) T d + 1 2 d T ∇ 2 f ( x k ) d q_k(d)\triangleq f_k+ \nabla f\left(x_{k}\right)^\mathrm{T}d+\dfrac12d^{\mathrm T}\nabla^2 f(x_k)d qk(d)≜fk+∇f(xk)Td+21dT∇2f(xk)d
上式中的d也就是 x − x k x-x_k x−xk,所以上式也可写为如下的形式:
q k ( d ) ≜ f ( x k ) + ∇ f ( x k ) T ( x − x k ) + 1 2 ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) q_k(d)\triangleq f(\boldsymbol{x}_{k})+\nabla f(\boldsymbol{x}_{k})^{T}(\boldsymbol{x}-\boldsymbol{x}_{k})+{\frac{1}{2}}(\boldsymbol{x}-\boldsymbol{x}_{k})^{T}\nabla^{2}f(\boldsymbol{x}_{k})(\boldsymbol{x}-\boldsymbol{x}_{k}) qk(d)≜f(xk)+∇f(xk)T(x−xk)+21(x−xk)T∇2f(xk)(x−xk)

只要上式中的 ∇ 2 f ( x k ) \nabla^2f(x_k) ∇2f(xk)在 x k x_k xk处是正定的,就可以对上式求导,即求梯度等于0的点,得到以下方程组:
∇ 2 f ( x k ) ( x − x k ) + ∇ f ( x k ) = 0 \nabla^2f(\boldsymbol{x}_k)(\boldsymbol{x}-\boldsymbol{x}_k)+\nabla f(\boldsymbol{x}_k)=\boldsymbol{0} ∇2f(xk)(x−xk)+∇f(xk)=0
即:
∇ 2 f ( x k ) d = − ∇ f ( x k ) \nabla^2 f(x_k) d=-\nabla f\left(x_{k}\right) ∇2f(xk)d=−∇f(xk)
若 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)正定,则方程组的解 d k = − ∇ 2 f ( x k ) − 1 ∇ f ( x k ) d_k=-\nabla^2 f(x_k)^{-1}\nabla f\left(x_{k}\right) dk=−∇2f(xk)−1∇f(xk)为上述问题的唯一解,因为基本牛顿法步长取1,因此其迭代式为: x k + 1 = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) \boldsymbol{x}_{k+1}=\boldsymbol{x}_{k}-\left[\nabla^{2}\boldsymbol{f}(\boldsymbol{x}_{k})\right]^{-1}\nabla f(\boldsymbol{x}_{k}) xk+1=xk−[∇2f(xk)]−1∇f(xk)。

–
由上图可以看出通过不断迭代,可以很快收敛到局部最优解,此外,若目标函数 f ( x ) f(x) f(x)本来就是一个二次函数,其泰勒展开式 q k ( d ) q_k(d) qk(d)近似于它自己,此时,采用牛顿方向,就可以从任何地方经过一次迭代就能到达局部最优解。
所以,对于严格正定的二次函数,采用牛顿方向(步长),可以一步收敛到精确解。
我们称方程组 ∇ 2 f ( x k ) d = − ∇ f ( x k ) \nabla^2 f(x_k) d=-\nabla f\left(x_{k}\right) ∇2f(xk)d=−∇f(xk)为Newton方程,由该方程组得到的方向 d p d_p dp为Newton方向.用Newton方向作为迭代方向的最优化方法称为Newton方法.用Newton方法迭代的意义如下图所示,其中粗虚线表目标函数 f ( x ) f(x) f(x)的等高线,细虚线表 q k ( d ) q_k(d) qk(d)的等高线。
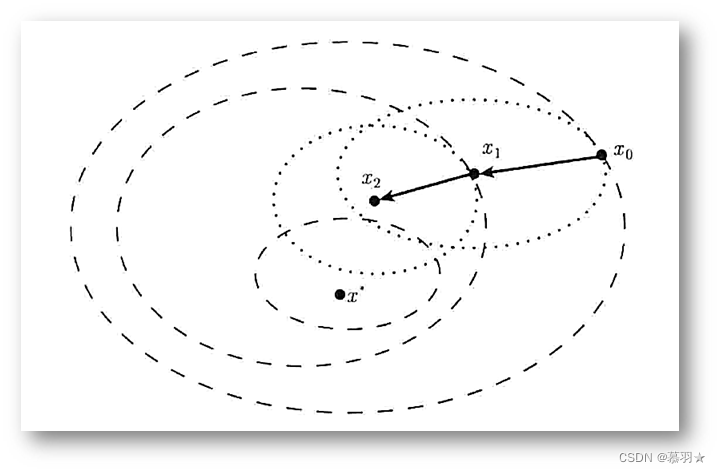
再例如下图中的例子,其中品红色曲线为 x 0 x_0 x0处的二次逼近的等值线,棕色曲线为 x 1 x_1 x1处的二次逼近的等值线

–
(2)基本牛顿方法算法流程
基本Newton方法指取全步长 a k = 1 a_k=1 ak=1的Newton方法, 下面给出基本Newton方法的迭代步骤:

此外,只要 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)正定,Newton方向 d k d_k dk就是下降方向,只要在 x k x_k xk(k=0,1,2,3,…)处 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)均正定,迭代就能不停的进行下去
附:判断一个矩阵是否是正定的方法
一个矩阵是正定的,当且仅当它是对称的(即等于它的转置矩阵)且所有特征值都是正数。特别地,一个正定矩阵是一个非奇异(可逆)矩阵。
判断一个矩阵是否是正定的方法有多种,以下是其中两种常用的方法:
方法① 判断所有特征值是否为正数:设矩阵 A A A 的特征值为 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn,则 A A A 是正定的当且仅当 λ i > 0 \lambda_i>0 λi>0 对于所有 i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i=1,2,⋯,n。
方法②判断所有主子矩阵的行列式是否为正数:设矩阵 A A A 的 k k k 阶主子矩阵为 A k A_k Ak,即 A k A_k Ak 由 A A A 的前 k k k 行和前 k k k 列组成,则 A A A 是正定的当且仅当 A k A_k Ak 的行列式 det ( A k ) > 0 \det(A_k)>0 det(Ak)>0 对于所有 k = 1 , 2 , ⋯ , n k=1,2,\cdots,n k=1,2,⋯,n。
需要注意的是,这些方法只适用于实对称矩阵,而对于复数矩阵,需要使用其他定义和方法来判断是否是正定的。
一个简单的牛顿法例子如下(拖动或者双击可查看大图):

下面给出了其迭代过程,并与采用恒定步长0.1的梯度下降法进行了对比,从收敛速度来看,牛顿法更优,从稳定性和占用计算资源来看,牛顿法不占优,如果该凸函数的Hesse矩阵是严格正定的就可以满足稳定性,如果有高效的求解Hesse矩阵的方法,就可以减少计算资源的占用。

一般从以下三个方面评价一种数值优化方法:
①、收敛速度:一般认为在对数精度曲线上随着迭代次数的增加,呈直线下降,一般认为收敛较快,如果是朝下的二次曲线,则认为收敛速度更快,如果是朝上的曲线,则认为收敛速度不佳。
②、适用于不同函数时的稳定性:有的要求是强凸的或者凸的,有的可以适应于非凸的函数,甚至是非光滑的函数,甚至是不连续的函数。
③、每次迭代的计算量:每次迭代需要计算多大的计算量,一般跟维度和约束个数有关,一般可用收敛速度和计算量(计算耗时)的乘积来衡量
(3)基本牛顿方法收敛性
Newton方法的收敛性依赖于初始点的选择.当初始点接近极小点时,迭代序列收敛于极小点,并且收敛很快; 否则就会出现迭代序列收敛到鞍点或极大点的情形,或者在迭代过程中出现矩阵奇异或病态的情形,使线性方程组不能求解或不能很好地求解,导致迭代失败.
由基本Newton方法的收敛性定理可知,只有当迭代点充分接近a*时,基本Newton方法的收敛性才能保证。
(4)基本牛顿方法的优缺点
优点:
(1)当 x 0 x_0 x0充分接近问题的极小点x * 时,方法以二阶收敛速度收敛;
(2)方法具有二次终止性.
缺点:
(1)当 x 0 x_0 x0没有充分接近问题的极小点x * 时, ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)会出现不正定或奇异的情形,使{ x k x_k xk}不能收敛到x * ,或使迭代无法进行; 即使 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)正定也不能保证{ f k f_k fk}单调下降。
(2)每步迭代需要计算Hesse矩阵,即计算n(n +1)/2个二阶偏导数.
(3)每步迭代需要解一个线性方程组,计算量为O( n 3 n^3 n3) 。
(4)在很多非凸的函数中曲率可能不是正向的曲率,即使Hesse矩阵是半正定的也会出现奇异值是0的情况,不能对Hesse矩阵求逆也就完成不了一次迭代,因此需要规避Hesse矩阵奇异或者不定的情况,才能快速收敛。
(5)只有当Hesse是正定的时候,它的逆才是正定的,此时乘以一个负梯度方向才能保证牛顿方向与负梯度方向夹角是小于90度的,若Hesse是不定的,则夹角可能是钝角,此时,不能保证牛顿方向是下降方向。即我们要保证牛顿方向与最速下降方向夹角小于90度

2、阻尼牛顿方法
为改善Newton方法的局部收敛性质,我们可以采用带一维搜索的Newton方法,即
x k + 1 = x k + α k d k x_{k+1}=x_{k}+\alpha_k d_k xk+1=xk+αkdk
其中 a k a_k ak 是一维搜索的结果.该方法称为阻尼Newton方法.此方法能够保证对正定的 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk),{ f k f_k fk}单调下降;即使 x k x_k xk离 x ∗ x^* x∗稍远,该方法产生的点列{ x k x_k xk}仍可能收敛至 x ∗ x^* x∗
对严格凸函数,采用Wolfe 准则的阻尼Newton方法具有全局收敛性,且采用Wolfe准则的阻尼Newton方法产生的{ x k x_k xk}满足下列二者之一:
① { x k x_k xk}为有穷点列,即存在N,使得 ∇ f ( x N ) \nabla f\left(x_{N}\right) ∇f(xN)= 0;
② { x k x_k xk}为无穷点列, { x k x_k xk}收敛到 f f f的唯一极小值点 x ∗ x^* x∗
此外,采用精确线搜索、Goldstein 准则等线搜索准则,阻尼Newton方法对严格凸函数的全局收敛性亦存在.
3、修正阻尼牛顿方法(混合方法)
Newton方法在迭代的过程中会出现 Hesse矩阵奇异、不正定的情形,Newton方向会出现与梯度 ∇ f ( x k ) \nabla f\left(x_{k}\right) ∇f(xk)几乎正交的情形.为解决这些问题,人们提出了许多修正Newton方法.这些方法或采用与其他方法混合的方式,或采用隐式地、显式地对Hesse矩阵进行修正的方式对Newton方法进行修正.
笼统来说,修正阻尼牛顿法满足以下框架,其中M是对Hessian矩阵的近似,根据不同的情况,可以选择不同的近似方法,得到不同的M,多种方法组合在一起也就成了混合方法

–
(1)
最简单的修正 Newton方法是针对 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)可逆但不正定情形的.即当 ∇ f ( x k ) \nabla f\left(x_{k}\right) ∇f(xk) ∇ 2 f − 1 ( x k ) \nabla^2 f^{-1}(x_k) ∇2f−1(xk) ∇ f ( x k ) \nabla f\left(x_{k}\right) ∇f(xk) <0时,我们可以简单地取
d k = ∇ 2 f − 1 ( x k ) ∇ f ( x k ) d_k=\nabla^2 f^{-1}(x_k)\nabla f\left(x_{k}\right) dk=∇2f−1(xk)∇f(xk)
使 d k d_k dk是下降方向.然而这样的修正不能处理Newton方法可能遇到的各种情形,如下的混合方法可以处理Newton方法可能遇到的各种情形。
(2)一种混合方法
所谓的混合方法就是一种方法与另外一种或多种方法混合使用的方法.混合的方式有多种,混合的目的是取各方法所长,或者是在一种方法无法继续迭代下去时,采用另一种方法.使迭代得以继续进行.下面我们要考虑的方法是Newton方法与负梯度方法的混合.该方法采用Newton方向,但在 Hesse矩阵 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)奇异或 ∇ f ( x k ) \nabla f\left(x_{k}\right) ∇f(xk)与 d k d_k dk几乎正交时,采用负梯度方向;在 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)负定,但 ∇ 2 f − 1 ( x k ) \nabla^2 f^{-1}(x_k) ∇2f−1(xk)存在时,取 d k d_k dk= ∇ 2 f − 1 ( x k ) \nabla^2 f^{-1}(x_k) ∇2f−1(xk) ∇ f ( x k ) \nabla f\left(x_{k}\right) ∇f(xk).考虑到Newton方法在迭代过程中可能出现的各种情形,我们有如下算法:

该方法的缺点在于,若迭代过程中连续多步使用负梯度方向,收敛速度会趋于负梯度方法的收敛速度.虽然该方法不是非常有效的方法,然而为了让迭代进行下去,它所采用的混合方式还是有代表意义的。
(3)LM方法
LM (Levenberg-Marquardt)方法是处理 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)奇异、不正定等情形的一个最简单且有效的方法,它是指求解
( ∇ 2 f ( x k ) + ν k I ) d = − ∇ f ( x k ) (\nabla^2 f(x_k)+\nu_kI)d=-\nabla f\left(x_{k}\right) (∇2f(xk)+νkI)d=−∇f(xk)
来确定迭代方向的Newton型方法,这里 v k v_k vk >0,Ⅰ是单位阵.显然,若 v k v_k vk足够大,可以保证 ∇ 2 f ( x k ) + ν k I \nabla^2 f(x_k)+\nu_kI ∇2f(xk)+νkI正定,当 v k v_k vk很小时,上述方程的的解偏向于Newton方向,此时能够保证正定性,随着 v k v_k vk的增大,上述方程的解向负梯度方向偏移.这种修正Newton方法的思想来自解最小二乘问题的LM方法,在后续的文章中讨论关于修正 v k v_k vk的方法.这里当 ∇ 2 f ( x k ) + ν k I \nabla^2 f(x_k)+\nu_kI ∇2f(xk)+νkI不正定时,我们可以简单地取 v k v_k vk=2 v k v_k vk
当 ( ∇ 2 f ( x k ) + ν k I ) (\nabla^2 f(x_k)+\nu_kI) (∇2f(xk)+νkI)正定时可以对其进行Cholesky分解,分解成一个下三角阵乘一个上三角阵的形式,即 ( ∇ 2 f ( x k ) + ν k I ) (\nabla^2 f(x_k)+\nu_kI) (∇2f(xk)+νkI)= L L T LL^T LLT,其中L为下三角阵,通过Cholesky分解可以快速求出以上方程。
LM方法比 Newton方法有效,它能够处理Newton方法所不能处理的情况.
(4)
对于一般的非凸函数,它的Hessian矩阵是不定的,我们可以将Hessian矩阵进行Bunch-Kaufman因式分解,分解成 L B L T LBL^T LBLT,L为下三角阵,B为分块对角阵, L T L^T LT为上三角阵。假设B由1个1x1的对角块,和1个2x2的对角块组成。对于1x1的块,要求其为正数,对于2x2的块的两个特征值必然为1正1负,所以在将Hessian矩阵分解成 L B L T LBL^T LBLT后,将其中的B阵的2x2的块更改为与其最接近的正定阵,即2x2的块的两个特征值均为正,然后再利用修改后的方程求出迭代方向。

参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化
相关文章:

机器人中的数值优化(七)——修正阻尼牛顿法
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

程序员自由创业周记#3:No1.作品
作息 如果不是热爱,很难解释为什么能早上6点自然醒后坐在电脑前除了吃饭一直敲代码到23点这个现象,而且还乐此不疲。 之前上班的时候生活就很规律,没想到失业后的生活比之前还要规律;记得还在上班的时候,每天7点半懒洋…...

固定资产制度怎么完善管理?
固定资产管理制度的完善管理可以从以下几个方面入手: 建立完善的资产管理制度,可以及时掌握企业资产的信息状况,使资产管理更加明确,防止资产流失。 加大固定资产监管力度,从配置资产、使用资产到处置资产进行全…...

神经网络--感知机
感知机 单层感知机原理 单层感知机:解决二分类问题,激活函数一般使用sign函数,基于误分类点到超平面的距离总和来构造损失函数,由损失函数推导出模型中损失函数对参数 w w w和 b b b的梯度,利用梯度下降法从而进行参数更新。让1代表A类,0代…...
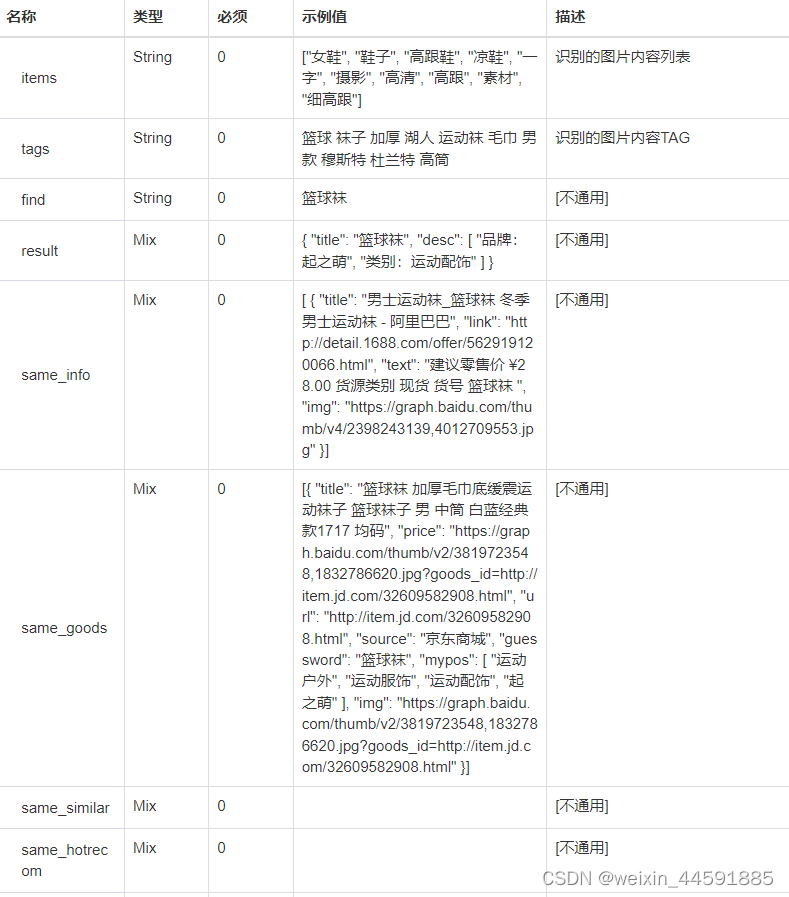
Java“牵手”1688图片识别商品接口数据,图片地址识别商品接口,图片识别相似商品接口,1688API申请指南
1688商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要通过图片地址识别获取1688商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问1688商城的网页来获取商品详情信息。以下是两种常…...

科技资讯|微软获得AI双肩包专利,Find My防丢背包大火
根据美国商标和专利局(USPTO)近日公示的清单,微软于今年 5 月提交了一项智能双肩包专利,其亮点在于整合了 AI 技术,可以识别佩戴者周围环境、自动响应用户聊天请求、访问基于云端的信息、以及和其它设备交互。 在此附…...

数学建模:多目标优化算法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:多目标优化算法 多目标优化 分别求权重方法 算法流程: 两个目标权重求和,化为单目标函数,然后求解最优值 min x ∑ i 1 m w i F i ( x ) s.…...

arcmap 在oracle删除表重新创建提示表名存在解决放啊
sde表创建是有注册或者是关联关系存在的 按照以下步骤删除表的数据 select t.* from sde.TABLE_REGISTRY t where table_name like IRR%; DELETE from sde.TABLE_REGISTRY where table_nameIRRIGATION_TYPE; select t.* from sde.LAYERS t where table_name like IRR%; DELET…...
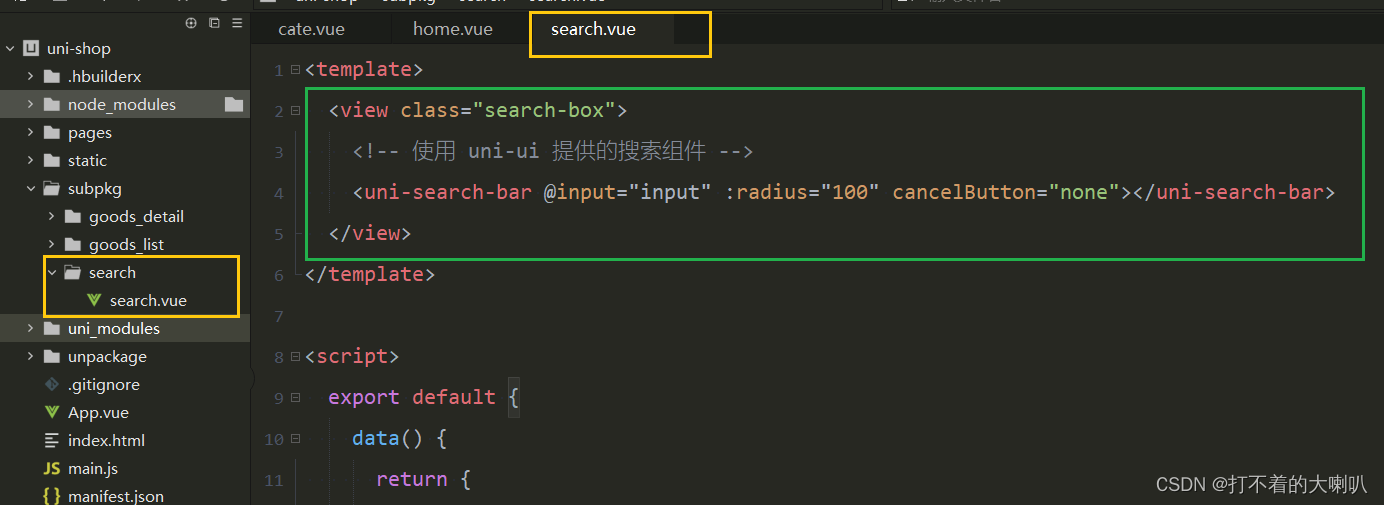
新版HBuilderX在uni_modules创建搜索search组件
1、创建自定义组件 my-search 新版HBuilder没有了 component 文件夹,但是有 uni_modules 文件夹,用来创建组件: 右键 uni_modules 文件夹,点击 新建uni_modules创建在弹出框,填写组件名字,例如:…...
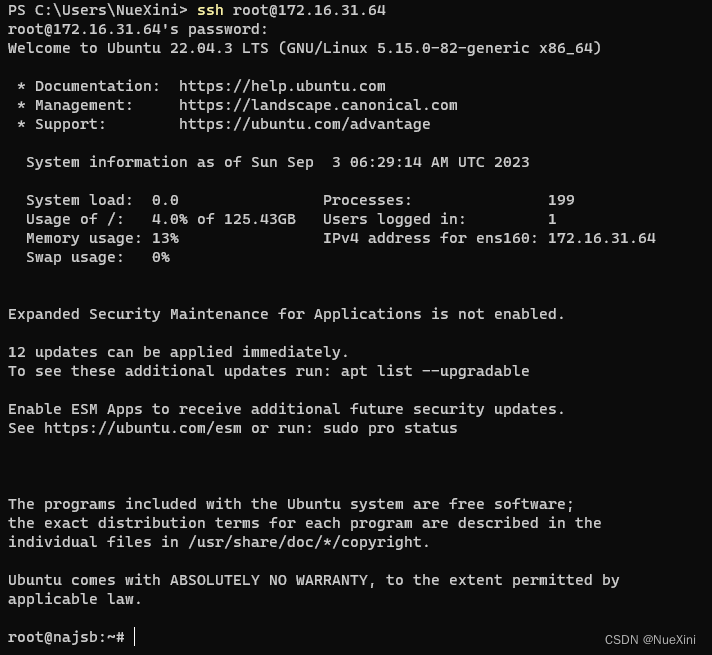
Ubutnu允许ssh连接使用root与密码登录
文章目录 1. 修改sshd_config2. 设置root密码3. 重启SSH服务 1. 修改sshd_config 修改/etc/ssh/sshd_config文件,找到 #Authentication,将 PermitRootLogin 参数修改为 yes。如果 PermitRootLogin 参数被注释,请去掉首行的注释符号ÿ…...
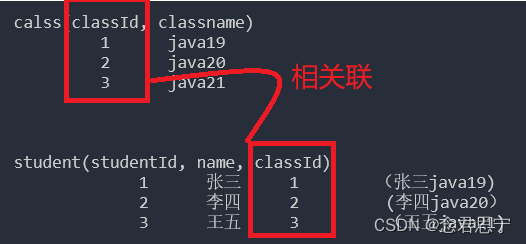
MySQL中表的设计
在MySQL中表的设计,需要一定的经验才能理解,由于笔者目前在读中,理解不是很深刻,仅根据自己的想法外界的一些参考资料做出下述文字描述,一些错误,请大佬及时指正~~ 在本篇文章中,介绍一点简单粗…...
UE4/5在蓝图细节面板中添加函数按钮(蓝图与c++的方法)
目录 在细节面板中添加按钮使用函数 蓝图的方法 事件 函数 效果 uec的方法 效果 在细节面板中添加按钮使用函数 很多时候,我们可以看到一些插件的actor类中,点击一下之后就可以实现如矩阵一样的效果。 实际上是因为其使用了函数来修改了蓝图中的数…...

Python爬虫乱码问题之encoding和apparent_encoding的区别
encoding是从http中的header中的charset字段中提取的编码方式,若header中没有charset字段则默认为ISO-8859-1编码模式,则无法解析中文,这是乱码的原因 apparent_encoding会从网页的内容中分析网页编码的方式,所以apparent_encodi…...

Docker技术--Docker简介和架构
1.Docker简介 (1).引入 我们之前学习了EXSI,对于虚拟化技术有所了解,但是我们发现类似于EXSI这样比较传统的虚拟化技术是存在着一定的缺陷:所占用的资源比较多,简单的说,就是你需要给每一个用户提供一个操作平台,这一个…...
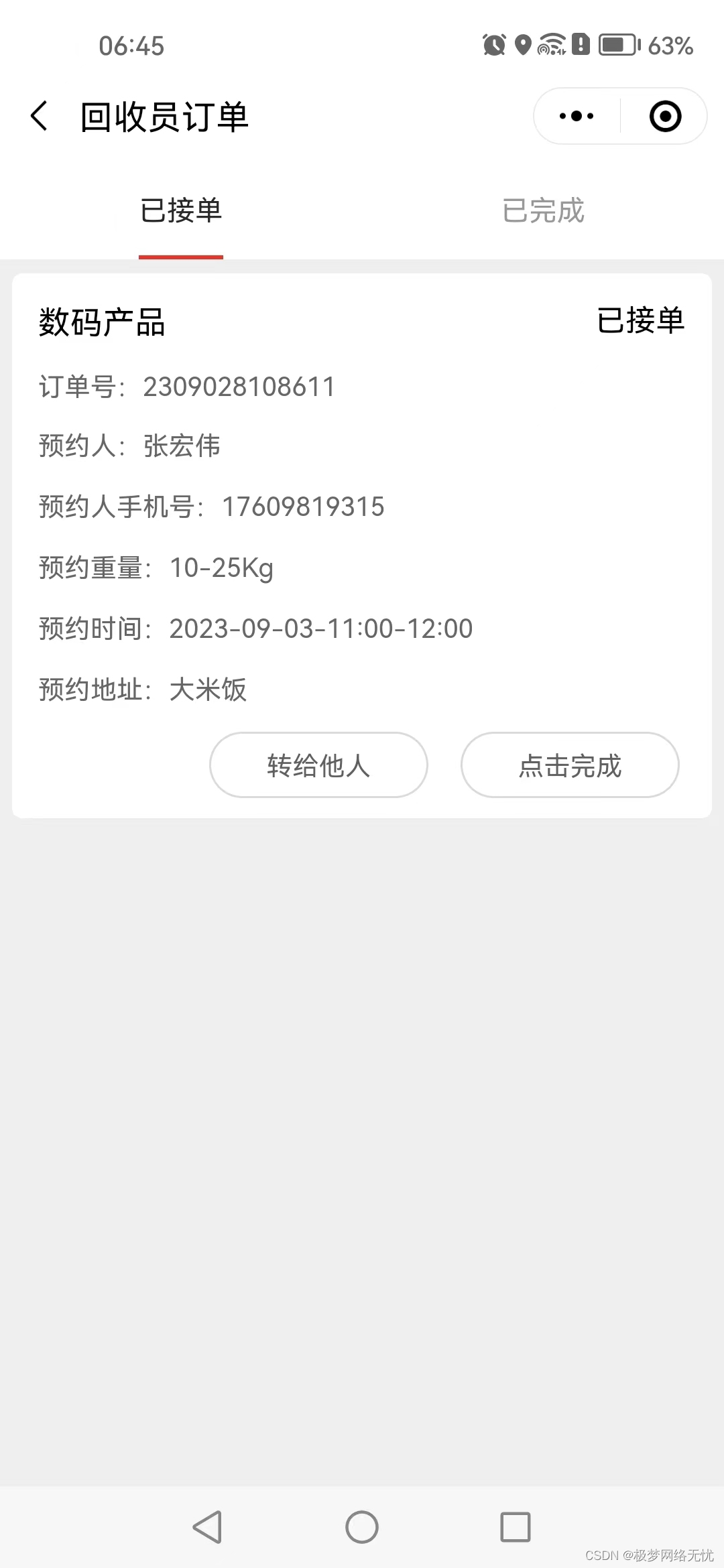
废品回收功能文档
废品回收 基础版 后台功能 功能字段描述二级分类表字段:图标、名称、描述、图片、注意事项、上一级、状态功能:前端展示和筛选;增删改查今日指导价表字段:关联分类、名称、价格、单位、状态功能:前端展示和预估价格&…...

【ARMv8 SIMD和浮点指令编程】NEON 乘法指令——asimdrdm
ARMv8 有许多版本(ARMv8.1 等),它们定义了强制和可选功能。Linux 内核通过 hwcaps 公开了其中一些功能的存在。这些值显示在 /proc/cpuinfo 中。 名称版本支持的特性fp-Single-precision and double-precision floating point.asimd-Advanced SIMD.evtstrmN/AGeneric timer …...
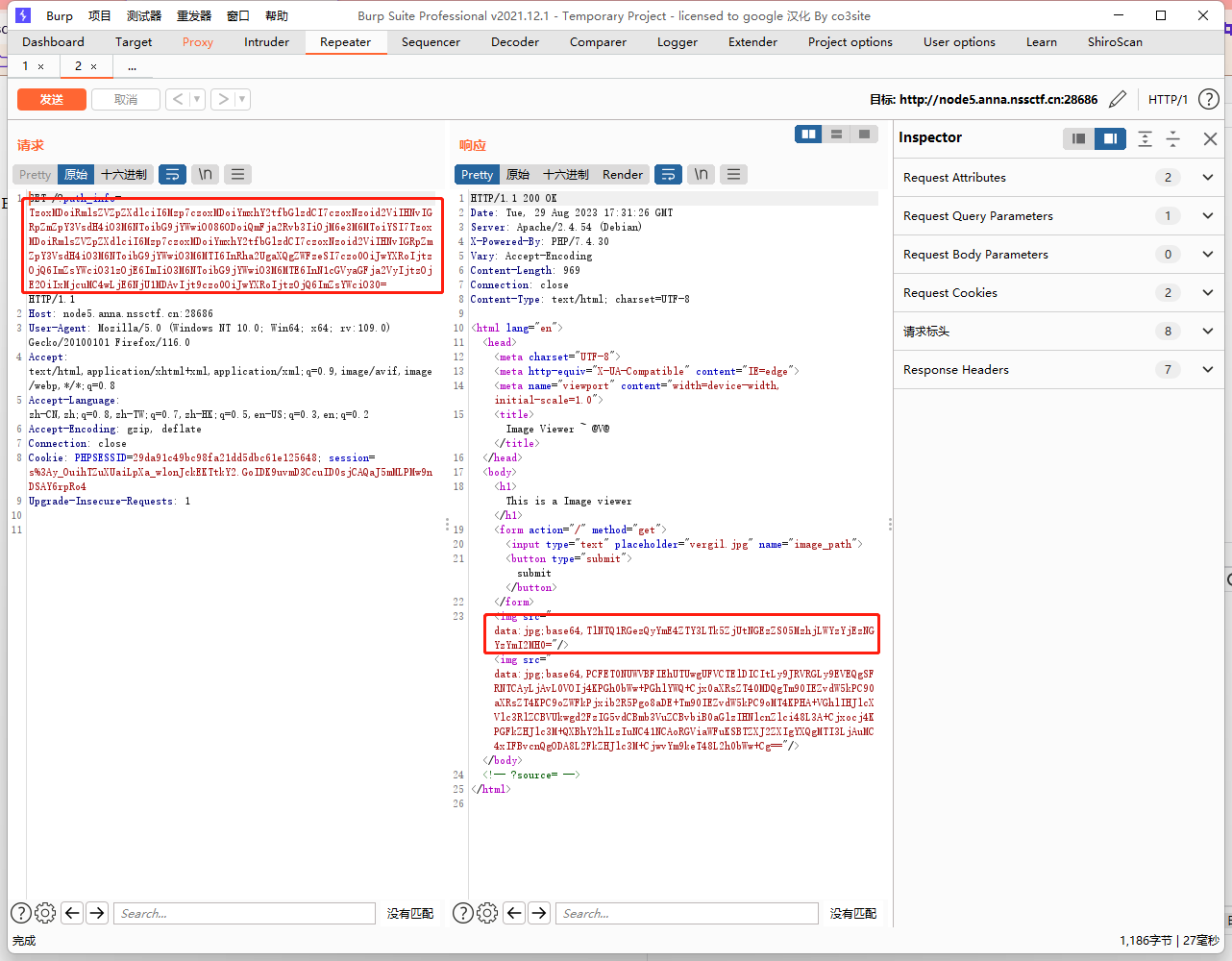
[SWPUCTF 2022]——Web方向 详细Writeup
SWPUCTF 2022 ez_ez_php 打开环境得到源码 <?php error_reporting(0); if (isset($_GET[file])) {if ( substr($_GET["file"], 0, 3) "php" ) {echo "Nice!!!";include($_GET["file"]);} else {echo "Hacker!!";} }e…...

Shell编程:流程控制与高级应用的深入解析
目录 Shell 流程控制 1、条件语句 2、循环语句 Shell 函数 Shell 输入/输出重定向 Shell 文件包含 文件包含的示例 Shell 流程控制 使用Shell编程时,流程控制是非常重要的,它允许你根据条件执行不同的命令或者控制程序的执行流程。Shell支持一些基…...
一文讲通嵌入式现状
近年来,随着计算机技术和集成电路技术的迅速发展,嵌入式技术在通讯、网络、工控、医疗、电子等领域日益普及,并发挥着越来越重要的作用。嵌入式系统已成为当前最为热门和前景广阔的IT应用领域之一。 随着信息化、智能化、网络化的不断推进&am…...

设计模式-代理模式Proxy
代理模式Proxy 代理模式 (Proxy)1) 静态代理1.a) 原理解析1.b) 使用场景1.c) 静态代理步骤总结 2) 动态代理2.a) 基于 JDK 的动态代理实现步骤2.b) 基于 CGLIB 的动态代理实现步骤2.c) Spring中aop的使用步骤 代理模式 (Proxy) 代理设计模式(Proxy Design Pattern&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
