神经网络--感知机
感知机
单层感知机原理
单层感知机:解决二分类问题,激活函数一般使用sign函数,基于误分类点到超平面的距离总和来构造损失函数,由损失函数推导出模型中损失函数对参数 w w w和 b b b的梯度,利用梯度下降法从而进行参数更新。让+1代表A类,0代表B类。
以下是原理示意图:

神经元会计算传送过来的信号的总和,当这个总和超过了阈值 θ θ θ时,才会输出1。这也称为“神经元被激活”。
二进制步进函数 y = { 1 , w T x + b > θ 0 , w T x + b < θ 二进制步进函数\\ y = \begin{cases} 1, w^Tx+b>\theta\\ 0, w^Tx+b<\theta \end{cases} 二进制步进函数y={1,wTx+b>θ0,wTx+b<θ
损失函数:基于误分类点到超平面的距离总和
点 ( x , y ) 到直线 ( A x + B y + C = w T x + b = 0 ) 距离 : d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ 点(x,y)到直线(Ax+By+C=w^Tx+b=0)距离:d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\frac{|w^Tx+b|}{||w||} 点(x,y)到直线(Ax+By+C=wTx+b=0)距离:d=A2+B2∣Ax0+By0+C∣=∣∣w∣∣∣wTx+b∣
L O S S = ∑ i = 1 m − y i ( w T x i + b ) LOSS = \sum_{i=1}^{m}{-{y_i(w^Tx_i+b)}} LOSS=i=1∑m−yi(wTxi+b)
∂ L o s s ∂ w = − ∑ i = 1 m y i x i ∂ L o s s ∂ b = − ∑ i = 1 m y i \frac{\partial Loss}{\partial w} = -\sum^{m}_{i=1}y_ix_i\\ \frac{\partial Loss}{\partial b} = -\sum^{m}_{i=1}y_i ∂w∂Loss=−i=1∑myixi∂b∂Loss=−i=1∑myi
感知机训练算法
∗ ∗ 算法 1 :感知机训练算法 ∗ ∗ 初始化参数 w = 0 , b = 0 r e p e a t : { 从训练集随机采样一个样本 ( x i , y i ) 计算感知机的输出 t = f ( w T x i + b ) , f ( x ) = 1 , x > 0 ; f ( x ) = 0 , x ≤ 0 如果 t ≠ y i : 更新权值 : w ← w + η ( y i − t ) x i 更新偏移量 : b ← b + η ( y i − t ) } u n t i l 训练次数达到要求输出 : 分类网络参数 w 和 b , 其中 η 为学习率。 **算法 1:感知机训练算法**\\ 初始化参数 w= 0, b= 0\\ repeat:\{ 从训练集随机采样一个样本(x_i, y_i) \\ 计算感知机的输出 t = f(w^T x_i + b),f(x)=1,x>0; f(x)=0, x \leq 0\\ 如果t ≠ y_i:\\ 更新权值:w ← w + \eta (y_i-t)x_i \\ 更新偏移量:b ← b + \eta (y_i-t)\\ \}until 训练次数达到要求 输出:分类网络参数w和b,其中\eta 为学习率。 ∗∗算法1:感知机训练算法∗∗初始化参数w=0,b=0repeat:{从训练集随机采样一个样本(xi,yi)计算感知机的输出t=f(wTxi+b),f(x)=1,x>0;f(x)=0,x≤0如果t=yi:更新权值:w←w+η(yi−t)xi更新偏移量:b←b+η(yi−t)}until训练次数达到要求输出:分类网络参数w和b,其中η为学习率。
单层感知机返回的 w T + b = 0 w^T+b=0 wT+b=0构成一条直线,这也是单层感知机的局限,可以实现与门、与非门(与门取反)、或门三种逻辑电路,无法实现异或门(XOR,(与非门和或门)的与 )逻辑电路.

反向传播算法

正确理解误差反向传播法,有两种方法:
一种是基于数学式—微分链;
另一种是基于计算图(computational graph),直观地理解误差反向传播法。
计算图

在计算图上,从左向右进行计算是正方向上的传播,简称为正向传播(forward propagation)。正向传播是从计算图出发点到结束点的传播。当然从图上看,从右向左的传播,称为反向传播(backward propagation)。反向传播在导数计算中发挥重要作用。

假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额,即求“支付金额关于苹果的价格的导数”。这个导数的值表示当苹果的价格稍微上涨时,支付金额会增加多少。反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。在这个例子中,反向传播从右向左传递导数的值(1→1.1→2.2)。从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。这意味着,如果苹果的价格上涨1元,最终的支付金额会增加2.2元(严格地讲,如果苹果的价格增加某个微小值,则最终的支付金额将增加那个微小值的2.2倍)
链式法则


加法节点

乘法节点


激活节点
1.relu

2.sigmoid函数
计算图的反向传播:
-
步骤1:
“/”节点表示 y = 1 x y=\frac{1}{x} y=x1,它的导数可以解析性地表示为: ∂ y ∂ x = − 1 x 2 = − y 2 \frac{\partial y}{\partial x} = -\frac{1}{x^2} = -y^2 ∂x∂y=−x21=−y2 。反向传播时,会将上游的值乘以−y2(正向传播的输出的平方乘以−1后的值)后,再传给下游。计算图如下所示。

-
步骤2:
“+”节点将上游的值原封不动地传给下游。计算图如下所示.

-
步骤3:
“exp”节点表示: y = e x p ( x ) y = exp(x) y=exp(x),它的导数: ∂ y ∂ x = e x p ( x ) \frac{\partial y}{\partial x} = exp(x) ∂x∂y=exp(x)。
计算图中,上游的值乘以正向传播时的输出(例中是exp(−x))后,再传给下游。

-
步骤4: “×”节点将正向传播时的值翻转后做乘法运算。因此,这里要乘以−1。

这里要注意,反向传播的输出 ∂ L ∂ y y 2 e x p ( − x ) \frac{\partial L}{\partial y}y^2exp(-x) ∂y∂Ly2exp(−x),这个值只根据正向传播时的输入x和输出y就可以算出来。
因此,计算图可以画成集约化的“sigmoid”节点。

简洁版的计算图可以省略反向传播中的计算过程,因此计算效率更高。
∂ L ∂ y y 2 e x p ( − x ) = ∂ L ∂ y y ( 1 − y ) \frac{\partial L}{\partial y}y^2exp(-x) = \frac{\partial L}{\partial y}y(1-y) ∂y∂Ly2exp(−x)=∂y∂Ly(1−y)
因此,Sigmoid 层的反向传播,只根据正向传播的输出就能计算出来。

(3)Affine层 (np.dot())
矩阵的乘积运算在几何学领域被称为“仿射变换”Affine。因此,使用仿射变换的处理实现为“Affine层”

相关文章:

神经网络--感知机
感知机 单层感知机原理 单层感知机:解决二分类问题,激活函数一般使用sign函数,基于误分类点到超平面的距离总和来构造损失函数,由损失函数推导出模型中损失函数对参数 w w w和 b b b的梯度,利用梯度下降法从而进行参数更新。让1代表A类,0代…...
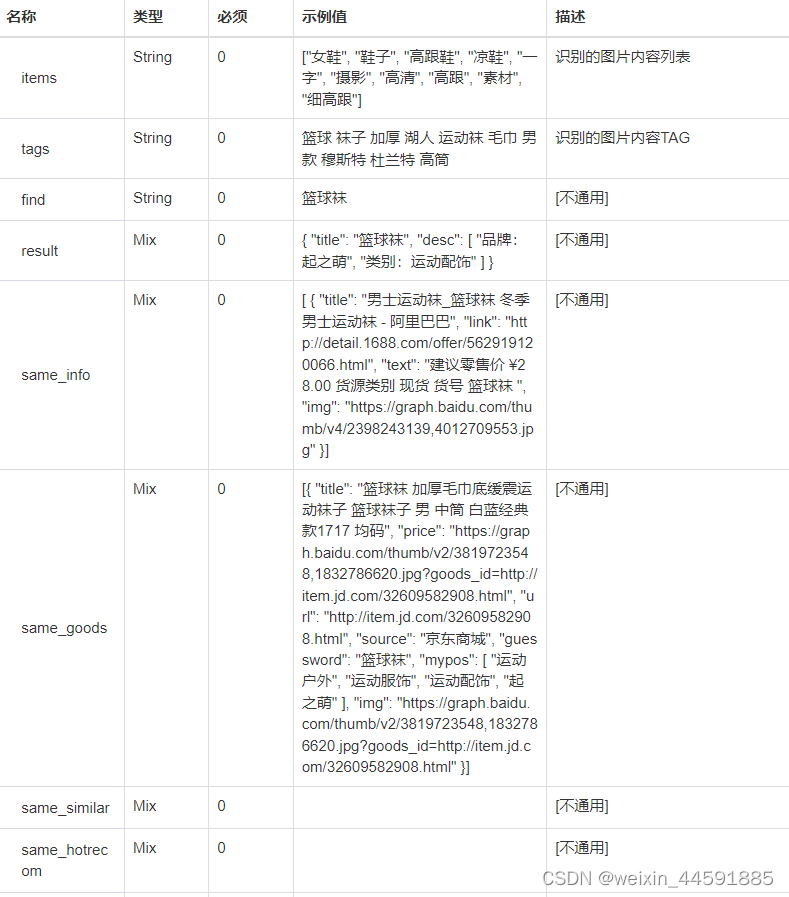
Java“牵手”1688图片识别商品接口数据,图片地址识别商品接口,图片识别相似商品接口,1688API申请指南
1688商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要通过图片地址识别获取1688商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问1688商城的网页来获取商品详情信息。以下是两种常…...

科技资讯|微软获得AI双肩包专利,Find My防丢背包大火
根据美国商标和专利局(USPTO)近日公示的清单,微软于今年 5 月提交了一项智能双肩包专利,其亮点在于整合了 AI 技术,可以识别佩戴者周围环境、自动响应用户聊天请求、访问基于云端的信息、以及和其它设备交互。 在此附…...

数学建模:多目标优化算法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:多目标优化算法 多目标优化 分别求权重方法 算法流程: 两个目标权重求和,化为单目标函数,然后求解最优值 min x ∑ i 1 m w i F i ( x ) s.…...

arcmap 在oracle删除表重新创建提示表名存在解决放啊
sde表创建是有注册或者是关联关系存在的 按照以下步骤删除表的数据 select t.* from sde.TABLE_REGISTRY t where table_name like IRR%; DELETE from sde.TABLE_REGISTRY where table_nameIRRIGATION_TYPE; select t.* from sde.LAYERS t where table_name like IRR%; DELET…...
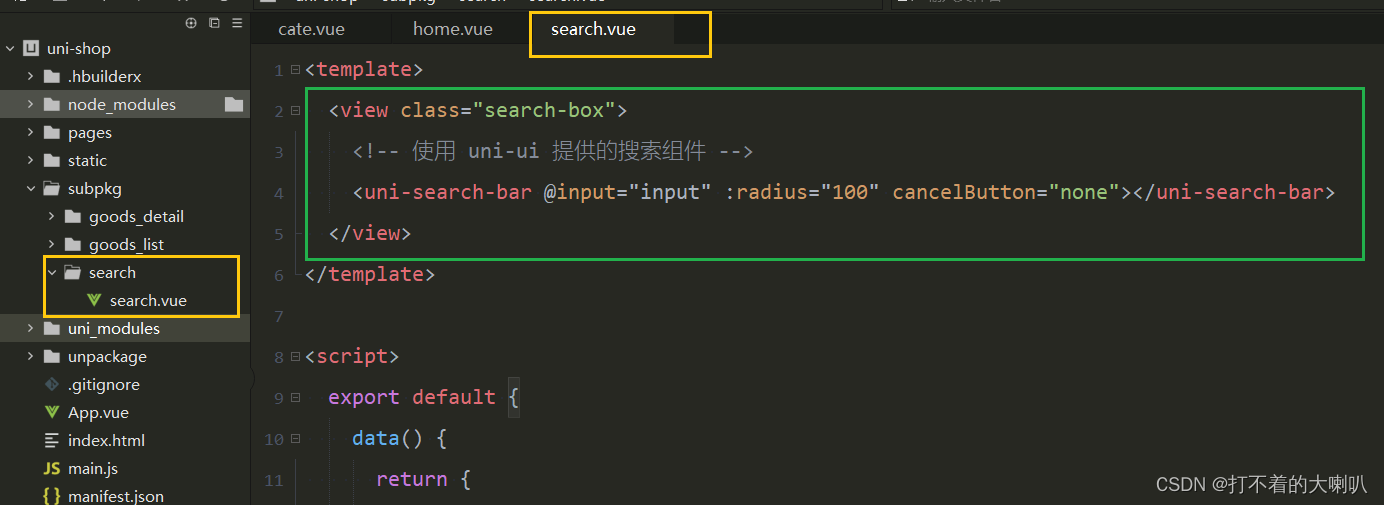
新版HBuilderX在uni_modules创建搜索search组件
1、创建自定义组件 my-search 新版HBuilder没有了 component 文件夹,但是有 uni_modules 文件夹,用来创建组件: 右键 uni_modules 文件夹,点击 新建uni_modules创建在弹出框,填写组件名字,例如:…...
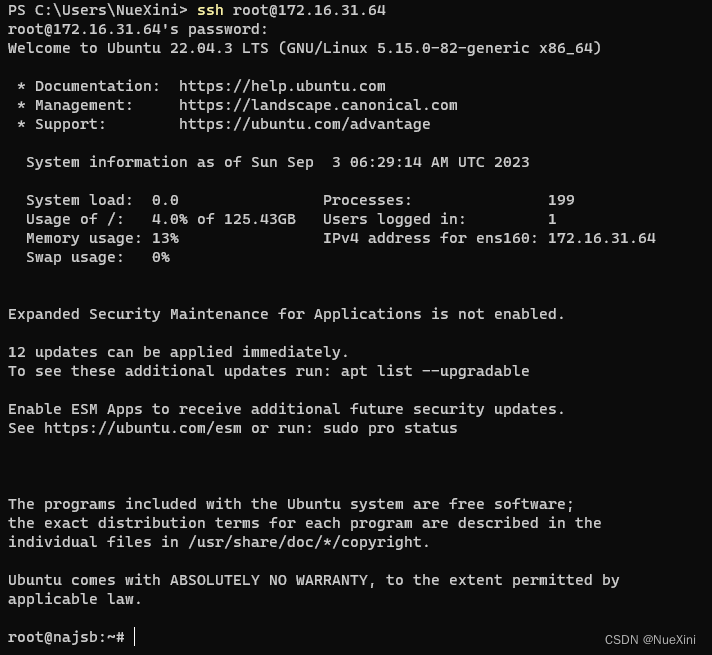
Ubutnu允许ssh连接使用root与密码登录
文章目录 1. 修改sshd_config2. 设置root密码3. 重启SSH服务 1. 修改sshd_config 修改/etc/ssh/sshd_config文件,找到 #Authentication,将 PermitRootLogin 参数修改为 yes。如果 PermitRootLogin 参数被注释,请去掉首行的注释符号ÿ…...
MySQL中表的设计
在MySQL中表的设计,需要一定的经验才能理解,由于笔者目前在读中,理解不是很深刻,仅根据自己的想法外界的一些参考资料做出下述文字描述,一些错误,请大佬及时指正~~ 在本篇文章中,介绍一点简单粗…...
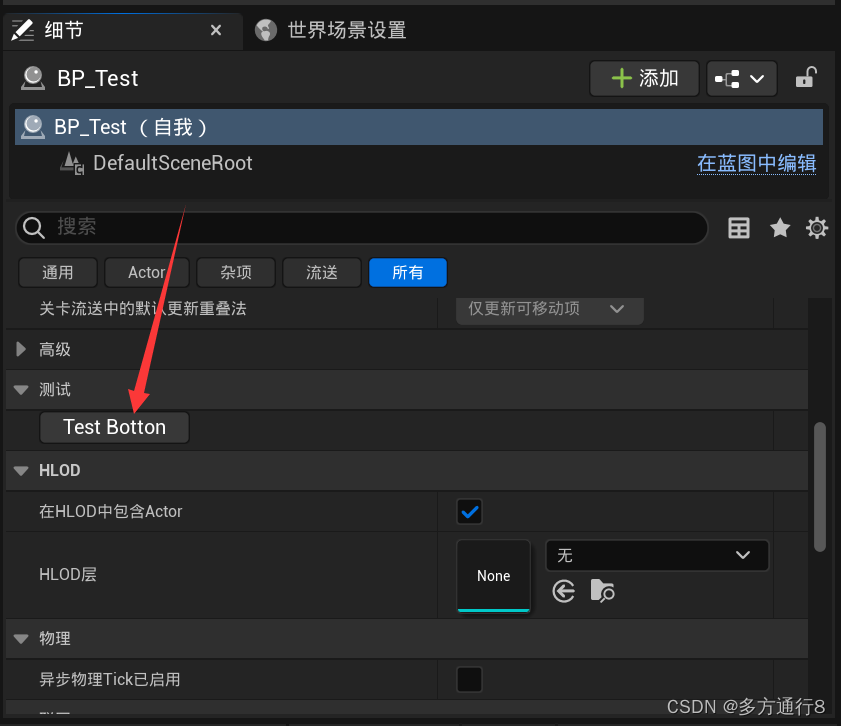
UE4/5在蓝图细节面板中添加函数按钮(蓝图与c++的方法)
目录 在细节面板中添加按钮使用函数 蓝图的方法 事件 函数 效果 uec的方法 效果 在细节面板中添加按钮使用函数 很多时候,我们可以看到一些插件的actor类中,点击一下之后就可以实现如矩阵一样的效果。 实际上是因为其使用了函数来修改了蓝图中的数…...

Python爬虫乱码问题之encoding和apparent_encoding的区别
encoding是从http中的header中的charset字段中提取的编码方式,若header中没有charset字段则默认为ISO-8859-1编码模式,则无法解析中文,这是乱码的原因 apparent_encoding会从网页的内容中分析网页编码的方式,所以apparent_encodi…...

Docker技术--Docker简介和架构
1.Docker简介 (1).引入 我们之前学习了EXSI,对于虚拟化技术有所了解,但是我们发现类似于EXSI这样比较传统的虚拟化技术是存在着一定的缺陷:所占用的资源比较多,简单的说,就是你需要给每一个用户提供一个操作平台,这一个…...
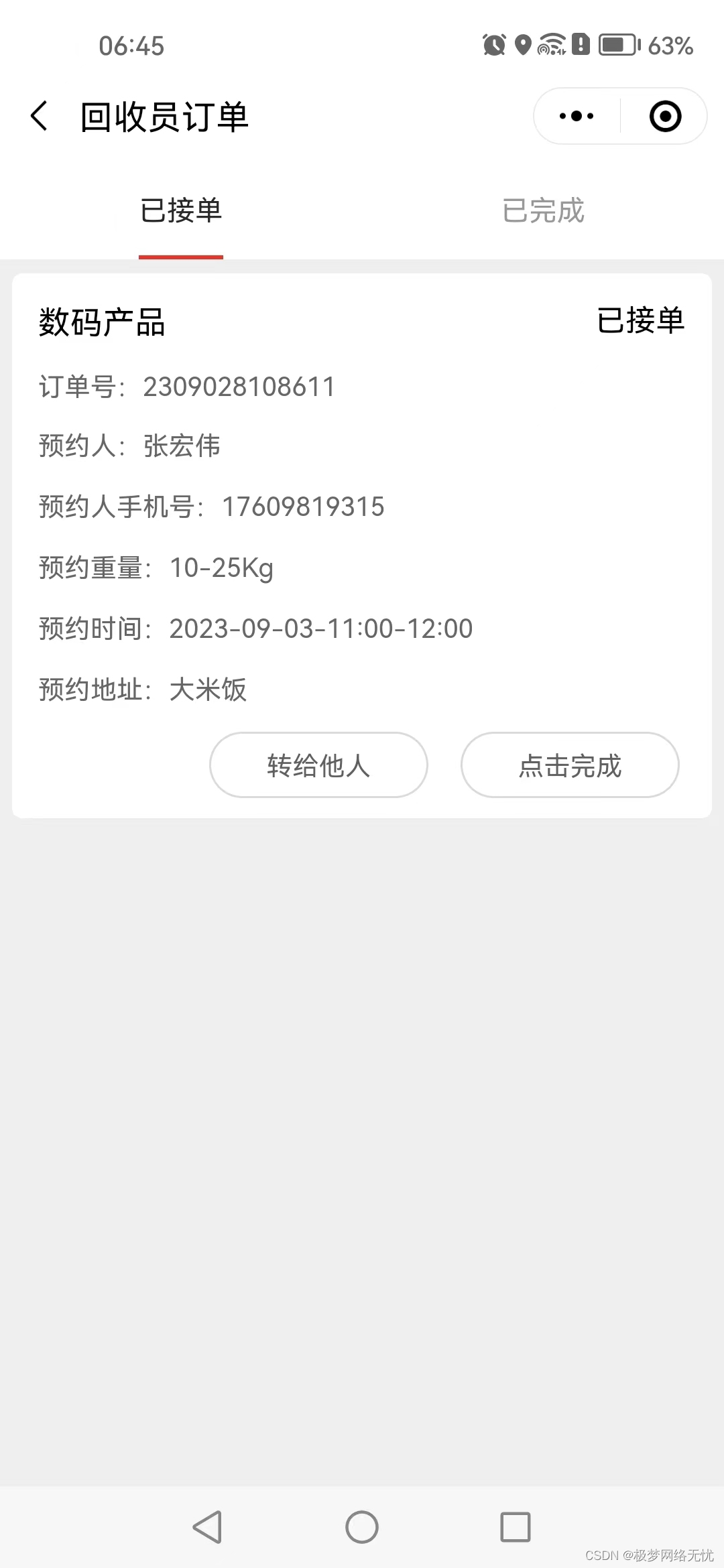
废品回收功能文档
废品回收 基础版 后台功能 功能字段描述二级分类表字段:图标、名称、描述、图片、注意事项、上一级、状态功能:前端展示和筛选;增删改查今日指导价表字段:关联分类、名称、价格、单位、状态功能:前端展示和预估价格&…...

【ARMv8 SIMD和浮点指令编程】NEON 乘法指令——asimdrdm
ARMv8 有许多版本(ARMv8.1 等),它们定义了强制和可选功能。Linux 内核通过 hwcaps 公开了其中一些功能的存在。这些值显示在 /proc/cpuinfo 中。 名称版本支持的特性fp-Single-precision and double-precision floating point.asimd-Advanced SIMD.evtstrmN/AGeneric timer …...
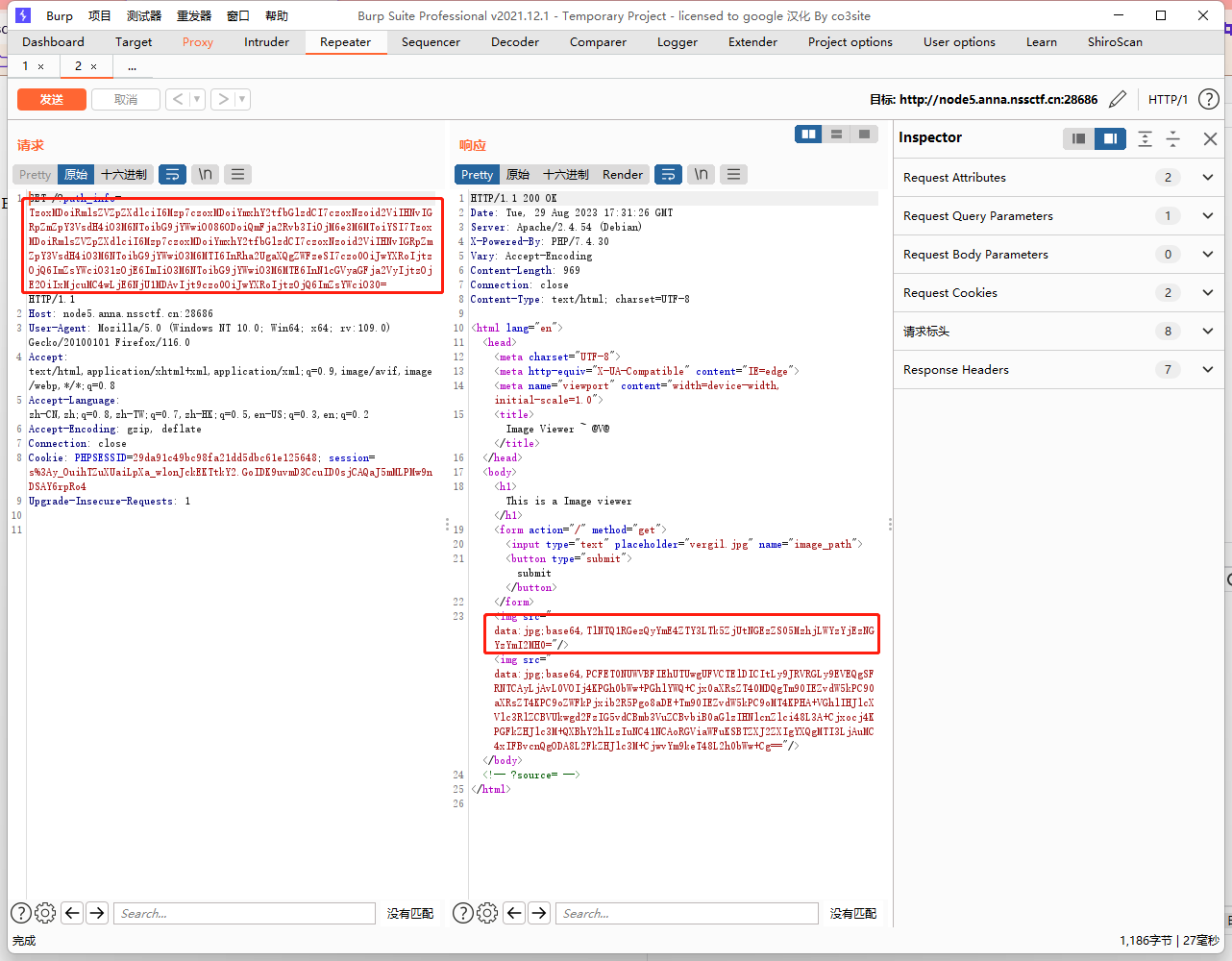
[SWPUCTF 2022]——Web方向 详细Writeup
SWPUCTF 2022 ez_ez_php 打开环境得到源码 <?php error_reporting(0); if (isset($_GET[file])) {if ( substr($_GET["file"], 0, 3) "php" ) {echo "Nice!!!";include($_GET["file"]);} else {echo "Hacker!!";} }e…...

Shell编程:流程控制与高级应用的深入解析
目录 Shell 流程控制 1、条件语句 2、循环语句 Shell 函数 Shell 输入/输出重定向 Shell 文件包含 文件包含的示例 Shell 流程控制 使用Shell编程时,流程控制是非常重要的,它允许你根据条件执行不同的命令或者控制程序的执行流程。Shell支持一些基…...
一文讲通嵌入式现状
近年来,随着计算机技术和集成电路技术的迅速发展,嵌入式技术在通讯、网络、工控、医疗、电子等领域日益普及,并发挥着越来越重要的作用。嵌入式系统已成为当前最为热门和前景广阔的IT应用领域之一。 随着信息化、智能化、网络化的不断推进&am…...

设计模式-代理模式Proxy
代理模式Proxy 代理模式 (Proxy)1) 静态代理1.a) 原理解析1.b) 使用场景1.c) 静态代理步骤总结 2) 动态代理2.a) 基于 JDK 的动态代理实现步骤2.b) 基于 CGLIB 的动态代理实现步骤2.c) Spring中aop的使用步骤 代理模式 (Proxy) 代理设计模式(Proxy Design Pattern&…...

如何使用CSS实现一个自适应等高布局?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 使用 Flexbox 布局⭐ 使用 Grid 布局⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发…...

Google colab部署VITS——零门槛快速克隆任意角色声音
目录 序言 查看GPU配置 复制代码库并安装运行环境 选择预训练模型 上传视频链接(单个不应长于20分钟) 自动处理所有上传的数据 训练质量相关:实验发现目前使用CJ模型勾选ADD_AUXILIARY,对于中/日均能训练出最好的效果&#x…...

14 | Spark SQL 的 DataFrame API 读取CSV 操作
sales.csv 内容 date,category,product,full_name,sales 2023-01-01,Electronics,Laptop,John Smith,1200.0 2023-01-02,Electronics,Smartphone,Jane Doe,800.0 2023-01-03,Books,Novel,Michael Johnson,15.0 2023-01-04,Electronics,Tablet,Emily Wilson,450.0 2023-01-05,B…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
