【密码学代码分享】突破ECDSA算法封装--JS无三方包纯手写ECDSA
ECDSA(Elliptic Curve Digital Signature Algorithm)是一种基于椭圆曲线密码学的数字签名算法。它用于确保数字数据的完整性和身份验证,通常在信息安全和加密通信中使用。在日常使用中,通常会使用一些函数库来实现完成这个算法的功能,但是有部分情况是需要自高度自定义ECDSA相关逻辑的,这里分享JavaScript语言在不借助第三方库的前提下纯手写的ECDSA算法代码,并对其实现原理进行解释。
文章目录
- 1.ECDSA算法原理
- 1.密钥生成算法
- 2.签名算法
- 3.验证算法
- 4.正确性证明
- 2.纯手写ECDSA 应用场景说明
- 3.JS实现的几大主要问题
- 1.大数运算
- 2.椭圆曲线群上的加法和乘法
- 4.完整代码(以secp256k1为例)
1.ECDSA算法原理
这里我直接copy之前自己文章中对其的详细描述。
ECDSA(Elliptic Curve Digital Signature Algorithm) 是使用椭圆曲线密码(ECC)对数字签名算法(DSA)的模拟。
ECDSA安全性依赖于基于椭圆曲线的有限群上的离散对数难题。与基于RSA的数字签名和基于有限域离散对数的数字签名相比,在相同的安全强度条件下,ECDSA方案具有如下特点:
- 签名长度短
- 密钥存储空间小
- 特别适用于存储空间有限、带宽受限、要求高速实现的场合(如在智能卡中应用)。
1.密钥生成算法
设 G F ( p ) GF(p) GF(p)为有限域, E E E是有限域上 G F ( p ) GF(p) GF(p)上的椭圆曲线。选择 E E E上一点 G ∈ E G\in E G∈E, G G G的阶为满足安全要求的素数 n n n,即 n G = O nG=O nG=O( O O O为无穷远点)。选择一个随机数 d d d, d ∈ [ 1 , n − 1 ] d \in [1, n-1] d∈[1,n−1],计算 Q Q Q,使得 Q = d G Q=dG Q=dG,那么公钥为 ( n , Q ) (n, Q) (n,Q),私钥为 ( d ) (d) (d)。
2.签名算法
签名者 A l i c e Alice Alice对消息 m m m签名的过程如下:
- (1)随机选取整数 k k k, k ∈ [ 1 , n − 1 ] k \in [1,n-1] k∈[1,n−1],计算 k G = ( x , y ) kG=(x,y) kG=(x,y), r ≡ x ( m o d n ) r \equiv x(mod \ n) r≡x(mod n);
- (2)计算 e = h ( m ) e=h(m) e=h(m), h h h为安全的散列函数;
- (3)计算 s ≡ ( e + r d ) k − 1 ( m o d n ) s \equiv (e+rd)k^{-1}(mod \ n) s≡(e+rd)k−1(mod n)。如果 r = 0 r=0 r=0或 s = 0 s=0 s=0,则令选取随机数 k k k,重新执行上面的过程。消息 m m m的签名为 ( r , s ) (r,s) (r,s)。
3.验证算法
签名接收者 B o b Bob Bob对消息 m m m签名 ( r , s ) (r,s) (r,s)的验证过程如下:
- (1)计算 e = h ( m ) e=h(m) e=h(m);
- (2)计算 u ≡ s − 1 e ( m o d n ) u \equiv s^{-1}e(mod \ n) u≡s−1e(mod n), v ≡ s − 1 r ( m o d n ) v \equiv s^{-1}r(mod \ n) v≡s−1r(mod n), ( x 1 , y 1 ) = u G + v Q (x_{1}, y_{1})=uG+vQ (x1,y1)=uG+vQ, r 1 ≡ x 1 ( m o d n ) r_{1} \equiv x_{1}(mod \ n) r1≡x1(mod n);
- (3)若 r = r 1 r=r_{1} r=r1,则签名有效;否则,签名无效。
4.正确性证明
由于
Q = d G s ≡ ( e + r d ) k − 1 ( m o d n ) k G = ( x , y ) u ≡ s − 1 e ( m o d n ) v ≡ s − 1 r ( m o d n ) ( x 1 , y 1 ) = u G + v Q Q=dG\\ s \equiv (e+rd)k^{-1}(mod \ n)\\ kG=(x,y)\\ u \equiv s^{-1}e(mod \ n)\\ v \equiv s^{-1}r(mod \ n)\\ (x_{1},y_{1})=uG+vQ Q=dGs≡(e+rd)k−1(mod n)kG=(x,y)u≡s−1e(mod n)v≡s−1r(mod n)(x1,y1)=uG+vQ
则有:
k ≡ ( e + r d ) s − 1 ≡ s − 1 e + s − 1 ≡ u + v d ( m o d n ) ( x , y ) = k G = u G + v d G = u G + v Q = ( x 1 , y 1 ) r 1 = x 1 m o d n = x m o d n = r k \equiv (e+rd)s^{-1} \equiv s^{-1}e+s^{-1} \equiv u+vd (\ mod \ n)\\ (x,y)=kG=uG+vdG=uG+vQ=(x_{1},y_{1})\\ r_{1}=x_{1} \ mod \ n = x \ mod \ n=r k≡(e+rd)s−1≡s−1e+s−1≡u+vd( mod n)(x,y)=kG=uG+vdG=uG+vQ=(x1,y1)r1=x1 mod n=x mod n=r
2.纯手写ECDSA 应用场景说明
从头开始手写的ECDSA算法毫无疑问在算法的效率上以及拓展性上要比封装好的函数库低不少,那么为什么还需要自己纯手写实现ECDSA的逻辑呢?如果存在以下需求,从头手写是一个好的选择。
- 1.如果需要对算法的逻辑进行高度的定制,常见的函数库提供的拓展功能都无法满足需求。例如需要高度定义其随机数的产生(部分函数库提供对随机数函数的拓展,但是拓展能力有限)、需要取到中间变量做一些其他的操作。
- 2.想在客户端隐蔽的使用ECDSA算法,不想直接使用三方包(这样特征太明显)。从攻击的角度来看,对着一个经过混淆后纯手写的ECDSA算法代码,如果不是对算法特别熟悉,分析难度还是不小的。
当你想使用自己手写的ECDSA的时候,就必须接受不能将其作为一个广泛应用、高频调用的算法包,因为算法的效率会差不少。
3.JS实现的几大主要问题
我们回顾下上面算法的细节,发现在JavaScript中实现,主要有两个方面的问题需要解决:
- 1.大数运算如何实现。
- 2.如何做椭圆曲线群上的加法和乘法操作。
1.大数运算
对于第一个问题,自从ECMAScript 2020(ES11)引入BigInt类型以来,JavaScript原生支持大整数运算。BigInt类型用于表示任意精度的整数,可以执行标准的算术操作。不需要额外的库,但在一些老版本的浏览器中可能不受支持。
2.椭圆曲线群上的加法和乘法
对于第二个问题,我们尝试推导下。
首先明确,椭圆曲线上加法的定义,假设有一根椭圆曲线 E : y 2 = x 3 + a x + b E: y^2=x^3+ax+b E:y2=x3+ax+b,其中, a a a 和 b b b 是曲线的参数, x x x 和 y y y 是曲线上的点坐标。在椭圆曲线上的加法操作定义如下:
- 点加法:给定曲线上的两个点 P P P和 Q Q Q,点加法操作 P + Q P+Q P+Q的结果是曲线上另一个点 R R R。
- 加法规则:
- 如果 P P P和 Q Q Q是相同的点,那么点加法操作是对 P P P的倍乘,即 P + P P+P P+P。
- 如果 P P P和 Q Q Q是不同的点,并且它们不是垂直于 x 轴的,那么点加法操作的步骤是:连接 P P P和 Q Q Q,计算直线 L L L,找到直线与曲线 E E E的交点 R R R, R R R关于x轴的对称点 − R -R −R就是 P + Q P+Q P+Q的结果。
- 特殊情况:在某些情况下,点加法操作可能会遇到特殊情况,例如 P P P 与 Q Q Q 垂直于 x 轴,或 P P P 与 Q Q Q 是互为相反元素。这些情况需要根据具体的椭圆曲线参数和实现进行处理。
从上可以看出,我们主要需要处理的情况就是找到两点所确定的直线和曲线的交点,对于这个交点,我们尝试建立方程进行解出。
设 P P P的坐标为 ( x 1 , y 1 ) (x_{1},y_{1}) (x1,y1), Q Q Q的坐标为 ( x 2 , y 2 ) (x_{2},y_{2}) (x2,y2),两点所确立的直线为: y − y 1 = k ( x − x 1 ) + b y-y_{1}=k(x-x_{1})+b y−y1=k(x−x1)+b, k = x 1 − x 2 y 1 − y 2 k= \frac{x_{1}-x{2}}{y_{1}-y_{2}} k=y1−y2x1−x2。
通过求导的方式计算出 E E E上某点的斜率:
F ( x ) = x 3 + a x + b − y 2 F x ′ = 3 x 2 + a F y ′ = − 2 y k = − F y ′ F x ′ = 3 x 2 + a 2 y F(x)=x^3+ax+b-y^2\\F_{x}'=3x^2+a\\F_{y}'=-2y\\k=-\frac{F_{y}'}{F_{x}'}=\frac{3x^2+a}{2y} F(x)=x3+ax+b−y2Fx′=3x2+aFy′=−2yk=−Fx′Fy′=2y3x2+a
联立上式子,可以解得直线 L L L与曲线 E E E的交点:
x 3 = k 2 − x 1 − x 2 y 3 = y 1 + k ( x 2 − x 1 ) x_{3}=k^2-x_{1}-x_{2}\\y_{3}=y_{1}+k(x_{2}-x_{1}) x3=k2−x1−x2y3=y1+k(x2−x1)
椭圆曲线上的乘法,只需采用快速幂的方式进行加法运算即可。
至此,用JS纯手写的两大核心问题都解决了,具体细节处理见代码。
4.完整代码(以secp256k1为例)
- 下面代码已经过完整测试并以用于具体生产项目中。
- 其中签名产生的v值为以太坊中相关约定,不需要可以去除。
- 签名值保证了s一定小于n的一半(以太坊相关约定),所以提取随机数的时候是会有两种可能。不需要该处逻辑可以去除。
// 椭圆曲线点定义
class Point{constructor(x,y){this.x = BigInt(x);this.y = BigInt(y);}
}
// secp256k1曲线
const secp_p = BigInt('0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F'); // 2n ** 256n - 2n ** 32n - 977n;
const secp_n = BigInt('0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141'); // 2n ** 256n - 432420386565659656852420866394968145599n;
const secp_a = BigInt(0);
const Gx = BigInt('0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798');
const Gy = BigInt('0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8');
const secp_G = new Point(Gx, Gy);function get_inv(x, y, p){return x === 1n ? 1n : get_inv(y % x, y, p) * (y - y / x) % p;
}// 求模逆元
function modInverse(b,p){return get_inv(b%p,p,p);
}// 最大公约数
function get_gcd(x,y){return y ? get_gcd(y,x%y):x;
}// 在有限域下计算的求模
function mod(a, b) {const result = a % b;return result >= 0n ? result : b + result;
}// 椭圆曲线点加法
function point_add(pa, pb, p){// 零点相加if(pa.x === 0n && pa.y === 0n || pb.x === 0n && pb.y === 0n){return new Point(pa.x+pb.x, pa.y+pb.y);}// 对称点相加if(pa.x === pb.x && pa.y !== pb.y){return new Point(0, 0);}// 定义斜率k的分母和分子let k, k_num, k_den;// k的分子分母计算if(pa.x === pb.x && pa.y === pb.y){// 自己和自己相加 斜率为该点切线k_num = 3n * pa.x * pa.x + secp_a;k_den = 2n * pa.y;} else {// 两点确定斜率k_num = pa.y - pb.y;k_den = pa.x - pb.x;}// k符号记载let neg = 0;if(k_num * k_den < 0n){neg = 1;k_num = k_num > 0n ? k_num : -k_num;k_den = k_den > 0n ? k_den : -k_den;}// k化简分子分母let gcd = get_gcd(k_num, k_den);k_num /= gcd;k_den /= gcd;// 分母不为1,计算逆元if(k_den !== 1n){k_den = modInverse(k_den, p);}k = k_num * k_den % p;if(neg === 1) {k = -k;}// 计算最终结果let x3 = mod(k * k - pa.x - pb.x, p);let y3 = mod(k * (pa.x - x3) - pa.y, p);return new Point(x3, y3);
}// 椭圆曲线点快速乘法
function point_mul(n, g, p){n = BigInt(n)let ans = new Point(0, 0);while(n > 0n){if(n & 1n){ans = point_add(ans, g, p);}g = point_add(g, g, p);n >>= 1n;}return ans;
}export default {// 由私钥生成公钥generatePublicKey(privateKey) {// 私钥类型校验if(typeof privateKey != 'bigint') {throw new Error("私钥不是BigInt类型");}const publicKey = point_mul(privateKey, secp_G, secp_p);return publicKey;},ecSign(privateKey, msgHash, k) {// k类型校验if(typeof k != 'bigint') {throw new Error("随机数k不是BigInt类型");}// k大小校验if(k < 1n || k > secp_n - 1n) {throw new Error("随机数k不符合要求");}// 私钥类型校验if(typeof privateKey != 'bigint') {throw new Error("私钥不是BigInt类型");}// msg校验// if(typeof msg != 'string') {// throw new Error("msg不是string类型");// }const d = privateKey;//const e = keccak256Int(msg);const e = BigInt("0x" + msgHash);const kG = point_mul(k, secp_G, secp_p);const r = kG.x;var s = modInverse(k, secp_n) * (e + r * d) % secp_n;if(r === 0n || s === 0n) {throw new Error("随机数k不符合要求");}const v = (kG.y % 2n) ^ (s * 2n < secp_n ? 0n : 1n);if(s * 2n >= secp_n) {s = secp_n - s;}return [r, s, v];},ecVerify(publicKey, msgHash, sign) {// msg校验// if(typeof msg != 'string') {// throw new Error("msg不是string类型");// }const r = sign[0];const s = sign[1];const Q = publicKey;//const e = keccak256Int(msg);const e = BigInt("0x" + msgHash);const s_inv = modInverse(s, secp_n);const u = s_inv * e % secp_n;const v = s_inv * r % secp_n;const uG = point_mul(u, secp_G, secp_p);const vQ = point_mul(v, Q, secp_p);const uG_add_vQ = point_add(uG, vQ, secp_p);const r1 = uG_add_vQ.x;return r === r1;},// 提取ECDSA随机数 s有两个可能,会产生两个可能的k// privateKey msgHash 都是bigint sign = [r, s]extractRandomK(privateKey, msgHash, sign) {// 私钥类型校验if(typeof privateKey != 'bigint') {throw new Error("私钥不是BigInt类型");}// msg校验// if(typeof msg != 'string') {// throw new Error("msg不是string类型");// }function recoverK(s) {const d = privateKey;const r = sign[0];//const s = secp_n - sign[1];//const e = keccak256Int(msg);const e = BigInt("0x" + msgHash);const s_inv = modInverse(s, secp_n);const k = s_inv * (e + r * d) % secp_n;return k;}return [recoverK(sign[1]), recoverK(secp_n - sign[1])];},
}ATFWUS 2023-09-02
相关文章:

【密码学代码分享】突破ECDSA算法封装--JS无三方包纯手写ECDSA
ECDSA(Elliptic Curve Digital Signature Algorithm)是一种基于椭圆曲线密码学的数字签名算法。它用于确保数字数据的完整性和身份验证,通常在信息安全和加密通信中使用。在日常使用中,通常会使用一些函数库来实现完成这个算法的功…...

stable diffusion实践操作-文生图
本文专门开一节写文生图相关的内容,在看之前,可以同步关注: stable diffusion实践操作 正文 1 liblib SD1.5底模 lora(baihuaniang_1.0) 详细信息: 底模:SD 1.5 Lora:baihuaniang_1.0 正向提示词: Best …...
Spring容器及实例化
一、前言 Spring 容器是 Spring 框架的核心部分,它负责管理和组织应用程序中的对象(Bean)。Spring 容器负责创建、配置和组装这些对象,并且可以在需要时将它们提供给应用程序的其他部分。 Spring 容器提供了两种主要类型的容器&…...

# Go学习-Day9
文章目录 Channel声明存入取出一个简单的死锁分析 个人博客:CSDN博客 Channel Channel本质是一个队列多goroutine访问时不需要加锁,Channel天然线程安全channel有类型,只能写入相同类型channel是引用类型channel必须初始化才能写入数据&…...

chatGPT如何在Java中使用
ChatGPT是一个基于GPT模型的聊天机器人平台,它提供了API接口,可以通过HTTP请求与之交互。您可以使用Java编写程序,通过HTTP请求与ChatGPT进行交互,实现聊天机器人的功能。 具体步骤如下: 1、注册ChatGPT账号并创建应…...
——基础积累)
vue+axios——创建多个实例共用请求拦截器和响应拦截器(403错误信息不提示bug解决)——基础积累
创建多个实例共用请求拦截器和响应拦截器:使用的是函数的继承,也就是call()方法,这个方法第一个参数就是this,后面的参数可以是一个也可以是多个。最后一定要记得要return出去,否则接口是拿不到数据的。 import axios from axios…...
全球免费编程教育网站:Code.org
全球免费编程教育网站:Code.org 官网地址注册使用 你还在为小朋友的编程教育而发愁吗? 你还在为小朋友放假无聊而头疼吗? 他来了他来了,全球免费编程教育网站来了。 2013年成立的Code.org是一个非营利组织。 它致力于为年轻女子、…...
构造函数与成员变量初始化
C自学精简教程 目录(必读) 1 为什么需要定义构造函数? 构造函数主要用来给成员变量初始化。 让类对象有一个良好的开始状态。 2 构造函数初始化成员变量 下面我们来完善上一篇文章中的几个构造函数。 让这些构造函数完成给成员变量初始化的职责。 为此&#…...

使用Go env命令设置Go的环境
文章目录 前言Linux的设置Windlows设置Go version > 1.13 当你的GO的版本大于1.13的时候 Set environment variable allow bypassing the proxy for selected modules 前言 在进行Go开发的时候,设置Go的环境变量信息是必须的。下面介绍windows和Linux࿰…...
)
目标检测YOLO实战应用案例100讲-道路场景下目标检测与分割模型的压缩研究与实现(续)
目录 道路场景下目标检测与语义分割模型的改进研究 3.1 道路场景数据集分析 3.1.1 Cityscapes数据集...
b站手机缓存文件转MP4
b站缓存的文件 音频、视频、弹幕是分开的 这里我只用到了音频和视频所以只介绍这一部分 b站的缓存视频文件和路径结构如下 默认缓存路径 内部存储\Android\data\tv.danmaku.bilil\download\89720189 文件夹结构 文件夹 c_738583 这是单个视频的缓存文件夹 进入c_738583文件夹…...
一个集成的BurpSuite漏洞探测插件1.2
4、DNSLog查询漏报 注:扫描结束后才会在BurpSuite的Target、Dashboard模块显示高危漏洞,进程扫描中无法进行同步,但可以在插件中查看(涉及到DoPassive方法问题)。...

[FMMPEG] parse与 demuxer
FFmpeg源码分析:av_parser_parse2()解析数据包 ffmpeg 4.3添加自定义demuxer ffmpeg API基础...

【Bug】Ubuntu 有线设置打不开无反应
前言: 突然有线设置就没法启用了,但是能联网,能查看ip 解决: 最后安装了一个新的依赖包: sudo apt install gnome-control-center 然后就可以了 还有一个方法,没试过,但感觉有点道理的&#…...

迈向无限可能, ATEN宏正领跑设备切换行业革命!
随着互联网在各个领域的广泛应用,线上办公这一不受时间和地点制约、不受发展空间限制的办公模式开始广受追捧,预示着经济的发展正朝着新潮与活跃的方向不断跃进。当然,在互联网时代的背景下,多线程、多设备的线上办公模式也催生了许多问题:多设备间无法进行高速传输、切换;为保…...

Ubuntu18.04:ORB-SLAM3使用数据集构建地图和保存点云地图
文章目录 保存地图方法一:使用ORB-SLAM3自带的保存方法(oea后缀文件)保存地图方法二:使用PCL库保存为PCD类型地图文件安装PCL库:取巧方法:CMakeLists.txt 文件修改内容:(向该文件内添…...
找到自制电子杂志的方法了,快来看看?
终于找到自制电子杂志的方法了,这真是令人兴奋啊!现在,我们可以利用这个方法来创造属于自己的电子杂志,将我们的想法和创意以独特的方式展现给世界。 1.需要一个电子杂志制作工具 市面上有许多专门用于制作电子杂志的工具&#x…...
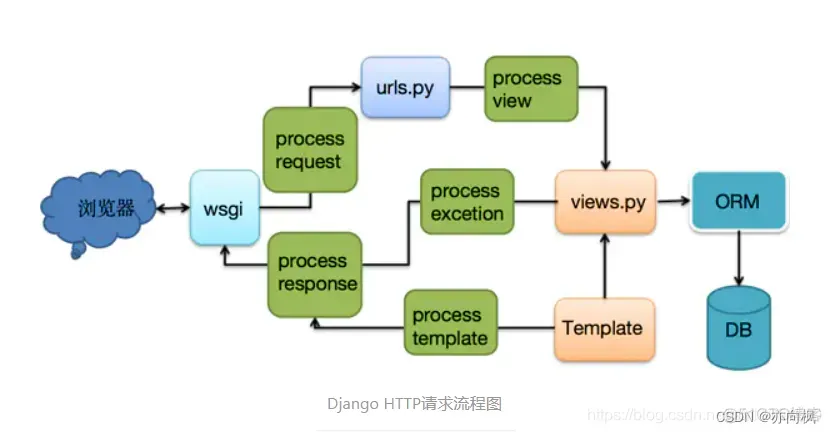
Django请求的生命周期
Django请求的生命周期是指: 当用户在浏览器上输入URL到用户看到网页的这个时间段内,Django后台所发生的事情。 直白的来说就是当请求来的时候和请求走的阶段中,Django的执行轨迹。 一个完整的Django生命周期: 用户从客户端发出一条请求以后ÿ…...

Kotlin 中 OkHttp 使用及解析
build.gradle dependencies {//OkHttpimplementation com.squareup.okhttp3:okhttp:4.9.0 } 简单使用例子 val okHttpClient OkHttpClient.Builder().connectTimeout(Duration.ofSeconds(10)).readTimeout(Duration.ofSeconds(10)).writeTimeout(Duration.ofSeconds(10)).re…...
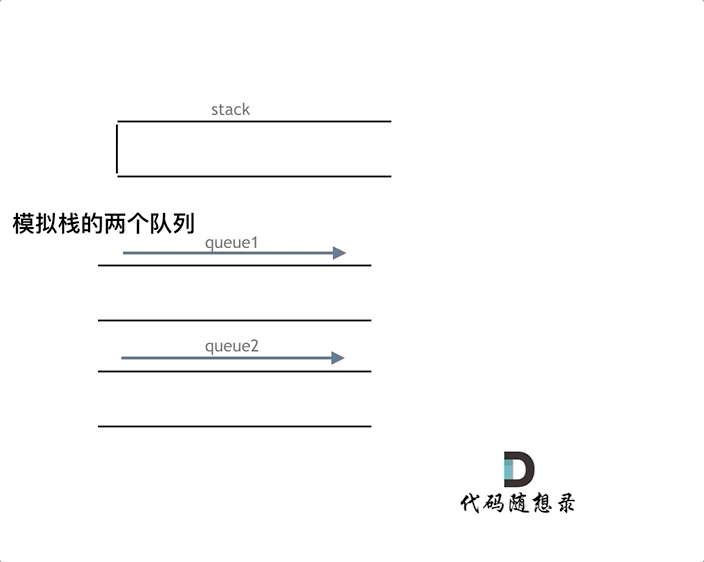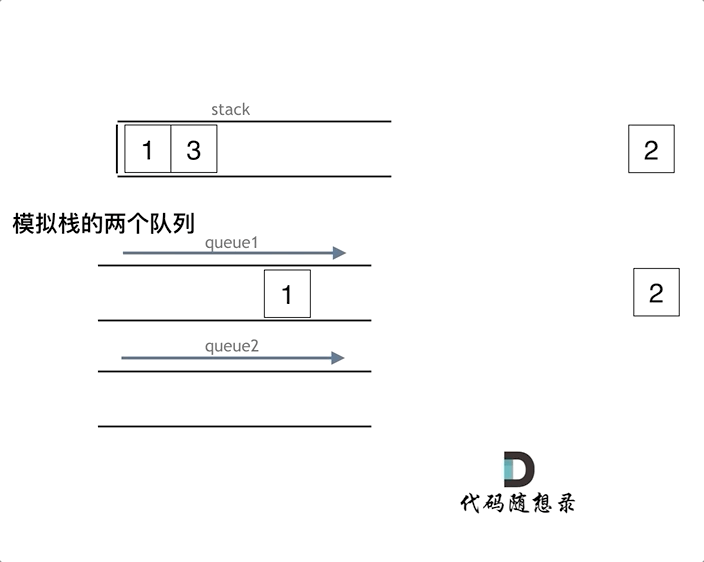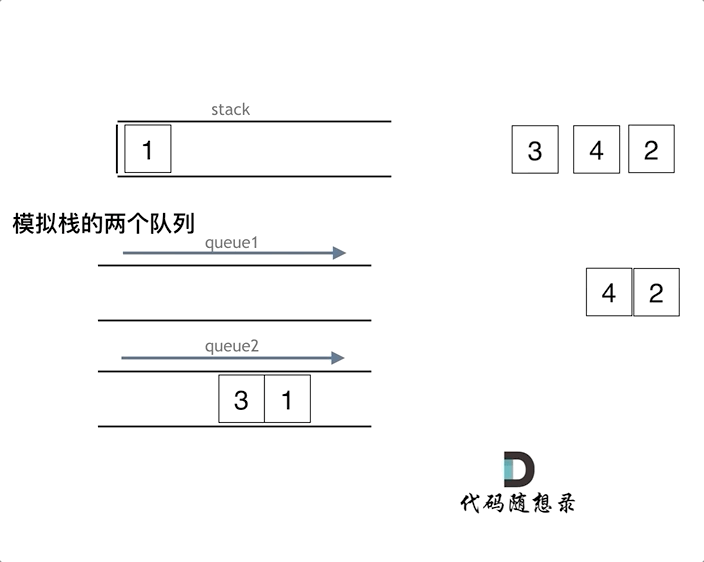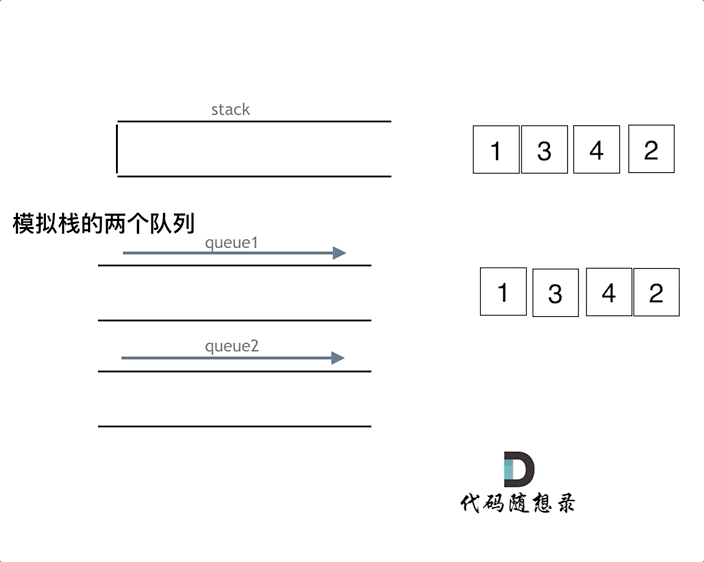
【C++代码】用栈实现队列,用队列实现栈--代码随想录
队列是先进先出,栈是先进后出。卡哥给了关于C方向关于栈和队列的4个问题: C中stack 是容器么? 使用的stack是属于哪个版本的STL? 使用的STL中stack是如何实现的? stack 提供迭代器来遍历stack空间么? …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
