迭代器模式简介
概念:
迭代器模式是一种行为型设计模式,它提供了一种访问集合对象元素的方法,而无需暴露其内部表示。通过使用迭代器,可以按照特定顺序遍历集合中的元素。
特点:
- 将遍历和具体集合分离,使得能够独立地改变集合的实现方式。
- 提供了一个统一的接口来访问不同类型的集合对象。
- 隐藏了对于底层数据结构和算法的细节。
优点:
- 简化了客户端代码,将遍历逻辑从业务逻辑中解耦出来。
- 提供了对不同类型集合对象进行统一操作的能力。
- 支持多种遍历方式。
缺点:
- 对于某些复杂数据结构或算法可能需要自定义迭代器实现,增加了开发成本和复杂性。
- 在某些情况下可能会导致额外内存消耗。
适用场景:
- 当需要以相同方式遍历不同类型(如数组、链表、树等)的集合对象时可以使用迭代器模式。
- 当希望隐藏底层数据结构并提供一个统一接口来访问元素时可以使用迭代器模式。
实现方式:
内部迭代器:
在集合对象内部定义一个迭代器类,由集合对象主动调用迭代器的方法进行遍历。
实现原理:
- 集合类中包含一个迭代器类并实现含获取迭代器的方法。
- 迭代器类实现一个接口或抽象类,其中包含判断是否有下一个元素和获取下一个元素的方法。
- 在具体集合类中定义一个私有内部类作为具体的迭代器实现,并在该内部类中实现相关方法。
实现代码:
// 这里假设我们有一个名为MyCollection的具体集合类import java.util.ArrayList;
import java.util.List;class MyCollection<T> {private List<T> elements;public MyCollection() {this.elements = new ArrayList<>();}public void add(T element) {elements.add(element);}// 获取内部迭代器public Iterator<T> getIterator() {return new ConcreteIterator();}// 具体迭代器类,实现了Iterator接口private class ConcreteIterator implements Iterator<T> {private int index;@Overridepublic boolean hasNext() {return index < elements.size();}@Overridepublic T next() {if (this.hasNext()) {return elements.get(index++);}return null;}}
}// 定义一个迭代器接口
interface Iterator<T> {boolean hasNext();T next();
}public class Main {public static void main(String[] args) {
// 使用示例MyCollection<String> collection = new MyCollection<>();collection.add("A");collection.add("B");collection.add("C");// 获取内部迭代器并遍历集合元素Iterator<String> iterator = collection.getIterator();while (iterator.hasNext()) {String element = iterator.next();System.out.println(element);}}
}
在上述示例中,我们创建了一个具体集合类 MyCollection ,其中包含一个私有内部类 ConcreteIterator 实现了迭代器接口。
在具体集合类中定义的 getIterator() 方法返回该内部迭代器对象。客户端代码可以通过调用该方法获取到具体集合的内部迭代器,并使用循环遍历输出每个元素。在实际应用中,还可以根据需要对内部迭代器进行扩展,例如添加过滤条件、排序等操作。
存在的问题:
- 内部迭代器无法同时处理多个不同类型的集合对象。
- 内部迭代器无法灵活地改变遍历顺序或跳过特定元素。
- 集合对象对于每个元素都要进行完整遍历操作,如果只需要访问某些特定元素可能会造成性能损失。
外部迭代器:
客户端代码通过调用外部的迭代器来遍历集合对象。在外部迭代器中,客户端代码通过手动调用迭代器的方法来遍历集合对象,并可以灵活地控制遍历顺序和跳过特定元素。
实现原理:
- 在具体集合类中提供一个返回该迭代器对象的方法。
- 迭代器可以是自己创建的也可以使用java内置的迭代器。
- 在客户端代码中手动调用迭代器的方法进行遍历操作。
实现代码:
// 这里假设我们有一个名为MyCollection的具体集合类import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;class MyCollection<T> {private List<T> elements;public MyCollection() {this.elements = new ArrayList<>();}public void add(T element) {elements.add(element);}// 获取内部迭代器public Iterator<T> getIterator() {return elements.iterator();}
}public class Main {public static void main(String[] args) {
// 使用示例MyCollection<String> collection = new MyCollection<>();collection.add("A");collection.add("B");collection.add("C");// 获取外部迭代器并遍历集合元素Iterator<String> iterator = collection.getIterator();while (iterator.hasNext()) {String element = iterator.next();System.out.println(element);}}
}
在上述示例中,我们创建了一个具体集合类 MyCollection ,其中的 getIterator() 方法返回了Java内置的迭代器对象。
在客户端代码中,我们通过调用具体集合的 getIterator() 方法获取到外部迭代器,并使用循环遍历输出每个元素。在实际应用中,可以根据需要使用不同类型的外部迭代器,例如自定义实现一个针对特定需求进行封装的外部迭代器类。这样可以灵活地控制遍历逻辑和提供额外功能。
相关文章:

迭代器模式简介
概念: 迭代器模式是一种行为型设计模式,它提供了一种访问集合对象元素的方法,而无需暴露其内部表示。通过使用迭代器,可以按照特定顺序遍历集合中的元素。 特点: 将遍历和具体集合分离,使得能够独立地改…...

四方定理c++题解
题目描述 四方定理是数论中著名的一个定理,指任意一个自然数都可以拆成四个自然数的平方之和。例如: 251^22^22^24^2 对 25来说,还有其他方案: 250^20^23^24^2 以及 250^20^20^25^2 给定一个自然数 n ,请输出 n…...
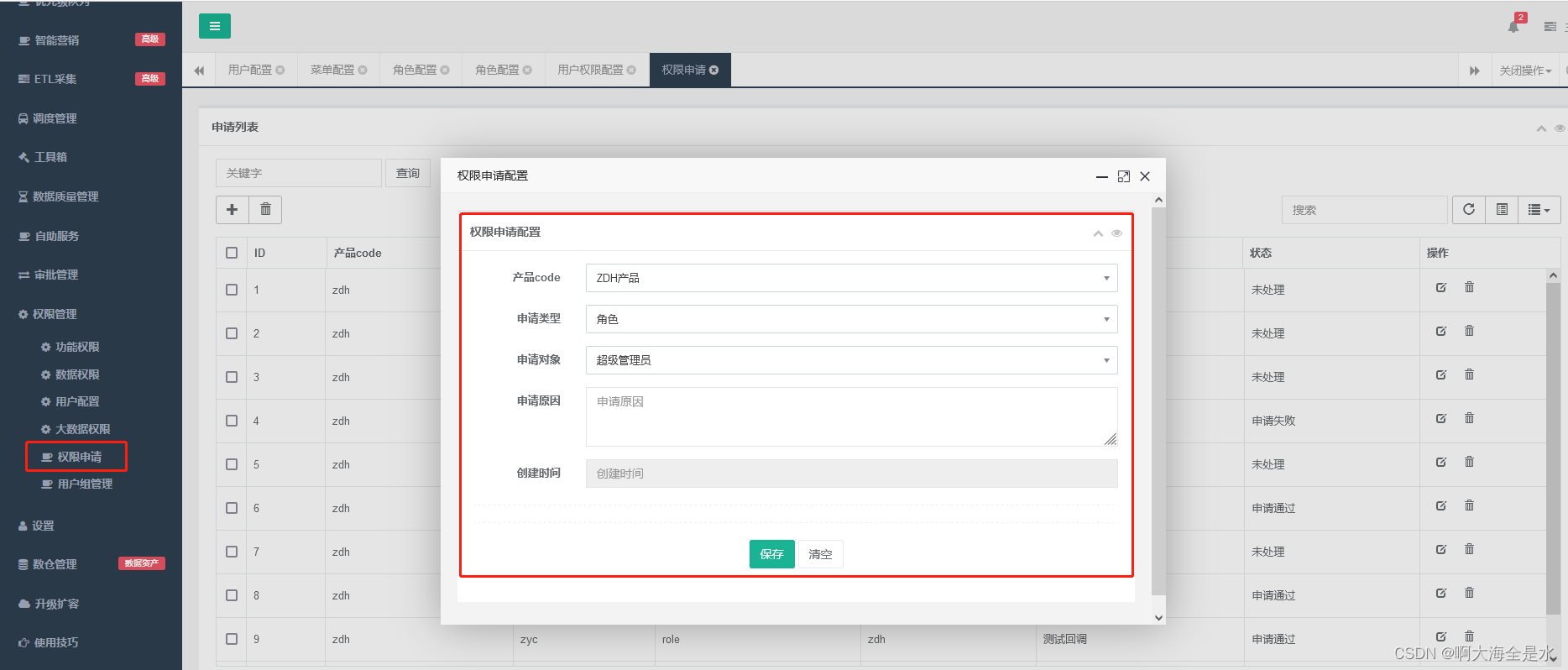
ZDH-权限模块
本次介绍基于ZDH v5.1.2版本 目录 项目源码 预览地址 安装包下载地址 ZDH权限模块 ZDH权限模块-重要名词划分 ZDH权限模块-菜单管理 ZDH权限模块-角色管理 ZDH权限模块-用户配置 ZDH权限模块-权限申请 项目源码 zdh_web: GitHub - zhaoyachao/zdh_web: 大数据采集,抽…...
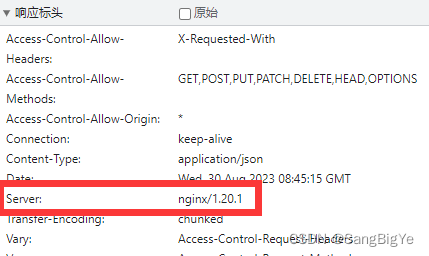
漏洞修复:在应用程序中发现不必要的 Http 响应头
描述 blablabla描述,一般是在返回的响应表头中出现了Server键值对,那我们要做的就是移除它,解决方案中提供了nginx的解决方案 解决方案 第一种解决方案 当前解决方案会隐藏nginx的版本号,但还是会返回nginx字样,如…...

什么是mkp勒索病毒,中了mkp勒索病毒怎么办?勒索病毒解密数据恢复
mkp勒索病毒是一种新兴的计算机木马病毒,它以加密文件的方式进行勒索,对用户的计算机安全造成了严重威胁。本文将介绍mkp勒索病毒的特征、影响以及应对措施,以便读者更好地了解和防范这种病毒。 一、mkp勒索病毒的特征 加密文件:…...

db2迁移至oracle
1.思路 (1)用java连接数据库(2)把DB2数据导出为通用的格式如csv,json等(3)导入其他数据库,比如oracle,mongodb。这个方法自由发挥的空间比较大。朋友说他会用springboot…...

webpack学习使用
...

按钮控件之2---QComboBox 复选按钮/复选框控件
1、常用函数: comboBox->addItem("cxq"); //添加下拉选项 combobox->clear(); //清空下拉项comboBox->setCurrentIndex(0);//设置当前的索引 int currentlndex(): //返回当前项的序号,第一个项的序号…...
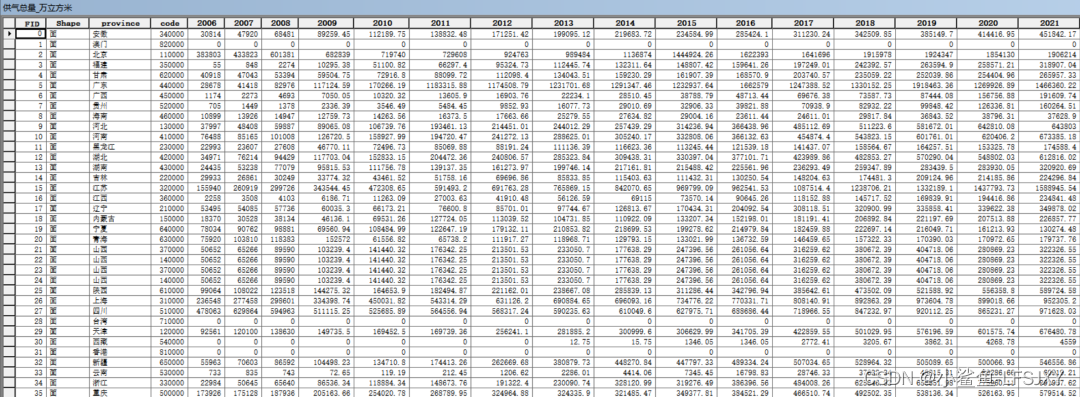
【数据分享】2006-2021年我国省份级别的燃气相关指标(免费获取\20多项指标)
《中国城市建设统计年鉴》中细致地统计了我国城市市政公用设施建设与发展情况,在之前的文章中,我们分享过基于2006-2021年《中国城市建设统计年鉴》整理的2006—2021年我国省份级别的市政设施水平相关指标、2006-2021年我国省份级别的各类建设用地面积数…...
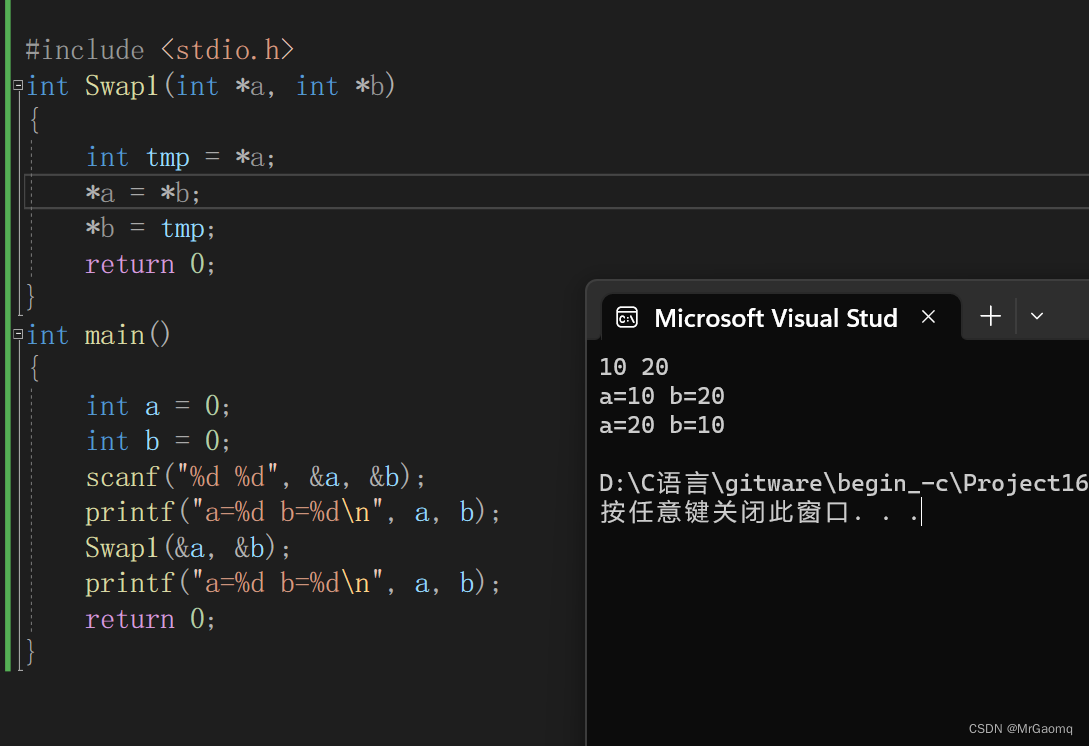
C语言深入理解指针(非常详细)(二)
目录 指针运算指针-整数指针-指针指针的关系运算 野指针野指针成因指针未初始化指针越界访问指针指向的空间释放 如何规避野指针指针初始化注意指针越界指针不使用时就用NULL避免返回局部变量的地址 assert断言指针的使用和传址调用传址调用例子(strlen函数的实现&a…...

Web3j 继承StaticStruct的类所有属性必须为Public <DynamicArray<StaticStruct>>
Web3j 继承StaticStruct的类所有属性必须为Public,属性的顺序和数量必须和solidity 里面的struct 属性相同,否则属性少了或者多了的时候会出现错位 Web3j 继承StaticStruct的类所有属性不能为private,因为web3j 是通过长度去截取返回值解析成…...

Kubernetes(k8s)上安装Prometheus和Grafana监控
Kubernetes上安装Prometheus和Grafana监控 环境准备Kubernetes准备 安装项目开始安装下载安装的项目安装项目替换镜像替换kube-state-metrics替换prometheus-adapter 修改Service修改alertmanager-service.yaml修改grafana-service.yaml修改prometheus-service.yaml 执行这些ya…...

黑马 软件测试从0到1 常用分类 模型 流程 用例
课程内容: 1、软件测试基础 2、测试设计 3、缺陷管理 4、Web常用标签 5、项目实战 以终为始,由交付实战目标为终,推出所学知识;从认识软件及软件测试,到如何设计测试、缺陷标准及缺陷管理,最终以项目实战贯…...

面试中的商业思维:如何展示你对业务的理解
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
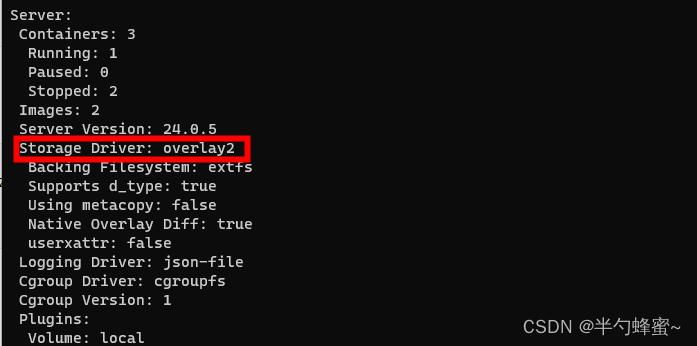
Docker切换文件系统为VFS
一、介绍 Docker支持AUFS、Btrfs、Device Mapper、OverlayFS、VFS、ZFS六种不同的存储驱动。 1. AUFS AUFS是一种常见的存储驱动程序,它也使用了Linux内核的AUFS文件系统。它的优点是支持所有的Linux发行版,可以在不同的容器之间共享文件系统…...
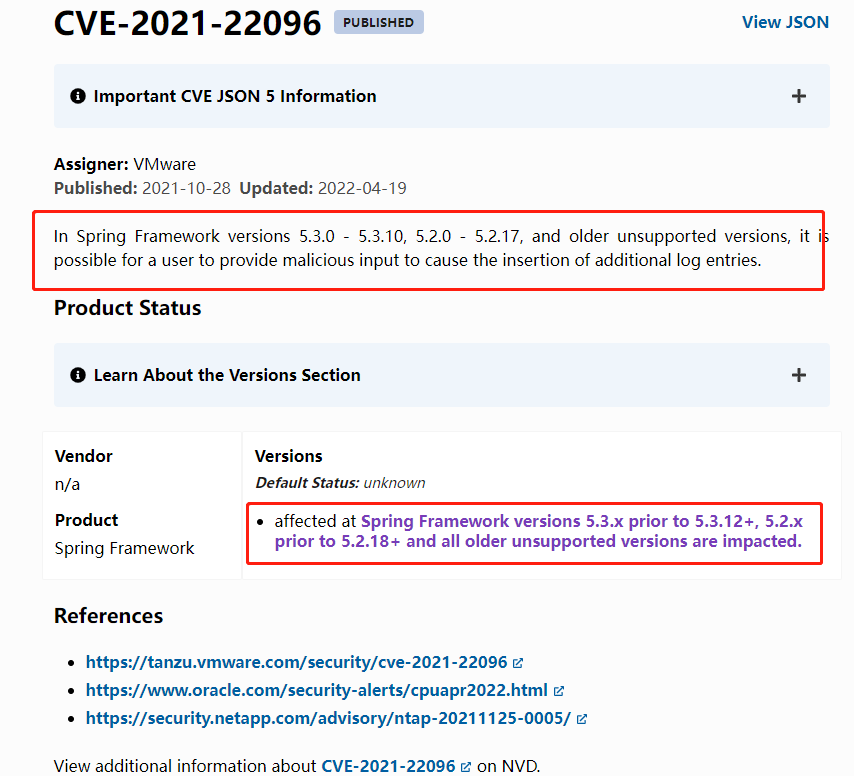
Spring Security存在认证绕过漏洞 CVE-2021-22096
文章目录 0.前言1.参考文档2.基础介绍漏洞影响范围:官方说明:修复版本:漏洞利用步骤:修复方式: 3.解决方案 0.前言 背景:项目被扫到Spring Boot 的漏洞,严格的说应该是Spring Security 组件的漏…...

前端list列表自定义图标并设置大小
前端list列表自定义图标并设置大小 一、前端list列表基础知识回顾 前端公有两种列表,一种是有序列表(ol),一种是无序列表(ul),它们的子元素都是(li)。 1.1 有序列表&a…...
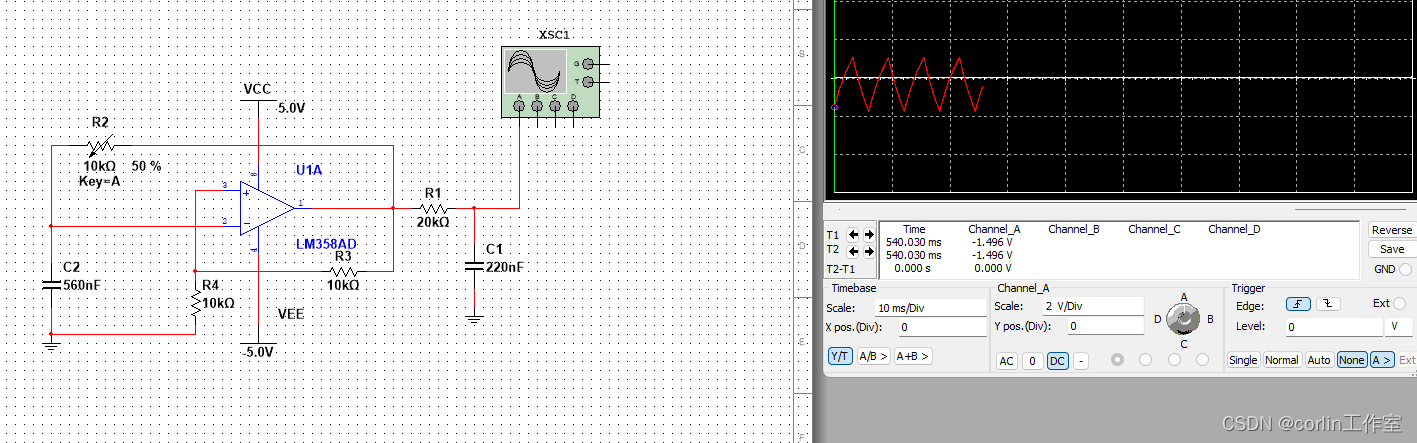
Multisim14.0仿真(五)三角波发生器
一、仿真原理图: 二、仿真效果:...
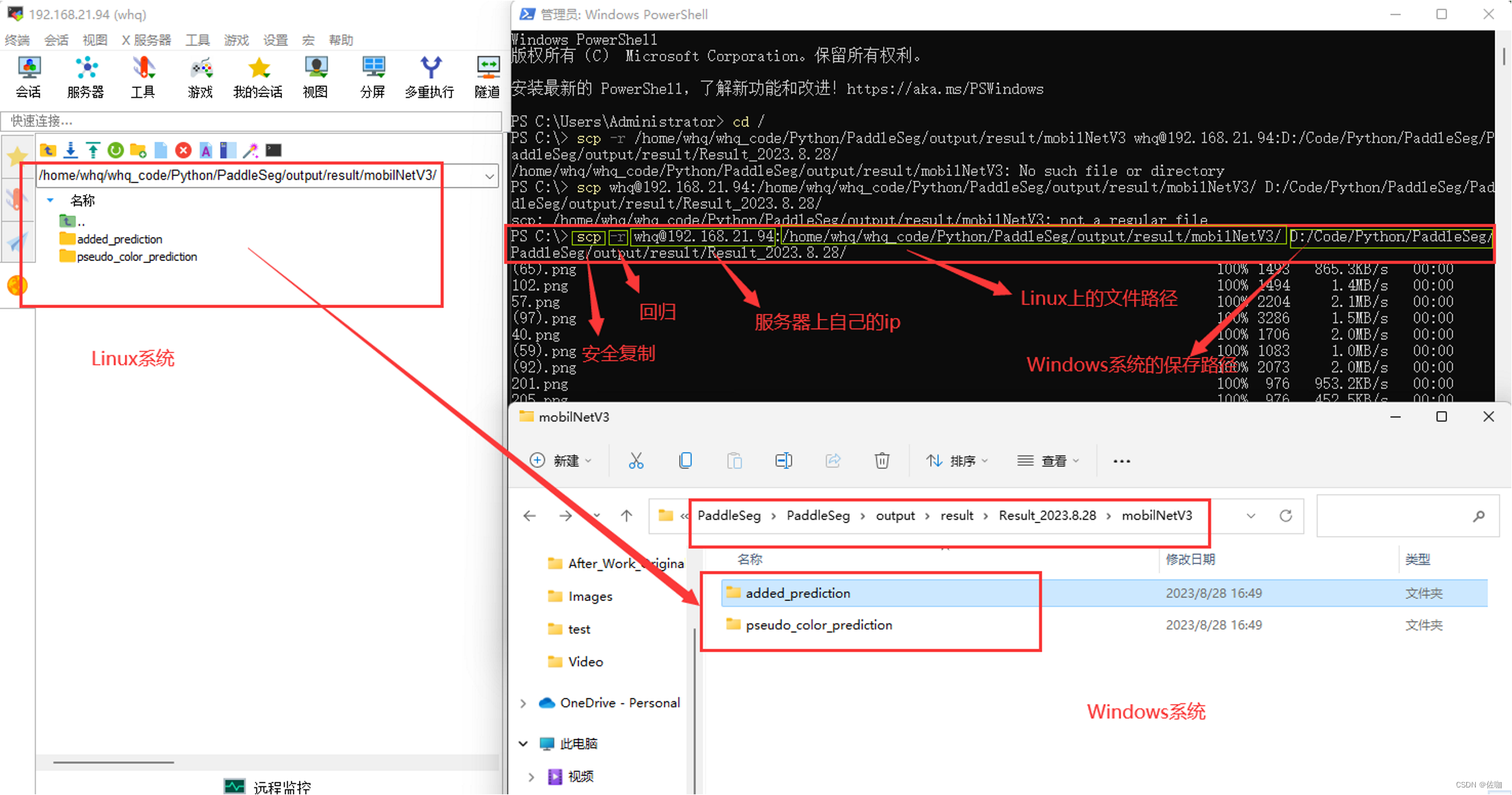
使用安全复制命令scp在Windows系统和Linux系统之间相互传输文件
现在已经有很多远程控制服务器的第三方软件平台,比如FinalShell,MobaXterm等,半可视化界面,使用起来非常方便和友好,两个系统之间传输文件直接拖就行,当然也可以使用命令方式在两个系统之间相互传递。 目录…...
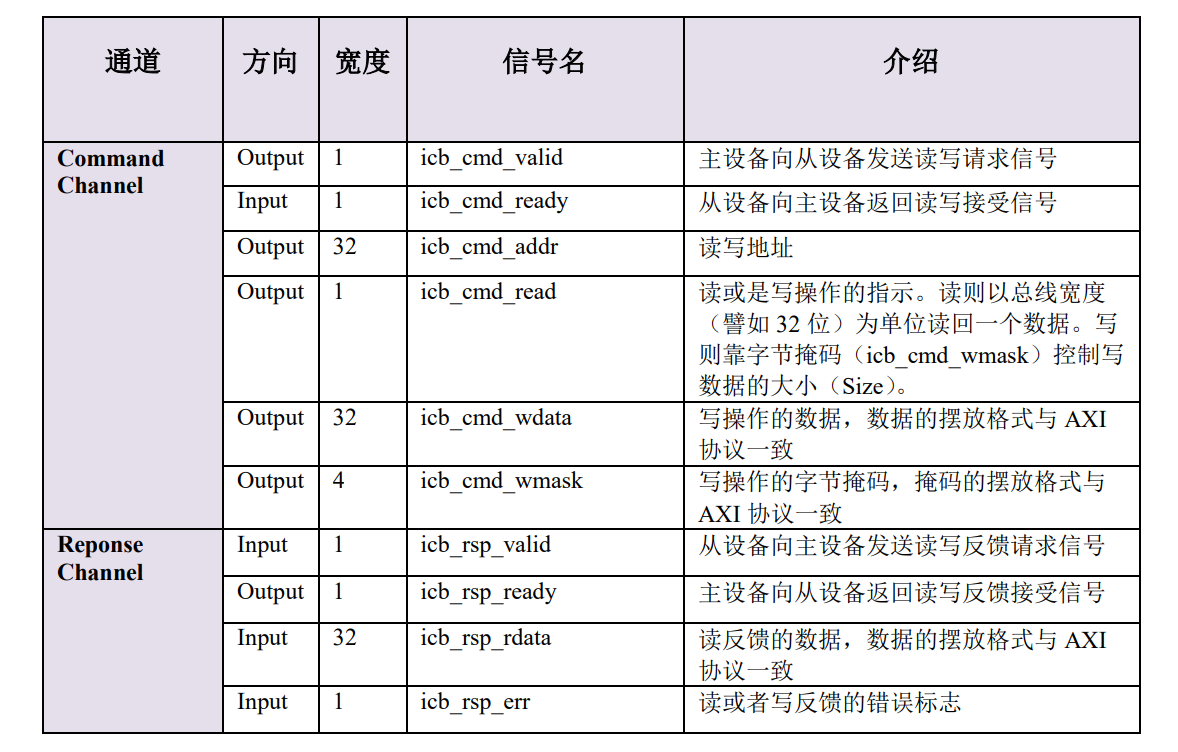
SOC总线学习记录之ICB(Internal Chip Bus)
蜂鸟E203总线: 采用自定义总线协议 ICB(Internal Chip Bus),该总线用于蜂鸟 E203 内核内部使用,同时也可作为 SoC 中的总线使用。 ICB 总线的初衷是为了能够尽可能地结合 AXI 总线和 AHB 总线的优点,兼具高…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
