代码随想录Day_52打卡
①、最长递增子序列
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
事例:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
思路:
使用动态规划,dp含义:dp[i]表示数组nums到下标为i时的最长递增子序列,由于涉及到删除数字,故每个数字都应该往前面比较,故在赋值时,应取dp[i]和dp[j] + 1的最大值。
动态规划:
dp定义及含义:dp[i]表示到nums[i]时的最长递增子序列
状态转移方程:if(nums[i] == nums[j]) dp[i] = Math.max(dp[i],dp[j] + 1) j为0到i - 1
初始化:全部填充为1 因为不包括空集
遍历顺序:外层遍历数组,内层遍历0到i - 1
dp中的最大值即为答案。
代码:
public int lengthOfLIS(int[] nums) {if(nums.length == 1) return 1;int[] dp = new int[nums.length];Arrays.fill(dp,1);int res = 1;for(int i = 1;i < nums.length;i++){for(int j = 0;j < i;j++){if(nums[i] > nums[j]) dp[i] = Math.max(dp[i],dp[j] + 1);}res = Math.max(dp[i],res);}return res;}②、最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标
l和r(l < r)确定,如果对于每个l <= i < r,都有nums[i] < nums[i + 1],那么子序列[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]就是连续递增子序列。
事例:
输入:nums = [1,3,5,4,7] 输出:3 解释:最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
思路:
跟上一题类似,只是要求连续,使用动态规划的话,只需要在改动下状态转移方程。上一题中,内层套用for循环遍历取得最大值,本质就是跳过其中的一些数达到删除效果,这题要求连续,则删除for循环,只需与前一个数比较即可。
动态规划:
dp定义及含义:dp[i]表示到nums[i]时的最长连续递增序列
状态转移方程:if(dp[i] == dp[i - 1]) dp[i] = dp[i - 1] + 1
初始化:全部填充为1 因为不包括空集
遍历顺序:从左到右遍历数组nums
dp中的最大值即为答案。
代码:
public int findLengthOfLCIS(int[] nums) {//动态规划// if(nums.length == 1) return 1;// int[] dp = new int[nums.length];// Arrays.fill(dp,1);// int res = 1;// for(int i = 1;i < nums.length;i++){// if(nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;// res = Math.max(res,dp[i]);// }// return res;int res = 1;int count = 1;for(int i = 1;i < nums.length;i++){if(nums[i] > nums[i - 1]) count++;else{res = Math.max(res,count);count = 1;}}res = Math.max(res,count);return res;}③、最长重复子数组
给两个整数数组
nums1和nums2,返回 两个数组中 公共的 、长度最长的子数组的长度 。
事例:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7] 输出:3 解释:长度最长的公共子数组是 [3,2,1] 。
思路:
这题涉及到匹配过程,由于有两个数组,长度可能不同,则dp需要两个维度记录。创建dp数组,其中dp[i][j]表示nums1从0到i - 1与nums2从0到j - 1的最长重复子数组,其中dp[i][j]只能从dp[i - 1][j - 1]推导,且第一行和第一列没实际意义,初始化为0。
动态规划:
dp定义及含义:dp[i][j]表示nums1从0到i - 1与nums2从0到j - 1的最长重复子数组
状态转移方程:if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1
初始化:第一行和第一列初始化为0
遍历顺序:嵌套遍历两个nums数组,其中要注意i、j与数组的对应关系
dp中的最大值即为答案。
代码:
public int findLength(int[] nums1, int[] nums2) {//二维数组int[][] dp = new int[nums1.length + 1][nums2.length + 1];int res = 0;for(int i = 1;i < nums1.length + 1;i++){for(int j = 1;j < nums2.length + 1;j++){if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;res = Math.max(res,dp[i][j]);}}return res;}与背包问题类似:也可以转化为一维数组,此时dp[j]表示nums2从0到j与nums1的最长重复子数组,由前面的二维数组dp可看出,dp的赋值依赖于前一行或前一列的结果,故从上到下将值覆盖可以将dp简化为一维数组。套用两层for循环,如果匹配,dp[j] = dp[j - 1] + 1,不匹配则赋为0.
动态规划:
dp定义及含义:dp[j]表示nums2从0到j - 1与nums1的最长重复子数组
状态转移方程:if(nums1[i - 1] == nums2[j - 1]) dp[j] = dp[j - 1] + 1
初始化:全部初始化为0
遍历顺序:嵌套遍历两个nums数组,先遍历nums1(作为行),再从大到小遍历nums2,避免重复比较。
dp中的最大值即为答案。
代码:
public int findLength(int[] nums1, int[] nums2) {//二维数组// int[][] dp = new int[nums1.length + 1][nums2.length + 1];// int res = 0;// for(int i = 1;i < nums1.length + 1;i++){// for(int j = 1;j < nums2.length + 1;j++){// if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;// res = Math.max(res,dp[i][j]);// }// }// return res;//一维数组int[] dp = new int[nums2.length + 1];int res = 0;for(int i = 1;i < nums1.length + 1;i++){for(int j = nums2.length;j > 0;j--){if(nums1[i - 1] == nums2[j - 1]) dp[j] = dp[j - 1] + 1;else dp[j] = 0;res = Math.max(res,dp[j]);}}return res;}参考:代码随想录 (programmercarl.com)
相关文章:

代码随想录Day_52打卡
①、最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序…...

692. 前K个高频单词
题目来源:力扣 题目描述: 给定一个单词列表 words 和一个整数 k ,返回前 k 个出现次数最多的单词。 返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序 排序。 示例 1: 输入:…...

介绍 Docker 的基本概念和优势,以及在应用程序开发中的实际应用
Docker 是一个开源的容器化平台,可以让开发者将应用程序和其所依赖的组件(如库、运行环境)打包成一个可移植、自包含的容器。这个容器可以在任何支持 Docker 的环境中运行,包括开发、测试、生产等环境。Docker 的基本概念包括以下…...

C++:构建一个二叉树的代码
#include <iostream>// 定义二叉树节点 struct BinaryTreeNode {int data;BinaryTreeNode* left;BinaryTreeNode* right;BinaryTreeNode(int val) : data(val), left(nullptr), right(nullptr) {} };// 构建二叉树 BinaryTreeNode* buildBinaryTree() {int val;std::ci…...
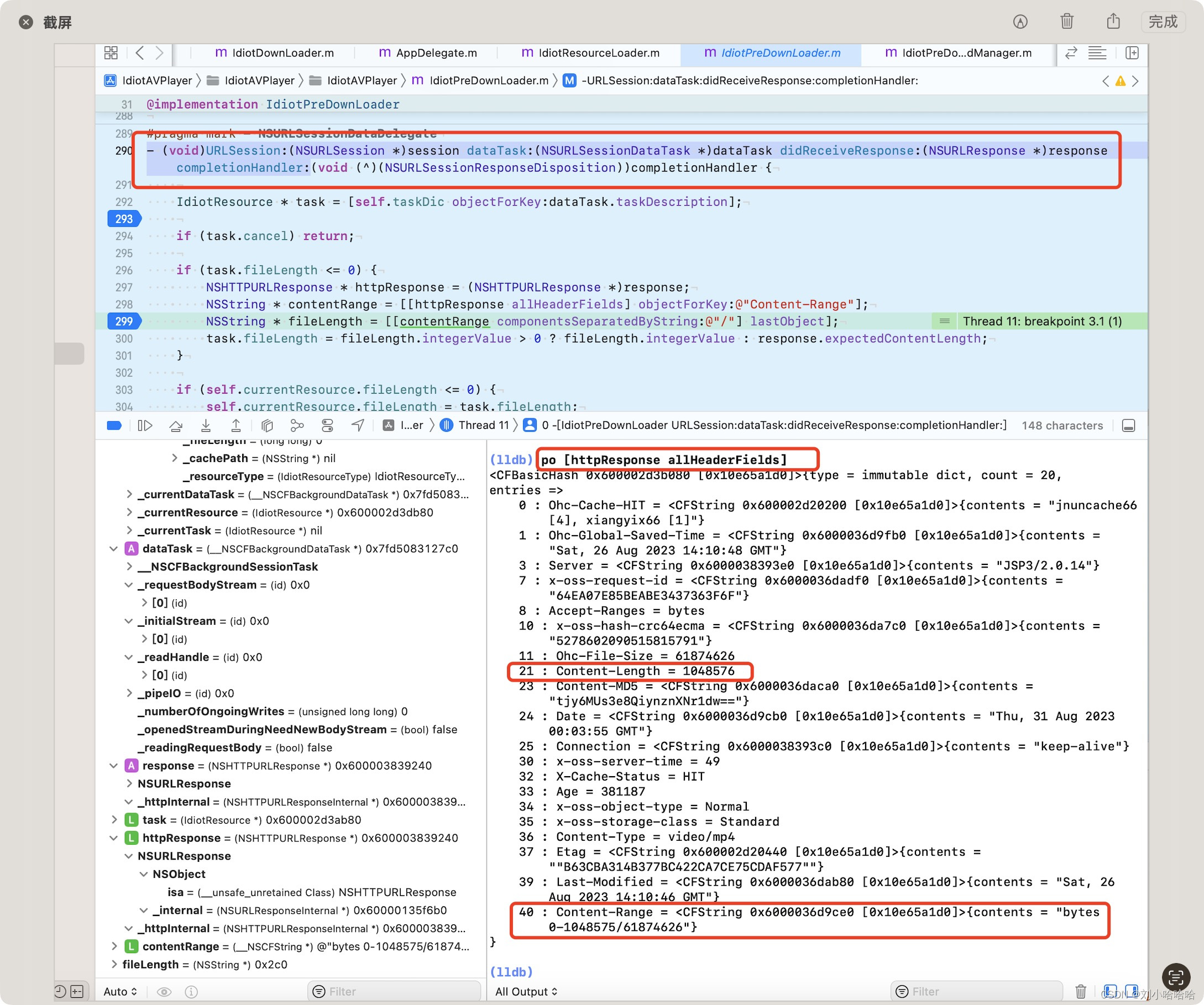
iOS 设置下载部分文件,如何获取完整文件的大小
在视频的需求中,遇到这样一个需求,播放一视频的时候,要预下载 后面10条视频,但是只下载后面十条视频的前面1M 实现方法 1 创建请求时设置cacheLength resource [[IdiotResource alloc] init];resource.requestURL task.request…...

如何助力金融贷款企业实现精准营销获客
无论是哪个行业,吸引客户都是核心。 许多公司的线下渠道面临着许多障碍,以至于他们不得不采用在线客户获取方法。受影响最大的行业之一是贷款行业。如何获得准确的贷款客户资源?如何赢得客户已经成为企业的一大痛点。 过去,信贷…...
或回车(\r)符号不起作用的解决办法、br、white、space、pre、line)
html中的换行(\n)或回车(\r)符号不起作用的解决办法、br、white、space、pre、line
文章目录 前言html不解释空白字符CSS样式的影响特定的文本区域white-space 前言 如果您的HTML中的换行和回车符号(\n和\r)似乎不起作用,可能有几种可能的原因: html不解释空白字符 在HTML中,连续的空白字符࿰…...

SpringBoot+MyBatisPlus+MySql+vue2+elementUi的案例、java访问数据库服务、java提供接口服务
文章目录 前言后端关键代码前端关键代码完整代码 前言 1、项目不使用前后端分离。 2、在创建SpringBoot的时候要注意各个插件间的版本问题。 3、后端技术SpringBootMyBatisPlusMySql。 4、前端技术vue2elementUi。 后端关键代码 简单介绍 1、数据库名称ssm_db 2、表名称tbl_bo…...

设计模式入门(二)观察者模式
设计模式入门 本系列所有内容参考自《HeadFirst设计模式》。因为书中的代码是采用java语言写的,博主这里用C语言改写。 这里采用讲故事的方式进行讲解。若有错误之处,非常欢迎大家指导。 设计模式:模式不是代码,而针对设计问题的…...

列化复杂的xml对应的类
你能帮我写一个序列化复杂的xml对应的类吗? c#代码 好的,可以试着为一个复杂的XML生成对应的C#类。这里我就简单的XML为例: <Book><Name>Design Patterns</Name><Author>Erich Gamma</Author><Pages>395</Pages><Chapters>…...
?)
什么是软件开发生命周期(SDLC)?
软件开发生命周期(SDLC)指的是从软件项目开始到最终交付的整个过程。它是软件开发过程的指导框架,用于规划、开发、测试、部署和维护软件系统。 SDLC包含了一系列阶段,每个阶段都有特定的任务、活动和产物。这些阶段通常包括以下…...

计算机视觉中常用的角点检测算法及其作用
角点检测是计算机视觉中的重要任务,用于识别图像中的角点或关键点。以下是一些常用的角点检测算法: Harris角点检测:Harris角点检测是一种经典的角点检测算法,它通过计算图像中每个像素的角点响应函数来检测角点。Harris角点检测对…...
css3英文文字换行,超过两行...展示
需求:超过两行...展示 开发的过程中发现div内容中文可以换行英文不换行,导致长度会溢出。 是英文全英文的话浏览器会解析成一个单词, 加上这句就好了 word-break:break-all; 一开始不知道是会解析成一个单词,用字符串拼接处理…...

查各种金属非金属材料的物性参数方法
背景 上面给了任务,要做调研,各种材料的各种参数,高温的、低温的、常温的、常压的、高压的、低压的。 网上搜出来很多材料的参数都是各种卖材料的厂商给出的,也不晓得他们的测量结果可不可信,有没有一个权威机构背书…...

【数据库】查询PostgreSQL中所有表逻辑外键
引言 在PostgreSQL数据库中,逻辑外键是用于约束表之间关系的一种机制。然而,在某些情况下,我们可能需要删除和重建逻辑外键。本文将介绍如何查询PostgreSQL中所有表的逻辑外键,并指导您如何先删除再重新建立这些外键。 查询Post…...
【Kubernetes理论篇】2023年最新CKA考题+解析
文章目录 第一题:RBAC授权访问控制第二题:Node节点维护第三题:K8S集群版本升级第四题:ETCD数据库备份恢复第五题:NetworkPolicy网络策略第六题:Service四层负载第七题:Ingress七层负载第八题&am…...
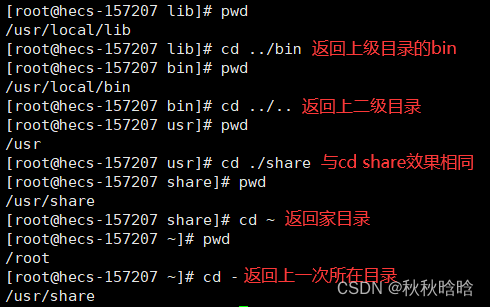
【Linux】目录结构、路径
目录 1. 目录结构 1.1 基本概念 1.2 具体的目录结构 2. 路径 2.1 绝对路径和相对路径 2.2 特殊路径符 1. 目录结构 1.1 基本概念 Linux的目录结构是一个树形结构。 Windows系统可以拥有多个盘符,如 C盘、D盘、E盘。Linux没有盘符这个概念,只有一…...

Java-集合框架-List,Set,Map,队列
文章目录 Java集合框架:List,Set,Map,队列Java集合框架是什么?如何使用?ListSetMap队列 什么场景使用?优缺点是什么?ListSetMap队列 Java示例List示例Set示例Map示例队列示例 对比 J…...

第一章_线程基础知识
先拜拜大神 Doug Lea(道格.利) java.util.concurrent在并发编程中使用的工具包 为什么学习并用好多线程极其重要 硬件方面 摩尔定律失效 摩尔定律:它是由英特尔创始人之一Gordon Moore(戈登.摩尔)提出来的。其内容为…...
定时关机解决方案)
linux(centos7)定时关机解决方案
使用场景与痛点: 根据实际需求,每个星期五都要关闭服务器若干,痛点如下: 1是服务器比较多,按起来麻烦。2是因为周五时间点特殊,着急下班容易忘记关闭服务器。那些要关注才能看的博客,不是我喷&a…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
