CCF-CSP 26次 第三题【角色授权】
计算机软件能力认证考试系统
20分:
#include<bits/stdc++.h>
using namespace std;
const int N=440;
int n,m,q,nv,no,nn,ns,ng;
struct Node
{string name;map<string,int>op;map<string,int>res_kind;map<string,int>res_name;
}role[N];
map<string,string>mp;
int main()
{scanf("%d %d %d",&n,&m,&q);for(int i=0;i<n;i++){cin>>role[i].name;scanf("%d",&nv);while(nv--){string s;cin>>s;}scanf("%d",&no);while(no--){string s;cin>>s;}scanf("%d",&nn);while(nn--){string s;cin>>s;}}string s1,s2,s3;for(int i=0;i<m;i++){cin>>s1>>ns>>s2>>s3;}for(int i=0; i<q; i++){string s,str1,str2,str3;cin>>s>>ng;string ss;cin>>ss;cin>>str1>>str2>>str3;if(s2=="u"){if(s3==s)printf("1\n");elseprintf("0\n");}else if(s2=="g"){if(s3==ss)printf("1\n");elseprintf("0\n");}}return 0;
}
100分:
需要注意提速之后,scanf与cin不能同时用
#include<iostream>
#include<vector>
#include<set>
#include<unordered_map>
using namespace std;
#pragma GCC optimize(2)struct User{string name;set<string> op;set<string> cat;set<string> list;
};
// 记录某些用户或组关联了哪些角色
// 实际上组和用户没必要区分,统一看作用户
unordered_map<string, vector<int>> to_users;int main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);//提速,cin与scnaf不能同时用int n, m, q;cin >> n >> m >> q;vector<User> users(n);// Usersstring tmp;for(int i = 0; i < n; i ++){cin >> tmp;users[i].name = tmp;int nv, no, nn;// operationscin >> nv;while(nv--){cin >> tmp;users[i].op.insert(tmp);}// categorycin >> no;while(no--){cin >> tmp;users[i].cat.insert(tmp);}// listcin >> nn;while(nn--){cin >> tmp;users[i].list.insert(tmp);}}// 将用户或组绑定已有的角色while(m--){// cin >> tmp;int idx = -1;for(int i = 0; i < users.size(); i ++){if(users[i].name == tmp){idx = i;break;}}int ns;cin >> ns;string t1, t2;while(ns--){cin >> t1 >> t2;// push_back的是角色在users数组中的下标// 把用户和组都看做成用户,不区分身份,因此t1没用to_users[t2].push_back(idx);}}while(q--){cin >> tmp;int ng;cin >> ng;vector<string> group;// 加入关联的用户组(包含自己以及关联的用户和组)group.push_back(tmp);while(ng--) {cin >> tmp;group.push_back(tmp);}// check tmp1 tmp2 tmp3string tmp1, tmp2, tmp3;cin >> tmp1 >> tmp2 >> tmp3;bool flag1 = false, flag2 = flag1, flag3 = flag1;// 之后就是看组中这些用户关联的角色们是否有权限了// 满足一个就break,否则就重置三个flagfor(int i = 0; i < group.size(); i ++){int n = to_users[group[i]].size();for(int j = 0; j < n; j ++){if(users[to_users[group[i]][j]].op.count(tmp1) || users[to_users[group[i]][j]].op.count("*")) flag1 = true;if(users[to_users[group[i]][j]].cat.count(tmp2) || users[to_users[group[i]][j]].cat.count("*")) flag2 = true;if(users[to_users[group[i]][j]].list.size() == 0) flag3 = true;else{if(users[to_users[group[i]][j]].list.count(tmp3))flag3 = true;}if(flag1 && flag2 && flag3) break;else{flag1 = false;flag2 = flag1;flag3 = flag1;}}if(flag1 && flag2 && flag3) break;}if(flag1 && flag2 && flag3) cout << 1 << endl;else cout << 0 << endl;}
}
相关文章:

CCF-CSP 26次 第三题【角色授权】
计算机软件能力认证考试系统 20分: #include<bits/stdc.h> using namespace std; const int N440; int n,m,q,nv,no,nn,ns,ng; struct Node {string name;map<string,int>op;map<string,int>res_kind;map<string,int>res_name; }role[N];…...
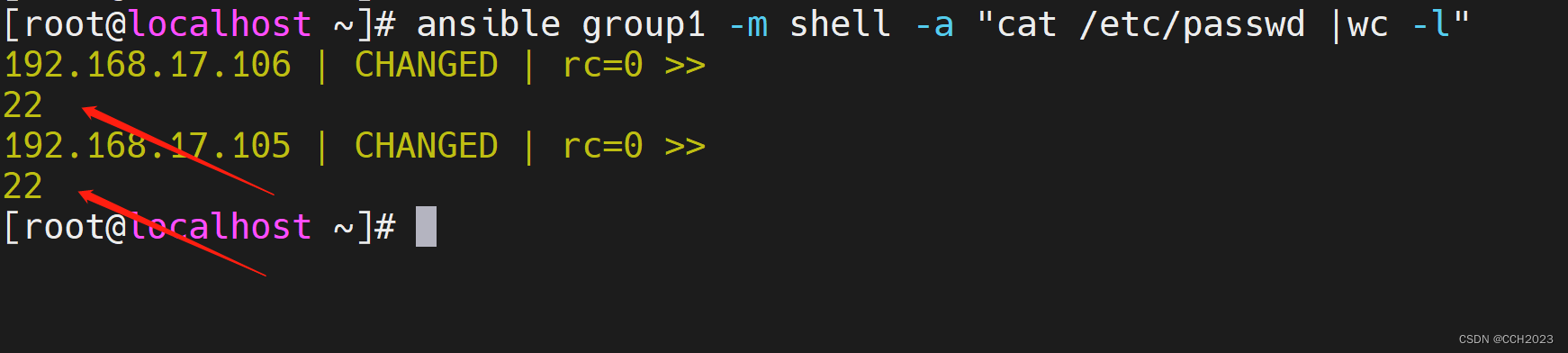
Ansible学习笔记11
Command和Shell模块: 两个模块都是用于执行Linux命令的,这个对于命令熟悉的工程师来说,用起来非常high。 Shell模块跟Command模块差不多(Command模块不能执行一类$HOME、> 、<、| 等符号,但是Shell是可以的。&…...
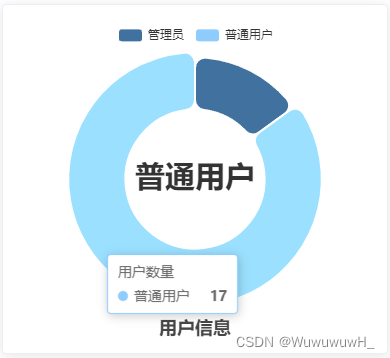
Vue中如何为Echarts统计图设置数据
在前端界面接收后端数据后,将数据赋值给ECharts中的data时出现了,数据读取失败的问题(可能是由于数据渲染的前后顺序问题)。后通过如下方式进行了解决: 1、接下来将介绍UserController中的countUsers方法,…...

力扣141. 环形链表
141. 环形链表 简单 2K 相关企业 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链…...

4.1 链式栈StackT
C关键词:内部类/模板类/头插 C自学精简教程 目录(必读) C数据结构与算法实现(目录) 栈的内存结构 空栈: 有一个元素的栈: 多个元素的栈: 成员函数说明 0 clear 清空栈 clear 函数负责将栈的对内存释放…...
:牛客在线编程10 贪心算法)
算法练习(10):牛客在线编程10 贪心算法
package jz.bm;import java.util.ArrayList; import java.util.Arrays;public class bm10 {/*** BM95 分糖果问题*/public int candy (int[] arr) {int res 0;int n arr.length;int[] nums new int[n];//每个人都分配一个糖果for (int i 0; i < n; i) {nums[i] 1;}//从…...

Java8新特性1——函数式接口lambda表达式
Java8新特性1——函数式接口&lambda表达式 注:以下内容基于Java 8,所有代码都已在Java 8环境下测试通过 目录: Java8新特性1——函数式接口&lambda表达式方法引用Stream 1. 函数式接口 如果在一个接口中,有且只有一个抽…...
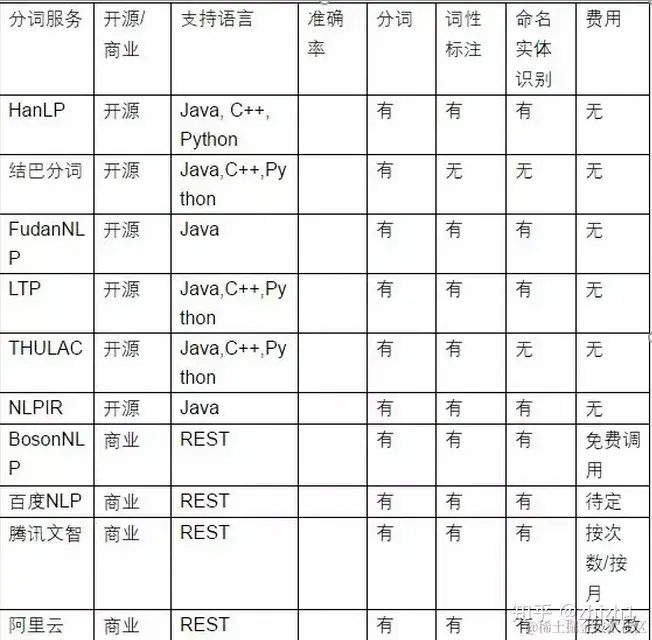
文本标注技术方案(NLP标注工具)
Doccano doccano 是一个面向人类的开源文本注释工具。它为文本分类、序列标记和序列到序列任务提供注释功能。您可以创建用于情感分析、命名实体识别、文本摘要等的标记数据。只需创建一个项目,上传数据,然后开始注释。您可以在数小时内构建数据集。 支持…...

03-使用一个不可变对象作为key,红黑树怎么比较大小?
使用一个不可变对象作为key,红黑树怎么比较大小? 答:Java 中的红黑树是通过左旋、右旋的方式来维护树的平衡性,而左旋、右旋又依赖于节点大小的比较。对于使用不可变对象作为key实际上是可以的,因为比较key的大小本身…...
)
2021江苏省赛热身赛 C Magic Rabbit(数形结合)
2021江苏省赛热身赛 C Magic Rabbit(数形结合) Magic Rabbit 非常好且巧妙地一道题。 大意:给出三种溶液 , 三种溶液分别含有不同浓度的 x ,y 两种物质。 溶液x (mg/ml)y (mg/ml)溶液1x1y1溶液2x2y2溶液3x3y3 给出 Q 组询问 ,…...
:AES代码实现解析)
AES加密(2):AES代码实现解析
在我的上一篇文章AES基础知识和计算过程中,大概介绍了AES(Rijndael)加密的整个过程。那么在这一篇文章中,就来看一下AES在代码中是如何实现的,也有助于我们理解其中的一些细节。 本篇文章所用的AES代码来源于Szymon Stefanek的开源C代码 文章…...

SpringBoot项目通过分词器生成词云
目录 前言一、词云是什么?二、使用步骤1.引入依赖2.application.yml3.Controller4.分词工具类4.词云生成工具类、支持输出文件和字节流 注意 前言 公司项目涉及到员工任务管理,需要从员工任务中获取任务信息生成个人词云图,可以把员工任务中…...

Nacos 配置管理及相关使用
文章目录 Nacos 配置管理一、统一配置管理1、在Nacos 中添加配置文件2、从微服务拉取配置3、配置实现步骤(1)引入 nacos-config 依赖(2)添加 bootstrap.yml(4)在 nacos 中添加配置 二、配置热更新1、配置热…...

重发布与路由策略
华子目录 重发布重发布条件重发布配置规则重发布名词配置命令ospf往rip重发布(重发布动态)静态往rip重发布(重发布静态)直连往rip重发布(重发布直连)rip往ospf重发布(重发布动态)静态…...
)
57. 插入区间(C++题解)
57. 插入区间 插入区间 给你一个无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 示例 1: 输入&#x…...

【数据结构Java版】 初识泛型和包装类
目录 1.包装类 1.1基本数据类型以及它们所对应的包装类 1.2装箱和拆箱 1.3自动装箱和自动拆箱 2.什么是泛型 3.引出泛型 4.泛型类的使用 4.1语法 4.2示例 4.3类型推导 5.泛型是如何编译的 5.1擦除机制 5.2正确的写法 6.泛型的上届 6.1语法 6.2示例 …...

Spring中如何解决循环依赖问题的三种方法
什么是循环依赖问题 在 Spring 中,循环依赖问题指的是两个或多个 bean 之间相互依赖形成的闭环。具体而言,当 bean A 依赖于 bean B,同时 bean B 也依赖于 bean A,就形成了循环依赖。 循环依赖问题在 Spring 容器中是一个非常常…...
【ArcGIS Pro二次开发】(65):进出平衡SHP转TXT、TXT转SHP
最近一个小伙伴提了这么一个需求,需要把TXT和SHP进行互转。 这种TXT文件其实遇到了好几个版本,都有一点小差异。之前已经做过一个TXT转SHP的工具,但好像不适用。于是针对这个版本,做了互转的2个工具。 【SHP转TXT】 一、要实现的…...

Shell开发实践:服务器的磁盘、CPU、内存的占用监控
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师…...
)
超详细 async和await 项目实战运用(附加文字解答+源码)
文章目录 问题描述async什么是 asyncasync 的作用async 的应用场景async 优点 await什么是 awaitawait 的作用await 的应用场景await 的优点async和 await结合使用 结束语 大家好!又到了愉快的周末假期,今天是2023年9月3日|农历七月十九,我最…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
