Day49|leetcode 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
leetcode 121. 买卖股票的最佳时机
题目链接:121. 买卖股票的最佳时机 - 力扣(LeetCode)
视频链接:动态规划之 LeetCode:121.买卖股票的最佳时机1_哔哩哔哩_bilibili
题目概述
给定一个数组 ,它的第 个元素 表示一支给定股票第 天的价格。pricesiprices[i]i
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 。0
示例 1:
输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
思路
1.确定dp数组含义:
dp[i][0] :第i天持有股票所得最多现金。
dp[i][1] :第i天不持有股票所得最多现金。
这里的“持有”和“不持有”不代表当天买入股票或者卖出股票,可能是前一天买的!!!
2.确定递推公式:(最开始现金为0元)
第i天持有股票:
1)当天就买进股票:-prices[i]
2)前一天买进股票:dp[i - 1][0]
所以dp[i][0] = max(dp[i - 1][0], -prices[i])
第i天不持有股票:
1)当天卖出股票:prices[i] + dp[i - 1][0]
2)前一天卖出股票:dp[i - 1][1]
所以dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0])
3.数组初始化:
dp[0][0] -= prices[0]
dp[0][1] = 0
4.确定遍历顺序:
从前向后
5.打印dp数组:
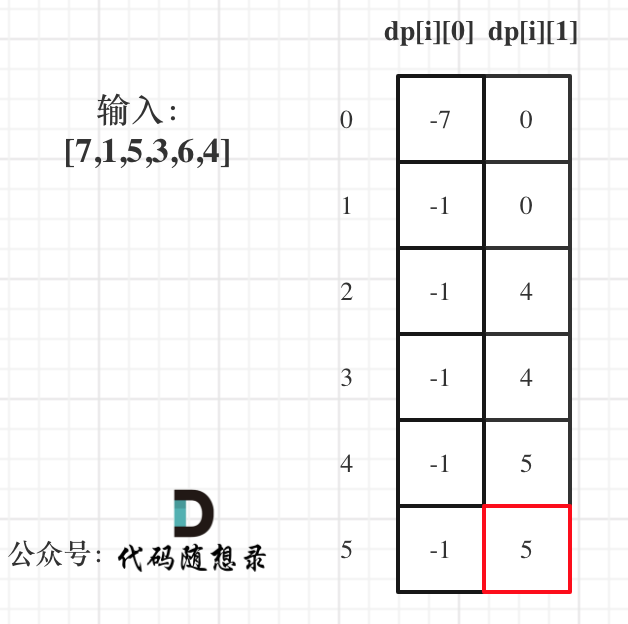
代码实现(动规)
class Solution {
public:int maxProfit(vector<int>& prices) {if(prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(),vector<int>(2));dp[0][0] -= prices[0];dp[0][1] = 0;for(int i = 1;i < prices.size();i++) {dp[i][0] = max(-prices[i],dp[i - 1][0]);dp[i][1] = max(prices[i] + dp[i - 1][0],dp[i - 1][1]);} return dp[prices.size() - 1][1];}
};代码实现(贪心)
class Solution {
public:int maxProfit(vector<int>& prices) {int low = INT_MAX;int result = 0;for (int i = 0; i < prices.size(); i++) {low = min(low, prices[i]); // 取最左最小价格result = max(result, prices[i] - low); // 直接取最大区间利润}return result;}
};leetcode 122.买卖股票的最佳时机II
题目链接:122. 买卖股票的最佳时机 II - 力扣(LeetCode)
视频链接:动态规划,股票问题第二弹 | LeetCode:122.买卖股票的最佳时机II_哔哩哔哩_bilibili
题目概述
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4] 输出:7 解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 。
思路
本题和上一题没有多大区别,唯一区别就是本题可以多次买卖,在动规五部曲分析上也只有递归公式上有区别。
第i天持有股票:
1)当天就买进股票:dp[i - 1][1] - prices[i](这里是和上一题唯一不一样的区别,因为上道题最开始手里的钱是0元,所以是'0 - prices[i]'只不过把0给省略了,而这道题可以多次买卖股票,如果是当天买进股票的话,那么所得现金就是昨天不持有股票的所得现金 - 今天的股票价格)
2)前一天买进股票:dp[i - 1][0]
所以dp[i][0] = max(dp[i - 1][0], -prices[i])
第i天不持有股票:dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0])
代码实现(动规)
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(len, vector<int>(2, 0));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[len - 1][1];}
};代码实现(贪心)
class Solution {
public:int maxProfit(vector<int>& prices) {int result = 0;for(int i = 1;i < prices.size();i++) {result += max(prices[i] - prices[i - 1],0);}return result;}
};相关文章:

Day49|leetcode 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
leetcode 121. 买卖股票的最佳时机 题目链接:121. 买卖股票的最佳时机 - 力扣(LeetCode) 视频链接:动态规划之 LeetCode:121.买卖股票的最佳时机1_哔哩哔哩_bilibili 题目概述 给定一个数组 ,它的第 个元…...
【项目经验】:elementui表格中表头的多选框换成文字
一.项目需求 表格可以多选,表头都是汉字。。。。类似于这种 二.实现功能 用到的方法 Table Attributes 参数说明类型可选值默认值header-cell-class-name表头单元格的 className 的回调方法,也可以使用字符串为所有表头单元格设置一个固定的 className。…...
【LeetCode】剑指 Offer <二刷>(4)
目录 题目:剑指 Offer 09. 用两个栈实现队列 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 10- I. 斐波那契数列 - 力扣&am…...

CentOS7查看和关闭防火墙
CentOS 7.0默认使用的是firewall作为防火墙 查看防火墙状态 firewall-cmd --state1 停止firewall systemctl stop firewalld.service1 禁止firewall开机启动 systemctl disable firewalld.service 1 转自:CentOS 6和CentOS 7防火墙的关闭 Centos7开放及查看…...
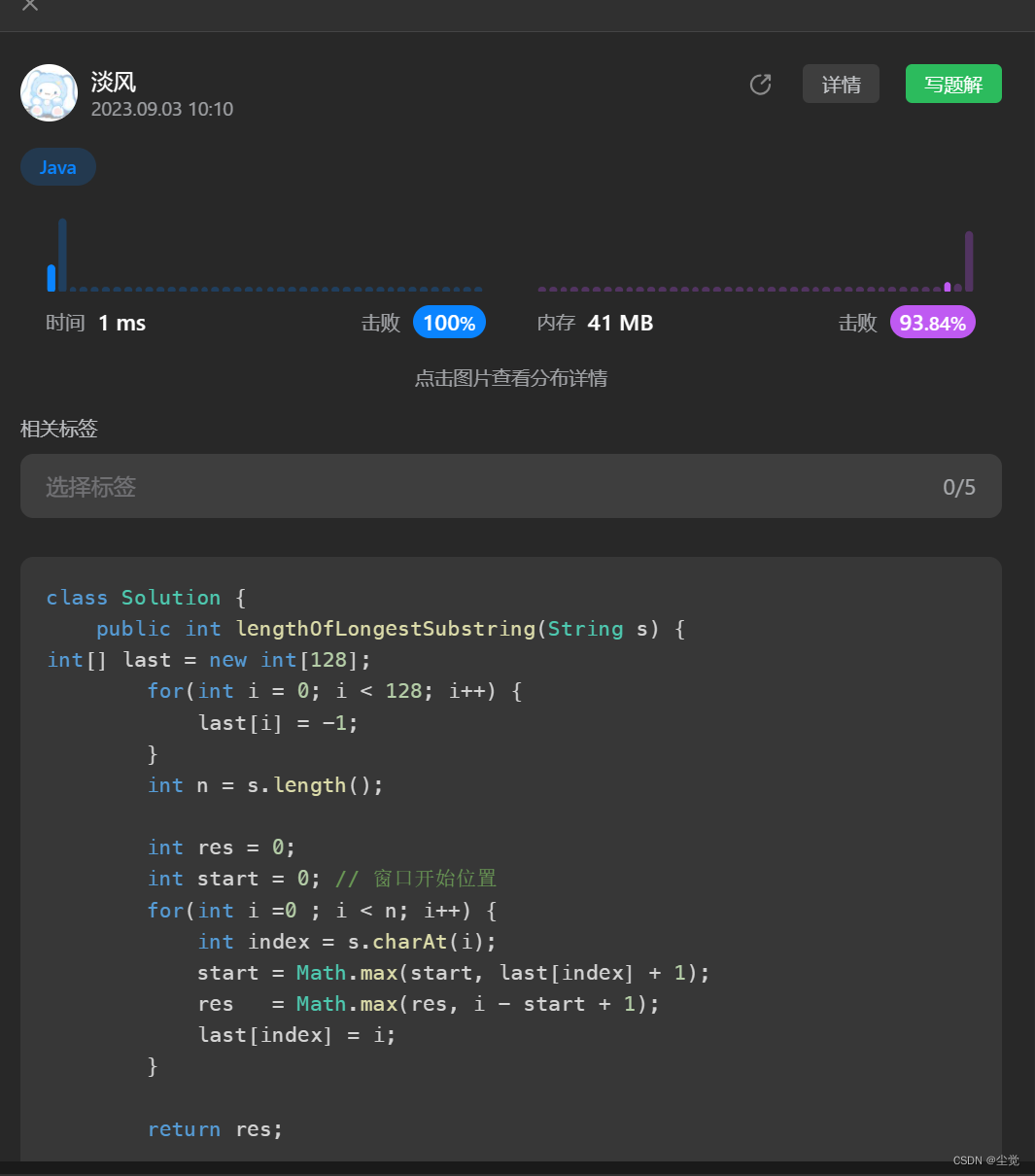
LeetCode 无重复字符的最长子串 打败100%的人
😀前言 LeetCode上的“无重复字符的最长子串”问题要求我们找到给定字符串中不包含重复字符的最长子串的长度。这个问题是一个典型的滑动窗口技巧的应用,需要有效地处理字符出现的情况来找到解决方案。 . 在本解决方案中,我们将探讨两种不同的…...
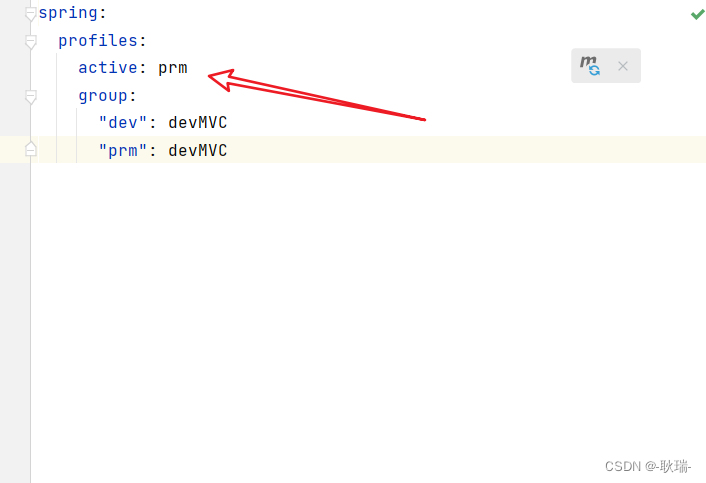
Spring Boot中通过maven进行多环境配置
上文 java Spring Boot将不同配置拆分入不同文件管理 中 我们说到了,多环境的多文件区分管理 说到多环境 其实不止我们 Spring Boot有 很多的东西都有 那么 这就有一个问题 如果 spring 和 maven 都配置了环境 而且他们配的不一样 那么 会用谁的呢? 此…...

python自动化Selenium的使用
python自动化Selenium的使用 Selenium是一个自动化测试框架,用于模拟和控制浏览器操作,支持多种编程语言。它可以模拟人类用户在浏览器上的操作(如点击、滚动、输入等),并检查网页内容和元素的属性。Selenium可用于对…...
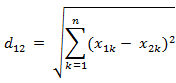
大数据课程K13——Spark的距离度量相似度度量
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Spark的距离度量和相似度度量; ⚪ 掌握Spark的欧氏距离; ⚪ 掌握Spark的曼哈顿距离; ⚪ 掌握Spark的切比雪夫距离; ⚪ 掌握Spark的最小二乘法; 一、距离度量和相似度度量 1. …...

Lambda表达式第四版
1、冗余的Runnbale代码 package com.lambda;public class Demo01Runnable {public static void main(String[] args) {RunnableImpl runnable new RunnableImpl();Thread thread new Thread(runnable);thread.start();//Lambda表达式} }class RunnableImpl implements Runnab…...

自定义类加载器
java中自定义类加载器,并将双亲委派改为逆向双亲委派 自定义类加载器JarLoader: package cn.ac.iscas.dmo.common.tools.core.classloader;import org.apache.commons.collections4.MapUtils;import java.io.*; import java.net.URL; import java.net.U…...

【Redis】Redis 的学习教程(七)之 SpringBoot 集成 Redis
在前几篇文章中,我们详细介绍了 Redis 的一些功能特性以及主流的 java 客户端 api 使用方法。 在当前流行的微服务以及分布式集群环境下,Redis 的使用场景可以说非常的广泛,能解决集群环境下系统中遇到的不少技术问题,在此列举几…...
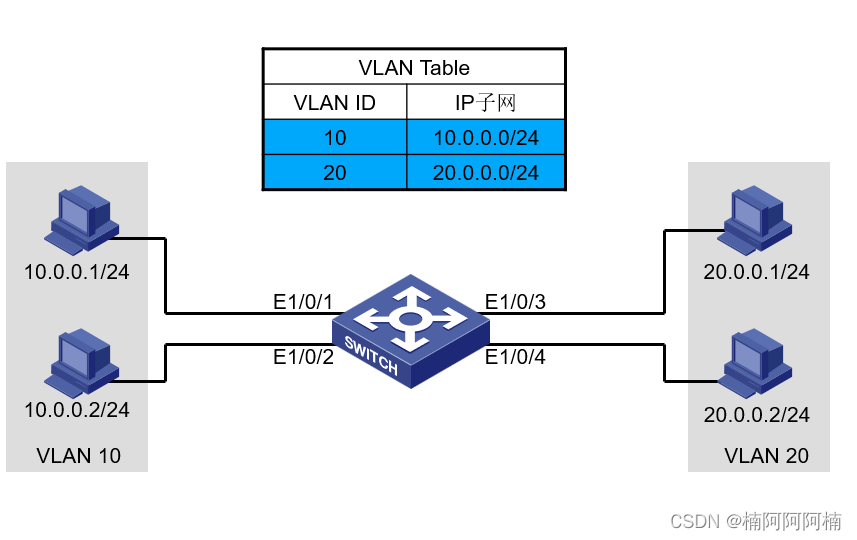
Vlan和Trunk
文章目录 一、VLAN的定义与背景1. 传统以太网的问题(广播域)2. 用VLAN隔离广播域3. VLAN的优点与应用 二、VLAN的转发过程举例三、802.1Q标签:帧格式与作用四、VLAN工作原理交换机端口类型AccessTrunkHybrid PVID(Port VLAN ID&am…...
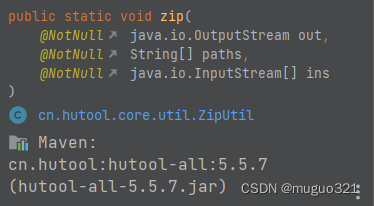
java 批量下载将多个文件(minio中存储)压缩成一个zip包
我的需求是将minio中存储的文件按照查询条件查询出来统一压成一个zip包然后下载下来。 思路:针对这个需求,其实可以有多个思路,不过也大同小异,一般都是后端返回流文件前端再处理下载,也有少数是压缩成zip包之后直接给…...

nnUNet v2数据准备及格式转换 (二)
如果你曾经使用过nnUNet V1,那你一定明白数据集的命名是有严格要求的,必须按照特定的格式来进行命名才能正常使用。 这一节的学习需要有数据,如果你有自己的数据,可以拿自己的数据来实验,如果没有,可以用十…...

ant-vue1.78版监听a-modal遮罩层的滚动事件
监听a-modal遮罩层的滚动事件 我们开发过程中经常有遇到监听页面滚动的事件需求,去做一些下拉加载或者是下拉分页的需求,我们直接在vue的生命周期中去绑定事件监听非常的方便,但如果是弹框的遮罩层的滚动监听呢?页面的监听完全是…...
MATLAB中residue函数用法
目录 语法 说明 示例 求解具有实根的部分分式展开式 展开具有复数根和同次分子及分母的分式 展开分子次数高于分母次数的分式 residue函数的功能是部分分式展开(部分分式分解)。 语法 [r,p,k] residue(b,a) [b,a] residue(r,p,k) 说明 [r,p…...
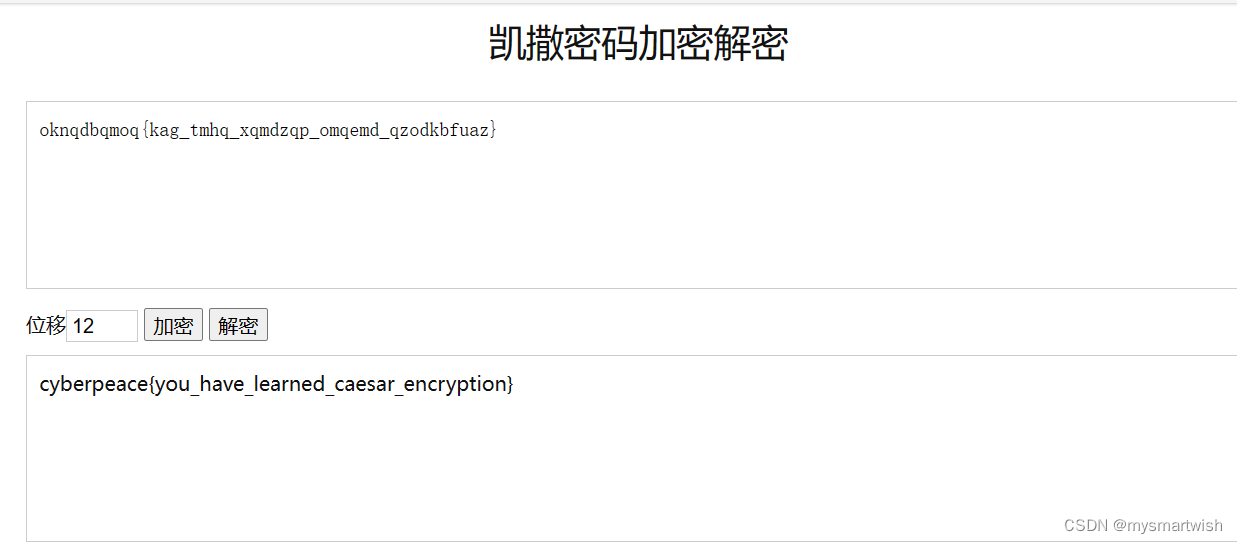
攻防世界-Caesar
原题 解题思路 没出现什么特殊字符,可能是个移位密码。凯撒密码加密解密。偏移12位就行。...

嵌入式开发-lin总线介绍 一.概述
1.1lin总线定义和历史 LIN总线(Local Interconnect Network)是一种基于UART/SCI(Universal Asynchronous Receiver-Transmitter/Serial Communication Interface)的低成本串行通信协议。它主要用于汽车、家电、办公设备等多种领域…...
羊城杯-2023-Crypto
文章目录 Danger_RSA题目描述:题目分析: Easy_3L题目描述:题目分析: XOR贯穿始终题目描述:题目分析: MCeorpkpleer题目描述:题目分析: SigninCrypto题目描述:题目分析&am…...
RabbitMQ快速上手及讲解
前言:在介绍RabbitMQ之前,我们先来看下面一个场景: 1.1.1.1 异步处理 场景说明: 用户注册后,需要发注册邮件和注册短信,传统的做法有两种 1.串行的方式 (1)串行方式:将注册信息写入数据库后&a…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
