MATLAB中residue函数用法
目录
语法
说明
示例
求解具有实根的部分分式展开式
展开具有复数根和同次分子及分母的分式
展开分子次数高于分母次数的分式
residue函数的功能是部分分式展开(部分分式分解)。
语法
[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)说明
[r,p,k] = residue(b,a) 计算以如下形式展开的两个多项式之比的 部分分式展开式 的留数、极点和直项
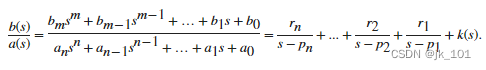
residue 的输入是由多项式 b = [bm ... b1 b0] 和 a = [an ... a1 a0] 的系数组成的向量。输出为留数 r = [rn ... r2 r1]、极点 p = [pn ... p2 p1] 和多项式 k。对于大多数教科书问题,k 为 0 或常量。
[b,a] = residue(r,p,k) 将部分分式展开式转换回两个多项式之比,并将系数返回给 b 和 a。
示例
求解具有实根的部分分式展开式
使用 residue 求以下多项式之比 F(s) 的部分分式展开式
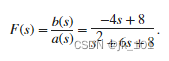
b = [-4 8];
a = [1 6 8];
[r,p,k] = residue(b,a)
r = 2×1-128p = 2×1-4-2k =[]此结果代表以下部分分式展开式
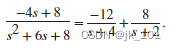
使用 residue 将部分分式展开转换回多项式系数。
[b,a] = residue(r,p,k)
b = 1×2-4 8a = 1×31 6 8
此结果表示初始分式 F(s)。
展开具有复数根和同次分子及分母的分式
如果分子的次数与分母的次数相等,输出 k 可以是非零值。
求解具有复数根和同次分子和分母的两个多项式 F(s) 之比的部分分式展示式,其中 F(s) 为
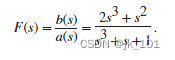
b = [2 1 0 0];
a = [1 0 1 1];
[r,p,k] = residue(b,a)
r = 3×1 complex0.5354 + 1.0390i0.5354 - 1.0390i-0.0708 + 0.0000ip = 3×1 complex0.3412 + 1.1615i0.3412 - 1.1615i-0.6823 + 0.0000ik = 2residue 返回代表部分分式展开式的复数根和极点,以及常项 k
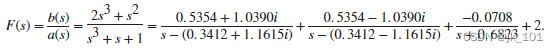
展开分子次数高于分母次数的分式
当分子次数大于分母次数时,输出 k 为代表 s 中多项式系数的向量。
使用 residue 执行 F(s) 的以下部分分式展开式。
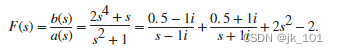
b = [2 0 0 1 0];
a = [1 0 1];
[r,p,k] = residue(b,a)
r = 2×1 complex0.5000 - 1.0000i0.5000 + 1.0000ip = 2×1 complex0.0000 + 1.0000i0.0000 - 1.0000ik = 1×32 0 -2
k 代表多项式![]()
参数说明:
b — 分子多项式的系数
a — 分母多项式的系数
r — 部分分式展开式残差
p — 部分分式展开式的极点
k — 直项(直项,以数字行向量的形式返回,这些数字按 s 的降幂指定多项式的系数。)
相关文章:
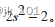
MATLAB中residue函数用法
目录 语法 说明 示例 求解具有实根的部分分式展开式 展开具有复数根和同次分子及分母的分式 展开分子次数高于分母次数的分式 residue函数的功能是部分分式展开(部分分式分解)。 语法 [r,p,k] residue(b,a) [b,a] residue(r,p,k) 说明 [r,p…...
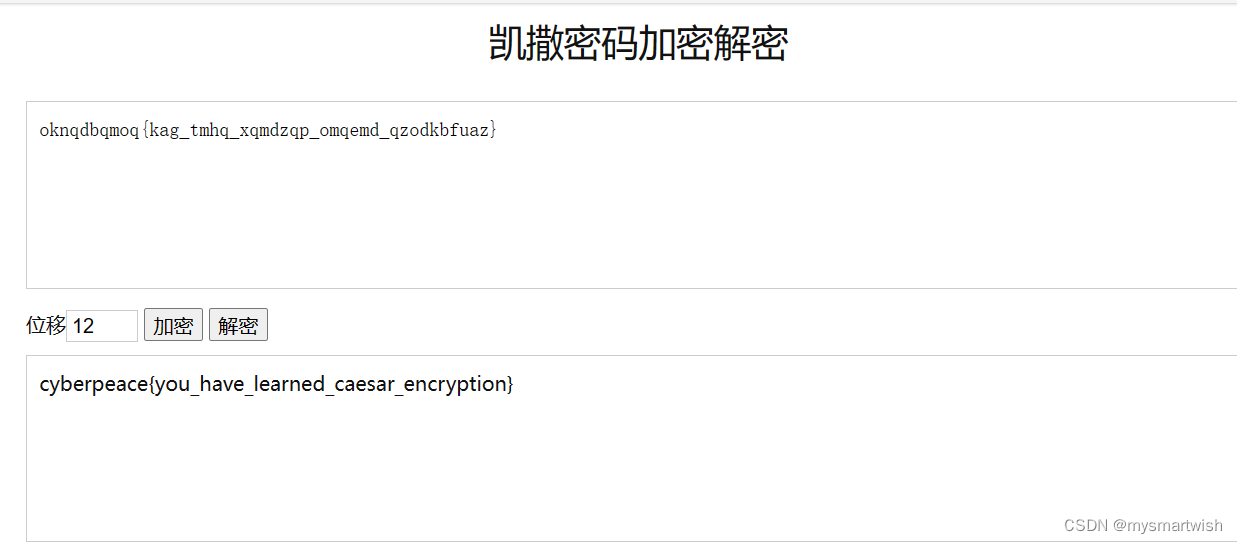
攻防世界-Caesar
原题 解题思路 没出现什么特殊字符,可能是个移位密码。凯撒密码加密解密。偏移12位就行。...

嵌入式开发-lin总线介绍 一.概述
1.1lin总线定义和历史 LIN总线(Local Interconnect Network)是一种基于UART/SCI(Universal Asynchronous Receiver-Transmitter/Serial Communication Interface)的低成本串行通信协议。它主要用于汽车、家电、办公设备等多种领域…...
羊城杯-2023-Crypto
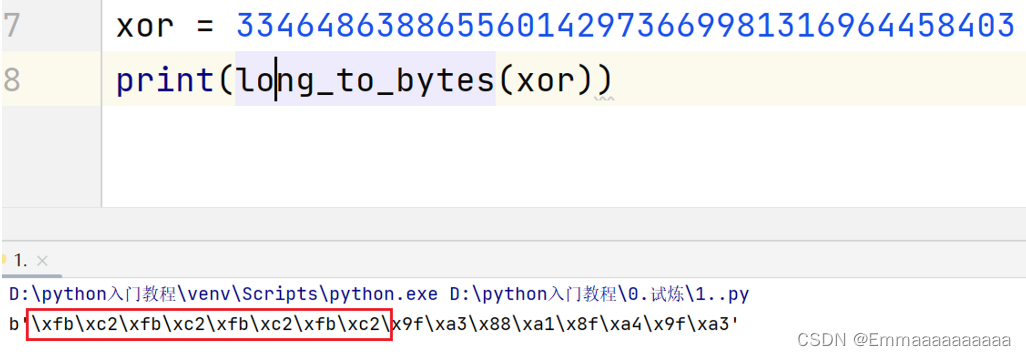
文章目录 Danger_RSA题目描述:题目分析: Easy_3L题目描述:题目分析: XOR贯穿始终题目描述:题目分析: MCeorpkpleer题目描述:题目分析: SigninCrypto题目描述:题目分析&am…...
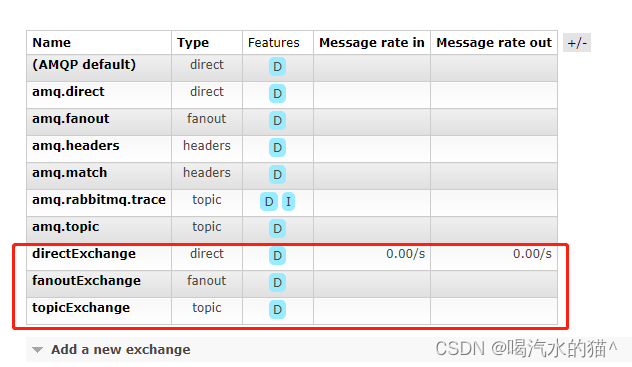
RabbitMQ快速上手及讲解
前言:在介绍RabbitMQ之前,我们先来看下面一个场景: 1.1.1.1 异步处理 场景说明: 用户注册后,需要发注册邮件和注册短信,传统的做法有两种 1.串行的方式 (1)串行方式:将注册信息写入数据库后&a…...
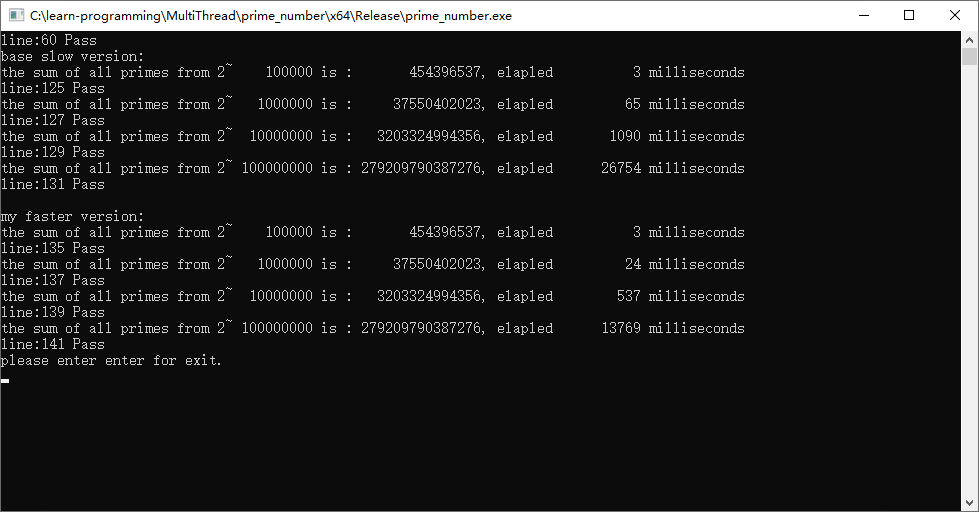
使用多线程std::thread发挥多核计算优势(解答)
使用多线程std::thread发挥多核计算优势(题目) 单核无能为力 如果我们的电脑只有一个核,那么我们没有什么更好的办法可以让我们的程序更快。 因为这个作业限制了你修改算法函数。你唯一能做的就是利用你电脑的多核。 使用多线程 由于我们…...
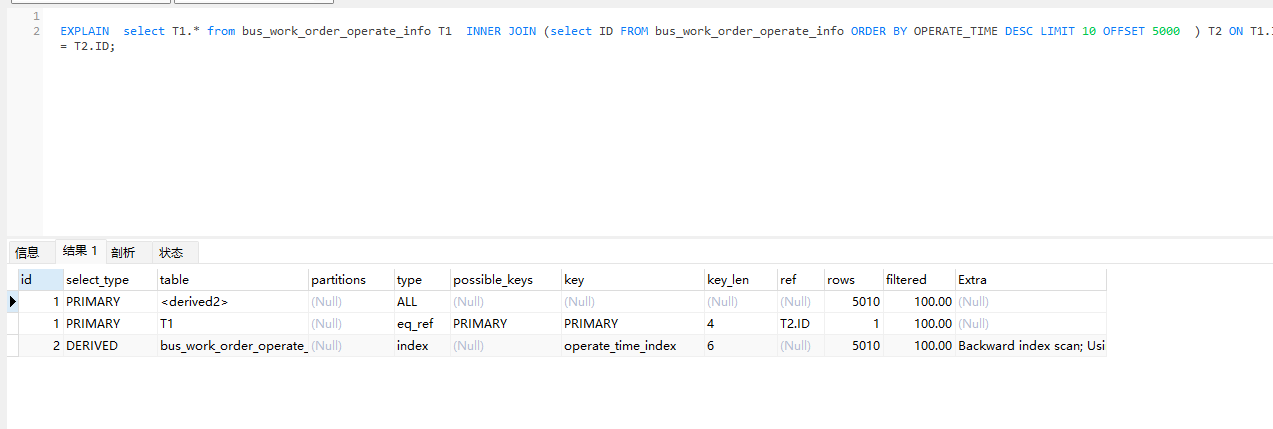
MySQL分页查询详解:优化大数据集的LIMIT和OFFSET
最近在工作中,我们遇到了一个需求,甲方要求直接从数据库导出一个业务模块中所有使用中的工单信息。为了实现这一目标,我编写了一条SQL查询语句,并请求DBA协助导出数据。尽管工单数量并不多,只有3000多条,但…...

解构赋值、函数默认值
暂时性死区,TDZ(Temporal Dead Zone) var x 1 {let x x//此处声明了x,但是没有对x赋值,相当于在赋值之前引用x,所以会造成报错console.log(x)//报错x is not defined,暂时性死区,…...

【已解决】Mybatis 实现 Group By 动态分组查询
🎉工作中遇到这样一个需求场景:实现一个统计查询,要求可以根据用户在前端界面筛选的字段进行动态地分组统计。也就是说,后端在实现分组查询的时候,Group By 的字段是不确定的,可能是一个字段、多个字段或者…...
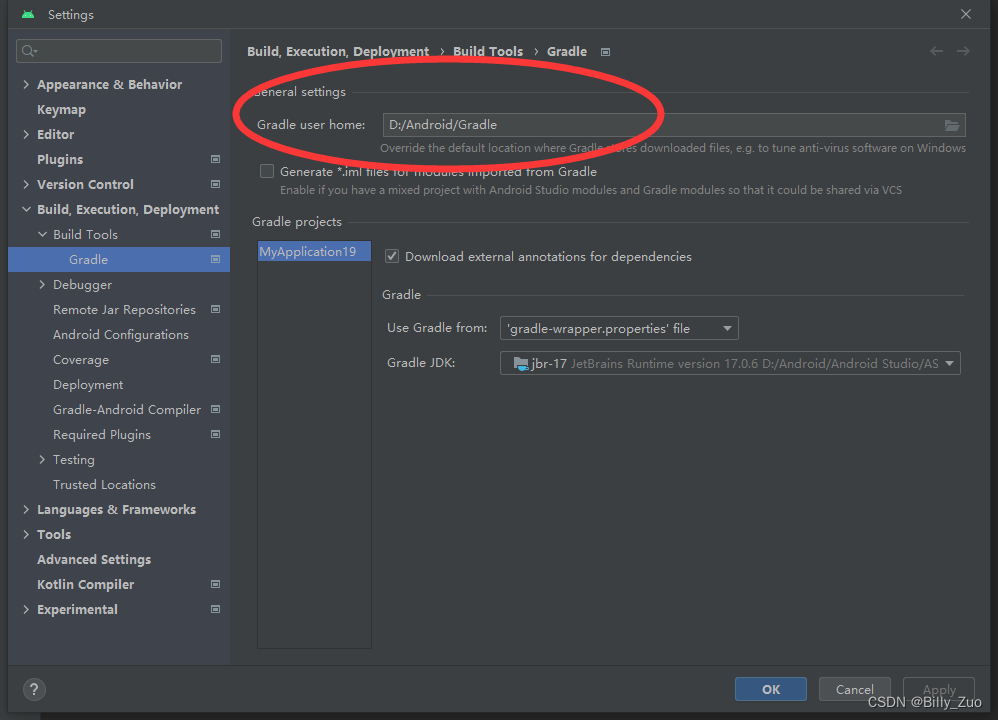
Android修改默认gradle路径
Android Studio每次新建项目,都会默认在C盘生成并下载gradle相关文件,由于C盘空间有限,没多久C盘就飘红了,于是就需要把gradle相关文件转移到其他盘 1、到C盘找到gradle文件 具体路径一般是:C:\Users\用户\ .gradle …...

原生JS+canvas实现炫酷背景
原生JScanvas实现炫酷背景 可以在需要的背景页使用 <!doctype html> <html> <head> <meta charset"utf-8"> <title>HTML5 Canvas矩阵粒子波浪背景动画特效</title> <style> html,body { height:100%; } body { …...
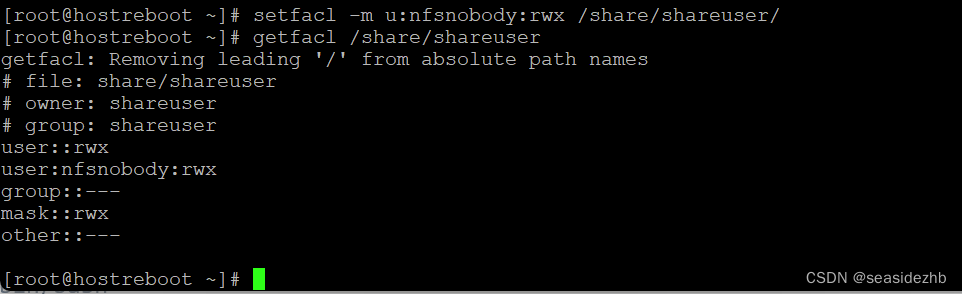
Linux学习之NAS服务器搭建
NAS是Network Attached Storage的缩写,也就是网络附属存储。可以使用自己已经不怎么使用的笔记本搭建一台NAS服务器。 fdisk -l可以看一下各个磁盘的状态。 可以看到有sda、sdb、sdc和sdd等四块硬盘。 lvs、vgs和pvs结合起来看,sdb和sdc没有被使用。 …...

分享码云上8个宝藏又有价值的开源图片编辑器
如果你需要高效地处理图片,那么这8款实用工具是可以尝试的! 它们能够进行一键抠图、放大、拼接、转矢量图、图标自动生成以及等操作,让你的工作效率飞升! 在Gitee这个最有价值的开源项目计划是Gitee综合评定出的优秀开源项目的展示…...

TCP Header都有啥?
分析&回答 源端口号(Source Port) :16位,标识主机上发起传送的应用程序; 目的端口(Destonation Port) :16位,标识主机上传送要到达的应用程序。 源端,目…...

无涯教程-Android - AutoCompleteTextView函数
AutoCompleteTextView是一个类似于EditText的视图,只是它在用户键入时自动显示补充数据。 AutoCompleteTextView - 属性 以下是与AutoCompleteTextView控件相关的重要属性。您可以查看Android官方文档以获取属性的完整列表以及可以在运行时更改这些属性的相关方法。…...

【Docker】 07-安装ElasticSearch、Kibana
安装ElasticSearch 1、拉取镜像 docker pull elasticsearch:6.4.2 2、运行 docker run -p 9200:9200 -p 9300:9300 --name es -d elasticsearch:6.4.2 启动会报错,按照下面流程修改 3、在宿主机中,修改配置sysctl.conf vim /etc/sysctl.conf 加入如下配…...
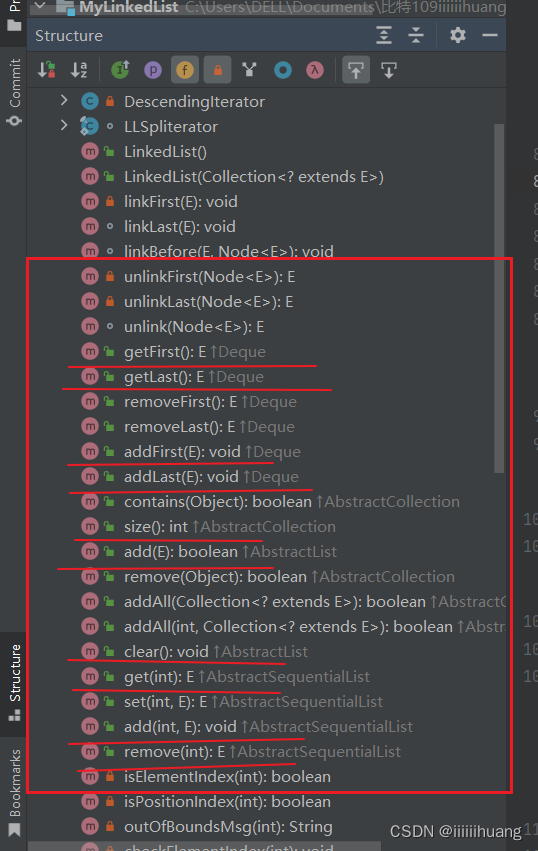
【数据结构篇】线性表1 --- 顺序表、链表 (万字详解!!)
前言:这篇博客我们重点讲 线性表中的顺序表、链表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列... 线性表在逻辑上是…...

C语言每日一练--Day(17)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。 今日练习题关键字:数对 截取字符串 💓博主csdn个人主页:小小unico…...
8月琐碎但值得的事情
8月份结束了,最近心态比较好,慢点就慢点,没有那么着急了,可能是因为着急也没啥办法, 8月是比较开心的一个月,可能是做的事情更有盼头了,可能是看了喜欢的书,可能是我变瘦了ÿ…...
苹果Mac系统如何优化流畅的运行?提高运行速度
Mac系统的稳定性和流畅性一直备受大家称赞,这也是大多数人选择Mac的原因,尽管如此,我们仍不时地对Mac进行优化、调整,以使其比以前更快、更流畅地运行。以下是小编分享给各位的Mac优化方法,记得保存哦~ 一、释放被过度…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
