代码随想录算法训练营第39天 | ● 62.不同路径 ● 63. 不同路径II
文章目录
- 前言
- 一、62.不同路径
- 二、63.不同路径II
- 总结
前言
动态规划
一、62.不同路径
- 深搜
- 动态规划
- 数论
深搜:
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:
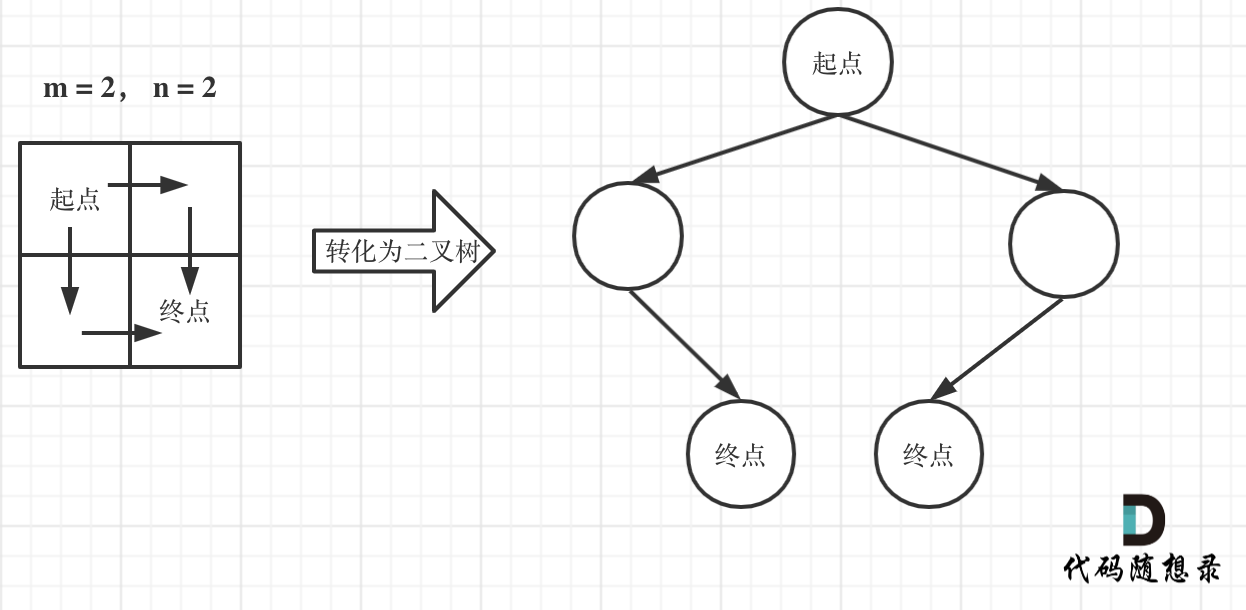
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
private:int dfs(int i, int j, int m, int n) {if (i > m || j > n) return 0; // 越界了if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);}
public:int uniquePaths(int m, int n) {return dfs(1, 1, m, n);}
};
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
动态规划:
- 定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
- dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
- 举例推导dp数组
如图所示:
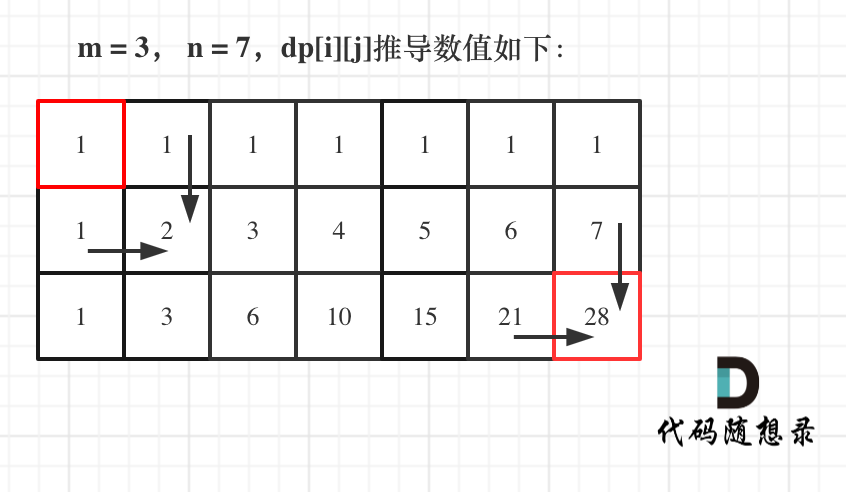
代码:
class Solution {public int uniquePaths(int m, int n) {int dp[][] = new int[m][n];for(int i = 0;i<m;i++){dp[i][0] = 1;}for(int j = 0;j<n;j++){dp[0][j] = 1;}for(int i = 1;i<m;i++){for(int j = 1;j<n;j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
}数论:
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
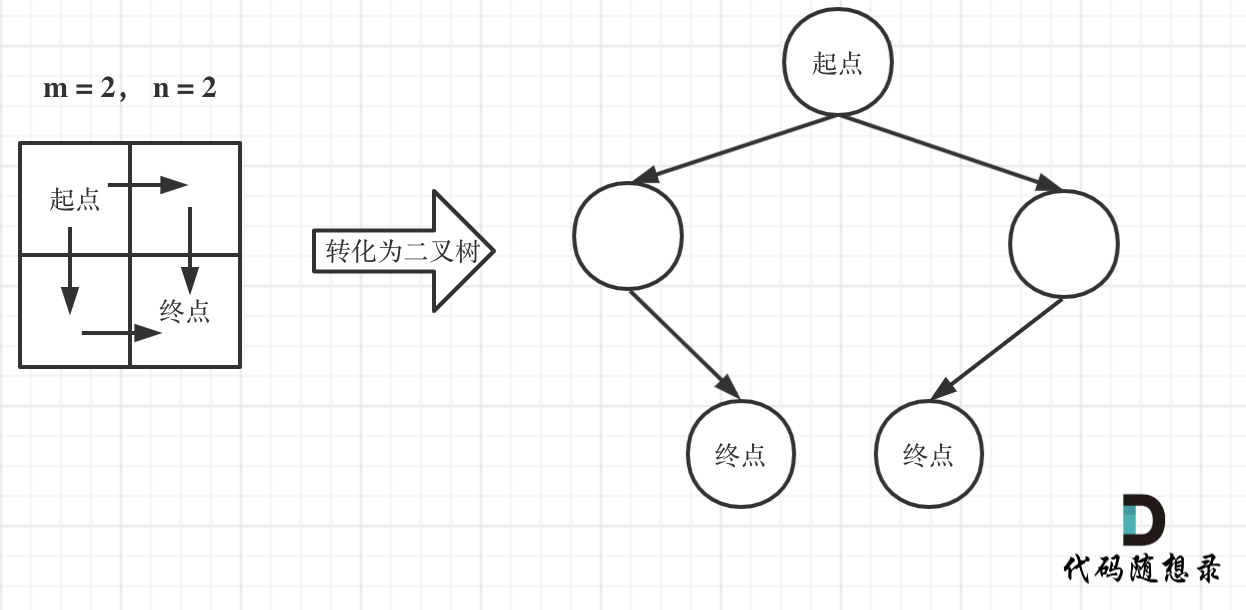
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。

求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; // 分子int denominator = m - 1; // 分母int count = m - 1;int t = m + n - 2;while (count--) {numerator *= (t--);while (denominator != 0 && numerator % denominator == 0) {numerator /= denominator;denominator--;}}return numerator;}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
二、63.不同路径II
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
在62.不同路径
(opens new window)不同路径中我们给出如下的初始化:
vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
如图:
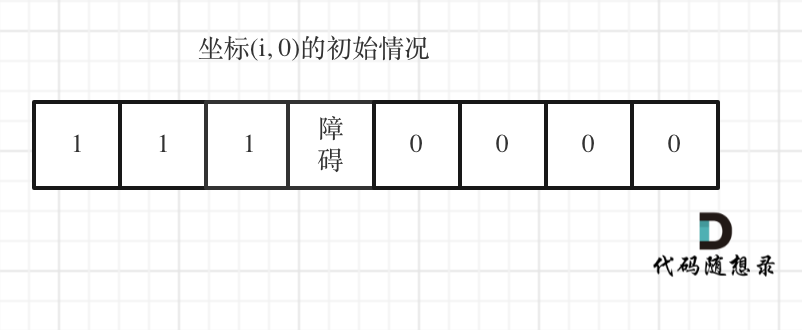
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
- 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}
}
- 举例推导dp数组
拿示例1来举例如题:
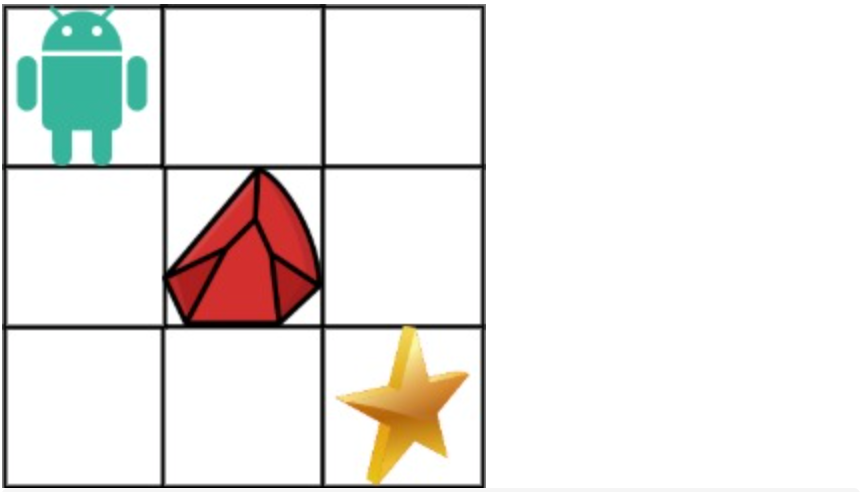
对应的dp table 如图:
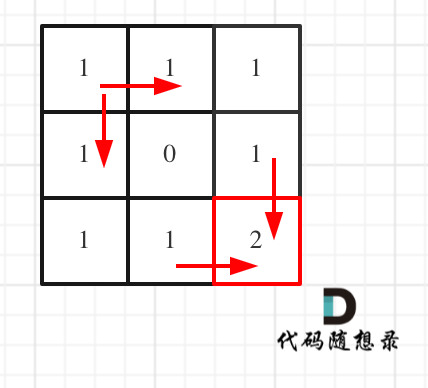
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int dp[][] = new int[m][n];if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1){return 0;}for(int i = 0;i<m && obstacleGrid[i][0] ==0;i++){dp[i][0] = 1;}for(int i = 0;i<n && obstacleGrid[0][i] ==0;i++){dp[0][i] = 1;}for(int i = 1;i<m;i++){for(int j =1;j<n;j++){if(obstacleGrid[i][j] ==0){dp[i][j] = dp[i-1][j] + dp[i][j-1];}else{dp[i][j] = 0;}}}return dp[m-1][n-1];}
}
总结
今天去看《奥本海默》。
相关文章:

代码随想录算法训练营第39天 | ● 62.不同路径 ● 63. 不同路径II
文章目录 前言一、62.不同路径二、63.不同路径II总结 前言 动态规划 一、62.不同路径 深搜动态规划数论 深搜: 注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点&#…...

《网站建设:从规划到发布的全过程详解》
一、引言 在数字时代,网站已经成为企业和个人在互联网上的重要存在。一个优质网站的建立需要周全的规划、设计、开发、测试和发布。本文将详细介绍网站建设的全过程,帮助读者了解和掌握网站建设的流程和方法。 二、网站建设的意义 网站建设具有以下意…...
1分钟实现 CLIP + Annoy + Gradio 文搜图+图搜图 系统
多模态图文搜索系统 CLIP 进行 Text 和 Image 的语义EmbeddingAnnoy 向量数据库实现树状结构索引来加速最近邻搜索Gradio 轻量级的机器学习 Web 前端搭建 文搜图 图搜图 CLIP图像语义提取功能!...

用树形dp+状压维护树上操作的计数问题:0902T3
发现操作数 k ≤ 6 k\le6 k≤6,可以考虑对操作进行状压。 然后找找性质,发现要么删掉一棵子树,要么进去该子树。可以视为每种操作有两种情况。 然后分讨一下当前该如何转移。 树形dp的顺序: 合并子树考虑当前往上的边的方向 …...
【python爬虫】批量识别pdf中的英文,自动翻译成中文上
不管是上学还是上班,有时不可避免需要看英文文章,特别是在写毕业论文的时候。比较头疼的是把专业性很强的英文pdf文章翻译成中文。我记得我上学的时候,是一段一段复制,或者碰到不认识的单词就百度翻译一下,非常耗费时间。本文提供批量识别pdf中英文的方法,后续文章实现自…...

Android笔记--Hilt
Hilt 是 Android 的依赖项注入库,可减少在项目中执行手动依赖项注入的样板代码。执行手动依赖项注入要求您手动构造每个类及其依赖项,并借助容器重复使用和管理依赖项。依赖注入的英文是Dependency Injection,简称DI,简单说一个类中使用的依赖…...

Oracle常用权限处理
对于Oracle来说,用户等于Schema,创建用户即创建Schema -- 创建用户 create user TCK_TEXT identified by "TCKTCK"; --赋予登陆权限 grant connect to TCK_TEXT; --查看权限列表 select * from user_role_privs ; select * from user_sys_priv…...
Stable Diffuse 之 本地环境部署 WebUI 进行汉化操作
Stable Diffuse 之 本地环境部署 WebUI 进行汉化操作 目录 Stable Diffuse 之 本地环境部署 WebUI 进行汉化操作 一、简单介绍 二、汉化操作 附录: 一、Install from URL 中出现 Failed to connect to 127.0.0.1 port 7890: Connection refused 错误…...

r 安装源码包 安装本地r包
总结一下手动安装R包 - 简书 (jianshu.com)https://www.jianshu.com/p/2a7a36414734 #BiocManager::install("simplifyEnrichment") #BiocManager::install("EnsDb.Hsapiens.v86")#下载包 之后 手动安装 #install.packages("~/datasets/EnsDb.Hsapien…...
webservice调用对接第三方系统
#webservice调用对接第三方系统# 最近接到一个任务,需要对接第三方数据,第三方提供对接方式的是通过webservice调用,webservice调用有好几种方式,具体可以自行了解,我选择的是通过wsdl文件自动生成客户端代码对接。 …...
实现不同局域网文件共享的解决方案:使用Python自带HTTP服务和端口映射
文章目录 1. 前言2. 本地文件服务器搭建2.1 python的安装和设置2.2 cpolar的安装和注册 3. 本地文件服务器的发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 数据共享作为和连接作为互联网的基础应用,不仅在商业和办公场景有广泛的应用…...

[Android 四大组件] --- Activity
1 Activity是什么 Activity是一个Android的应用组件,它提供屏幕进行交互。每个Activity都会获得一个用于绘制其用户界面的窗口,窗口可以充满哦屏幕也可以小于屏幕并浮动在其他窗口之上。 一个应用通常是由多个彼此松散联系的Activity组成&…...

shell中for循环输出1-6
介绍单for循环的语法,以及对数字的循环使用 1、语法介绍 for 变量 in 值列表 do #执行的命令或代码块 Done其中,变量是用来存放每个值的变量名,值列表是需要遍历值的集合,在每次循环中,变量会被设置为值列表中的一…...

docker 04.更加重要的命令
之前的都是基础命令, 前台交互进程和后台守护进程: 重新进入容器: docker中的导入导出: docker中的拷贝到:...
线性运算和线性空间)
【理解线性代数】(二)线性运算和线性空间
1. 从112看线性运算 11为什么等于2?其实11等于2有一个前提条件,那就是必须在线性运算规则下进行。什么是线性运算规则呢? 理解起来很简单,在一条直线上, 一米的直线长度一米的直线长度两米的直线长度 两个数相加的结…...

专业的视觉特效处理包,FxFactory 8 Pro for Mac助您打造精彩视频
FxFactory 8 Pro for Mac是一款强大的视觉特效处理包,专门为Mac用户设计。它集成了超过200种高质量的视觉效果和过渡效果,可以轻松地应用于各种视频项目中。该软件提供了一个直观的界面,用户可以通过简单拖放操作将特效应用到视频片段上。它支…...
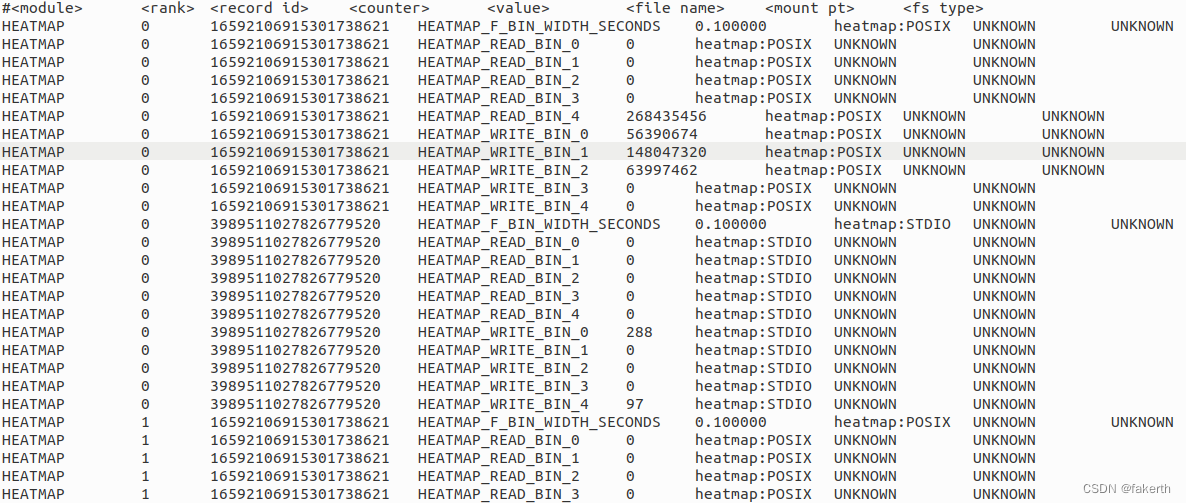
Darshan日志分析
标头 darshan-parser 输出的开头显示了有关作业的总体信息的摘要。还可以使用–perf、–file或–total命令行选项生成其他作业级别摘要信息。 darshan log version:Darshan 日志文件的内部版本号。compression method:压缩方法。exe:生成日志…...

python中如何不修改字符串的前提,使其对大小写字母不敏感
如果你希望在不修改原字符串的基础上实现大小写不敏感的比较,你可以使用内置函数str.casefold(),它会将字符串转换为小写并处理一些特殊字符,使得比较更加严格。下面是如何使用它来实现大小写不敏感的比较: x input() y input()…...

聊聊Http服务化改造实践
在微服务架构体系中远程RPC调用主要包括Dubbo与Http调用两个大类,由于Dubbo拥有服务注册中心,并且起服务的命名非常规范,使用包名.类名.方法名进行描述。 而http调用通常都是使用httpclient等相关类库,这些在使用上并没有问题&am…...

docker打包部署
打包成容器命令 docker build -f ./Dockerfile-long -t 名称.打包镜像 tar docker save -o 名称.tar 名称:latest执行sudo -i,提示输入用户密码,输入密码后进入超级用户(root)模式 linux上传文件 rz -ytar恢复成镜像 sudo docker…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
