C语言关于与运算符
C语言关于&与&&运算符
我们知道,在很多场景中&和&&通常可以相互代替,那么它们到底有什么不同呢?
先看一段代码
bool a, b, c;
c = a & b;
使用clang++ -S编译出来的指令如下:
movb -5(%rbp), %al # aandb $1, %almovzbl %al, %eaxmovb -6(%rbp), %cl # bandb $1, %clmovzbl %cl, %ecxandl %ecx, %eax # a & bcmpl $0, %eaxsetne %alandb $1, %al movb %al, -7(%rbp) # c
使用clang++ -S -O3编译出来的指令如下:
movzbl -1(%rbp), %edxandb -2(%rbp), %dl
再看一段代码:
bool a, b, c;
c = a && b;
其汇编代码为:
xorl %eax, %eaxtestb $1, -5(%rbp) # amovb %al, -8(%rbp) je .LBB2_2
# %bb.1:movb -6(%rbp), %al # bmovb %al, -8(%rbp)
.LBB2_2:movb -8(%rbp), %al andb $1, %almovb %al, -7(%rbp) # c
反汇编一下:
tmp = a;
if(a==1) {tmp = b;
}
c = tmp & 1;
通过对比两段汇编代码就很清晰了,&运算在底层表现为一条指令and,而&&运算实际上需要通过分支的方式实现。
那么能否说明&的效率比&&要高呢?不一定
我们知道,&是与运算,例如要得到a & b的值,就必须分别求得a和b的值。但是&&通过分支的方式实现,要想得到a && b的值,其实不必都求出a和b的值,如果先求出a的值是0,那么就不必再求b了。
再看一段代码:
bool funcA() {}bool funcB() {}int main () {bool c = funcA() & funcB();bool d = funcA() && funcB();
}
上述代码中表达式funcA() & funcB() 与 funcA() && funcB() 哪一个效率更高?
需要具体分析funcA()和funcB()的返回值分布与复杂度,如果funcA()和funcB()复杂度很低,并且大部分情况下返回1,那么funcA() & funcB()的效率可能会高些;如果funcA()和funcB()复杂度较高,并且有可能返回0,那么funcA() && funcB()会高一些。
另外值得一提的是,funcA() && funcB()与funcB() && funcA()哪个效率高?
| 返回0概率 | 复杂性(耗时) | |
|---|---|---|
| funcA() | a_pz | a_cost |
| funcB() | b_pz | b_cost |
funcA() && funcB() 期望耗时为:
a_cost + (1-a_pz) * b_cost
funcB() && funcA() 期望耗时为:
b_cost + (1-b_pz) * a_cost
举个例子
| 返回0概率 | 复杂性(耗时) | |
|---|---|---|
| funcA() | 0.9 | 50 |
| funcB() | 0.8 | 40 |
funcA() && funcB() 期望耗时为54; funcB() && funcA() 期望耗时为50
相关文章:

C语言关于与运算符
C语言关于&与&&运算符 我们知道,在很多场景中&和&&通常可以相互代替,那么它们到底有什么不同呢? 先看一段代码 bool a, b, c; c a & b;使用clang -S编译出来的指令如下: movb -5(%rbp), %al …...

计算机网络(速率、宽带、吞吐量、时延、发送时延)
速率: 最重要的一个性能指标。 指的是数据的传送速率,也称为数据率 (data rate) 或比特率 (bit rate)。 单位:bit/s,或 kbit/s、Mbit/s、 Gbit/s 等。 例如 4 1010 bit/s 的数据率就记为 40 Gbit/s。 速率往往是指额定速率或…...

kubectl入门
一.kubectl的三种资源管理方式: 二. kubectl资源介绍: 1.namespace:实现多套环境的资源隔离或者多租户的资源隔离。k8s中的pod默认可以相互访问,如果不想让两个pod之间相互访问,就将其划分到不同ns下。 2.podÿ…...
Android JNI系列详解之ndk-build工具的使用
一、Android项目中使用ndk-build工具编译库文件 之前介绍过CMake编译工具的使用,今天介绍一种ndk自带的编译工具ndk-build的使用。 ndk-build目前主要有两种配置使用方式: 如上图所示,第一种方式是Android.mkApplication.mkgradle的方式生成…...
【业务功能篇90】微服务-springcloud-检索服务-ElasticSearch实战运用-DSL语句
商城检索服务 1.检索页面的搭建 商品检索页面我们放在search服务中处理,首页我们需要在mall-search服务中支持Thymeleaf。添加对应的依赖 <!-- 添加Thymeleaf的依赖 --><dependency><groupId>org.springframework.boot</groupId><artifa…...

QTday4
实现闹钟功能 1》 头文件 #ifndef BURGER_H #define BURGER_H#include <QWidget> #include <QLabel> #include <QLineEdit> #include <QPushButton> #include <QTextEdit> #include <QTimerEvent> //定时器事件类 #include <QDateTim…...

设计模式之命令模式(Command)的C++实现
1、命令模式的提出 在软件开发过程中,“行为请求者”和“行为实现者”通常呈现一种“紧耦合”,如果行为的实现经常变化,则不利于代码的维护。命令模式可以将行为的请求者和行为的实现者进行解耦。具体流程是将行为请求者封装成一个对象&…...
取证工具prodiscover的基本操作
前言提醒 取证工具ProDiscover在网上讲解操作的文章实在太少,一是prodiscover是用于磁盘取证的工具,本身比较小众比不上其他的编程软件能用到的地方多,二是这个工具是用来恢复提取磁盘中被删除的文件,是比较隐晦的软件。 需要注…...
flutter plugins插件【二】【FlutterAssetsGenerator】
2、FlutterAssetsGenerator 介绍地址:https://juejin.cn/post/6898542896274735117 配置assets目录 插件会从pubspec.yaml文件下读取assets目录,因此要使用本插件,你需要在pubspec.yaml下配置资源目录 flutter:# The following line ens…...

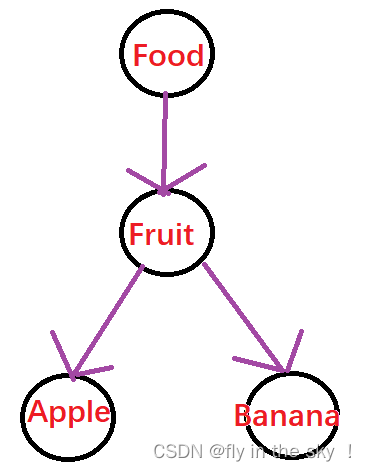
看懂UML类图
UML 统一建模语言(Unified Modeling Language,UML)是一种为面向对象系统的产品进行说明、可视化和编制文档的一种标准语言,是非专利的第三代建模和规约语言。UML是面向对象设计的建模工具,独立于任何具体程序设计语言。 类的表示 首先看那个…...
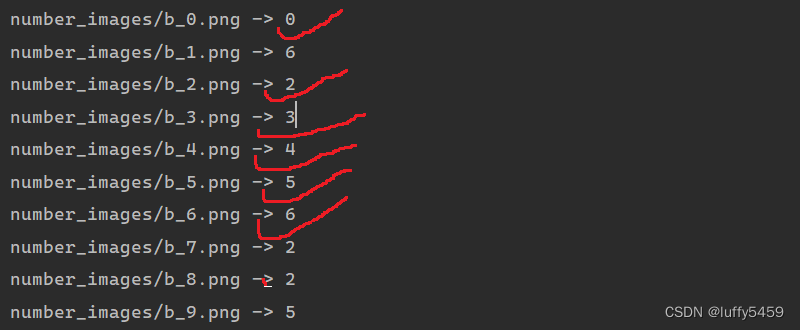
keras深度学习框架通过简单神经网络实现手写数字识别
背景 keras深度学习框架,并不是一个独立的深度学习框架,它后台依赖tensorflow或者theano。大部分开发者应该使用的是tensorflow。keras可以很方便的像搭积木一样根据模型搭出我们需要的神经网络,然后进行编译,训练,测试…...

React 中的 ref 如何操作 dom节点,使输入框获取焦点
聚焦文字输入框 .focus() 获取焦点 当用户点击按钮时,handleClick 函数会被调用,从而将焦点聚焦到文本输入框上。 // 焦文字输入框 import { useRef } from "react";const FocusForm () > {const inputRef useRef<any>(null);func…...

最短路Dijkstra,spfa,图论二分图算法AYIT---ACM训练(模板版)
文章目录 前言A - Dijkstra Algorithm0x00 算法题目0x01 算法思路0x02 代码实现 B - 最长路0x00 算法题目0x01 算法思路0x02 代码实现 C - 二分图最大匹配0x00 算法题目0x01 算法思路0x02 代码实现 D - 搭配飞行员0x00 算法题目0x01 算法思路0x02 代码实现 E - The Perfect Sta…...

AK 微众银行 9.3 笔试 Java后端方向
T1(模拟,二分) (没看清买的糖果只有前缀,一开始用二分写了,后来意识到也没改了,简单写的话,直接模拟就好了) #include <bits/stdc.h>#define endl \nusing namespace std;const int N 50010;int n; int a[N];bool check(…...
了解java中的通配符“?“
目录 通配符的作用 先看一段代码 用通配符"?"后,代码变化 结论 通配符上界 通配符下界 对通配符上下界的注释理解及其练习代码 简记: ? 用于在泛型的使用,即为通配符. 在Java中,通配符(wildcard)主要用于泛型…...

浙大陈越何钦铭数据结构07-图6 旅游规划【最小堆实现】
题目: 题目和浙大陈越何钦铭数据结构07-图6 旅游规划是一样的,不同的是用最小堆实现函数【FindMinDist】。 时间复杂度对比: 浙大陈越何钦铭数据结构07-图6 旅游规划: 创建图(CreateGraph):时…...
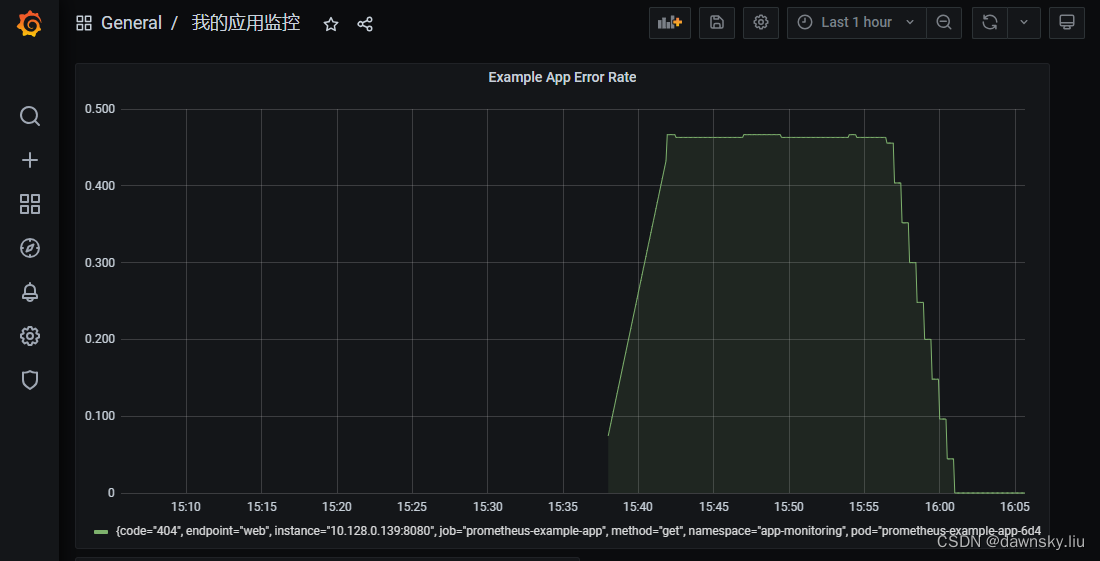
OpenShift 4 - 用 Prometheus 和 Grafana 监视用户应用定制的观测指标(视频)
《OpenShift / RHEL / DevSecOps 汇总目录》 说明:本文已经在 OpenShift 4.13 的环境中验证 文章目录 OpenShift 的监控功能构成部署被监控应用用 OpenShift 内置功能监控应用用 Grafana 监控应用安装 Grafana 运行环境配置 Grafana 数据源定制监控 Dashboard 演示视…...
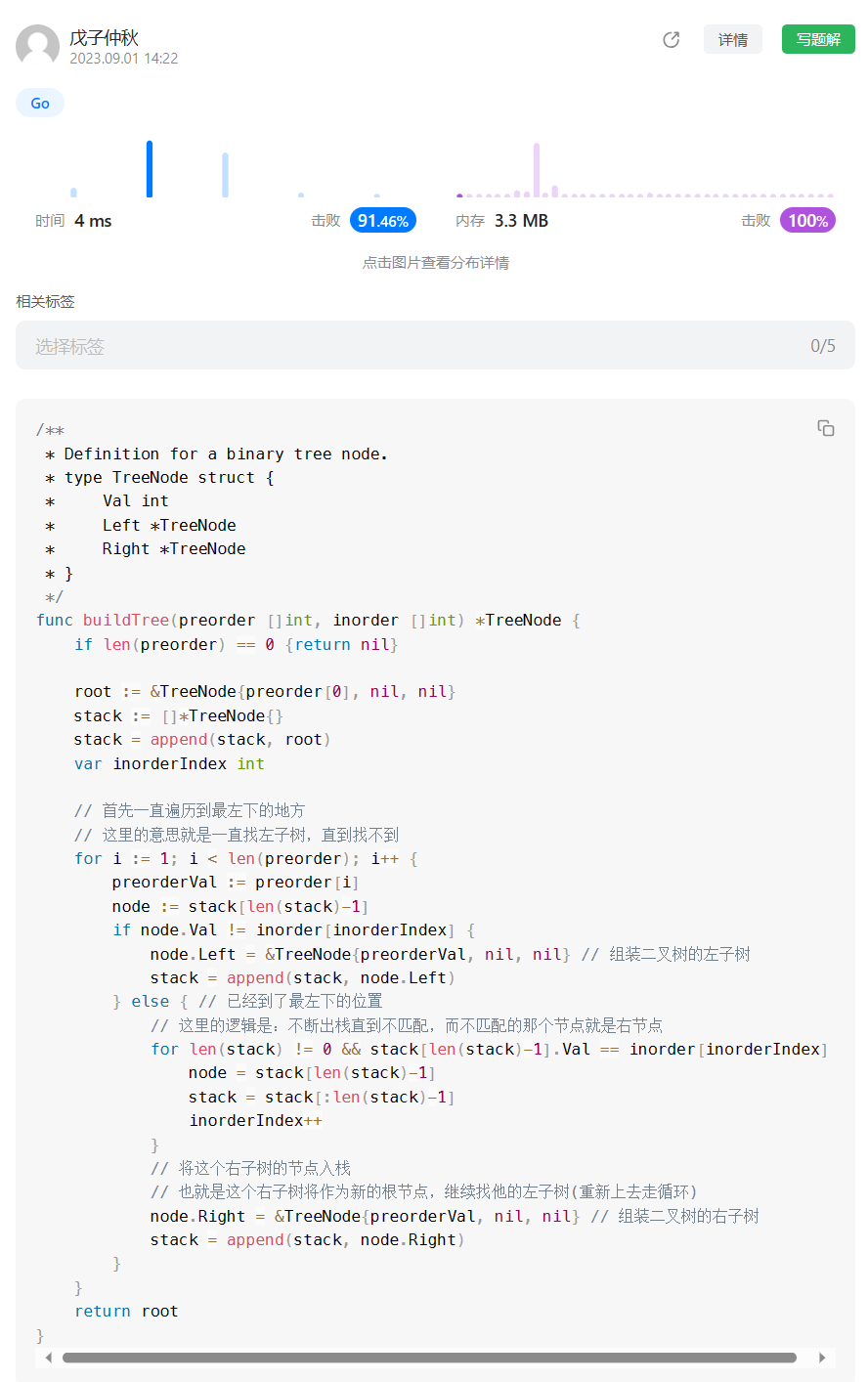
【LeetCode】剑指 Offer <二刷>(3)
目录 题目:剑指 Offer 06. 从尾到头打印链表 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 07. 重建二叉树 - 力扣…...

Ceph IO流程及数据分布
1. Ceph IO流程及数据分布 1.1 正常IO流程图 步骤: client 创建cluster handler。client 读取配置文件。client 连接上monitor,获取集群map信息。client 读写io 根据crshmap 算法请求对应的主osd数据节点。主osd数据节点同时写入另外两个副本节点数据。…...

Netty-NIO
文章目录 一、NIO-Selector1.处理accept2.cancel3.处理read4.处理客户端断开5. 处理消息的边界6. 写入内容过多的问题7. 处理可写事件 一、NIO-Selector 1.处理accept //1.创建selector,管理多个channel Selector selector Selector.open(); ByteBuffer buffer ByteBuffer.…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
