直方图反向投影(Histogram Backprojection)
直方图反向投影(Histogram Backprojection)是一种在计算机视觉中用于对象检测和图像分割的技术。它的原理基于图像的颜色分布,允许我们在一幅图像中找到与给定对象颜色分布相匹配的区域。这个技术常常用于图像中的目标跟踪、物体识别和图像分割等任务。
原理:
直方图反向投影的原理基于以下概念:我们首先要建立一个“目标颜色模型”的直方图,该直方图描述了我们希望检测的对象的颜色分布。然后,我们将这个目标颜色模型与输入图像进行比较,为输入图像的每个像素分配一个分数,以表示该像素属于目标对象的可能性。得分较高的像素被认为更可能属于目标对象。
数学公式:
直方图反向投影的数学公式如下:
backProj ( x , y ) = histModel ( I ( x , y ) ) \text{backProj}(x,y) = \text{histModel}(I(x,y)) backProj(x,y)=histModel(I(x,y))
其中:
- backProj ( x , y ) \text{backProj}(x, y) backProj(x,y) 表示在坐标 ( x , y ) (x, y) (x,y)处的反向投影值。
- histModel \text{histModel} histModel 是目标颜色模型的直方图。
- I ( x , y ) I(x, y) I(x,y) 表示输入图像中的像素值。
适用场景:
直方图反向投影适用于需要根据对象的颜色分布来检测和分割目标的情况。例如,在图像中寻找具有特定颜色或颜色分布的对象,或者用于跟踪运动对象时,可以使用直方图反向投影来提高目标检测的精确性。
以下是使用Python的OpenCV库进行直方图反向投影的示例代码:
import cv2
import numpy as np
import matplotlib.pyplot as pltdef Histogram_Backprojection(image):img=cv2.imread(image)if img is None:print('Unable to load image!')else:# 定义目标对象的区域(在这个例子中,我们使用一个矩形区域)(x1,y1)=(60,30)(x2,y2)=(120,60)roi=img[y1:y2,x1:x2]# 将目标对象的颜色模型转换为HSV颜色空间roi_hsv=cv2.cvtColor(roi,cv2.COLOR_BGR2HSV)# 计算目标对象的颜色直方图hist = cv2.calcHist([roi_hsv], [0, 1], None, [180, 256], [0, 180, 0, 256])# 归一化直方图cv2.normalize(hist, hist, 0, 255, cv2.NORM_MINMAX)# 计算图像的反向投影backProj = cv2.calcBackProject([img], [0, 1], hist, [0, 180, 0, 256], 1)plt.figure(figsize=(6, 4))plt.subplot(121), plt.title('Original image'), plt.axis('off')plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))plt.subplot(122), plt.title('backProj image'), plt.axis('off')plt.imshow(cv2.cvtColor(backProj, cv2.COLOR_BGR2RGB))plt.tight_layout()plt.show()
imgfile1='./Images/cat.jpg'
Histogram_Backprojection(imgfile1)
在这个示例中,我们首先从输入图像中选择了一个感兴趣的区域(ROI),然后将其转换为HSV颜色空间。接下来,计算了目标对象的颜色直方图,并将其归一化。最后,使用cv2.calcBackProject函数计算了输入图像的反向投影,以显示目标对象可能存在的区域。
相关文章:
)
直方图反向投影(Histogram Backprojection)
直方图反向投影(Histogram Backprojection)是一种在计算机视觉中用于对象检测和图像分割的技术。它的原理基于图像的颜色分布,允许我们在一幅图像中找到与给定对象颜色分布相匹配的区域。这个技术常常用于图像中的目标跟踪、物体识别和图像分…...

day32 泛型 数据结构 List
一、泛型 概述 JDK1.5同时推出了两个和集合相关的特性:增强for循环,泛型 泛型可以修饰泛型类中的属性,方法返回值,方法参数, 构造函数的参数 Java提供的泛型类/接口 Collection, List, Set,Iterator 等 …...

DW-AHB Central DMAC
文章目录 AHB Central DMAC —— Design Ware AHB Central DMAC —— Design Ware AHB(Adavenced High-performace BUS) Central DMAC(Direct Memory Access Controller) : 一个高性能总线系统。 作用:在嵌入式系统种连接高速设备,如处理器内存&#x…...

JavaScript设计模式(四)——策略模式、代理模式、观察者模式
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

JS画布的基本使用
直线 <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title></title> <style> #myname{ border: 1px solid red; /* background: linear-gradient(to righ…...

c++ set/multiset
set/multiset 集合,一个单个,一个多个(multi)。两个库都是"set"。 https://blog.csdn.net/fckbb/article/details/130917681 对象创建 set(const Pred& compPred(),const A& alA()):创建空集合。set(const set& x):…...
)
多线程与高并发——并发编程(4)
文章目录 四、阻塞队列1 基础概念1.1 生产者消费者概念1.2 JUC阻塞队列的存取方法2 ArrayBlockingQueue2.1 ArrayBlockingQueue的基本使用2.2 生产者方法实现原理2.2.1 ArrayBlockingQueue的常见属性2.2.2 add方法2.2.3 offer方法2.2.4 offer(time,unit)方法2.2.5 put方法2.3 消…...
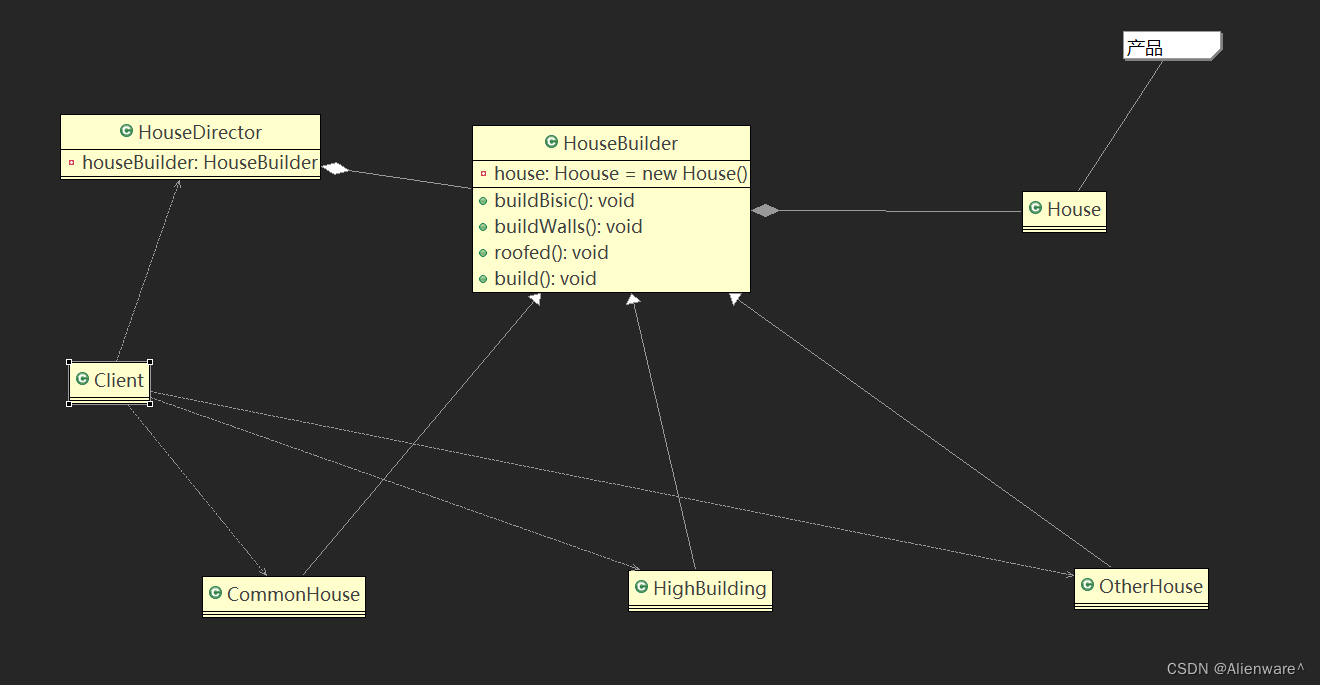
设计模式之建造者模式
文章目录 盖房项目需求传统方式解决盖房需求传统方式的问题分析建造者模式概述是建造者模式的四个角色建造者模式原理类图建造者模式的注意事项和细节 盖房项目需求 需要建房子:这一过程为打桩、砌墙、封顶房子有各种各样的,比如普通房,高楼…...

源码编译安装opencv4.6.0,别的版本也行
1.下载opencv4.6.0 系统: ubuntu 1804 64位点我下载opencv 4.6.0 https://codeload.github.com/opencv/opencv/zip/refs/tags/4.6.0 指令下载 推荐: wget -O opencv.zip https://github.com/opencv/opencv/archive/4.6.0.zip wget -O opencv_contrib.zip https://github.com/…...

【MongoDB】Springboot中MongoDB简单使用
1. docker安装MongoDB 拉取镜像 docker pull mongo创建容器 docker run -di --name mongo-service --restartalways -p 27017:27017 -v ~/data/mongodata:/data mongo2. 导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactI…...

Python 面试:单元测试unit testing 使用pytest
1. 对于函数进行单元测试 calc.py def add(x, y):"""Add Function"""return x ydef subtract(x, y):"""Subtract Function"""return x - ydef multiply(x, y):"""Multiply Function""…...

螺旋矩阵、旋转矩阵、矩阵Z字打印
螺旋矩阵 #include <iostream> #include <vector> void display(std::vector<std::vector<int>>&nums){for(int i 0; i < nums.size(); i){for(int j 0; j < nums[0].size(); j){std::cout<<nums[i][j]<< ;}std::cout<<…...
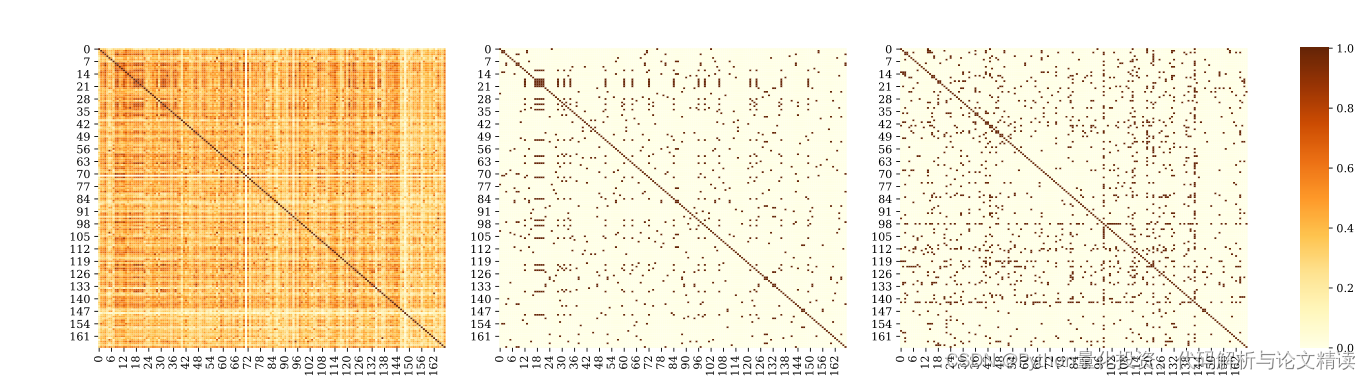
Seaborn绘制热力图的子图
Seaborn绘制热力图的子图 提示:如何绘制三张子图 绘制的时候,会出现如下问题 (1)如何绘制1*3的子图 (2)三个显示条,如何只显示最后一个 提示:下面就展示详细步骤 Seaborn绘制热力…...

C++二级题目4
小白鼠再排队 不会 多余的数 #include<iostream> #include<string.h> #include<stdio.h> #include<iomanip> #include<cmath> #include<bits/stdc.h> int a[2000][2000]; int b[2000]; char c[2000]; long long n; using namespace std; i…...
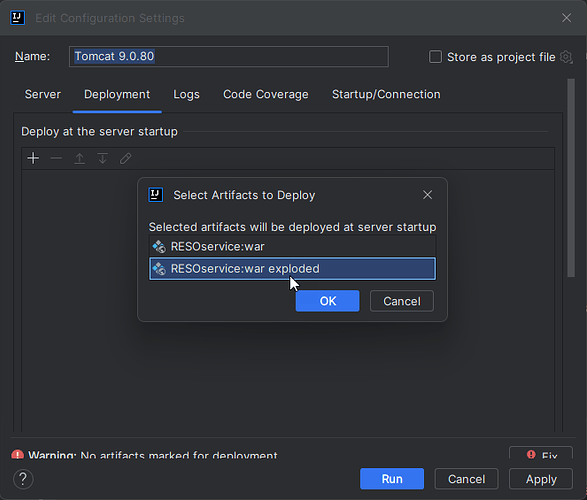
Tomcat 部署时 war 和 war exploded区别
在 Tomcat 调试部署的时候,我们通常会看到有下面 2 个选项。 是选择war还是war exploded 这里首先看一下他们两个的区别: war 模式:将WEB工程以包的形式上传到服务器 ;war exploded 模式:将WEB工程以当前文件夹的位置…...

Delphi IdTcpServer IdTcpClient 传输简单文本
Delphi IdTcpServer IdTcpClient 传输简单文本 已经很久敲代码了,想找一段直接Delphi11 TCP简单文本传输,费劲!FStringStream 、FStrStream : FStringStream:TStringStream.Create(,TEncoding.UTF8); 已经很久敲代码了,…...
界面控件Telerik UI for WPF——Windows 11主题精简模式提升应用体验
Telerik UI for WPF拥有超过100个控件来创建美观、高性能的桌面应用程序,同时还能快速构建企业级办公WPF应用程序。Telerik UI for WPF支持MVVM、触摸等,创建的应用程序可靠且结构良好,非常容易维护,其直观的API将无缝地集成Visua…...

PoseC3D 基于人体姿态的动作识别新范式
摘要1. Introduction2. Related Work动作识别 3D-CNN基于骨架的动作识别 GCN基于骨骼的动作识别 2D-CNN3. Framework3.1. Good Practice for Pose Extraction3.2. From 2D Poses to 3D Heatmap Volumes3.3 基于骨骼的动作识别 3D-CNNPose-SlowOnlyRGBPose-SlowFast4. Experimen…...

html2canvas 截图空白 或出现toDataURL‘ on ‘HTMLCanvasElement或img标签没截下来 的所有解决办法
1.如果截图空白: 1.1以下的参数是必须要有的。 width: shareContent.offsetWidth, //设置canvas尺寸与所截图尺寸相同,防止白边height: shareContent.offsetHeight, //防止白边logging: true,useCORS: true,x:0,y:0,2,如果出现了报错 toData…...

Eclipse错误提示: Symbol ‘xxxx‘ could not be resolved
问题现象: 调试FPGA时,如果在qsys中增加新的内容,到nios中编译的时候就会提示找不到宏定义。 而这些宏定义都是在system.h这个头文件中的,原来的宏定义都能找到,就是新增的找不到,这个应该和头文件路径没有…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
