机器学习和数据挖掘04-PowerTransformer与 MinMaxScaler
概念 PowerTransformer(幂变换器)
PowerTransformer 是用于对数据进行幂变换(也称为Box-Cox变换)的预处理工具。幂变换可以使数据更接近正态分布,这有助于某些机器学习算法的性能提升。它支持两种常用的幂变换:Yeo-Johnson变换和Box-Cox变换。
代码实现
from sklearn.preprocessing import PowerTransformer
import numpy as npdata = np.array([[1.0], [2.0], [3.0], [4.0], [5.0]])transformer = PowerTransformer(method='yeo-johnson')
transformed_data = transformer.fit_transform(data)print("Original Data:\n", data)
print("Transformed Data:\n", transformed_data)概念MinMaxScaler(最小-最大缩放器)
MinMaxScaler 是用于将数据进行最小-最大缩放的预处理工具。它将数据缩放到指定的范围,通常是
0,到。这对于那些受到特征尺度影响的算法(如K近邻和支持向量机)非常有用。
代码实现
from sklearn.preprocessing import MinMaxScaler
import numpy as npdata = np.array([[1.0], [2.0], [3.0], [4.0], [5.0]])scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(data)print("Original Data:\n", data)
print("Scaled Data:\n", scaled_data)相关文章:

机器学习和数据挖掘04-PowerTransformer与 MinMaxScaler
概念 PowerTransformer(幂变换器) PowerTransformer 是用于对数据进行幂变换(也称为Box-Cox变换)的预处理工具。幂变换可以使数据更接近正态分布,这有助于某些机器学习算法的性能提升。它支持两种常用的幂变换&#x…...
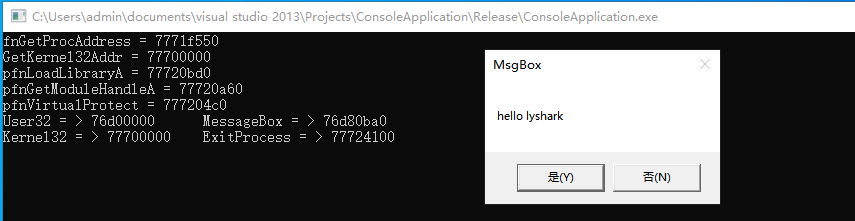
1.15 自实现GetProcAddress
在正常情况下,要想使用GetProcAddress函数,需要首先调用LoadLibraryA函数获取到kernel32.dll动态链接库的内存地址,接着在调用GetProcAddress函数时传入模块基址以及模块中函数名即可动态获取到特定函数的内存地址,但在有时这个函…...

总结ADX指标交易的好处
股神巴菲特从一个穷小子变成世界富豪,而闻名世界。anzo capital昂首资本以为这辈子再也不会和巴菲特产生任何交集,直到我看了巴菲特的发家史,才发现原来我们都使用过ADX指标盈利过,下面anzo capital昂首资本就总结一下使用ADX指…...
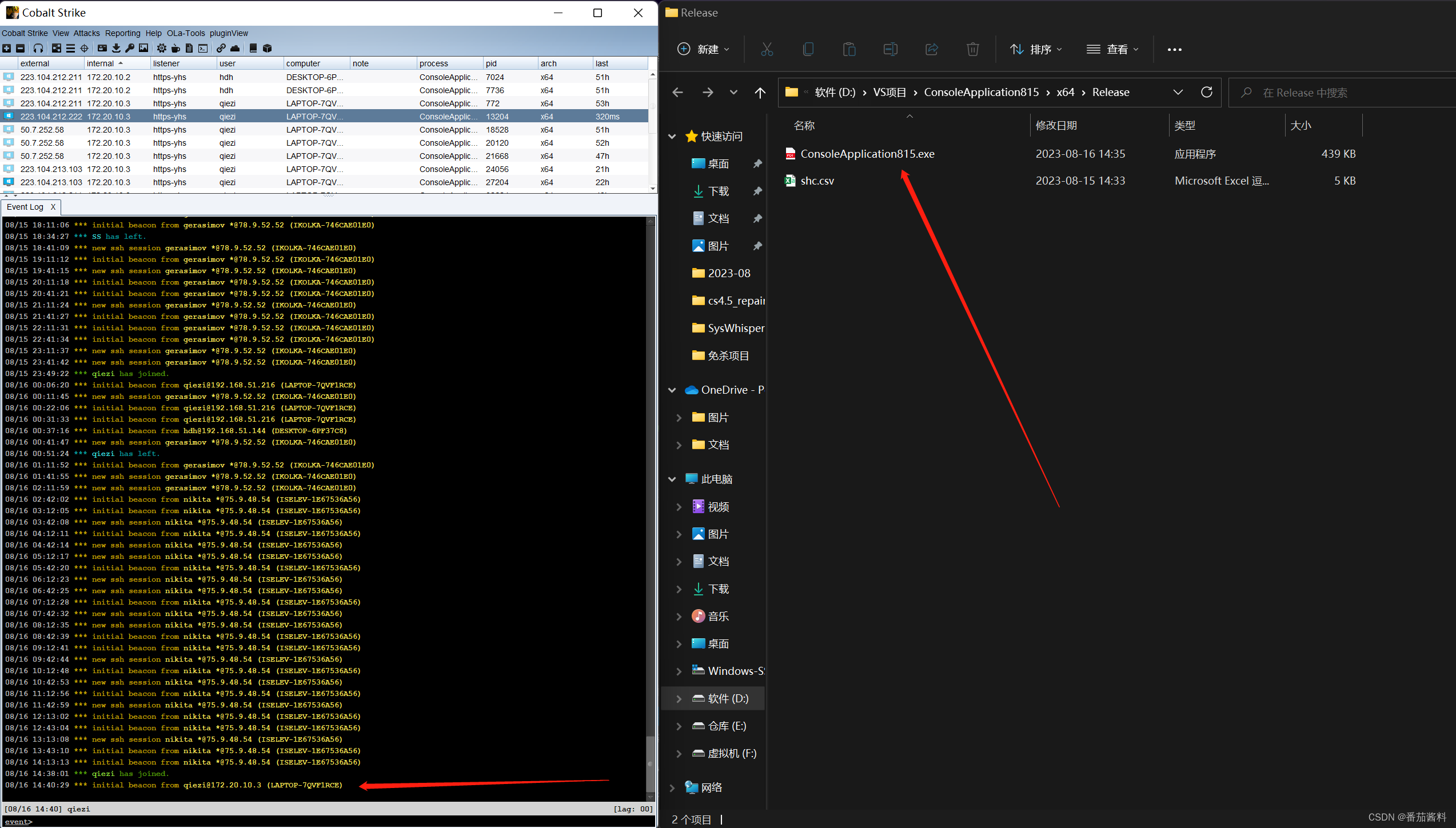
ConsoleApplication815项目(直接加载+VEH Hook Load)
上线图 ConsoleApplication815.cpp #include <iostream> #include<Windows.h> #include "detours.h" #include "detver.h" #pragma comment(lib,"detours.lib")#pragma warning(disable:4996)LPVOID Beacon_address; SIZE_T Beacon…...

事务(SQL)
事务概述 事务是一组操作的集合,他是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向西永提交或撤销操作请求。这组操作,要么全部执行成功,要么全部执行失败。 事务操作 查看/设置事务提交方式 -- 查看/设置事务…...
)
原型,原型链,继承(圣杯模式)
经典模式和圣杯模式区别 经典模式和圣杯模式都是用于解决构造函数继承和原型继承的问题,但它们在实现继承的方式上有所不同。 经典模式是通过将子类的原型对象设置为父类的实例来实现继承,然后将子类的构造函数设置为子类本身。这样子类既可以继承父类…...

远程方法调用中间件Dubbo在spring项目中的使用
Dubbo是一个分布式服务框架,它可以帮助我们快速开发和提供高性能、高可靠性的分布式服务,同时提供服务治理、容错、负载均衡等功能。 使用Dubbo可以分为以下步骤: 引入Dubbo依赖:在项目的pom.xml文件中引入Dubbo的依赖。编写服务…...

MFC -- Date Time Picker 控件使用
当前环境:VS2015 Windows 10 //(一)使用普通函数, 获取当前时间CString strCurrentTime; COleDateTime m_time COleDateTime::GetCurrentTime(); strCurrentTime m_time.Format(_T("%Y-%m-%d %H:%M:%S")); SetDlgIt…...
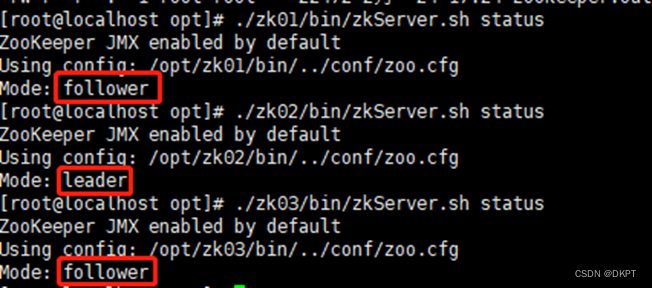
zookeeper 集群
zookeeper 集群 1、zookeeper 集群说明 initLimit 是Zookeeper用它来限定集群中的Zookeeper服务器连接到Leader的时限 syncLimit 限制了follower服务器与leader服务器之间请求和应答之间的时限 服务器名称与地址:集群信息(服务器编号,服务器…...

stable diffusion实践操作-随机种子seed
系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、seed是什么?二、使用步骤1.多批次随机生成多张图片2.提取图片seed3. 根据seed 再次培养4 seed使用4.1 复原别人图4.1 轻微修改4.2 固定某个人物-修改背景 三、差异随机种子1. webUI位置2. 什么…...
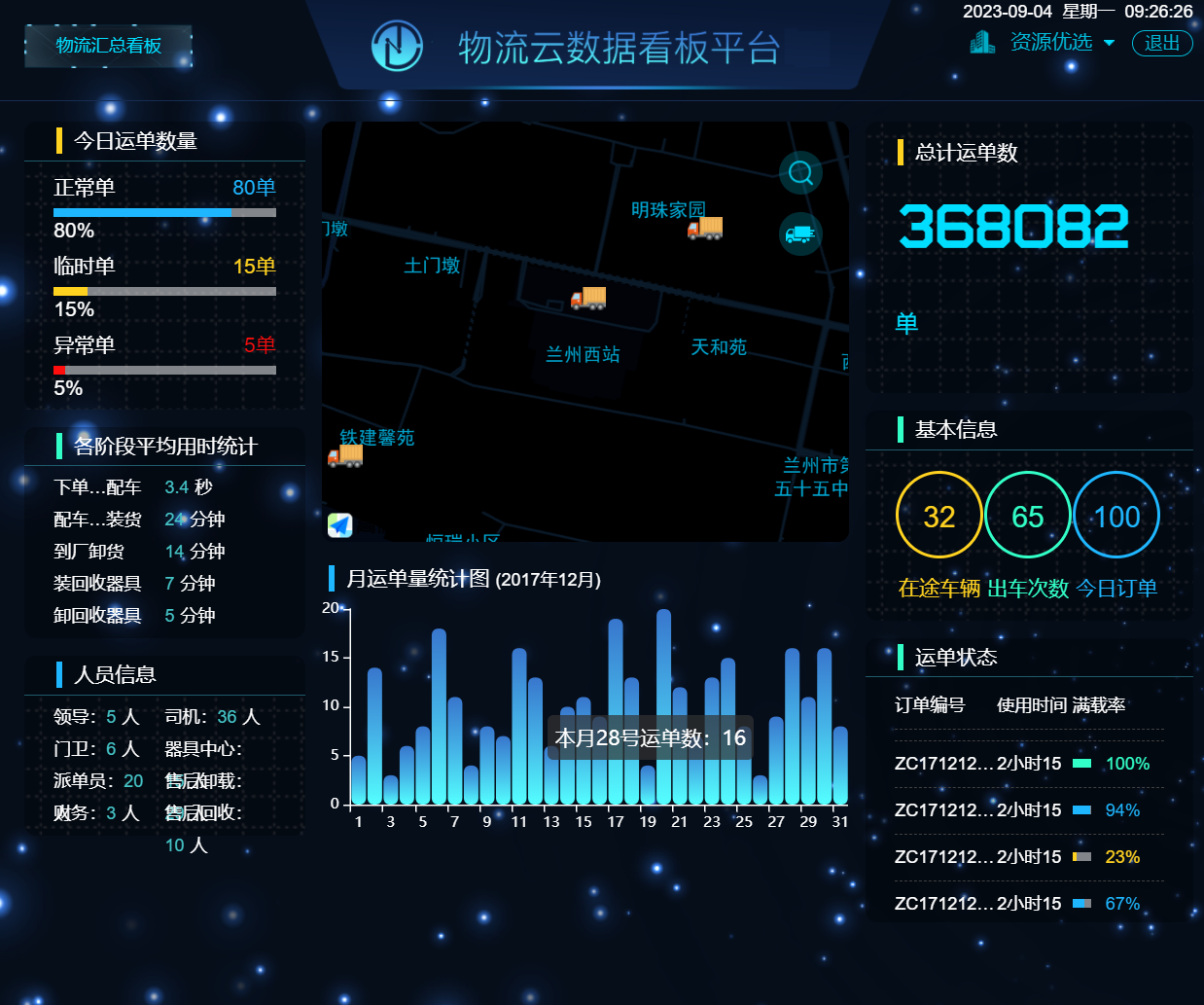
大数据可视化大屏实战项目(4)物流数据云看台(包括动态登陆页面)—HTML+CSS+JS【源码在文末】(可用于比赛项目或者作业参考中)
大数据可视化大屏实战项目(4)物流数据云看台(包括动态登陆页面)—HTMLCSSJS【源码在文末】(可用于比赛项目或者作业参考中🐕🐕🐕) 一,项目概览 ☞☞☞☞☞☞…...

在ubuntu下远程链接仓库gitte/github
后期适当加点图片,提高可读性。 本教程是最基础的连接教程,设计git的操作也仅仅局限于push/pull,如果想全面了解,可以参考廖雪峰git教程 在Ubuntu上初始化本地Git仓库并链接到远程Gitee仓库(github同理),需要按照以下步…...
一些自己整理的工具实用参数
工具实用参数 sqlmap -u: 指定需要测试的目标URL(格式:http://www.example.com/test.php?id1) --cookie: 设置需要发送的 HTTP Cookie,例如:--cookie"sid123456;PHPSESSID654321" --threads:…...

C# Timer定时器
C# Timer定时器 Timer定时器定时器主要用到的就是Timer的Tick事件,另外还要设置时间间隔: 下面这个实力演示了每隔一秒,picturebox中的图片来回切换,每隔一秒,文本框中显示当前时间。 using System; using System.Co…...

oracle怎么删除表索引
Oracle是目前常用的企业级关系型数据库管理系统,用于存储和管理大量数据。在Oracle中,表索引是用于提高查询效率的重要组成部分,但也有时候需要删除表索引。本文将介绍如何在Oracle中删除表索引。 一、查看表索引 在删除表索引之前ÿ…...

【Tkinter系列13/15】标准化外观和选项数据库
27. 标准化外观和选项数据库 可以轻松地将颜色、字体和其他选项应用于 小部件,当您创建它们时。然而 如果您希望很多小部件具有相同的 背景颜色或字体,指定每个都很乏味 每次选项,以及 让用户覆盖您的选择是很好的 他们最喜欢的配色方案、字…...
springboot 集成dubbo
上一篇我们一起认识了Dubbo与RPC,今天我们就来一起学习如何使用Dubbo,并将Dubbo集成到Spring Boot的项目中。我们来看下今天要使用到的软件及版本: 软件 版本 说明 Java 11 Spring Boot 2.7.13 Spring Boot 3.0版本开始,最…...

基于YOLOV8模型和CCPD数据集的车牌目标检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOV8模型和CCPD数据集的车牌目标检测系统可用于日常生活中检测与定位车牌目标,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算…...

net user安全隐患
net user test 123456 /add #添加一个test账户,密码是123456net user test /delete #删除test账户windows administrator权限下删除其他账户,难道不需要知道该账户的密码吗? 以前没太注意,但是这算不算是一个漏洞呢? 另外&#…...

深入剖析Kubernetes之资源模型和GPU 管理
文章目录 资源模型QoS 模型GPU 管理 资源模型 在 Kubernetes 里,Pod 是最小的原子调度单位。这也就意味着,所有跟调度和资源管理相关的属性都应该是属于 Pod 对象的字段。而这其中最重要的部分,就是 Pod 的 CPU 和内存配置,如下所…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
