COMPFEST 15H「组合数学+容斥」
Problem - H - Codeforces
题意:
定义一个集合S为T的孩子是,对于S中的每一个元素x,在T中都能找到x+1。
给定n,k,每一个集合中的元素x必须满足 1 < = x < = k 1<=x<=k 1<=x<=k且 c n t [ x ] < = 1 cnt[x]<=1 cnt[x]<=1,若n个集合重排后对于 1 < i < = n 1<i<=n 1<i<=n都可以满足 S i − 1 S_{i-1} Si−1为 S i S_i Si的孩子,则该n个集合是一个合法序列,求所有合法序列的个数。
思路:
定义 f [ i ] f[i] f[i]为最后一个集合中若 i i i存在,只看 i i i的贡献(可以构成
合法的之前集合的总个数)。
则 f [ 1 ] = 1 , f [ i ] = f [ i − 1 ] + 1 f[1]=1,f[i]=f[i-1]+1 f[1]=1,f[i]=f[i−1]+1,因为最后一个集合里,1只能是自己冒出来的不能是由前面变来的,之后每一个数都可以是自己冒出来的(贡献为1),也可以是将使集合中出现i-1的那个位置上的数提前出现一位,导致原来的i-1变成现在的i。由于最后一个集合中出现每一个数都是独立的,所以可以用乘法原理算得每种情况,求出 p r e [ i ] pre[i] pre[i]表示至少有n-i个空集的集合有多少情况。
AC代码:
#include <bits/stdc++.h>
using namespace std;
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
#define int ll
#define pb push_back
#define eb emplace_back
#define m_p make_pair
const int mod = 998244353;
#define mem(a,b) memset(a,b,sizeof a)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const ll N = 2e5+50;
//__builtin_ctzll(x);后导0的个数
//__builtin_popcount计算二进制中1的个数
int fac[N],inv[N];ll qp(ll a,ll b){ll ans=1;a%=mod;while(b){if(b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans;
}void init(){fac[0]=fac[1]=inv[0]=inv[1]=1;for(int i=2;i<=N;++i){fac[i]=1ll*fac[i-1]*i%mod; //阶乘inv[i]=1ll*inv[mod%i]*(mod-mod/i)%mod; //逆元}for(int i=2;i<=N;++i){inv[i]=1ll*inv[i]*inv[i-1]%mod;}
}void work() {init();int n,k;cin>>n>>k;ll ans=0;for(int i=1;i<=min(n,k);++i){ll res=(fac[i+1]*qp(i+1,k-i)%mod-fac[i]*qp(i,k-i+1)%mod+mod)%mod;//至少有n-(i+1)个空集-至少有n-i个空集ans=(ans+res*fac[n]%mod*inv[n-i]%mod)%mod;//恰有n-i个空集的情况}ans++;cout<<ans<<'\n';
}signed main() {io;int t=1;//cin >> t;while (t--) {work();}return 0;
}
相关文章:

COMPFEST 15H「组合数学+容斥」
Problem - H - Codeforces 题意: 定义一个集合S为T的孩子是,对于S中的每一个元素x,在T中都能找到x1。 给定n,k,每一个集合中的元素x必须满足 1 < x < k 1<x<k 1<x<k且 c n t [ x ] < 1 cnt[x…...
react快速开始(三)-create-react-app脚手架项目启动;使用VScode调试react
文章目录 react快速开始(三)-create-react-app脚手架项目启动;使用VScode调试react一、create-react-app脚手架项目启动1. react-scripts2. 关于better-npm-runbetter-npm-run安装 二、使用VScode调试react1. 浏览器插件React Developer Tools2. 【重点】用 VSCode …...
【C++入门】string类常用方法(万字详解)
目录 1.STL简介1.1什么是STL1.2STL的版本1.3STL的六大组件1.4STL的缺陷 2.string类的使用2.1C语言中的字符串2.2标准库中的string类2.3string类的常用接口说明 (只讲解最常用的接口)2.3.1string类对象的常见构造2.3.2 string类对象的容量操作2.3.3string…...

大数据错误
question1 : Could not locate Hadoop executable: D:\hadoop-3.3.1\bin\winutils.exe - 【已解决】Could not locate executable E:\Hadoop\bin\winutils.exe in the Hadoop binaries._could not locate executable e:\hadoop-3.3.1\bin\wi_君问归期魏有期的博客-CSDN博客 q…...

【Node.js】Express-Generator:快速生成Express应用程序的利器
在Node.js世界中,Express是一个广泛使用的、强大的Web应用程序框架。它为开发者提供了一系列的工具和选项,使得创建高效且可扩展的Web应用程序变得轻而易举。然而,对于初学者来说,配置和初始化Express应用程序可能会有些困难。为了…...

SpringMVC的工作流程及入门
目录 一、概述 ( 1 ) 是什么 ( 2 ) 作用 二、工作流程 ( 1 ) 流程 ( 2 ) 步骤 三、入门实例 ( 1 ) 入门实例 ( 2 ) 静态资源处理 给我们带来的收获 一、概述 ( 1 ) 是什么 SpringMVC是一个基于Java的Web应用开发框架,它是Spring Framework的一部…...
】)
logging.level的含义及设置 【java 日志 (logback、log4j)】
日志级别 trace<debug<info<warn<error<fatal 常用的有:debug,info,warn,error 通常我们想设置日志级别,会用到 logging.level.rootinfo logging.level设置日志级别,后面跟生效的区域。r…...

第 3 章 栈和队列(链栈)
1. 背景说明 链栈是指用单链表实现的栈,其存储结构为链式存储,实现类似于队列的链式实现,不过在插入元素时链栈在头部插入,而 链式队列在尾部插入,本示例中实现为带头结点的链栈,即栈顶元素为栈指针的下一…...

嵌入式面试-经典问题
1、c语言内存模型 2、C语言中的变量定义在什么地方 3、C语言代码如何运行的、关于栈的相关 4、指针函数与函数指针的区分 5、Static关键字的作用 6、const作用 7、进程与线程的区别 8、链表与数组的区别 9、#define宏定义与typedef的区别...
ZLMeidaKit在Windows上启动时:计算机中丢失MSVCR110.dll,以及rtmp推流后无法转换为flv视频流解决
场景 ZLMediaKit在Windows上实现Rtmp流媒体服务器以及模拟rtmp推流和http-flv拉流播放: ZLMediaKit在Windows上实现Rtmp流媒体服务器以及模拟rtmp推流和http-flv拉流播放_zlm流媒体服务器_霸道流氓气质的博客-CSDN博客 按照以上教程启动MediaServer.exe时提示&am…...

项目(智慧教室)第二部分,人机交互页面实现,
使用软件: 1.BmCvtST.exe 这是stm32Cubemx工程下的带三方软件。存在STemWin中。 作用: 图片变成.c文件格式。 2.CodeBlock 3.模拟器工程(具体请看上一节) 一。emWin环境的搭建 1.codeBlock下载 开源免费。 2.使用stm的C…...
【docker】docker的一些常用命令-------从小白到大神之路之学习运维第92天
目录 一、安装docker-ce 1、从阿里云下载docker-cer.epo源 2、下载部分依赖 3、安装docker 二、启用docker 1、启动docker和不启动查看docker version 2、启动服务查看docker version 有什么区别?看到了吗? 3、看看docker启动后的镜像仓库都有什…...
ubuntu18.04.6的安装教程
目录 一、下载并安装virtualbox virtualbox7.0.8版本的安装 二、Ubuntu的下载与安装 ubuntu18.04.6操作系统 下载 安装 一、下载并安装virtualbox VirtualBox是功能强大的x86和AMD64/Intel64虚拟化企业和家庭使用的产品。VirtualBox不仅是面向企业客户的功能极其丰富的高…...
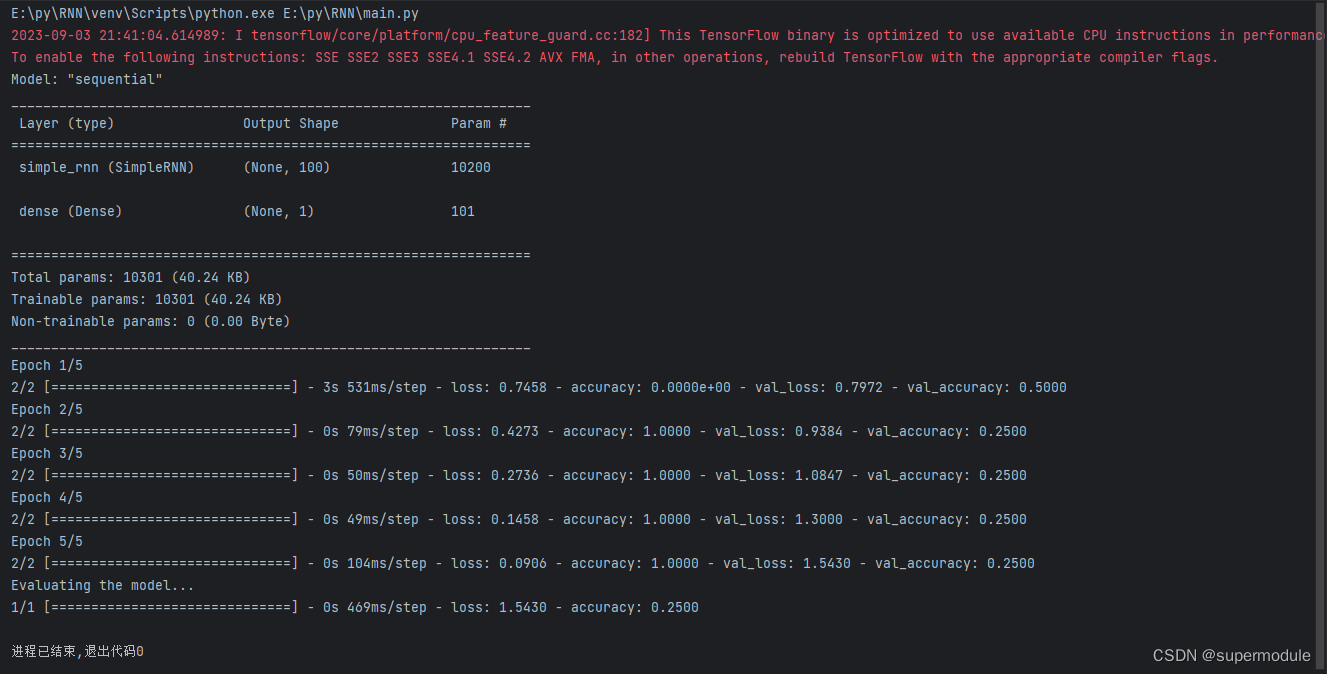
小白的第一个RNN(情感分析模型)
平台:window10,python3.11.4,pycharm 框架:keras 编写日期:20230903 数据集:英语,自编,训练集和测试集分别有4个样本,标签有积极和消极两种 环境搭建 新建文件夹&am…...

华为云 存在部支持迁移的外键解决方法
DRS 检测出源端存在不支持的外键引用操作 MySQL、GaussDB(for MySQL)为源的全量增量或增量迁移、同步场景,以及MySQL、GaussDB(for MySQL)为源灾备场景 表1 源端存在不支持的外键引用操作 预检查项 源端存在不支持的外键引用操作。 描述 同步对象中存在包含CASC…...

C# winform控件和对象双向数据绑定
实现目的: 控件和对象双向数据绑定 实现结果: 1. 对象值 -> 控件值 2. 控件值 -> 对象值 using System; using System.Windows.Forms;namespace ControlDataBind {public partial class MainForm : Form{People people new People();public Mai…...

达梦8 在CentOS 系统下静默安装
确认系统参数 [rootlocalhost ~]# ulimit -a core file size (blocks, -c) unlimited data seg size (kbytes, -d) unlimited【1048576(即 1GB)以上或 unlimited】 scheduling priority (-e) 0 file size (blocks, -f) unlimite…...

flink k8s sink到kafka报错 Failed to get metadata for topics
可能出现的3种报错 -- 报错1 Failed to get metadata for topics [...]. org.apache.kafka.common.errors.TimeoutException: Call-- 报错2 Caused by: org.apache.kafka.common.errors.TimeoutException: Timed out waiting to send the call. Call: fetchMetadata Heartbe…...

利用大模型MoritzLaurer/mDeBERTa-v3-base-xnli-multilingual-nli-2mil7实现零样本分类
概念 1、零样本分类:在没有样本标签的情况下对文本进行分类。 2、nli:(Natural Language Inference),自然语言推理 3、xnli:(Cross-Lingual Natural Language Inference) ,是一种数据集,支持15种语言,数据集包含10个领域,每个领…...

代码随想录二刷day07
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣454. 四数相加 II二、力扣383. 赎金信三、力扣15. 三数之和四、力扣18. 四数之和 前言 提示:这里可以添加本文要记录的大概内容࿱…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
