【力扣】304. 二维区域和检索 - 矩阵不可变 <二维前缀和>
目录
- 【力扣】304. 二维区域和检索 - 矩阵不可变
- 二维前缀和理论
- 初始化
- 计算面积
- 题解
【力扣】304. 二维区域和检索 - 矩阵不可变
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。

提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
- 1 0 5 10^5 105 <= matrix[i][j] <= 1 0 5 10^5 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 1 0 4 10^4 104 次 sumRegion 方法
二维前缀和理论
初始化
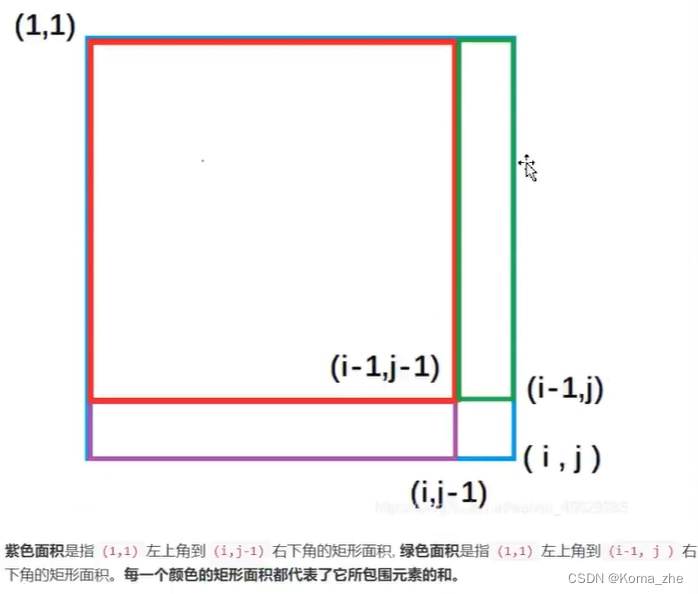
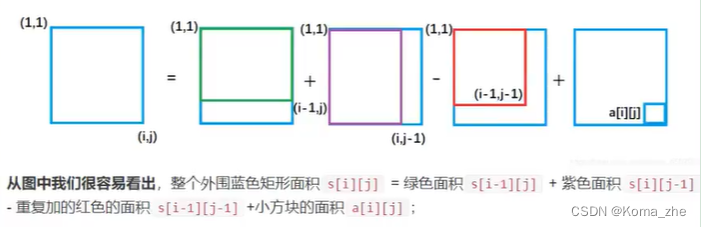
因此二维前缀和预处理公式:
s[i][j] = s[i-1][j] + s[i][j-1] -s[i-1][j-1] + a[i][j]
计算面积
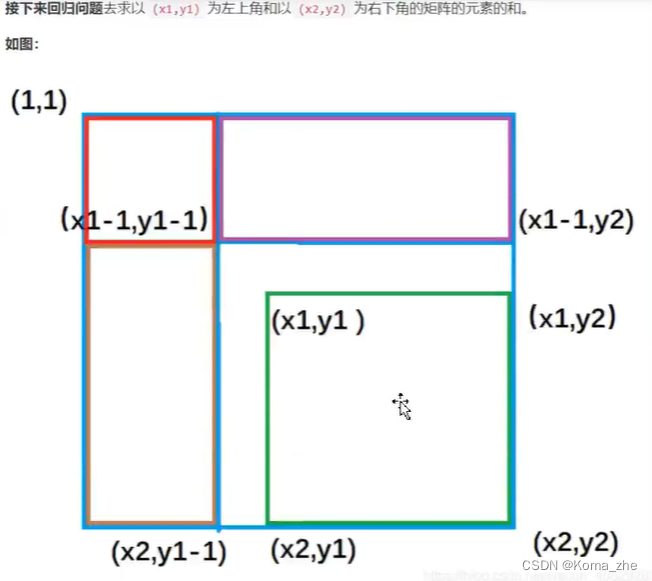
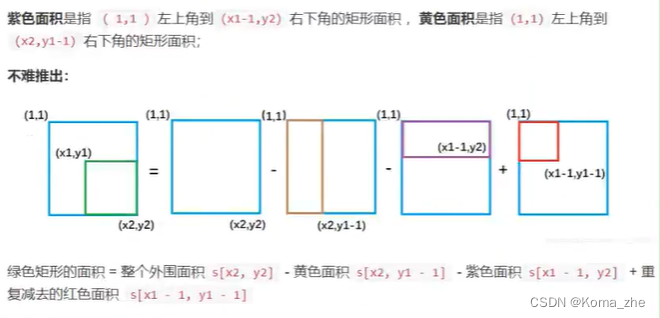
因此二维前缀和计算公式:(以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵的和)
s[x2][y2] - s[x2][y1 - 1] + s[x1 - 1][y2] -s[x1 - 1][y1 - 1]
题解
都加一,数组从(0,0)开始
class NumMatrix {int[][] s;public NumMatrix(int[][] matrix) {int m = matrix.length;if (m > 0) {int n = matrix[0].length;s = new int[m + 1][n + 1];// 初始化for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {s[i + 1][j + 1] = s[i][j + 1] + s[i + 1][j] - s[i][j] + matrix[i][j];}}}}// 计算面积public int sumRegion(int x1, int y1, int x2, int y2) {return s[x2 + 1][y2 + 1] - s[x2 + 1][y1] - s[x1][y2 + 1] + s[x1][y1];}
}
相关文章:

【力扣】304. 二维区域和检索 - 矩阵不可变 <二维前缀和>
目录 【力扣】304. 二维区域和检索 - 矩阵不可变二维前缀和理论初始化计算面积 题解 【力扣】304. 二维区域和检索 - 矩阵不可变 给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, …...
线上问诊:数仓开发(三)
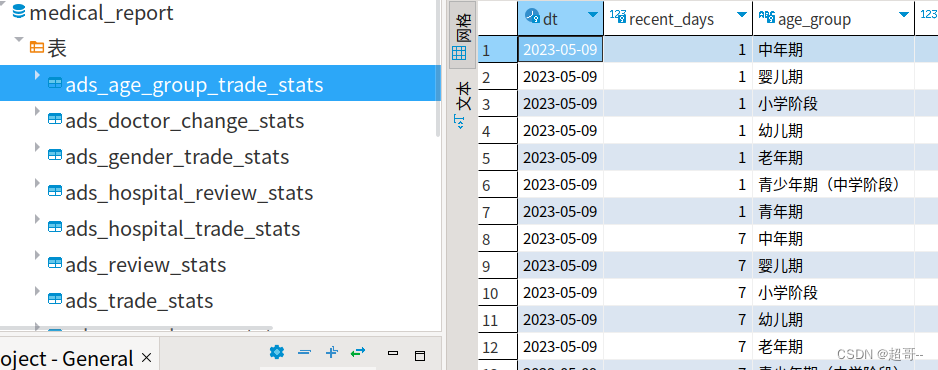
系列文章目录 线上问诊:业务数据采集 线上问诊:数仓数据同步 线上问诊:数仓开发(一) 线上问诊:数仓开发(二) 线上问诊:数仓开发(三) 文章目录 系列文章目录前言一、ADS1.交易主题1.交易综合统计2.各医院交易统计3.各性…...
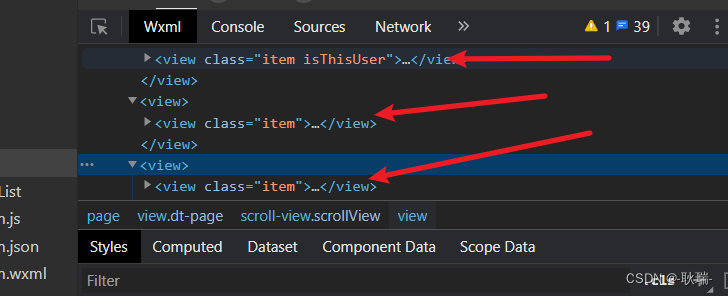
微信小程序 通过响应式数据控制元素class属性
我想大家照这个和我最初的目的一样 希望有和vue中v-bind:class一样方便的指令 但答案不太尽人意 这里 我们只能采用 三元运算符的形式 参考代码如下 <view class"item {{ userId item.userId ? isThisUser : }}"> </view>这里 我们判断 如果当前ite…...

linux并发服务器 —— linux网络编程(七)
网络结构模式 C/S结构 - 客户机/服务器;采用两层结构,服务器负责数据的管理,客户机负责完成与用户的交互;C/S结构中,服务器 - 后台服务,客户机 - 前台功能; 优点 1. 充分发挥客户端PC处理能力…...

Java后端开发面试题——企业场景篇
单点登录这块怎么实现的 单点登录的英文名叫做:Single Sign On(简称SSO),只需要登录一次,就可以访问所有信任的应用系统 JWT解决单点登录 用户访问其他系统,会在网关判断token是否有效 如果token无效则会返回401&am…...
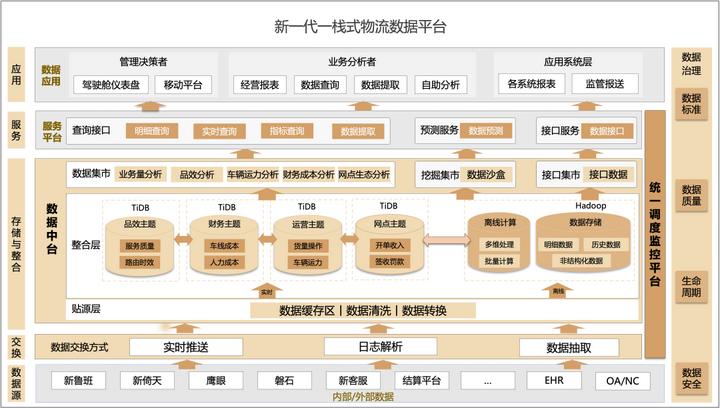
TiDB x 安能物流丨打造一栈式物流数据平台
作者:李家林 安能物流数据库团队负责人 本文以安能物流作为案例,探讨了在数字化转型中,企业如何利用 TiDB 分布式数据库来应对复杂的业务需求和挑战。 安能物流作为中国领先的综合型物流集团,需要应对大规模的业务流程ÿ…...

负载均衡算法实现
负载均衡算法实现 负载均衡介绍 负责均衡主要有以下五种方法实现: 1、轮询法 将请求按顺序轮流地分配到后端服务器上,它均衡地对待后端的每一台服务器,而不关心服务器实际的连接数和当前的系统负载; 2、随机法 通过系统的随机算法&#…...

Flutter 完美的验证码输入框 转载
刚开始看到这个功能的时候一定觉得so easy,开始的时候我也是这么觉得的,这还不简单,然而真正写的时候才发现并没有想象的那么简单。 先上图,不上图你们都不想看,我难啊,到Github: https://gith…...
)
SpringBoot整合Jpa实现增删改查功能(提供Gitee源码)
前言:在日常开发中,总是撰写一些简单的SQL会非常耗时间,Jpa可以完美的帮我们提高开发的效率,对于常规的SQL不需要我们自己撰写,相对于MyBatis有着更简单易用的功能,但是MyBatis自由度相对于Jpa会更高一些&a…...

微服务[Nacos]
CAP 1)一致性(Consistency) (所有节点在同一时间具有相同的数据) 2)可用性(Availability)(保证每个请求不管成功或者失败都有响应) 3)分区容错(Partition tolerance)(系统中任意信息的丢失或失败不会影响系统的继续运作) 一、虚拟机镜像准备 …...

8K视频来了,8K 视频编辑的最低系统要求
当今 RED、Canon、Ikegami、Sony 等公司的 8K 摄像机以及 8K 电视,许多视频内容制作人和电影制作人正在认真考虑 8K 拍摄、编辑和后期处理,需要什么样的系统来处理如此海量的数据? 中央处理器(CPU) 首先,…...

AsyncContext优雅实现HTTP长轮询接口
一、背景 接到一个需求,实现方案时需要提供一个HTTP接口,接口需要hold住5-8秒,轮询查询数据库,一旦数据库中值有变化,取出变化的值进行处理,处理完成后返回响应。这不就是长轮询吗,如何优雅的实…...
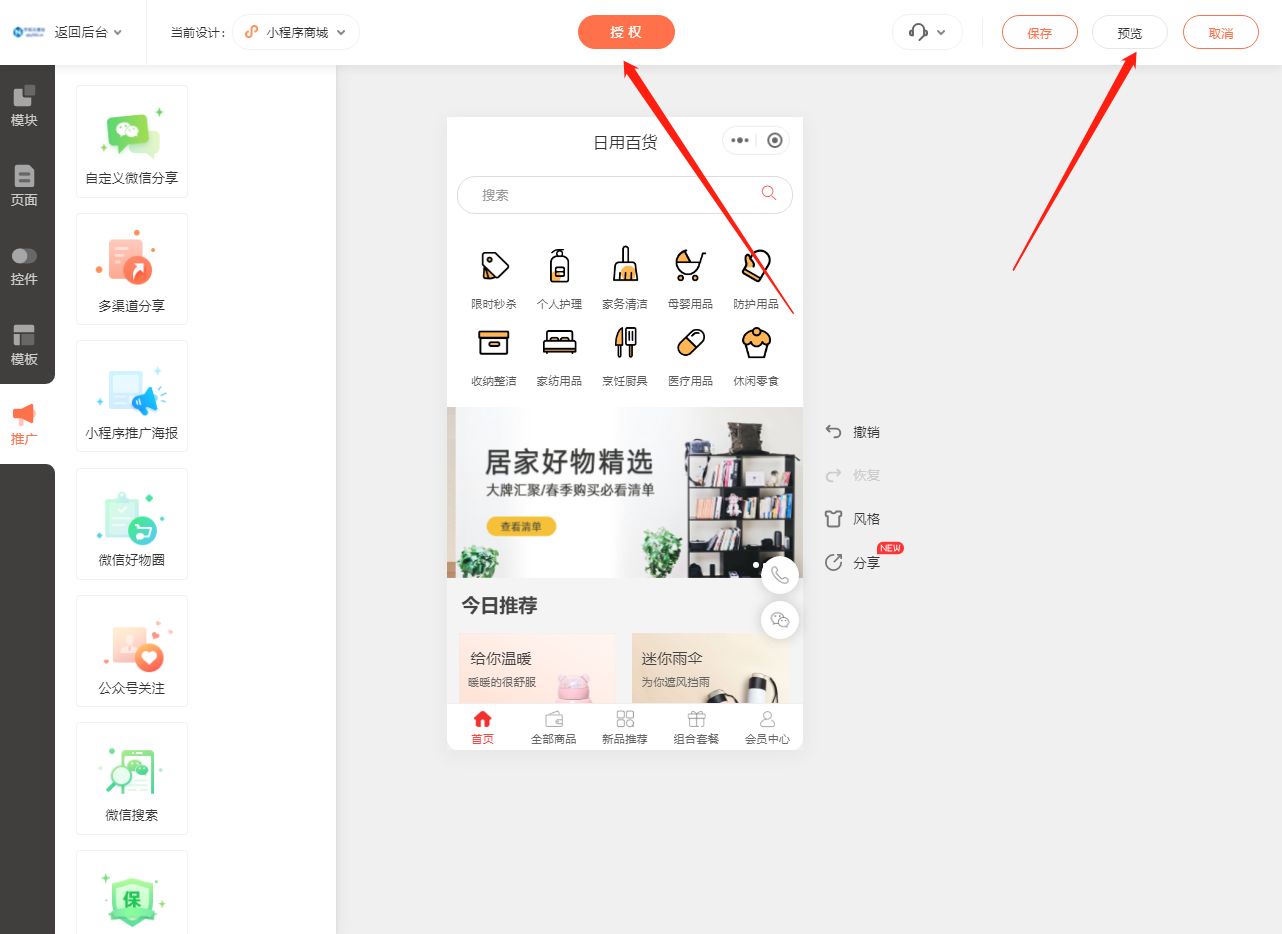
如何制作一个百货小程序
在这个数字化时代,小程序已成为各行各业的必备工具。其中,百货小程序因其便捷性和多功能性,越来越受到人们的青睐。那么,如何制作一个百货小程序呢?下面,我们就详细介绍一下无需编写代码的步骤。 一、进入后…...
【人工智能】—局部搜索算法、爬山法、模拟退火、局部剪枝、遗传算法
文章目录 局部搜索算法内存限制局部搜索算法示例:n-皇后爬山算法随机重启爬山模拟退火算法局部剪枝搜索遗传算法小结 局部搜索算法 在某些规模太大的问题状态空间内,A*往往不够用 问题空间太大了无法访问 f 小于最优的所有状态通常,甚至无法储…...
MATLAB旋转动图的绘制
MATLAB旋转动图的绘制 文章目录 MATLAB旋转动图的绘制1、动图效果2、matlab代码 利用matlab实现三维旋转动图的绘制。 1、动图效果 2、matlab代码 close all clear clcf(x,y,z)(x.^2 (9./4).*y.^2 z.^2 - 1).^3 - x.^2.*z.^3 - (9./80).*y.^2.*z.^3; [x,y,z]meshgrid(linspac…...
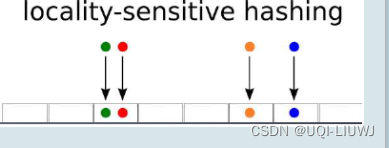
算法笔记 近似最近邻查找(Approximate Nearest Neighbor Search,ANN)
1 介绍 精准最近邻搜索中数据维度一般较低,所以会采用穷举搜索,即在数据库中依次计算其中样本与所查询数据之间的距离,抽取出所计算出来的距离最小的样本即为所要查找的最近邻。 当数据量非常大的时候,搜索效率急剧下降。——>…...
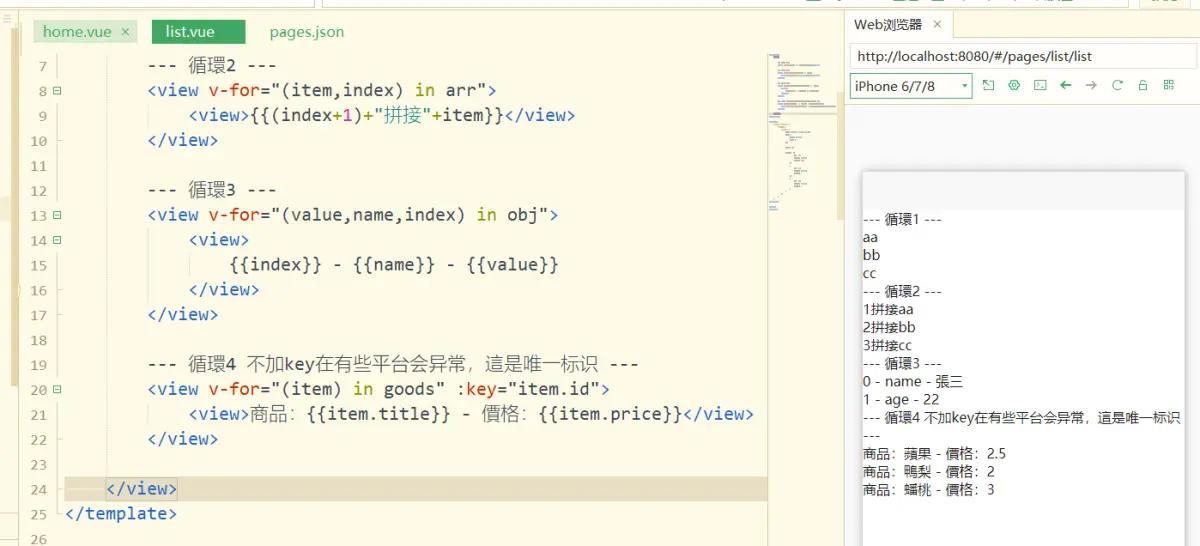
uni-app 之 vue语法
uni-app 之 vue语法 image.png --- v-html 字符 --- image.png <template><view><view>{{title}}</view>--- v-html 字符 ---<view>{{title2}}</view><view v-html"title2"></view><view>{{arr}}</view&g…...
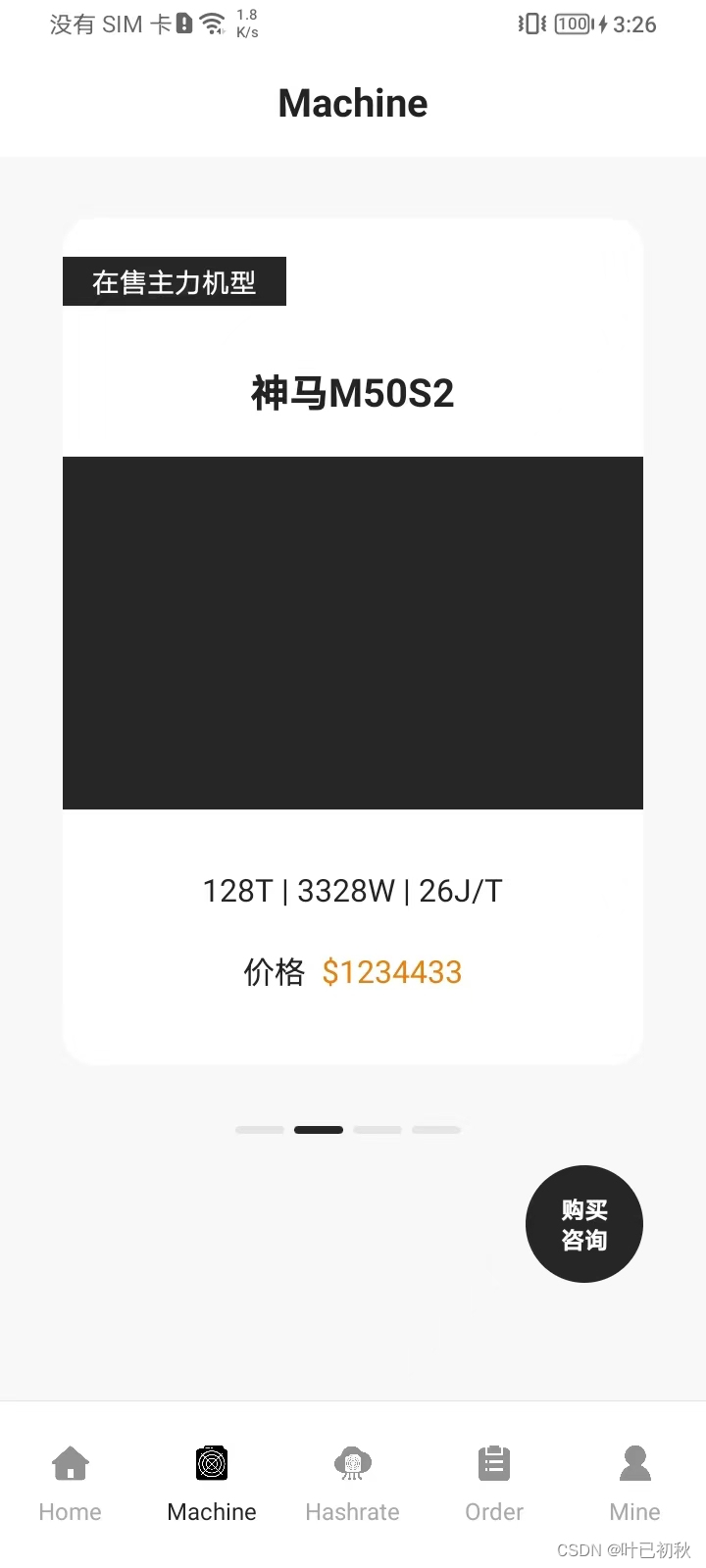
Android之RecyclerView仿ViewPage滑动
文章目录 前言一、效果图二、实现步骤1.xml主布局2.所有用到的drawable资源文件3.xml item布局4.adapter适配器5.javabean实体类6.activity使用 总结 前言 我们都知道ViewPageFragment滑动,但是的需求里面已经有了这玩意,但是在Fragment中还要有类似功能…...

【owt-server】AudioSendAdapter分析
owt-server/source/core/rtc_adapter/AudioSendAdapter.cc使用其他线程运行rtprtcpmodule taskrunner分配线程:因此,对rtprtcp的使用都是加了mutex的:首先为音频发送者生成一个随机的ssrc并注册 // SSRCs of this type.std::vector<uint32_t> ssrcs_;发送还要向rtprtc…...

day33 List接口
List实现类 java.util.ArrayList: 底层通过数组保存数据 , 查询快,增删慢 java.util.LinkedList: 底层通过链表保存数据, 查询慢,增删快 如果对操作性能没有特殊要求,我们一般选择ArrayList…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
