【人工智能】—局部搜索算法、爬山法、模拟退火、局部剪枝、遗传算法
文章目录
- 局部搜索算法
- 内存限制
- 局部搜索算法
- 示例:n-皇后
- 爬山算法
- 随机重启爬山
- 模拟退火算法
- 局部剪枝搜索
- 遗传算法
- 小结
局部搜索算法
-
在某些规模太大的问题状态空间内,A*往往不够用

- 问题空间太大了
- 无法访问 f 小于最优的所有状态
- 通常,甚至无法储存整个边缘队列
-
解决方案
- 设计选择更好的启发式函数
- Greedy hill-climbing (fringe size = 1)
- Beam search (limited fringe size)
内存限制
- 瓶颈:内存不足,无法存储整个边缘队列
- 爬山搜索:
- 只有“最佳”节点保留在周围,没有边缘队列
- 通常按h优先选择继任者(贪婪的爬山)
- 与贪婪的回溯相比,它仍然有边缘队列
- 剪枝搜索(有限内存搜索)
- 介于两者之间:保持边缘中的K个节点
- 根据需要转储优先级最低的节点
- 可以单独按h(贪婪剪枝搜索)或h+g(有限内存A*)进行优先级排序
局部搜索算法
- 在许多优化问题中,通往目标的路径是不相关的;目标状态本身就是解决方案
- 状态空间=“完整”配置集(完全状态)
- 查找满足约束的配置,例如n皇后
- 在这种情况下,我们可以使用本地搜索算法
- 保持一个单一的“当前”状态,尝试改善它
- 直到你无法让它变得更好
- 恒定空间,适合在线和离线搜索
- 通常效率更高(但不完备)
示例:n-皇后
- 将n个皇后区放在n×n板上,同一行、同一列或同一对角线上没有两个皇后区#

爬山算法
- 简单、概括的想法:
- 从任何地方开始
- 总是选择最好的邻居
- 如果没有邻居的分数比当前分数高,退出
- 这在理论上效果很糟糕,因为他不具有完备性(算法不会陷入死循环,即一定能结束)也不保证得到最优解
- 问题:根据初始状态,可能会陷入局部最大值

- 随机重新开始爬山算法一定程度克服了局部最大值
- 随机侧向移动逃离肩膀
- 但可能在最大值处循环
随机重启爬山
-
非常简单的修改:
- 当被卡住时,随机选择一个新的启动状态,然后从那里重新运行爬山
- 重复此操作k次
- 返回k个局部最优值中的最佳值
-
可以做到非常高效
-
每当使用爬山时都应该尝试
-
快速、易于实施;对于解决方案空间表面不太“颠簸”(即不太多局部最大值)的许多应用来说,效果很好
-
仍然以8皇后问题为例:

- h=直接或间接相互攻击的成对皇后数量
- 对于上述状态,h=17
- 一个局部最优解如下:h=1

模拟退火算法
-
思想: 通过允许一些“坏”动作,但逐渐降低其频率,来逃避局部最大值

-
可以证明:如果T下降得足够慢,那么模拟退火搜索将找到概率接近1的全局最优
-
广泛应用于超大规模集成电路布局、航空公司调度等
局部剪枝搜索
- 跟踪k个状态,而不仅仅是一个。
- 从k个随机生成的状态开始。
- 在每次迭代时,生成所有k个状态的所有后续状态。
- 如果任何一个是目标状态,则停止;否则,从完整列表中选择k个最佳继任者,然后重复。
- 像贪婪搜索一样,但始终保持K状态:

- 多种实用设置中的最佳选择
- 与并行运行的k个搜索不同!
- 找到好状态的搜索,会招募其他搜索加入他们
- 变量:分支大小,鼓励多样性?
- 问题:通常情况下,所有k个状态最终都在同一个局部山丘上
- 思想:随机选择k个继任者,偏向于优秀的继任者
遗传算法
- 遗传算法使用自然选择隐喻
- 通过组合两个父状态生成后续状态
- 从k个随机生成的状态开始(总体种群)
- 状态表示为有限字母表上的字符串(通常是0和1的字符串)
- 评价函数(适应度函数适应度函数). 值越高,状态越好。
- 通过选择、交叉和突变产生下一代状态(选择,杂交,变异)
- 示例:每个状态由8个数字表示,按照概率随机选择两对交叉,适应度就是互不攻击的皇后对数,概率就是适应度的占比


小结
- 局部搜索算法——通往目标的路径是不相关的;目标状态本身就是解决方案,保持单一的“当前”状态,并尝试改进它
- 登山搜索
- 根据初始状态,可能会陷入局部最大值
- 模拟退火搜索
- 通过允许一些“坏”的移动来逃避局部最大值,但逐渐降低其频率
- 局部剪枝搜索
- 跟踪k个状态,而不仅仅是一个
- 好的启发式搜索能大大提高搜索性能
- 但由于启发式搜索需要抽取与问题本身有关的特征信息,而这种特征信息的抽取有时会比较困难,因此盲目搜索仍不失为一种有用的搜索策略
- 好的搜索策略应该
- 引起运动—避免原地踏步
- 系统—避免兜圈
- 运用启发函数—缓解组合爆炸
- 搜索树 vs 搜索图
- 搜索树:结点有重复,但登记过程简单
- 搜索图:结点无重复,但登记过程复杂(每次都要查重)
- 省空间,费时间。
相关文章:

【人工智能】—局部搜索算法、爬山法、模拟退火、局部剪枝、遗传算法
文章目录 局部搜索算法内存限制局部搜索算法示例:n-皇后爬山算法随机重启爬山模拟退火算法局部剪枝搜索遗传算法小结 局部搜索算法 在某些规模太大的问题状态空间内,A*往往不够用 问题空间太大了无法访问 f 小于最优的所有状态通常,甚至无法储…...
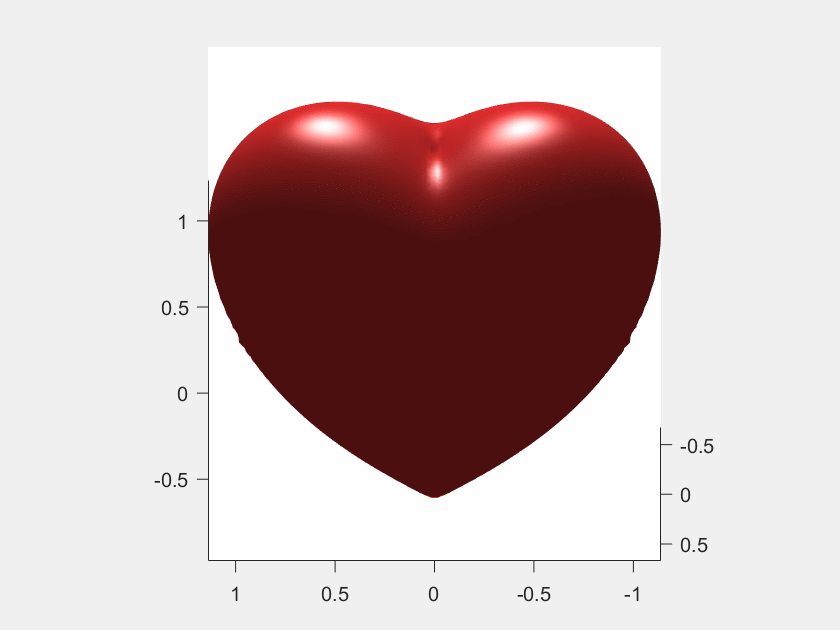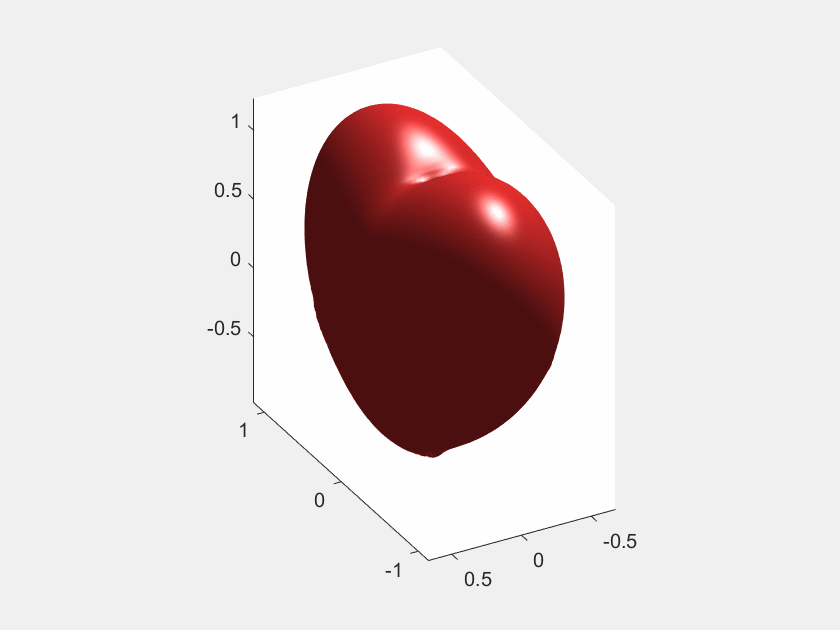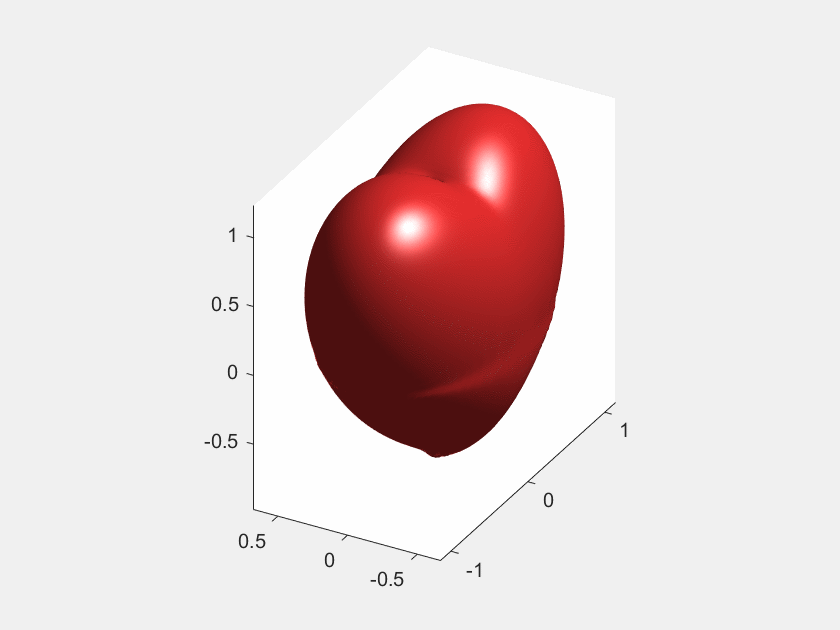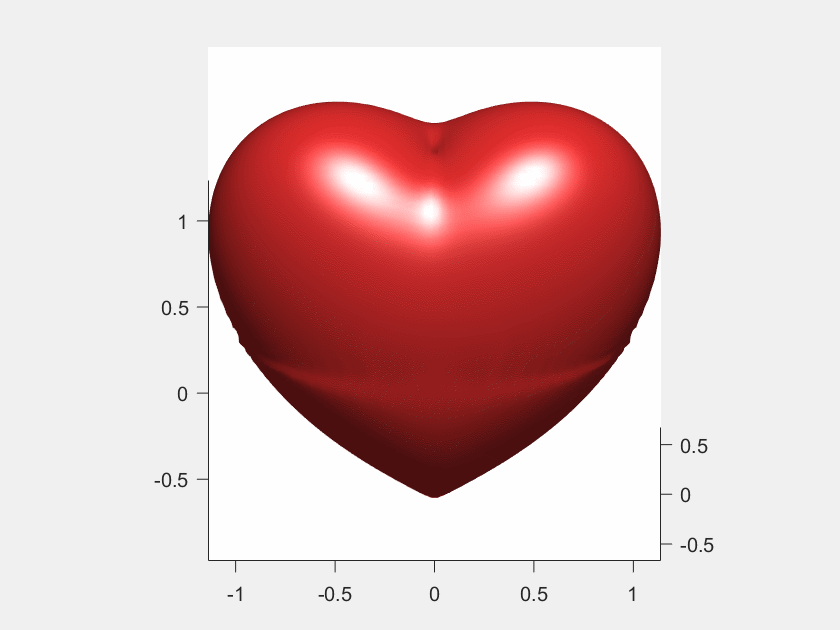
MATLAB旋转动图的绘制
MATLAB旋转动图的绘制 文章目录 MATLAB旋转动图的绘制1、动图效果2、matlab代码 利用matlab实现三维旋转动图的绘制。 1、动图效果 2、matlab代码 close all clear clcf(x,y,z)(x.^2 (9./4).*y.^2 z.^2 - 1).^3 - x.^2.*z.^3 - (9./80).*y.^2.*z.^3; [x,y,z]meshgrid(linspac…...
算法笔记 近似最近邻查找(Approximate Nearest Neighbor Search,ANN)
1 介绍 精准最近邻搜索中数据维度一般较低,所以会采用穷举搜索,即在数据库中依次计算其中样本与所查询数据之间的距离,抽取出所计算出来的距离最小的样本即为所要查找的最近邻。 当数据量非常大的时候,搜索效率急剧下降。——>…...
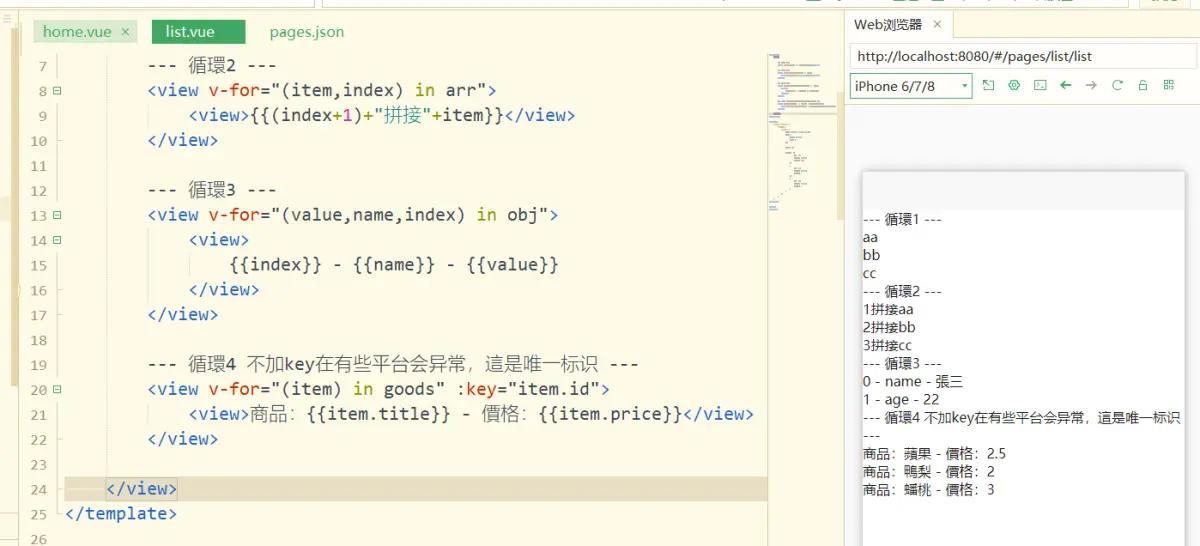
uni-app 之 vue语法
uni-app 之 vue语法 image.png --- v-html 字符 --- image.png <template><view><view>{{title}}</view>--- v-html 字符 ---<view>{{title2}}</view><view v-html"title2"></view><view>{{arr}}</view&g…...
Android之RecyclerView仿ViewPage滑动
文章目录 前言一、效果图二、实现步骤1.xml主布局2.所有用到的drawable资源文件3.xml item布局4.adapter适配器5.javabean实体类6.activity使用 总结 前言 我们都知道ViewPageFragment滑动,但是的需求里面已经有了这玩意,但是在Fragment中还要有类似功能…...

【owt-server】AudioSendAdapter分析
owt-server/source/core/rtc_adapter/AudioSendAdapter.cc使用其他线程运行rtprtcpmodule taskrunner分配线程:因此,对rtprtcp的使用都是加了mutex的:首先为音频发送者生成一个随机的ssrc并注册 // SSRCs of this type.std::vector<uint32_t> ssrcs_;发送还要向rtprtc…...

day33 List接口
List实现类 java.util.ArrayList: 底层通过数组保存数据 , 查询快,增删慢 java.util.LinkedList: 底层通过链表保存数据, 查询慢,增删快 如果对操作性能没有特殊要求,我们一般选择ArrayList…...

云原生周刊:Linkerd 发布 v2.14 | 2023.9.4
开源项目推荐 Layerform Layerform 是一个 Terraform 包装器,可帮助工程师使用纯 Terraform 文件构建可重用的基础设施。 为了实现重用,Layerform 引入了层的概念。每层都包含一些基础设施,并且可以堆叠在另一层之上。 除了更易于使用之外…...
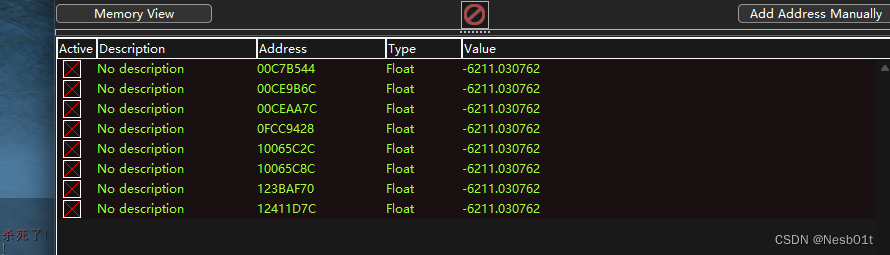
CS420 课程笔记 P5 - 内存编辑 数据类型
文章目录 IntroductionData typesBooleansNegative numbers (Signed integers)Floating-point numbers (fractional numbers) Unknown value scansHealth findingFloat finding (Player position hack / Teleport hack) Additional things Introduction 这节课将结束数据类型并…...

oracle报错 ORA-02290: 违反检查约束条件问题
保存数据库信息时,提示违反检查约束条件,如图: org.springframework.dao.DataIntegrityViolationException: ### Error updating database. Cause: java.sql.SQLIntegrityConstraintViolationException: ORA-02290: 违反检查约束条件 (MXUSER…...
Prometheus + grafana 的监控平台部署
一、Prometheus安装 tar -zxvf prometheus-2.44.0.linux-amd64.tar.gz -C /opt/module/ sudo chown -R bigdata:bigdata /opt/module/prometheus-2.44.0.linux-amd64 mv /opt/module/prometheus-2.44.0.linux-amd64 /opt/module/prometheus-2.44.0 ln -s /opt/module/promethe…...

npm、yarn、pnpm
一、简介 CommonJS 的出现,使 node 环境下的 JS 代码可以用模块更加细粒度的划分。一个类、一个函数、一个对象、一个配置等等均可以作为模块,这种细粒度的划分,是开发大型应用的基石。 为了解决在开发过程中遇到的常见问题,比如…...
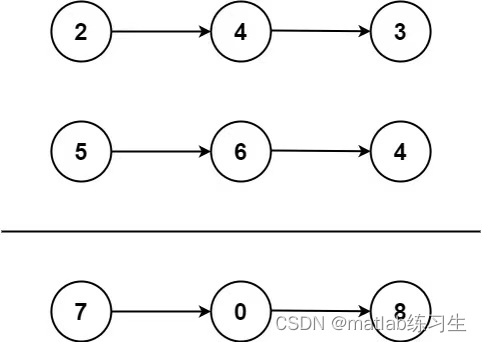
力扣|两数相加
先放题目: 给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请你将两个数相加,并以相同形式返回一个表示和的链表。 你可以假设除了数字 0 之外,…...
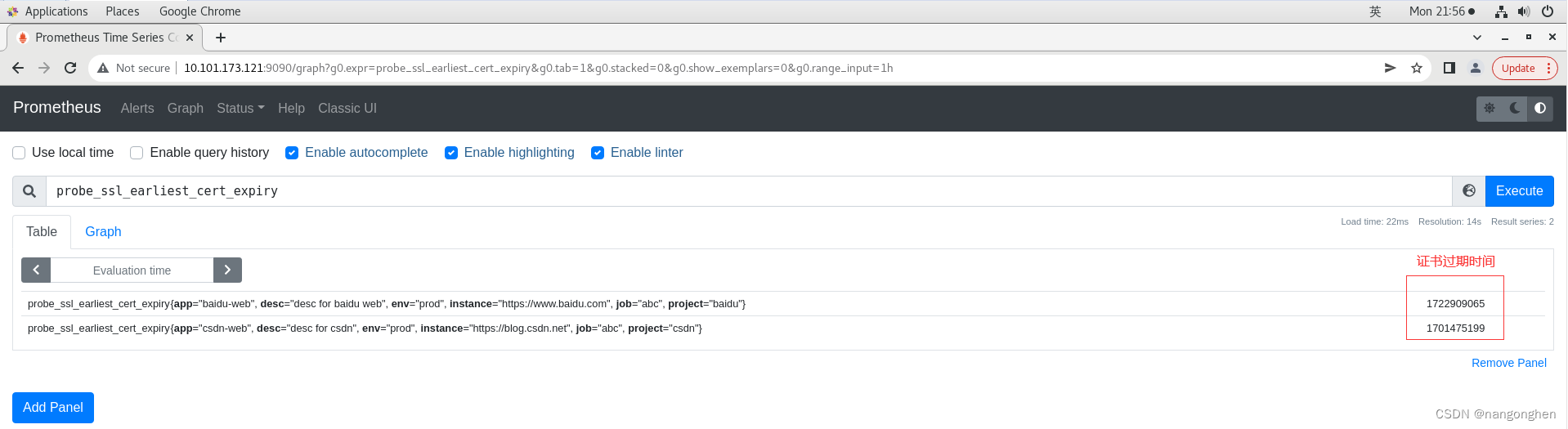
prometheus通过blackbox-exporter监控web站点证书
1 概述 线上站点普遍是https,因此监控https web站点的证书的过期时间,是一个基础性需求。例如,证书过期会导致tls握手失败,进而导致用户无法正常访问web站点。 blackbox-expoter是一个web服务,它暴露了一个接口&#…...
CentOS7 Hadoop3.3.0 安装与配置
一、安装JDK 1、创建文件夹tools和training用于存放压缩包和解压使用,tools存放压缩包,training用于解压后安装jdk和hadoop的路径。 1)回到路径为 / 的位置 cd /2) 创建 tools 和 training mkdir toolsmkdir training3) 进入tools文件夹 …...

2023年9月CDGA/CDGP数据治理认证考试报名,当然弘博创新
据DAMA中国官方网站消息,2023年度第三期DAMA中国CDGA和CDGP认证考试定于2023年9月23日举行。 报名通道现已开启,相关事宜通知如下: 考试科目: 数据治理工程师(CertifiedDataGovernanceAssociate,CDGA) 数据治理专家(CertifiedDataGovernanc…...
Re45:读论文 GPT-1 Improving Language Understanding by Generative Pre-Training
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文全名:Improving Language Understanding by Generative Pre-Training 论文下载地址:https://www.mikecaptain.com/resources/pdf/GPT-1.pdf 本文是2018年OpenAI的工作,…...

VB.NET 如何将某个Excel的工作表中复制到另一个的Excel中的工作表中https://bbs.csdn.net/topics/392861034
参考http://share.freesion.com/306372/可以实现直接拷贝指定表 Private Sub Excel复制工作簿()Dim myExcelApp As New Microsoft.Office.Interop.Excel.ApplicationmyExcelApp.Workbooks.Open(System.Environment.CurrentDirectory "\\测试用例.xlsx", Type.Missin…...

深入解析Kotlin类与对象:构造、伴生、单例全面剖析
前言 本篇文章将带您了解Kotlin编程中的重要概念:类及构造函数、访问修饰符、伴生对象和单例模式。就像搭积木一样,我们会逐步揭开这些概念的面纱,让您轻松理解它们的作用和用法。无论您是编程新手还是有经验的开发者,本文都将为…...
JavaScript构造函数
1、构造函数: 是一个函数,是通过new运算符进行调用,生成一个特殊的对象并返回。 function 函数名([参数]){ this.属性名 ‘属性值’ ... this.属性名 function([参数]){ 函数体语句 } } 通常情况下,建议构造函数的首字母大写 …...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
