代码随想录算法训练营第42天 | ● 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集
文章目录
- 前言
- 一、01背包问题,你该了解这些!
- 二、01背包问题,你该了解这些! 滚动数组
- 三、416. 分割等和子集
- 总结
前言
01背包
一、01背包问题,你该了解这些!
- 确定dp数组以及下标的含义
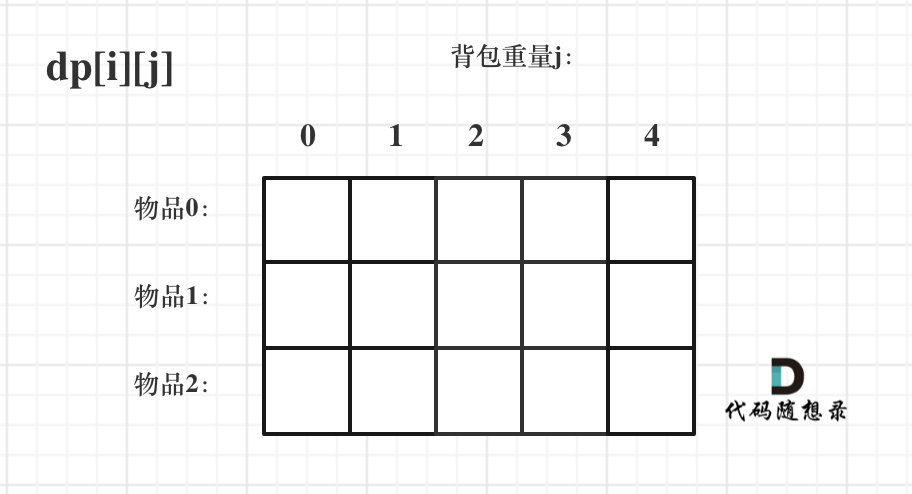
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
只看这个二维数组的定义,大家一定会有点懵,看下面这个图:
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
- 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
初始-1,初始-2,初始100,都可以!
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
先遍历 物品还是先遍历背包重量呢? 答案是都可以(仅针对二维数组)
为什么也是可以的呢?
要理解递归的本质和递推的方向。
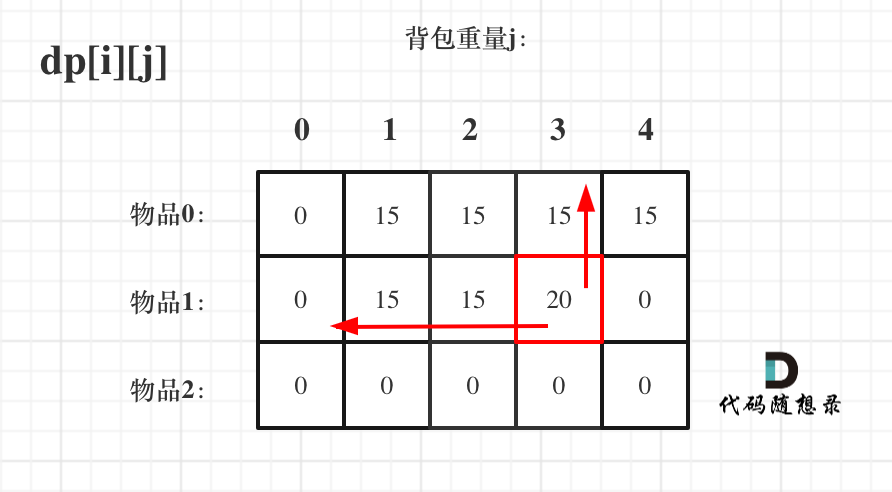
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
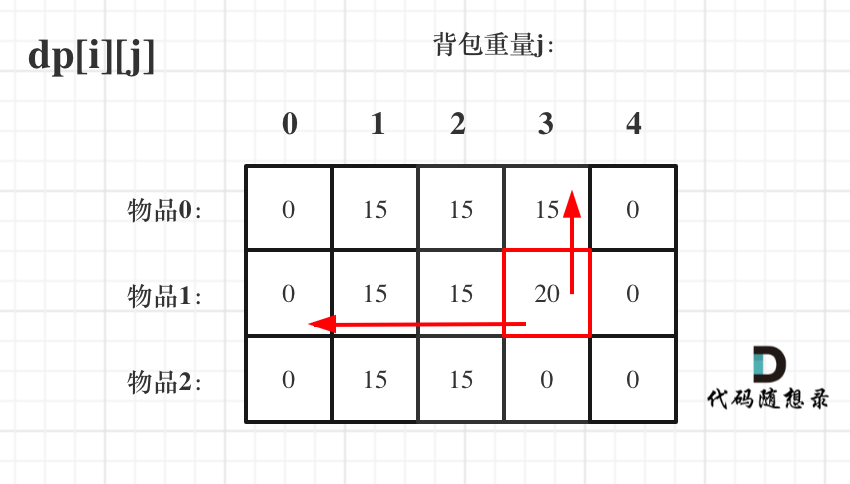
再来看看先遍历背包,再遍历物品呢,如图:
大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!
举例推导dp数组
二、01背包问题,你该了解这些! 滚动数组
- 确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
- 一维dp数组的递推公式
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
- 一维dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
- 一维dp数组遍历顺序
这里大家发现和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
那么问题又来了,为什么二维dp数组历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
(如何这里读不懂,大家就要动手试一试了,空想还是不靠谱的,实践出真知!)
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
(这里如果读不懂,就再回想一下dp[j]的定义,或者就把两个for循环顺序颠倒一下试试!)
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!,这一点大家一定要注意。
举例推导dp数组
三、416. 分割等和子集
背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
动规五部曲分析如下:
- 确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
有录友可能想,那还有装不满的时候?
拿输入数组 [1, 5, 11, 5],举例, dp[7] 只能等于 6,因为 只能放进 1 和 5。
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
- 确定递推公式 01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- dp数组如何初始化
在01背包,一维dp如何初始化,已经讲过,
从dp[j]的定义来看,首先dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
- 确定遍历顺序 举例推导dp数组 如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
class Solution {public boolean canPartition(int[] nums) {if(nums == null || nums.length == 0) return false;int n = nums.length;int sum = 0;for(int num:nums){sum += num;}if(sum % 2 != 0) return false;int target = sum/2;int[] dp = new int[target+1];for(int i = 0;i<n;i++){for(int j =target;j>=nums[i];j--){dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);}//剪枝一下,每一次完成內層的for-loop,立即檢查是否dp[target] == target,優化時間複雜度(26ms -> 20ms)if(dp[target] == target) return true;}return dp[target] == target;}
}总结
背包
相关文章:
代码随想录算法训练营第42天 | ● 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集
文章目录 前言一、01背包问题,你该了解这些!二、01背包问题,你该了解这些! 滚动数组三、416. 分割等和子集总结 前言 01背包 一、01背包问题,你该了解这些! 确定dp数组以及下标的含义 对于背包问题&#x…...
解决DNS服务器未响应错误的方法
当你将设备连接到家庭网络或具有互联网接入功能的Wi-Fi热点时,由于各种原因,互联网连接可能无法正常工作。本文中的说明适用于Windows 10、Windows 8和Windows 7。 无法连接到DNS服务器的原因 故障的一类与域名系统有关,域名系统是世界各地互联网提供商使用的分布式名称…...
SpringBoot的HandlerInterceptor拦截器使用方法
一、创建拦截器 通过实现HandlerInterceptor接口创建自己要使用的拦截器 import org.springframework.context.annotation.Configuration; import org.springframework.web.servlet.HandlerInterceptor; import org.springframework.web.servlet.ModelAndView; import javax.…...

java 常用 jar 包
1 Lombok 是一个 java 类库,它利用注解方式自动生成 java bean 中 getter、setter、equals 等方法,还能自动生成 logger、toString、hashCode、builder 等 日志相关变量、Object 类方法或设计模式相关的方法,能够让你的 代码更简洁࿰…...
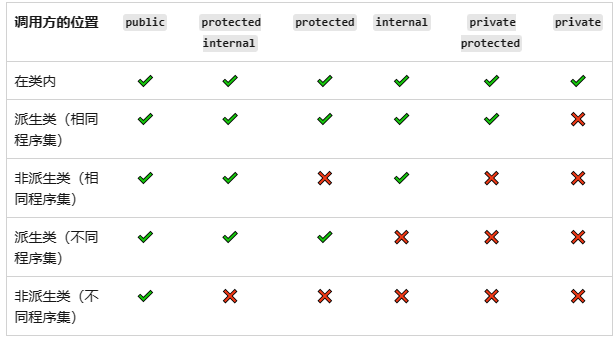
C#面试十问
1:C#中变量类型分为哪两种?它们的区别是什么?2:Class和Struct的区别?3:C#中类的修饰符和类成员的修饰符有哪些?4:面向对象的三个特征(特点)是什么?…...

Day 41 动态规划part03 : 343. 整数拆分 96.不同的二叉搜索树
96. 不同的二叉搜索树 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5示例 2: 输入:n 1…...

四轴飞行器的电池研究(MatlabSimulink仿真)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
准备HarmonyOS开发环境
引言 在开始 HarmonyOS 开发之前,需要准备好开发环境。本章将详细指导你如何安装 HarmonyOS SDK、配置开发环境、创建 HarmonyOS 项目。 目录 安装 HarmonyOS SDK 配置开发环境 创建 HarmonyOS 项目 总结 1. 安装 HarmonyOS SDK HarmonyOS SDK 是开发 Harmo…...
Java 面试 - Redis
Redis Redis 是基于键值对的非关系型数据库。Redis 拥有string、hash、list、set、zset等多种数据结构, redis具有惊人的读写性能, 其优秀的持久化机制是的它在断电和机械故障时也不会发生数据丢失, 可以用于热点数据存放, 还提供了键过期、发布订阅、食物、流水线、LUA脚本等多…...

【Go 基础篇】Go语言结构体之间的转换与映射
在Go语言中,结构体是一种强大的数据类型,用于定义和组织不同类型的数据字段。当我们处理复杂的数据逻辑时,常常需要在不同的结构体之间进行转换和映射,以便实现数据的转移和处理。本文将深入探讨Go语言中结构体之间的转换和映射技…...
Java 多线程系列Ⅳ(单例模式+阻塞式队列+定时器+线程池)
多线程案例 一、设计模式(单例模式工厂模式)1、单例模式2、工厂模式 二、阻塞式队列1、生产者消费者模型2、阻塞对列在生产者消费者之间的作用3、用标准库阻塞队列实现生产者消费者模型4、模拟实现阻塞队列 三、定时器1、标准库中的定时器2、模拟实现定时…...
将 ordinals 与 比特币智能合约集成 : 第 1 部分
将序数与比特币智能合约集成:第 1 部分 最近,比特币序数在区块链领域引起了广泛关注。 据称,与以太坊 ERC-721 等其他代币标准相比,Ordinals 的一个主要缺点是缺乏对智能合约的支持。 我们展示了如何向 Ordinals 添加智能合约功…...
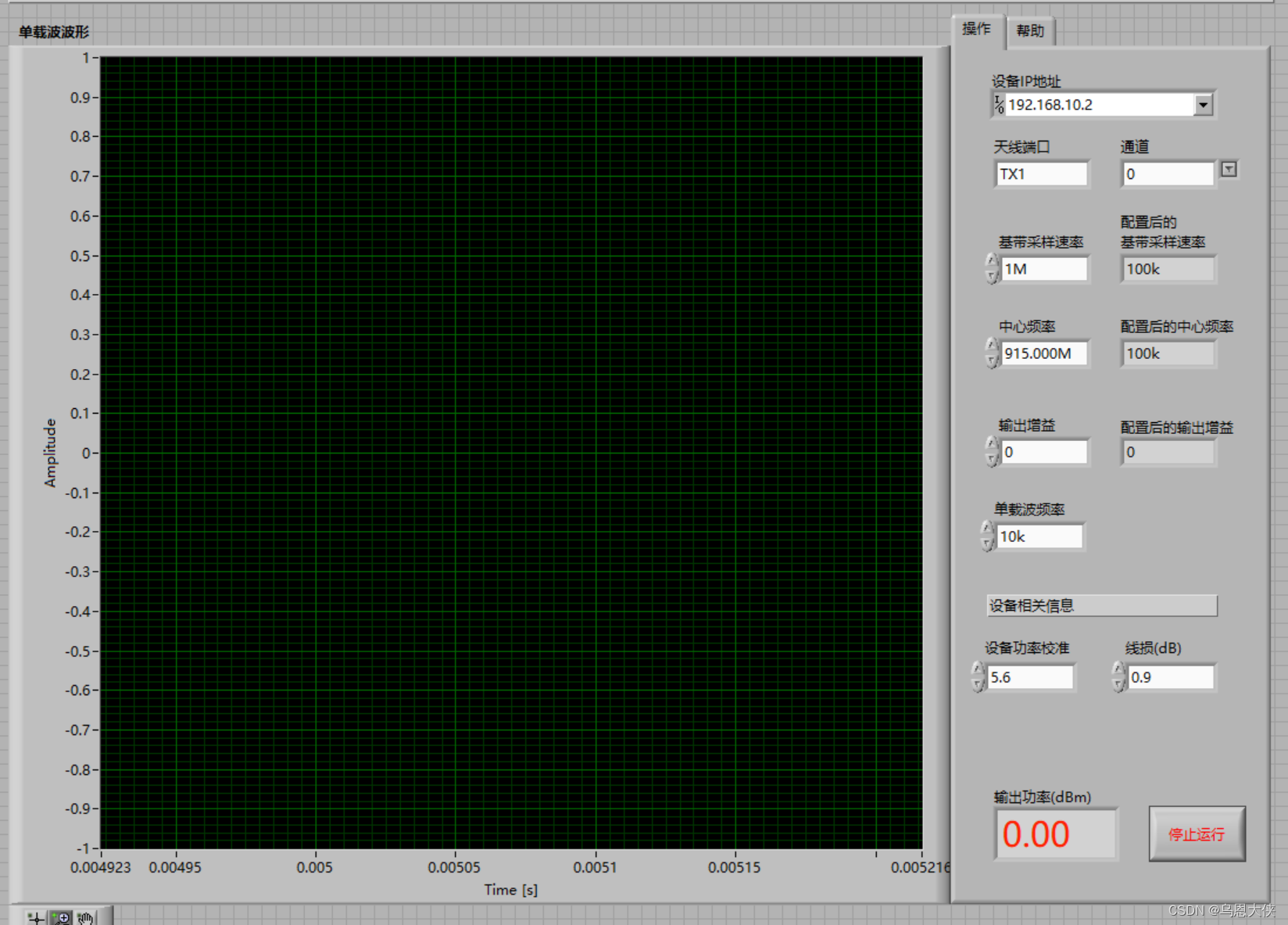
【USRP】集成化仪器系列1 :信号源,基于labview实现
USRP 信号源 1、设备IP地址:默认为192.168.10.2,请勿 修改,运行阶段无法修改。 2、天线输出端口是TX1,请勿修改。 3、通道:0 对应RF A、1 对应 RF B,运行 阶段无法修改。 4、中心频率:当需要…...
串行协议——USB驱动[基础]
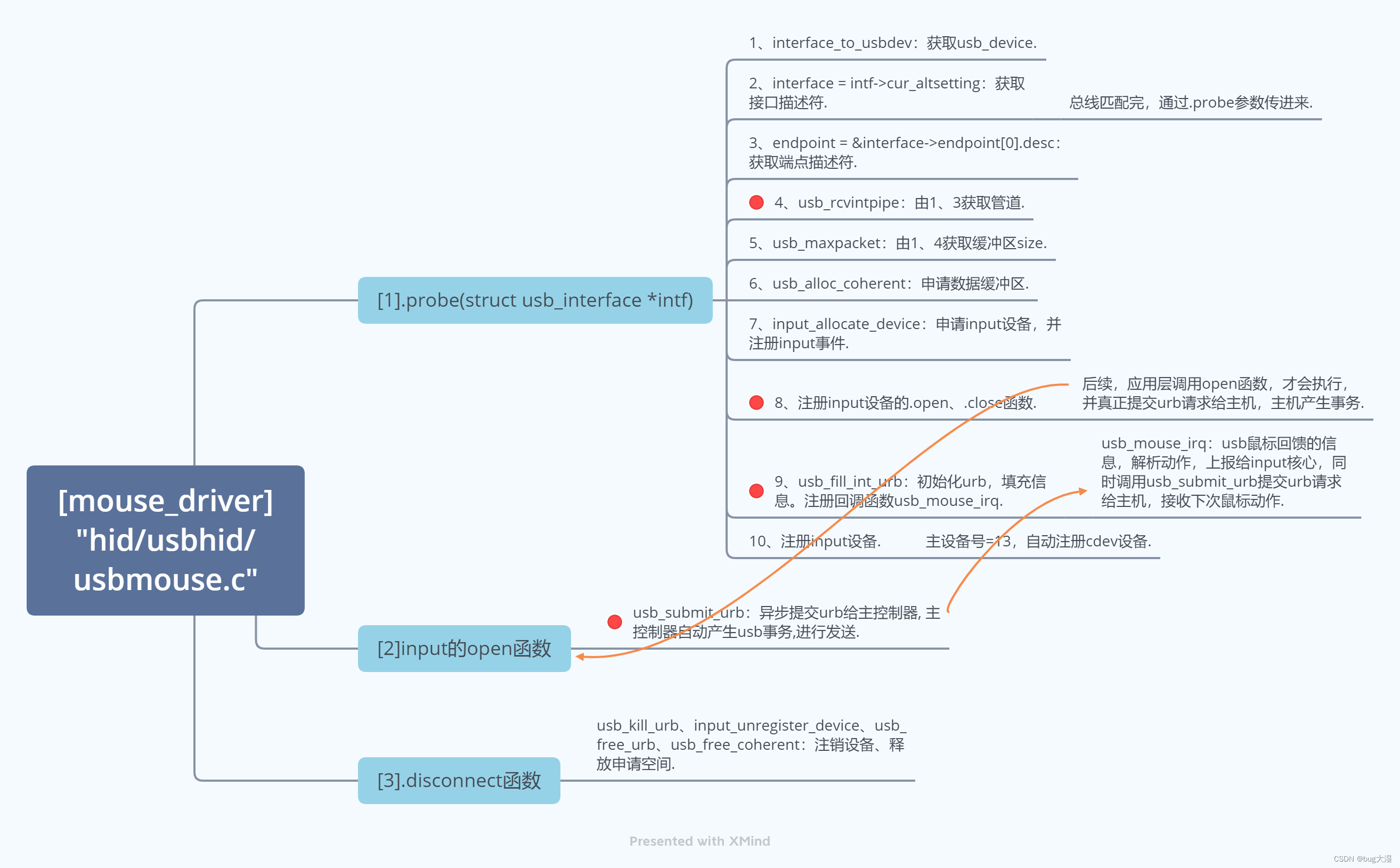
多年前的学习记录,整理整理。 一、USB协议基础 二、Linux内核USB驱动源码分析 USB中不同类型设备使用的 设备描述符(设备类\设备子类\设备协议) 配置不同,典型的以下几种:1)HID设备: Human Input Device人工输入设备, 如鼠标\键盘\游戏手柄等.2)CDC设备: Communi…...

健康舒适的超满意照明体验!SUKER书客SKY护眼台灯测评
健康舒适的超满意照明体验!SUKER书客SKY护眼台灯测评 2022年全国儿童青少年总体近视率为53.6%,其中6岁儿童为14.5%,小学生为36%,初中生为71.6%,高中生为81%,近视已成为当下人们遇到的比较普遍的眼健康问题…...

PID 算法
1.1 概述 比例(Proportion)积分(Integral)微分(Differential)控制器(PID控制器或三项控制器)是一种采用反馈的控制回路机制,广泛应用于工业控制系统和需要连续调制控制的…...
13.Redis 事务
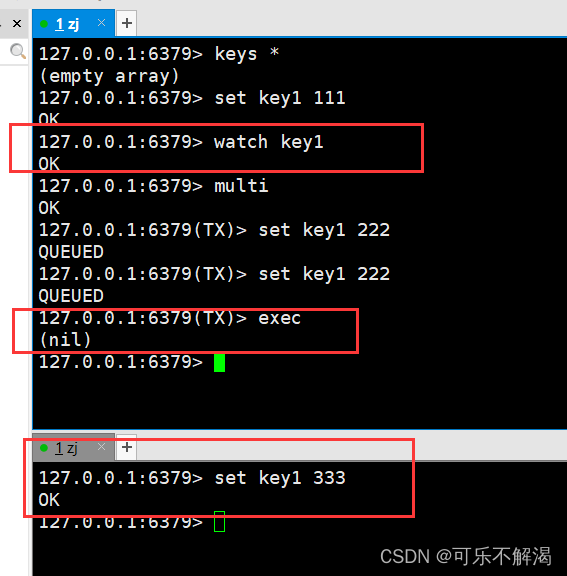
Redis 事务 redis 事务事务操作multi 开启事务exec 执行事务discard 放弃当前事务watchunwatch redis 事务 Redis 的事务和 MySQL 的事务概念上是类似的。 都是把⼀系列操作绑定成⼀组。 让这⼀组能够批量执⾏。 Redis 的事务和 MySQL 事务的区别: 弱化的原⼦性: 这里指的是 …...
)
李宏毅机器学习课程笔记(更新ing)
CNN 为什么AlphaGo可以用CNN?棋盘抽象成图片时需要注意什么? 首先图片有两个特点: 1,只观察局部就可以显示某种pattern,比如要得出一个鸟嘴的结论,只需要观察局部图片 2,某种pattern可以出现在图…...

SIP mini 对讲终端,带sip热点功能
SV-A10/SV-A10W SIP mini 对讲终端,带sip热点功能 SV-A10/SV-A10W 是专门针对行业用户需求研发的一款 SIP mini 对讲产品,外观小巧,功能 强大,集智能安防、音/视频对讲和广播功能于一体,性价比高。支持壁挂式安装/86…...

PHP中根据出生年月日计算年龄的封装函数
在 PHP 中,你可以使用以下函数来根据出生年月日计算年龄: 封装函数 function calculateAge($birthday) {$currentDate date(Y-m-d);$birthdayDate date(Y-m-d, strtotime($birthday));$age date_diff(date_create($currentDate), date_create($birt…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...