【面试经典150题】跳跃游戏Ⅱ
题目链接
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
1 <= nums.length <= 10^40 <= nums[i] <= 1000- 题目保证可以到达
nums[n-1]
这题借鉴了跳跃游戏的第一个解法的思路。
也就是找出并跳到[i,i+nums[i]]范围里索引+值最大的一个。
你每一步可以跳得更远才能更快得到达目的地。这就是每一步最优的贪心算法。
/*** @param {number[]} nums* @return {number}*/
var jump = function(nums) {if(nums.length===1){return 0;}let i = 0;let nextIndex;let maxVal = 0;let minStep=0;while (i + nums[i] < nums.length - 1) {for (let j = i + 1; j <= i + nums[i]; j++) {if (j + nums[j] > maxVal) {nextIndex = j;maxVal = j + nums[j];}}maxVal = 0;i = nextIndex;minStep++;}return minStep+1;
};
时间复杂度: O ( n ∗ M a x ( n u m s [ i ] ) ) O(n * Max(nums[i])) O(n∗Max(nums[i]))
空间复杂度: O ( 1 ) O(1) O(1)
上面的方法是主动寻找j+nums[j]最大值,我们可以维护一个最大可达位置maxReach来被动的求出最大值。
/*** @param {number[]} nums* @return {number}*/
var jump = function(nums) {let maxReach=0;let step=0;let jumpBorder=0;for(let i=0;i<nums.length-1;i++){maxReach=Math.max(maxReach,i+nums[i]);if(i===jumpBorder){step++;jumpBorder=maxReach;}}return step;
};
为什么是nums.length-1?
该算法阐述了一个过程:每次达到上一次跳跃的位置的可跳跃边界时,step++提前跳跃,跳到这一阶段的maxReach对应的位置,当然我们不需要知道这个位置,而i达到nums.length-1时,就不要再跳了,因为每次到达边界时我们就提前跳了,就不会漏一次。
相关文章:

【面试经典150题】跳跃游戏Ⅱ
题目链接 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i]i j < n 返回到达 nums[n…...

20230831-完成登录框的按钮操作,并在登录成功后进行界面跳转
登录框的按钮操作,并在登录成功后进行界面跳转 app.cpp #include "app.h" #include <cstdio> #include <QDebug> #include <QLineEdit> #include <QLabel> #include <QPainter> #include <QString> #include <Q…...

039 - sql逻辑操作符
前提: 做两个表employee和movie,用来练习使用; 表一:employee -- 创建表employee CREATE TABLE IF NOT EXISTS employee(id INT NOT NULL AUTO_INCREMENT,first_name VARCHAR(100) NOT NULL,last_name VARCHAR(100) NOT NULL,t…...

DbLInk使用
DbLInk介绍 DbLink是一种数据库连接技术,在不同的数据库之间进行数据传输和共享。它提供了一种透明的方法,让一个数据库访问另一个数据库的数据。 DbLink的优点是可以在多个数据库间实现数据共享,并且为不同数据库间的数据访问提供了便捷的…...

2.3 Vector 动态数组(迭代器)
C数据结构与算法 目录 本文前驱课程 1 C自学精简教程 目录(必读) 2 Vector<T> 动态数组(模板语法) 本文目标 1 熟悉迭代器设计模式; 2 实现数组的迭代器; 3 基于迭代器的容器遍历; 迭代器语法介绍 对迭…...
【ES6】Proxy的高级用法,实现一个生成各种 DOM 节点的通用函数dom
下面的例子则是利用get拦截,实现一个生成各种 DOM 节点的通用函数dom。 <body> </body><script>const dom new Proxy({}, {get(target, property) {return function(attrs {}, ...children) {const el document.createElement(property);for …...

气象站是什么设备?功能是什么?
气象站是一种用于测量和记录气象数据的设备。它通常是由各种传感器及其数据传输设备、固定设备和供电设备组成,可以测量风速、风向、温度、湿度、气压、降水量等气象要素,并将这些数据记录下来,以便进一步分析和研究。 气象站通常设置在广阔…...

227. 基本计算器 II Python
文章目录 一、题目描述示例 1示例 2示例 3 二、代码三、解题思路 一、题目描述 给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。 你可以假设给定的表达式总是有效的。所有中间结果将在 [-2^31, 2^31 - 1]的范围内…...

python中字典常用函数
字典常用函数 cmp(dict1,dict2) (已删除,直接用>,<,即可) 如果两个字典的元素相同返回0,如果字典dict1大于字典dict2返回1,如果字典dict1小于字典dict2返回-1。 先比较字典的长度,然后比较键&#x…...

leetcode88合并两个有序数组
题目: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终&…...

Ceph入门到精通-Nginx 大量请求 延迟优化
优化nginx以处理大量请求并减少延迟可以通过以下几种方法实现: 调整worker_processes和worker_connections参数:增加worker_processes值可以增加nginx的进程数量,提高并发处理能力。增加worker_connections参数的值可以增加每个worker进程可…...

Vulnstack----5、ATTCK红队评估实战靶场五
文章目录 一 环境搭建二 外网渗透三 内网信息收集3.1 本机信息收集3.2 域内信息收集 四 横向移动4.1 路由转发和代理通道4.2 抓取域用户密码4.3 使用Psexec登录域控4.4 3389远程登录 五、痕迹清理 一 环境搭建 1、项目地址 http://vulnstack.qiyuanxuetang.net/vuln/detail/7/ …...

QT 5.8
QT与Qt Creator,前者是框架,类似与MFC,而后者是QT的编译器,也可以使用Visual studio编辑,编译需要其他的 Index of /new_archive/qt/5.8/5.8.0...
AIGC+思维导图:提升你的学习与工作效率的「神器」
目录 一、产品简介 二、功能介绍 2.1 AI一句话生成思维导图 2.2百万模版免费用 2.3分屏视图,一屏读写 2.4团队空间,多人协作 2.5 云端跨平台化 2.6 免费够用,会员功能更强大 2.7 支持多种格式的导入导出 三、使用教程 3.1 使用AI…...
javaScript:DOM元素的获取(静态/动态获取)
目录 一.dom元素获取的意义与使用场景 使用场景(绝大多数js操作都需要dom操作) 总结/疑问解答! 二.DOM元素获取的常用方法(重点) 获取dom元素(动态) document.gerElementbyId() docume…...
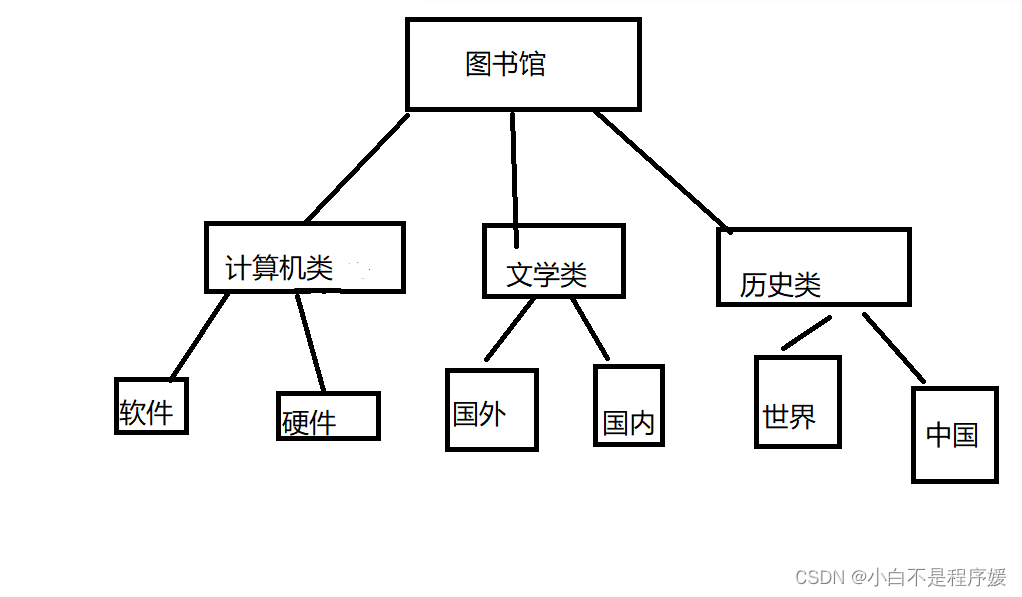
数据结构前言
一、什么是数据结构? 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。 上面是百度百科的定义,通俗的来讲数据结构就是数据元素集合与数据元素集合或者数据元素与数据元素之间的组成形式。 举个…...

Docker基于alpine带glibc的小型容器image
由于程序是C写的,gc编译,找了几个容器,生成比较小的是debianslim和ubuntu,生成后的大小分别为88MB,和91MB,还是太大了,于是想起一些小型容器如busybox或者alpine自己装glibc,但是试了…...
Nginx教程
Nginx教程 01-Nginx简介02-windows安装Nginx03-Nginx目录结构04-Linux安装Nginx05-linux下源码安装nginx06-linux下nginx配置07-在docker中安装nginx08-源码安装和yum安装的区别09-Nginx运行组和运行用户10-卸载nginx11-nginx的基本原理和架构12-nginx是如何处理请求的13-nginx…...

直播预约|哪吒汽车岳文强:OEM和Tier1如何有效对接网络安全需求
信息安全是一个防护市场。如果数字化程度低,数据量不够,对外接口少,攻击成本高,所获利益少,自然就没有什么攻击,车厂因此也不需要在防护上花费太多成本。所以此前尽管说得热闹,但并没有太多真实…...

hiveserver2经常挂断的原因
hiveserver2经常挂断的原因 HiveServer2 经常挂断可能有多种原因,以下是一些可能导致挂断的常见原因: 资源不足:HiveServer2 需要足够的内存和 CPU 资源来处理查询请求。如果资源不足,可能会导致 HiveServer2 挂断。请确保在配置…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
