227. 基本计算器 II Python
文章目录
- 一、题目描述
- 示例 1
- 示例 2
- 示例 3
- 二、代码
- 三、解题思路
一、题目描述
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-2^31, 2^31 - 1]的范围内。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1
输入:s = "3+2*2"
输出:7
示例 2
输入:s = " 3/2 "
输出:1
示例 3
输入:s = " 3+5 / 2 "
输出:5
提示:
1 <= s.length <= 3 * 10^5
s 由整数和算符 ('+', '-', '*', '/') 组成,中间由一些空格隔开
s 表示一个 有效表达式
表达式中的所有整数都是非负整数,且在范围 [0, 2^31 - 1] 内
题目数据保证答案是一个 32-bit 整数
二、代码
代码如下:
class Solution:def calculate(self, s: str) -> int:def is_operator(char):return char in "+-*/^"def infix_to_postfix(expression):def precedence(operator):precedence_dict = {'+': 1, '-': 1, '*': 2, '/': 2, '^': 3}return precedence_dict.get(operator, 0)def infix_to_postfix_internal(expression_tokens):output = []operator_stack = []for token in expression_tokens:if token.isnumeric(): # 如果是数字,直接添加到输出output.append(token)elif token == '(': # 如果是左括号,压入栈operator_stack.append(token)elif token == ')': # 如果是右括号,将栈顶的操作符弹出并添加到输出,直到遇到左括号while operator_stack and operator_stack[-1] != '(':output.append(operator_stack.pop())if operator_stack and operator_stack[-1] == '(':operator_stack.pop()elif is_operator(token): # 如果是操作符,处理操作符的优先级while (operator_stack andoperator_stack[-1] != '(' andprecedence(token) <= precedence(operator_stack[-1])):output.append(operator_stack.pop())operator_stack.append(token)while operator_stack: # 将栈中剩余的操作符全部添加到输出output.append(operator_stack.pop())return ' '.join(output)# 将输入的表达式字符串按空格分割成标记列表expression_tokens = expression.split()# 调用内部函数进行转换postfix_expression = infix_to_postfix_internal(expression_tokens)return postfix_expressiondef add_spaces_to_infix(expression):operators = "+-*/^"result = []for char in expression:if char in operators or char in "()":result.append(f" {char} ")else:result.append(char)return ''.join(result)infix_expression = s.replace(" ", "")print(infix_expression)spaced_infix_expression = add_spaces_to_infix(infix_expression)print(spaced_infix_expression)postfix_expression = infix_to_postfix(spaced_infix_expression)print("中缀表达式:", spaced_infix_expression)print("后缀表达式:", postfix_expression)stack = []for token in postfix_expression.split():if token.isnumeric():stack.append(int(token))elif is_operator(token):operand2 = stack.pop()operand1 = stack.pop()if token == '+':result = operand1 + operand2elif token == '-':result = operand1 - operand2elif token == '*':result = operand1 * operand2elif token == '/':if operand2 == 0:raise ValueError("Division by zero")result = int(operand1 / operand2)stack.append(result)print(int(stack[0]))return int(stack[0])
三、解题思路
本题本质是要求通过字符串来计算表达式,且不能直接使用eval方法对字符串直接进行转化计算。本题解题思路为:将字符串(前缀表达式)转化为后缀表达式,然后通过计算后缀表达式得到结果。
① 因为涉及到字符可能会出现2位数及其以上的情况,如果之间转化为后缀表达式,则会导致数字连接到一块,所以需要对数字和运算符进行分隔,将表达式转化为如下格式:“12+4/5” => “12 + 4 / 5”
② 转化为后缀表达式,当遇到2位数及以上的数字时,需要将其看做是一个数,用空格分隔不同数。例如:
中缀表达式: 12 + 4 / 5
后缀表达式: 12 4 5 / +
不同的数之间用空格分开
③ 计算后缀表达式,找第一个运算符,向左找最近的2个数进行计算,重复这一过程,最后得到一个值返回即可。
相关文章:

227. 基本计算器 II Python
文章目录 一、题目描述示例 1示例 2示例 3 二、代码三、解题思路 一、题目描述 给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。 你可以假设给定的表达式总是有效的。所有中间结果将在 [-2^31, 2^31 - 1]的范围内…...

python中字典常用函数
字典常用函数 cmp(dict1,dict2) (已删除,直接用>,<,即可) 如果两个字典的元素相同返回0,如果字典dict1大于字典dict2返回1,如果字典dict1小于字典dict2返回-1。 先比较字典的长度,然后比较键&#x…...

leetcode88合并两个有序数组
题目: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终&…...

Ceph入门到精通-Nginx 大量请求 延迟优化
优化nginx以处理大量请求并减少延迟可以通过以下几种方法实现: 调整worker_processes和worker_connections参数:增加worker_processes值可以增加nginx的进程数量,提高并发处理能力。增加worker_connections参数的值可以增加每个worker进程可…...

Vulnstack----5、ATTCK红队评估实战靶场五
文章目录 一 环境搭建二 外网渗透三 内网信息收集3.1 本机信息收集3.2 域内信息收集 四 横向移动4.1 路由转发和代理通道4.2 抓取域用户密码4.3 使用Psexec登录域控4.4 3389远程登录 五、痕迹清理 一 环境搭建 1、项目地址 http://vulnstack.qiyuanxuetang.net/vuln/detail/7/ …...

QT 5.8
QT与Qt Creator,前者是框架,类似与MFC,而后者是QT的编译器,也可以使用Visual studio编辑,编译需要其他的 Index of /new_archive/qt/5.8/5.8.0...
AIGC+思维导图:提升你的学习与工作效率的「神器」
目录 一、产品简介 二、功能介绍 2.1 AI一句话生成思维导图 2.2百万模版免费用 2.3分屏视图,一屏读写 2.4团队空间,多人协作 2.5 云端跨平台化 2.6 免费够用,会员功能更强大 2.7 支持多种格式的导入导出 三、使用教程 3.1 使用AI…...
javaScript:DOM元素的获取(静态/动态获取)
目录 一.dom元素获取的意义与使用场景 使用场景(绝大多数js操作都需要dom操作) 总结/疑问解答! 二.DOM元素获取的常用方法(重点) 获取dom元素(动态) document.gerElementbyId() docume…...
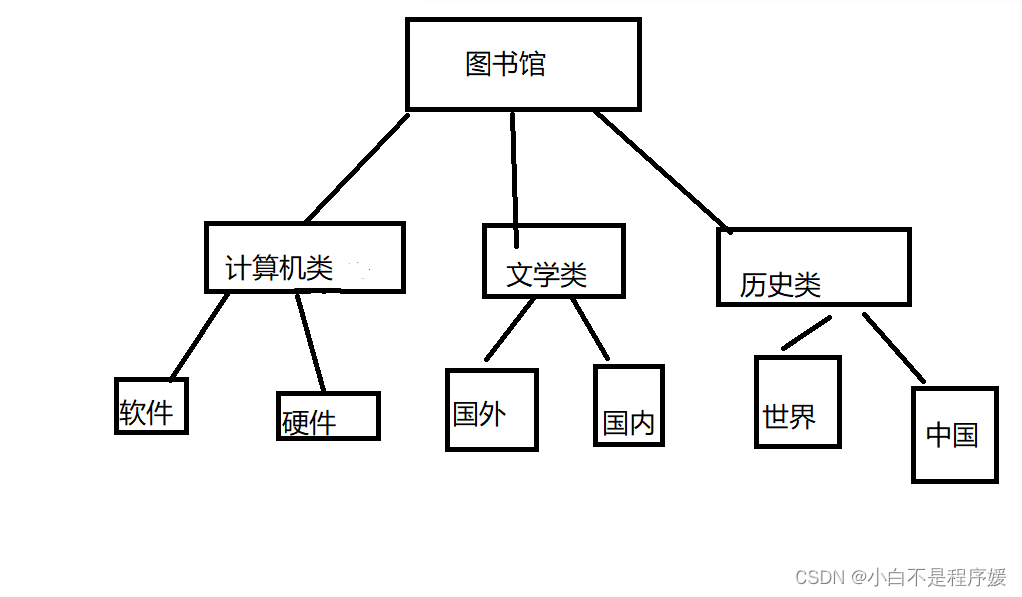
数据结构前言
一、什么是数据结构? 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。 上面是百度百科的定义,通俗的来讲数据结构就是数据元素集合与数据元素集合或者数据元素与数据元素之间的组成形式。 举个…...

Docker基于alpine带glibc的小型容器image
由于程序是C写的,gc编译,找了几个容器,生成比较小的是debianslim和ubuntu,生成后的大小分别为88MB,和91MB,还是太大了,于是想起一些小型容器如busybox或者alpine自己装glibc,但是试了…...
Nginx教程
Nginx教程 01-Nginx简介02-windows安装Nginx03-Nginx目录结构04-Linux安装Nginx05-linux下源码安装nginx06-linux下nginx配置07-在docker中安装nginx08-源码安装和yum安装的区别09-Nginx运行组和运行用户10-卸载nginx11-nginx的基本原理和架构12-nginx是如何处理请求的13-nginx…...

直播预约|哪吒汽车岳文强:OEM和Tier1如何有效对接网络安全需求
信息安全是一个防护市场。如果数字化程度低,数据量不够,对外接口少,攻击成本高,所获利益少,自然就没有什么攻击,车厂因此也不需要在防护上花费太多成本。所以此前尽管说得热闹,但并没有太多真实…...

hiveserver2经常挂断的原因
hiveserver2经常挂断的原因 HiveServer2 经常挂断可能有多种原因,以下是一些可能导致挂断的常见原因: 资源不足:HiveServer2 需要足够的内存和 CPU 资源来处理查询请求。如果资源不足,可能会导致 HiveServer2 挂断。请确保在配置…...

openeuler 23.03 安装mysql 8.X
遇到一堆问题:直接从mysql官下载,都不行。下列是失败的: mysql80-community-release-el8-1.noarch.rpm mysql-8.0.34-1.el8.x86_64.rpm-bundle.tar mysql-8.1.0-1.el9.x86_64.rpm-bundle.tar 后来想从openeuler下载应该靠谱:ht…...

网络安全—0基础学习笔记(黑客)
一、前言 1.这是一条坚持的道路,三分钟的热情可以放弃往下看了. 2.多练多想,不要离开了教程什么都不会了.最好看完教程自己独立完成技术方面的开发. 3.有时多 google,baidu,我们往往都遇不到好心的大神,谁会无聊天天给你做解答. 4.遇到实在搞不懂的,可以先放放,以后再来解决. …...

react HashRouter 与 BrowserRouter 的区别及使用场景
一、简介 在单页面应用中,如何在切换页面后,不刷新浏览器呢?为了解决这个问题,有两种方法,就是hash路由模式、history路由模式,而 react router 的两种路由就是使用这两种路由模式。 二、区别 HashRouter…...

痞子衡嵌入式:恩智浦i.MX RT1xxx系列MCU硬件那些事(2.3)- 串行NOR Flash下载算法(J-Link工具篇)
https://www.cnblogs.com/henjay724/p/13770137.html 大家好,我是痞子衡,是正经搞技术的痞子。今天痞子衡给大家介绍的是J-Link工具下i.MXRT的串行NOR Flash下载算法设计。 在i.MXRT硬件那些事系列之《在串行NOR Flash XIP调试原理》一文中,痞…...
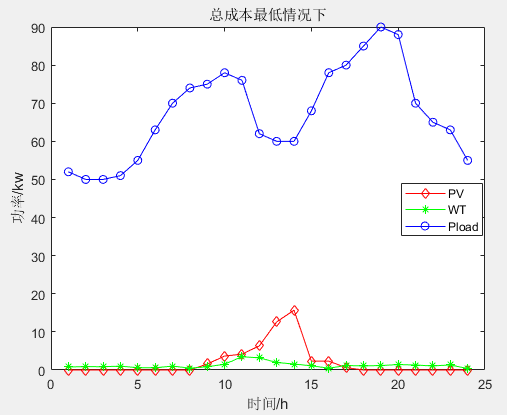
多目标应用:基于多目标向日葵优化算法(MOSFO)的微电网多目标优化调度MATLAB
一、微网系统运行优化模型 参考文献: [1]李兴莘,张靖,何宇,等.基于改进粒子群算法的微电网多目标优化调度[J].电力科学与工程, 2021, 37(3):7 二、多目标向日葵优化算法 多目标向日葵优化算法(Multi-objective sunflower optimization,MOS…...

智能安全科技,Vatee万腾为您服务
在智能科技的引领下,Vatee万腾将为您点亮投资之路,助您在金融市场中抓住机遇,实现财务目标。作为一家融合科技与投资的先锋平台,Vatee万腾致力于为投资者提供智能化的投资方案和支持。 Vatee万腾以其先进的智能科技为基础…...

Scala中的类型检查和转换,以及泛型,scala泛型的协变和逆变
Scala中的类型检查和转换,以及泛型 类型检查和转换 说明 (1) obj.isInstanceOf[T]:判断 obj 是不是T 类型。 (2) obj.asInstanceOf[T]:将 obj 强转成 T 类型。 (3) cla…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
