【算法】函数渐近的界基础知识及定理
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!!
主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步!
🔥c++系列专栏:C/C++零基础到精通 🔥给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ

c语言内容💖:
专栏:c语言之路重点知识整合
【c语言】全部知识点总结
目录
- 一、5种渐近意义下的符号
- 1.渐近上界——大 O 符号
- 2.渐近下界——大 Ω 符号
- 3.非渐近紧确上界——小 o 符号
- 4.非渐近紧确上界——小 ω 符号
- 5.同界—— Θ 符号
- 图解
- 二、有关函数渐近的界的定理
- 三、取整函数
- 总结
函数渐近的界可以用来表示函数的边界或范围的集合
可以分为:
- 上界
- 同界
- 下界
一、5种渐近意义下的符号
1.渐近上界——大 O 符号
定义:
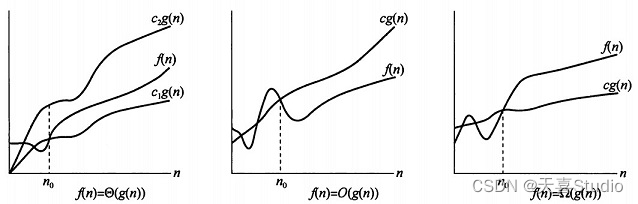
设 f 和 g是定义域为自然数集N上的函数。若存在正数 c 和 n0 ,使得 对一切 n > n0有 0 <f(n) < cg(n)成立, 则称f(n) 的渐近的上界是 g(n),记作 f (n) = O(g(n))
例子:
设f(n) = n2 + n,则
f(n)=O(n2),取 c = 2 ,n0 =1 即可
f(n)=O(n3),取 c = 1 ,n0 =2 即可
-
f (n) = O(g(n)) ,f(n)的阶不高于g(n)的阶.
-
可能存在多个正数c,只要指出一个即可.
-
对前面有限个值可以不满足不等式.
-
常函数可以写作O(1).
上界的阶越低,评估越准确
大O符号可以看作是<=号-------时间复杂度的最坏情况T(max)
2.渐近下界——大 Ω 符号
定义:
设 f 和 g是定义域为自然数集N上的函数。若存在正数 c 和 n0,使得对一切 n > n0有 0 < cg(n) <f(n)成立, 则称f(n) 的渐近的下界是 g(n),记作 f (n) = Ω(g(n))
例子:
设f(n) = n2 + n,则
f(n) = Ω (n2), 取 c = 1, n0 =1即可
f(n) = Ω(100n), 取 c=1/100, n0 =1即可
-
f (n)=Ω (g(n)),f(n)的阶不低于g(n)的阶.
-
可能存在多个正数c,指出一个即可.
-
对前面有限个 n 值可以不满足上述不等式.
下界的阶越高,评估越准确
大 Ω 符号可以看作是>=号-------时间复杂度的最好情况T(min)
3.非渐近紧确上界——小 o 符号
定义:
设 f 和g是定义域为自然数集 N上的函数。若对于任意正数 c 都存在 n0,
使得对一切 n > n0有 <f(n) < cg(n)成立, 则记作f (n) = o(g(n))
例子:
f(n)=n2+n,则
f(n)=o(n3)
c>1显然成立,因为n2+n<cn3(n0=2)
任给1>c >0, 取 n0 >「2/c] 即可。因为cn > cn0 > 2 (当n > n0 ) n2+n < 2n2 < cn3
- f (n) = o(g(n)) ,f(n)的阶低于g(n)的阶
- 对不同正数c, n0不一样. c越小n0越大
- 对前面有限个 n 值可以不满足不等式
如果 l i m n → ∞ \underset{n → ∞}{lim} n→∞lim f (n) / g(n)=0,那么f(n) = o(g(n))
小 o 符号可以看作是<号`
4.非渐近紧确上界——小 ω 符号
定义:
设 f 和 g是定义域为自然数集 N上的函数。若对于任意正数 c 都存在 n0 ,使 得对一切 n > n0有
0 < cg(n) <f(n) 成立, 则记作f (n) = ω (g(n))
如果 l i m n → ∞ \underset{n → ∞}{lim} n→∞lim f (n) / g(n)=∞,那么f(n) = ω (g(n))
小 ω 符号可以看作是>号`
5.同界—— Θ 符号
定义:
若f (n) = O (g(n)) 且f (n) = Ω(g(n)), 则记作f (n) = Θ(g(n))
例子:
f(n) =n2+ n, g(n) =100n2 ,那么有f(n)=Θ(g(n))
-
f(n) 的阶与 g(n) 的阶相等.
-
对前面有限个n 值可以不满足条件.
如果 l i m n → ∞ \underset{n → ∞}{lim} n→∞lim f (n) / g(n)存在且等于某个常数,那么f(n) = Θ (g(n))
图解
二、有关函数渐近的界的定理



三、取整函数


总结
-
估计函数的阶的方法:
计算极限
阶具有传递性 -
对数函数的阶低于幂函数的阶,多项 式函数的阶低于指数函数的阶.
-
算法的时间复杂度是各步操作时间之 和,在常数步的情况下取最高阶的函 数即可.

| 大家的点赞、收藏、关注将是我更新的最大动力! 欢迎留言或私信建议或问题。 |
| 大家的支持和反馈对我来说意义重大,我会继续不断努力提供有价值的内容!如果本文哪里有错误的地方还请大家多多指出(●'◡'●) |
相关文章:

【算法】函数渐近的界基础知识及定理
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c系列专栏:C/C零基础到精通 🔥 给大…...

stable diffusion实践操作-writing
文章目录 前言一、优点1.1、免费开源1.2、拥有强大的外接模型 二、组成要素2.1 底模2.2 风格2.3 提示词2.4 参数配置 三、生图原理四、下载链接 实践正文一、安装1.1 电脑硬件配置查看1.2 安装本地版本的stable diffusion1.3 SD使用教程 二、模型介绍与下载2.1大模型2.2 Lora模…...
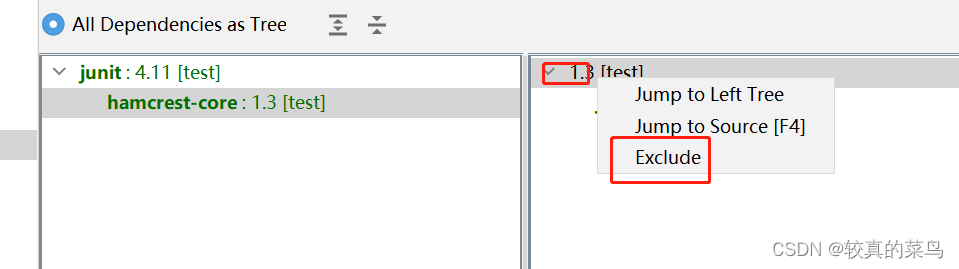
idea查找maven所有依赖
文章目录 idea自带的依赖结构图idea安装maven helper插件 idea自带的依赖结构图 缺点是只有依赖,没有版本 idea安装maven helper插件 settings–>plugins–>搜索maven helper并安装 安装后打开pom.xml文件会有依赖解析 勾选conflict就是有冲突的依赖选中…...
【业务功能篇97】微服务-springcloud-springboot-电商购物车模块-获取当前登录用户的购物车信息
购物车功能 一、购物车模块 1.创建cart服务 我们需要先创建一个cart的微服务,然后添加相关的依赖,设置配置,放开注解。 <dependencies><dependency><groupId>com.msb.mall</groupId><artifactId>mall-commo…...

Shell常用的几个正则表达式:[:alnum:], [:alpha:], [:upper:], [:lower:], [:digit:] 认知
一:通配符命令简介: 匹配符合相关条件的符号,匹配文件名查找。 通配符类型: *:匹配任意长度的任意字符 ?:匹配任意单个字符 []:匹配指定范围内的任意单个字符 [^]:匹配指…...
简单的爬虫代码 爬(豆瓣电影)
路漫漫其修远兮,吾将上下而求索 这次写一个最简单的python爬虫代码,也是大多教程第一次爬取的,代码里面有个别的简单介绍,希望能加深您对python爬虫的理解。 本次爬取两个网页数据 一 爬取的网站 豆瓣电影 爬取网页中的&#…...
微服务之架构演变
随着互联网的发展,网站应用规模不断扩大,网站架构随之不断演变,演变历史大致分为单体应用架构-垂直应用架构-分布式架构-SOA架构-微服务架构-云原生架构 架构演变 单体应用架构 以前网站流量小,只需要一个应用就可以把所有功能…...
)
面试问题记录一 --- C++(Qt方向)
以下是我于2023年6~7月间换工作时遇到的面试题目,有需要的小伙伴可以参考下。约100个题目。 1 C和C++的区别 1) 文件区别:C源文件后缀 .c;C++源文件后缀 .cpp 2) 返回值: C默认返回int型;C++ 若无返回值,必须指定为void 3) 参数列表:C默认接收多个…...
测试提取图像的特征点和聚类中心)
使用词袋模型(BoW)测试提取图像的特征点和聚类中心
文章目录 环境配置代码测试 环境配置 (1) 导入opencv,参考链接 https://blog.csdn.net/Aer_7z/article/details/132612369(2) 安装numpy 激活虚拟环境的前提下,输入: pip install numpy(3) 安装sklearn 激活虚拟环境的前提下,输…...
利用vba处理Excel表格数据实现键值转化,适用于将编码转化成对应的文本
最近遇到了一个甲方需要提供系统登录的用户名单和对应的角色权限内容。无奈直接从数据库导出的数据对应的都是编码,没有转成中文,想着偷个懒能不能直接用Excel直接转,网上看了一下有修改单元格格式的,但需要编码是2到3个。多的就用…...
IntelliJ IDEA(Windows 版)的所有快捷键
🪁🍁 希望本文能够给您带来一定的帮助🌸文章粗浅,敬请批评指正!🍁🐥 大家好 本文参考了 IntelliJ IDEA 的官网,列举了IntelliJ IDEA(Windows 版)的所有快捷…...

文件上传漏洞全面渗透姿势
0x00 文件上传场景 (本文档只做技术交流) 文件上传的场景真的随处可见,不加防范小心,容易造成漏洞,造成信息泄露,甚至更为严重的灾难。 比如某博客网站评论编辑模块,右上角就有支持上传图片的功能,提交带…...
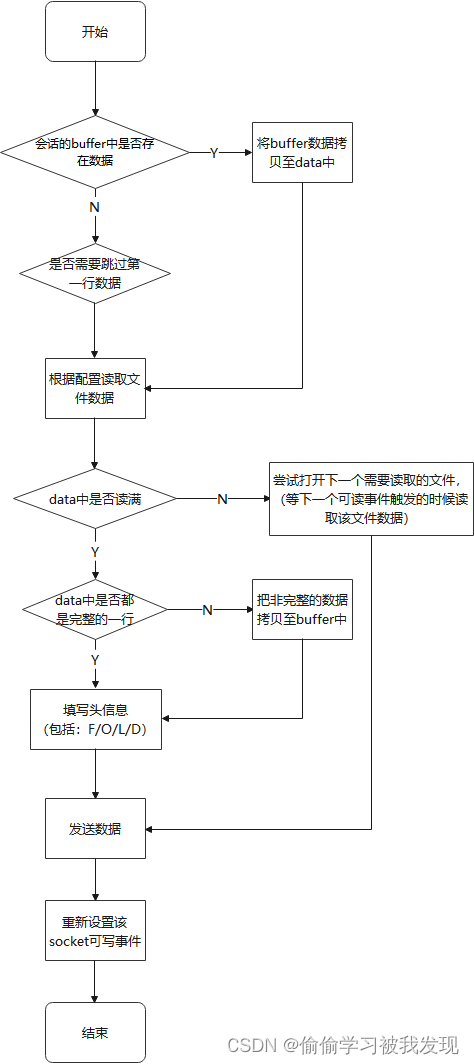
GreenPlum的gpfdist使用与原理流程分析
一、简介 GreenPlum 的数据导入功能作为对数据源的一种扩充,数据导入的方式有: 1、insert 该方式通过 sql 语句,把数据一条一条插入至表中。这种方式,不仅读取数据慢(一条一条读取),且数据需要…...
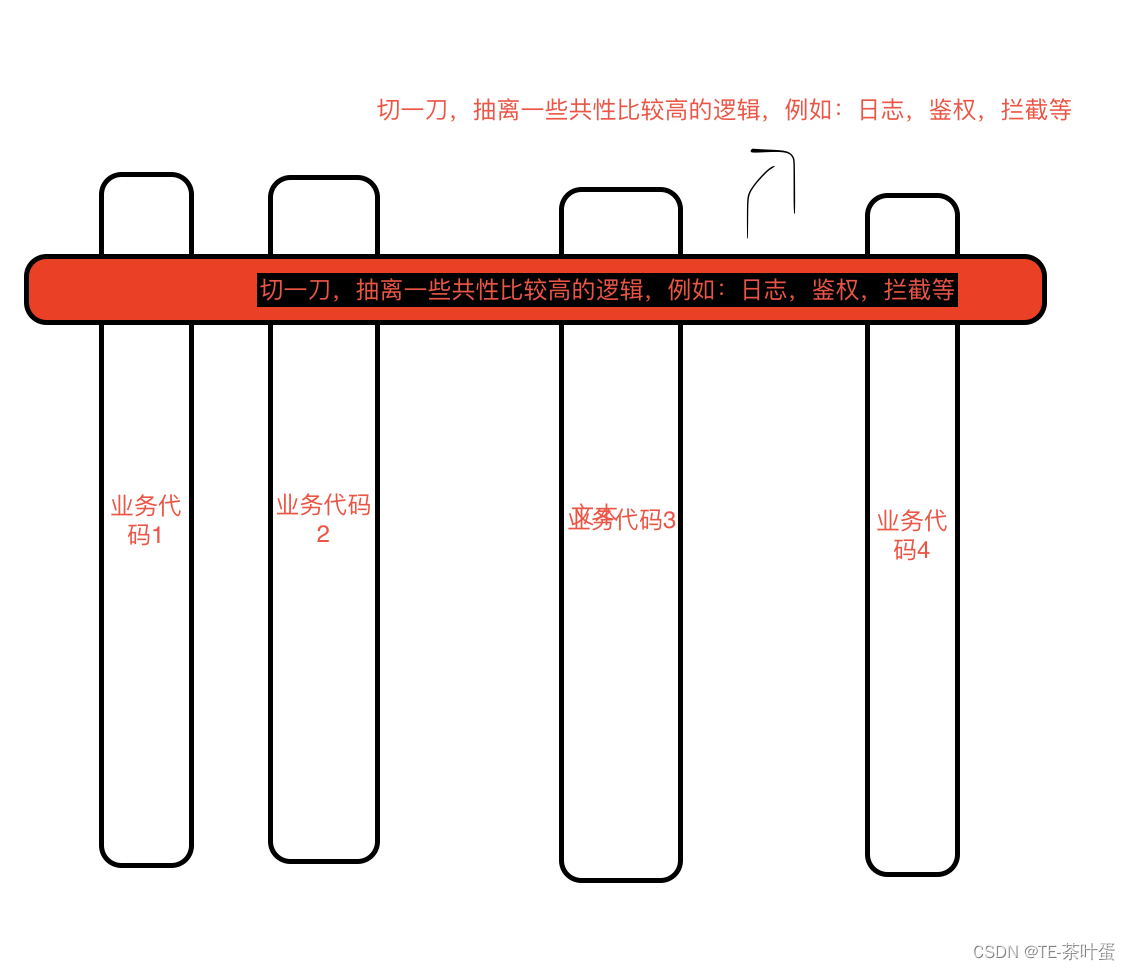
Spring AOP与静态代理/动态代理
文章目录 一、代理模式静态代理动态代理代理模式与AOP 二、Spring AOPSping AOP用来处理什么场景jdk 动态代理cglib 动态代理面试题:讲讲Spring AOP的原理与执行流程 总结 一、代理模式 代理模式是一种结构型设计模式,它允许对象提供替代品或占位符&…...
【LeetCode算法系列题解】第51~55题
CONTENTS LeetCode 51. N 皇后(困难)LeetCode 52. N 皇后 II(困难)LeetCode 53. 最大子序和(中等)LeetCode 54. 螺旋矩阵(中等)LeetCode 55. 跳跃游戏(中等) …...
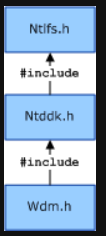
驱动开发错误汇编
本博文将会不定期更新。以便记录我的驱动开发生涯中的一些点点滴滴的技术细节和琐事。 1. link阶段找不到导出函数 比如"LNK2019 无法解析的外部符号 _FltCreateCommunicationPort32"。 出现这种情况的原因是,驱动的编译环境忽略了所有的默认库&#x…...
知识图谱项目实践
目录 步骤 SpaCy Textacy——Text Analysis for Cybersecurity Networkx Dateparser 导入库 写出页面的名称 编辑 自然语言处理 词性标注 可能标记的完整列表 依存句法分析(Dependency Parsing,DEP) 可能的标签完整列表 实例理…...

stable diffusion实践操作-提示词-人物属性
系列文章目录 stable diffusion实践操作-提示词 文章目录 系列文章目录前言一、提示词汇总1.1 人物属性11.2 人物属性2 前言 本文主要收纳总结了提示词-人物属性。 一、提示词汇总 1.1 人物属性1 角色类型人物身材胸部头发-发型头发-发色[女仆][霊烏路空][大腿][乳房][呆毛…...

RabbitMQ的安装和配置
将RabbitMQ文件夹传到linux根目录 开启管理界面及配置...

WebRTC 日志
WebRTC 日志 flyfish WebRTC支持的日志等级 // // The meanings of the levels are: // LS_VERBOSE: This level is for data which we do not want to appear in the // normal debug log, but should appear in diagnostic logs. // LS_INFO: Chatty level used in de…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
