2023年高教社杯数学建模思路 - 案例:粒子群算法
文章目录
- 1 什么是粒子群算法?
- 2 举个例子
- 3 还是一个例子
- 算法流程
- 算法实现
- 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 什么是粒子群算法?
粒子群算法(Particle Swarm Optimization,PSO)是一种模仿鸟群、鱼群觅食行为发展起来的一种进化算法。其概念简单易于编程实现且运行效率高、参数相对较少,应用非常广泛。粒子群算法于1995年提出,距今(2019)已有24年历史。
粒子群算法中每一个粒子的位置代表了待求问题的一个候选解。每一个粒子的位置在空间内的好坏由该粒子的位置在待求问题中的适应度值决定。每一个粒子在下一代的位置有其在这一代的位置与其自身的速度矢量决定,其速度决定了粒子每次飞行的方向和距离。在飞行过程中,粒子会记录下自己所到过的最优位置 P,群体也会更新群体所到过的最优位置G 。粒子的飞行速度则由其当前位置、粒子自身所到过的最优位置、群体所到过的最优位置以及粒子此时的速度共同决定。

2 举个例子
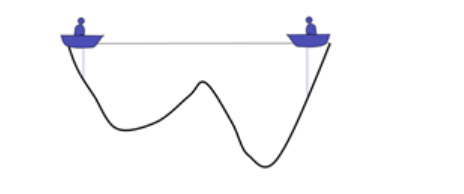
在一个湖中有两个人他们之间可以通信,并且可以探测到自己所在位置的最低点。初始位置如上图所示,由于右边比较深,因此左边的人会往右边移动一下小船。
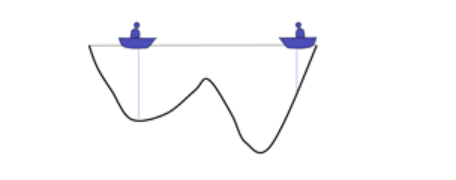
现在左边比较深,因此右边的人会往左边移动一下小船
一直重复该过程,最后两个小船会相遇
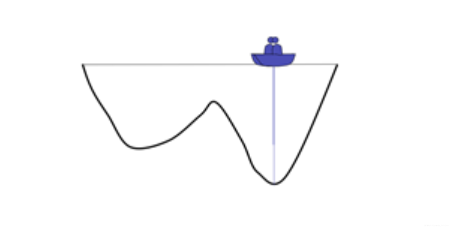
得到一个局部的最优解
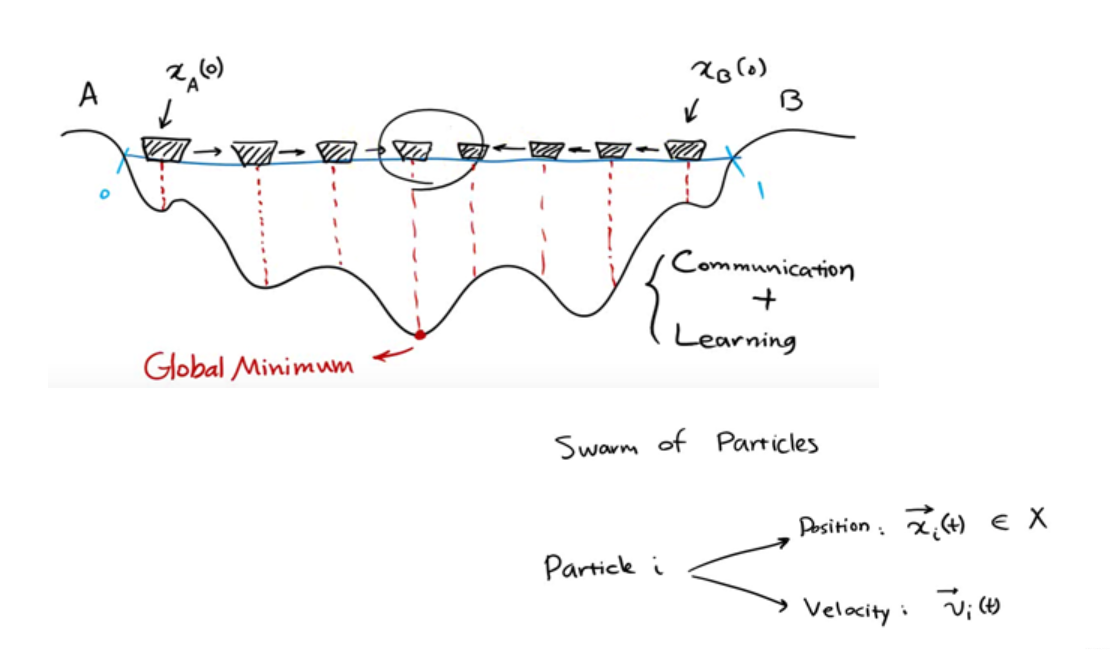 将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
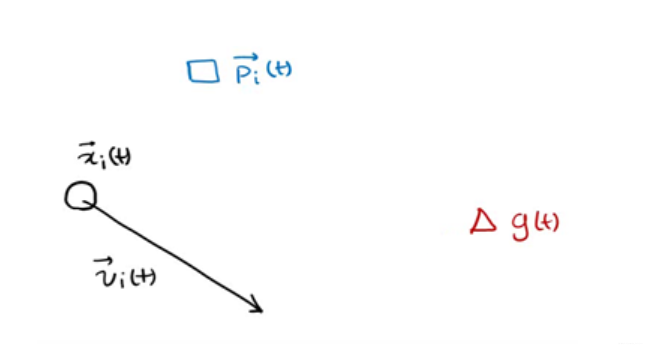
p(t)为在t时刻x个体的自己的最优解,g(t)为在t时刻所有个体的最优解,v(t)为个体在t时刻的方向,x(t)为个体在t时刻的位置
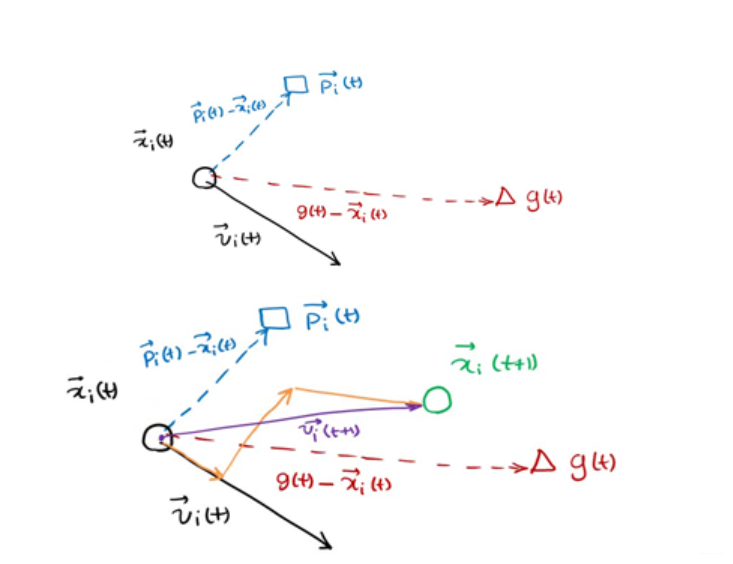
下一个位置为上图所示由x,p,g共同决定了
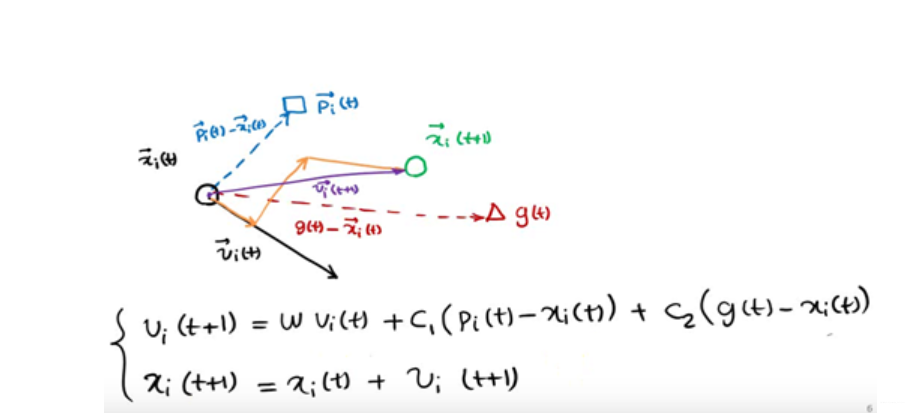
种群中的粒子通过不断地向自身和种群的历史信息进行学习,从而可以找到问题的最优解。
3 还是一个例子
粒子群算法是根据鸟群觅食行为衍生出的算法。现在,我们的主角换成是一群鸟。

小鸟们的目标很简单,要在这一带找到食物最充足的位置安家、休养生息。它们在这个地方的搜索策略如下:
1. 每只鸟随机找一个地方,评估这个地方的食物量。
2. 所有的鸟一起开会,选出食物量最多的地方作为安家的候选点G。
3. 每只鸟回顾自己的旅程,记住自己曾经去过的食物量最多的地方P。
4. 每只鸟为了找到食物量更多的地方,于是向着G飞行,但是呢,不知是出于选择困难症还是对P的留恋,或者是对G的不信任,小鸟向G飞行时,时不时也向P飞行,其实它自己也不知道到底是向G飞行的多还是向P飞行的多。
5. 又到了开会的时间,如果小鸟们决定停止寻找,那么它们会选择当前的G来安家;否则继续2->3->4->5来寻找它们的栖息地。
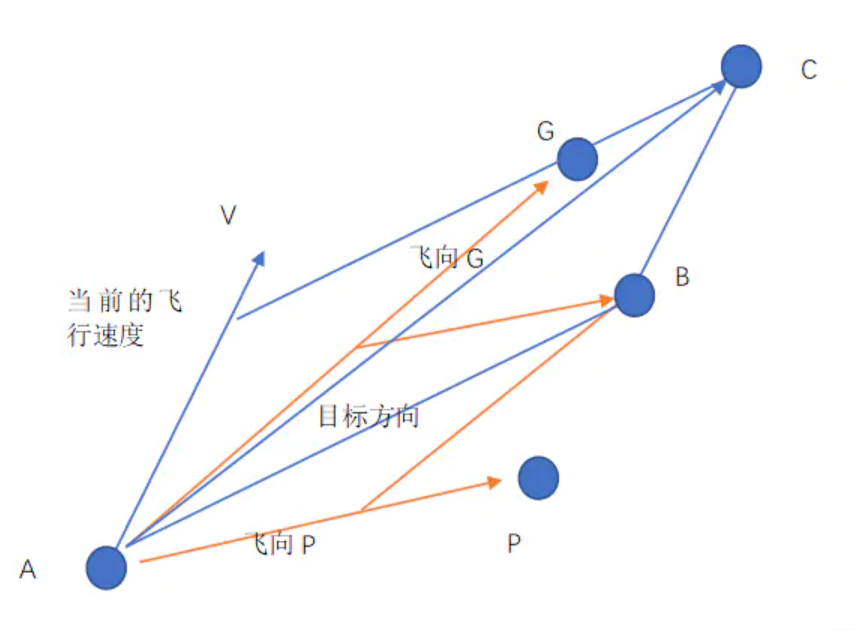
上图描述的策略4的情况,一只鸟在点A处,点G是鸟群们找到过的食物最多的位置,点P是它自己去过的食物最多的地点。V是它现在的飞行速度(速度是矢量,有方向和大小),现在它决定向着P和G飞行,但是这是一只佛系鸟,具体飞多少随缘。如果没有速度V,它应该飞到B点,有了速度V的影响,它的合速度最终使它飞到了点C,这里是它的下一个目的地。如果C比P好那么C就成了下一次的P,如果C比G好,那么就成了下一次的G。
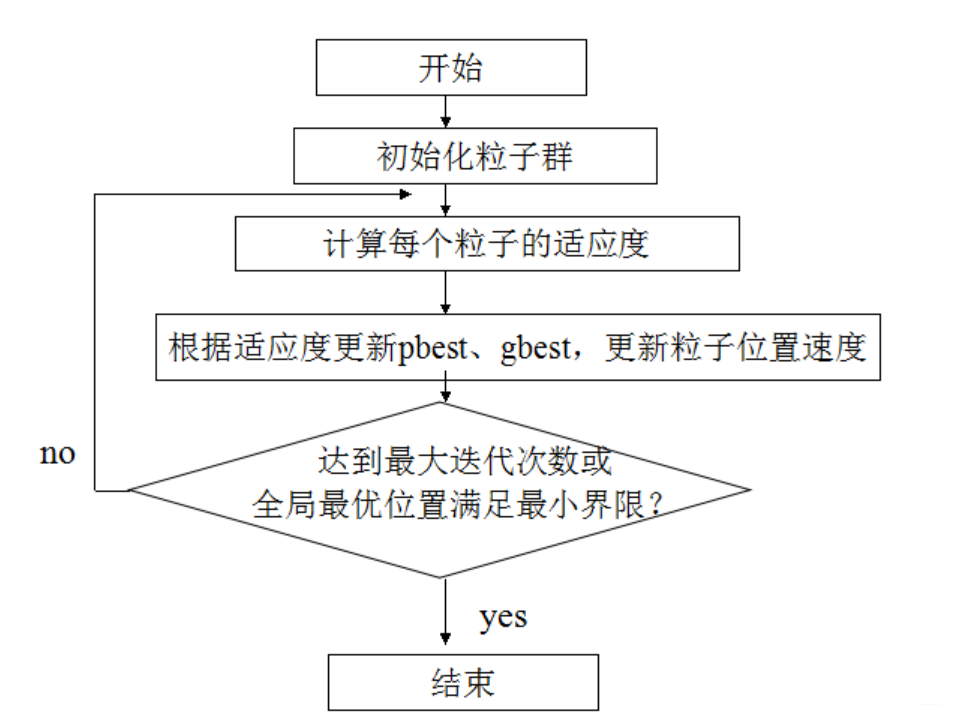
算法流程
算法实现
这里学长用python来给大家演示使用粒子群解函数最优解
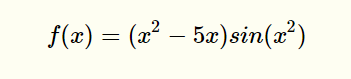
import numpy as np
import matplotlib.pyplot as plt
import random# 定义“粒子”类
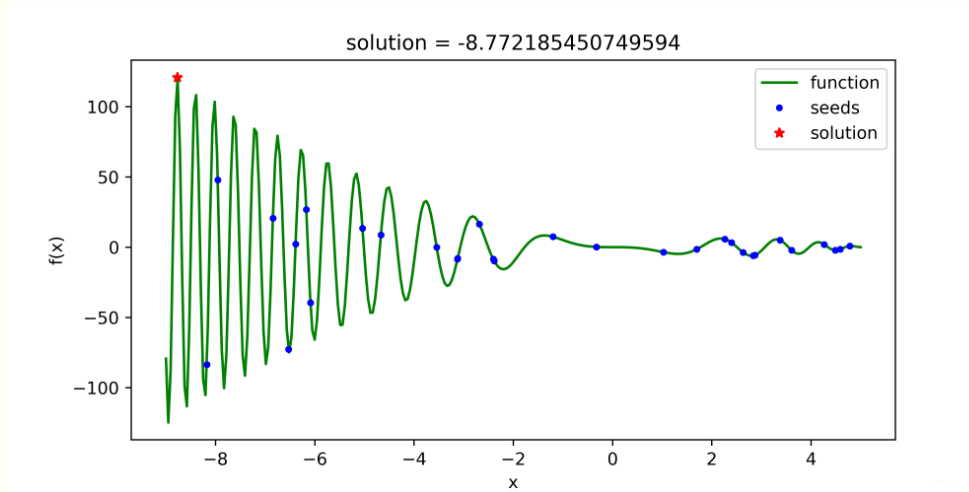
class parti(object):def __init__(self, v, x):self.v = v # 粒子当前速度self.x = x # 粒子当前位置self.pbest = x # 粒子历史最优位置class PSO(object):def __init__(self, interval, tab='min', partisNum=10, iterMax=1000, w=1, c1=2, c2=2):self.interval = interval # 给定状态空间 - 即待求解空间self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值self.iterMax = iterMax # 迭代求解次数self.w = w # 惯性因子self.c1, self.c2 = c1, c2 # 学习因子self.v_max = (interval[1] - interval[0]) * 0.1 # 设置最大迁移速度#####################################################################self.partis_list, self.gbest = self.initPartis(partisNum) # 完成粒子群的初始化,并提取群体历史最优位置self.x_seeds = np.array(list(parti_.x for parti_ in self.partis_list)) # 提取粒子群的种子状态 ###self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def initPartis(self, partisNum):partis_list = list()for i in range(partisNum):v_seed = random.uniform(-self.v_max, self.v_max)x_seed = random.uniform(*self.interval)partis_list.append(parti(v_seed, x_seed))temp = 'find_' + self.tabif hasattr(self, temp): # 采用反射方法提取对应的函数gbest = getattr(self, temp)(partis_list)else:exit('>>>tab标签传参有误:"min"|"max"<<<')return partis_list, gbestdef solve(self):for i in range(self.iterMax):for parti_c in self.partis_list:f1 = self.func(parti_c.x)# 更新粒子速度,并限制在最大迁移速度之内parti_c.v = self.w * parti_c.v + self.c1 * random.random() * (parti_c.pbest - parti_c.x) + self.c2 * random.random() * (self.gbest - parti_c.x)if parti_c.v > self.v_max: parti_c.v = self.v_maxelif parti_c.v < -self.v_max: parti_c.v = -self.v_max# 更新粒子位置,并限制在待解空间之内if self.interval[0] <= parti_c.x + parti_c.v <=self.interval[1]:parti_c.x = parti_c.x + parti_c.velse:parti_c.x = parti_c.x - parti_c.vf2 = self.func(parti_c.x)getattr(self, 'deal_'+self.tab)(f1, f2, parti_c) # 更新粒子历史最优位置与群体历史最优位置def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef find_min(self, partis_list): # 按状态函数最小值找到粒子群初始化的历史最优位置parti = min(partis_list, key=lambda parti: self.func(parti.pbest))return parti.pbestdef find_max(self, partis_list):parti = max(partis_list, key=lambda parti: self.func(parti.pbest)) # 按状态函数最大值找到粒子群初始化的历史最优位置return parti.pbestdef deal_min(self, f1, f2, parti_):if f2 < f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 < self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def deal_max(self, f1, f2, parti_):if f2 > f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 > self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def display(self):print('solution: {}'.format(self.gbest))plt.figure(figsize=(8, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seeds, self.func(self.x_seeds), 'b.', label='seeds')plt.plot(self.gbest, self.func(self.gbest), 'r*', label='solution')plt.xlabel('x')plt.ylabel('f(x)')plt.title('solution = {}'.format(self.gbest))plt.legend()plt.savefig('PSO.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':PSO([-9, 5], 'max')
效果
建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 案例:粒子群算法
文章目录 1 什么是粒子群算法?2 举个例子3 还是一个例子算法流程算法实现建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是粒子群算法? 粒子群算法(Pa…...

Tomcat 集群介绍
一.Tomcat 集群介绍 在实际生产环境中,单台 Tomcat 服务器的负载能力或者说并发能力在四五百左右。大 部分情况下随着业务增长,访问量的增加(并发量不止四五百),单台 Tomcat 服务器是 无法承受的。这时就需要将多台 Tomcat 服务器组织起来&a…...
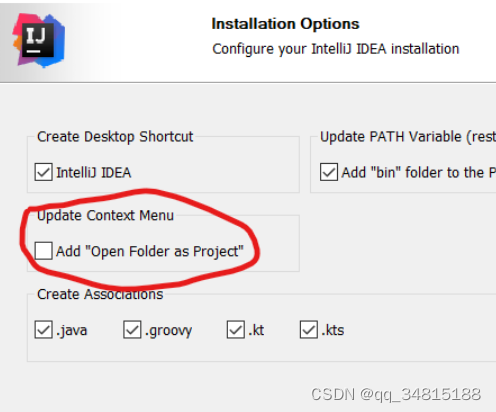
Windows右键添加用 IDEA 打开
1.安装IDEA时 安装时会有个选项来添加,如下: 勾选即可 2.修改注册表 安装时未勾选,可以把下面代码中程序路径改为自己的,保存为对应的 idea.reg文件,双击即可 Windows Registry Editor Version 5.00[HKEY_CLASSES…...

Golang 中return和defer执行先后顺序
先给出最终结论: 执行return语句 -> 执行defer函数 -> 函数返回 这里可能会有一个疑问, 执行return语句和函数返回难道不是一回事? Golang语言中函数的return不是原子操作,而是分为了两步: 返回值赋值真正函数返回 Gol…...

业务数据模拟/采集
业务数据模拟/采集 2.2 业务数据模拟 2.2.1 连接MySQL 通过MySQL可视化客户端连接数据库。2.2.2 建表语句 1)通过SQLyog创建数据库2)设置数据库名称为gmall,编码为utf-8,排序规则为utf8_general_ci3)导入数据库结构脚本…...
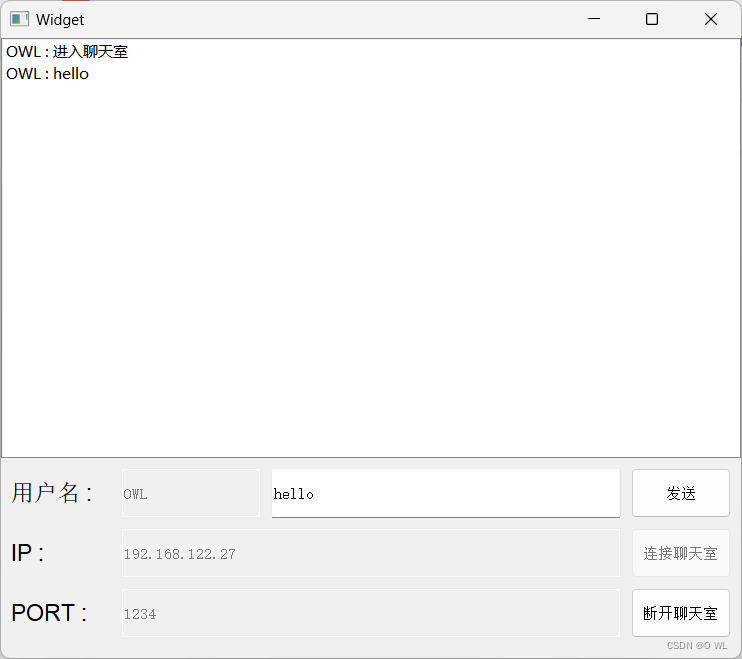
qt day 5
实现局域网的网络聊天室功能 1>服务器代码 --------------------------------------------------------------- widget.h --------------------------------------------------------------- #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMes…...

Java设计模式之适配器模式
适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁。这种类型的设计模式属于结构型模式,它结合了两个独立接口的功能。 这种模式涉及到一个单一的类,该类负责加入独立的或不兼容的接口功能。举个真实的例子࿰…...
2023.8.29 (DAP接口))
每天一个工业通信协议(3)2023.8.29 (DAP接口)
文章目录 参考文献1.DAP接口介绍2.DAP接口的2/3pin3.一种DAP接口方案应用的说明,通过两步初始化把JTAG接口变成DAP接口使用4.DAP接口的协议4.1 DAP电报的分类(只用JTAG类电报)4.2 电报格式4.3 DAP有限状态机参考文献 李婧. DAP模块验证组件系统级开发和实现[D]. 陕西:西安电…...
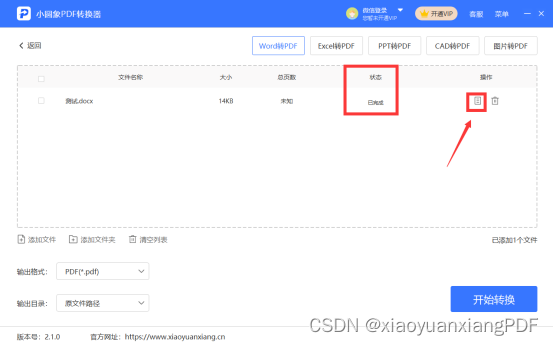
如何将Word转成PDF?试一下这个转换方法
Word转成PDF是现代办公中常见的需求,它可以确保文件的格式和内容在不同平台上保持一致,并且更加方便共享和打印。在这个数字化时代,我们经常需要将Word文档转换为PDF格式,无论是个人用户还是商务用户都会遇到这样的需求。那么如何…...

成都睿趣科技:现在开一家抖音小店还来得及吗
随着社交媒体的迅猛发展,抖音已经成为了一个全球范围内广受欢迎的社交平台。在这个短视频应用上,人们分享着各种各样的内容,从搞笑段子到美食教程,再到时尚搭配和手工艺品制作。随着用户数量的不断增长,很多人都在思考…...

原型链中:为什么Function.proto==Function.prototype?
背景: 在 JavaScript 中,每个函数(包括构造函数)都是一个对象,而对象都有一个 __proto__ 属性,指向它们的原型。当你创建一个函数时,JavaScript 引擎会自动为该函数创建一个原型对象,并将其关联…...

原生js实现轮播图及无缝滚动
我这里主要说轮播图和无缝滚动的实现思路,就采用最简单的轮播图了,当然实现的思路有很多种,我这也只是其中一种。 简单轮播图的大概结构是这样的,中间是图片,二边是箭头可以用来切换图片,下面的小圆点也可以…...
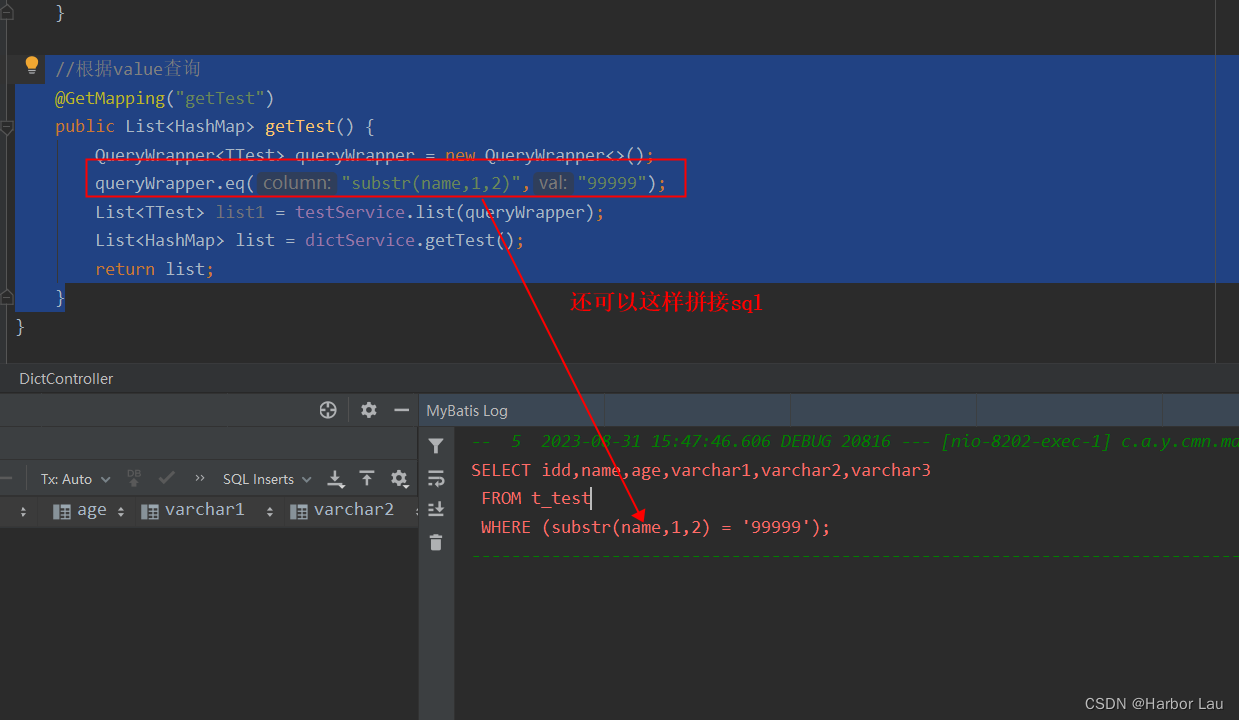
MP中的字段还可以利用函数来查询拼接sql
//根据value查询GetMapping("getTest")public List<HashMap> getTest() {QueryWrapper<TTest> queryWrapper new QueryWrapper<>();queryWrapper.eq("substr(name,1,2)","99999");List<TTest> list1 testService.list…...
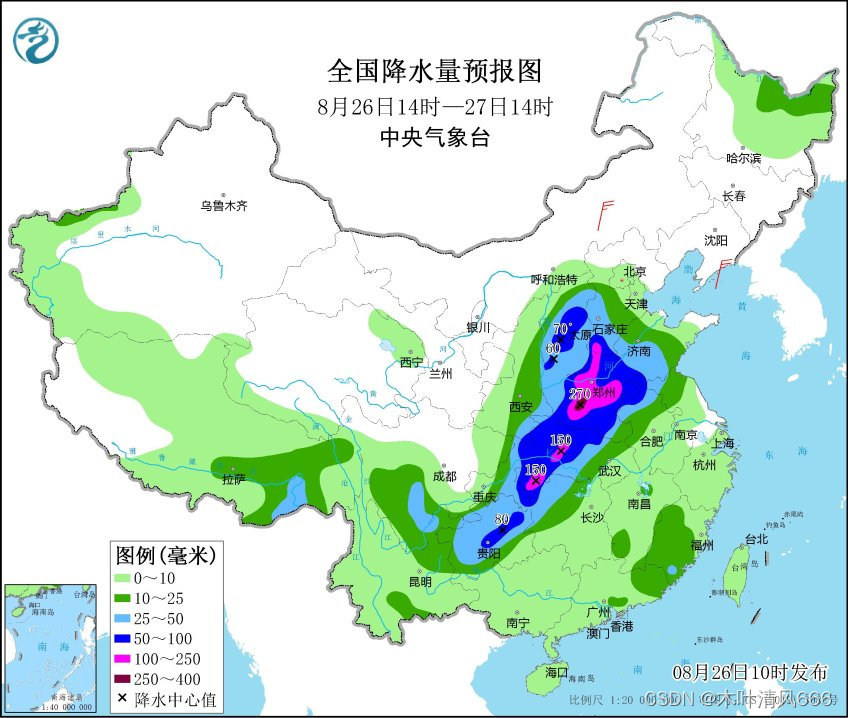
【python爬虫】中央气象局预报—静态网页图像爬取练习
静态网页爬取练习 中央气象局预报简介前期准备步骤Python爬取每日预报结果—以降水为例 中央气象局预报简介 中央气象台是中国气象局(中央气象台)发布的七天降水预报页面。这个页面提供了未来一周内各地区的降水预报情况,帮助人们了解即将到来…...

数字孪生城市总体架构进一步迭代更新
经过五年来发展,数字孪生城市基本形成“三横四纵”的总体架构,“三横”为新型基础设施、智能运行中枢、孪生应用体系,“四纵”为组织保障体系、标准规范体系、网络安全防线、运营保障体系,具体如下。 数字孪生城市总体架构-来源&a…...

通过 Jetbrains GateWay实现Remote Development
本次环境准备 环境准备:win10、一台安装有树莓派系统的树莓派(也可以是其他的服务器) 第一步:通过官网下载JetBrains Gateway 官网地址:https://www.jetbrains.com/remote-development/gateway/ 第二步:安装…...

springboot 集成 lucene
简介 数据每分钟产生200条,使用mysql储存。目前有数据超过700M。按照日期查询,按月查询包含每次超过20w条以上,时间比较长。计划使用lucene优化查询,不适用es是因为项目较小,没有更富裕的资源。 基本步骤 引入依赖。…...
Android开机动画
Android开机动画 1、BootLoader开机图片2、Kernel开机图片3、系统启动时(BootAnimation)动画3.1 bootanimation.zip位置3.2 bootanimation启动3.3 SurfaceFlinger启动bootanimation3.4 播放开机动画playAnimation3.6 开机动画退出检测3.7 简易时序图 4、…...

vue中使用wow.js
一、安装 npm install wowjs --save-dev 二、main中引入 animate.css会自动安装 因为wow.js在animate.css基础上 main.js中引入animate.css import "animate.css" 三、 页面使用 有两种引入使用方式:1. import {WOW} from wowjs mounted() { n…...
网站edge -- 油猴 -> IDM
一、百度网盘限速 未解决 软件:IDM 安装路径: 1.1如果:edge 出问题打不开其他网站, 解决方法: 以管理员的身份,右击载这个软件,就好了 1.2使用这个软件 应该是右击这个软件 以管理员的身…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
