算法通关村第十四关:黄金挑战-数据流的中位数
黄金挑战-数据流的中位数
1.数据流中中位数的问题
LeetCode295
https://leetcode.cn/problems/find-median-from-data-stream/
思路分析
中位数的问题,我们一般都可以用 大顶堆+小顶堆 来求解
小顶堆(minHeap):存储所有元素中较大的一半,堆顶元素是其中最小的数
大顶堆(maxHeap):存储所有元素中较小的一半,堆顶元素是其中最大的数
相当于,把所有元素分成了大和小两半,计算中位数,只需要大的那半的最小值和小的那半的最大值即可。
如[1,2,3,4,5],分成小顶堆[3,4,5],大顶堆[2,1],中位数为3
过程
加1 小顶堆[1] 大顶堆[] 中位数 1
加2 小顶堆[2] 大顶堆[1] 中位数 (2+1)/2
加3 小顶堆[2,3] 大顶堆[1] 中位数 3
加4 小顶堆[3,4] 大顶堆[2,1] 中位数 (3+2)/2
加5 小顶堆[3,4,5] 大顶堆[2,1] 中位数 3
代码实现
Java中的堆(即优先队列)可方便实现,c++、python里没有提供堆结构,需要自己构造
class MedianFinder {// 小顶堆中存储的是比较大的元素,堆顶是其中的最小值PriorityQueue<Integer> minHeap;// 大顶堆中存储的是比较小的元素,堆顶是中期的最大值PriorityQueue<Integer> maxHeap;public MedianFinder() {this.minHeap = new PriorityQueue<>();this.maxHeap = new PriorityQueue<>((a, b) -> b - a);}public void addNum(int num) {// 小顶堆存储的是比较大的元素,num大于小顶堆中根元素时进入minHeapif (minHeap.isEmpty() || num > minHeap.peek()){minHeap.offer(num);// 如果minHeap比maxHeap多2个元素,就平衡一下if (minHeap.size() - maxHeap.size() > 1){maxHeap.offer(minHeap.poll());}}else{maxHeap.offer(num);// 这样可以保证多的那个元素肯定在minHeapif(maxHeap.size() - minHeap.size() > 0){minHeap.offer(maxHeap.poll());}}}public double findMedian() {if(minHeap.size() > maxHeap.size()){return minHeap.peek();}else if(minHeap.size() < maxHeap.size()){return maxHeap.peek();}else{return (minHeap.peek() + maxHeap.peek())/2.0;}}
}/*** Your MedianFinder object will be instantiated and called as such:* MedianFinder obj = new MedianFinder();* obj.addNum(num);* double param_2 = obj.findMedian();*/
相关文章:

算法通关村第十四关:黄金挑战-数据流的中位数
黄金挑战-数据流的中位数 1.数据流中中位数的问题 LeetCode295 https://leetcode.cn/problems/find-median-from-data-stream/ 思路分析 中位数的问题,我们一般都可以用 大顶堆小顶堆 来求解 小顶堆(minHeap):存储所有元素中…...
【2023集创赛】国家集创中心杯三等奖:不对称轻失配运算放大器
本文为2023年第七届全国大学生集成电路创新创业大赛(“集创赛”)国家集创中心杯三等奖作品分享,参加极术社区的【有奖征集】分享你的2023集创赛作品,秀出作品风采,分享2023集创赛作品扩大影响力,更有丰富电…...

手写Mybatis:第18章-一级缓存
文章目录 一、目标:一级缓存二、设计:一级缓存三、实现:一级缓存3.1 工程结构3.2 一级缓存类图3.3 一级缓存实现3.3.1 定义缓存接口3.3.2 实现缓存接口3.3.3 创建缓存KEY3.3.4 NULL值缓存key 3.4 定义缓存机制、占位符和修改配置文件3.4.1 定…...

哈夫曼编码实现文件的压缩和解压
程序示例精选 哈夫曼编码实现文件的压缩和解压 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《哈夫曼编码实现文件的压缩和解压》编写代码,代码整洁,规则࿰…...

解决六大痛点促进企业更好使用生成式AI,亚马逊云科技顾凡采访分享可用方案
亚马逊云科技大中华区战略业务发展部总经理顾凡在接受21世纪经济报道记者专访时表示,生成式人工智能将从四个方面为企业带来机遇:第一是创造全新的客户体验;第二是提高企业内部员工的生产力;第三是帮助企业提升业务运营效率&#…...

Qt 定时器放在线程中执行,支持随时开始和停止定时器。
前言:因为项目需要定时检查网络中设备是否能连通,需要定时去做ping操作,若是网络不通,则ping花费时间比较久(局域网大概4秒钟才能结束,当然如果设置超时时间啥的,也能很快返回,就是会…...
验证入参,验签(sign) Demo)
java 过滤器 接口(API)验证入参,验签(sign) Demo
java 过滤器 接口(API)验证入参,验签(sign) Demo 一、思路 1、配置yml文件; 2、创建加载配置文件类; 3、继承 OncePerRequestFilter 重写方法 doFilterInternal; 4、注册自定义过滤器; 二、步骤 1、配置yml文件; ###系…...

独家!微信正在灰测一款全新消金产品
来源 | 镭射财经(leishecaijing) 「镭射财经」独家获悉,微信将推出一款名为“微信分期”的新消费信贷产品,目前该产品正处于小范围灰测阶段,还未正式上线。上线后,微信将运营微信分付和微信分期两款自营消…...

阿秀C++笔记-学习记录
81.C中的组合和继承相比的优缺点 在C中组合一对象系用描述对象包对象系组一个拥对象例其变合类的含的现。这的量类当有员被创建。 以下一个示例,展示了在C中如何实现组合关系: class Engine {// Engine class definition... };class Car {Engine engi…...

前端入门到入土?
文章目录 前言http和https的区别,https加密的原理是?区别https的加密原理 TCP为什么要三次握手?proxy代理的原理?内存泄漏?什么是内存泄漏?为什么会有内存泄漏?内存泄漏的情况?如何防…...
架构设计基础设施保障IaaS之网络
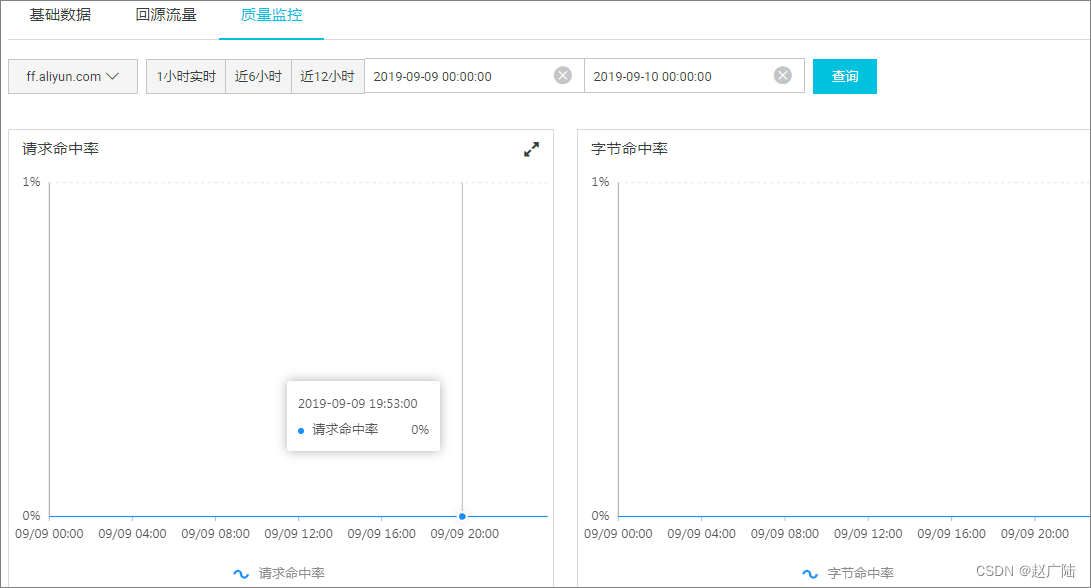
目录 1 DNS运用1.1 DNS功能作用1.2 DNS配置实践 2 DNS生产最佳实践方案2.1 全球加速功能2.2 不同运营商的加速方案2.3 全球业务高可用方案2.4 跨地域负载均衡 3 DNS域名劫持解决方案4 CDN剖析4.1 CDN原理4.2 缓存过期配置处理流程4.3 缓存配置规则 5 CDN运用6 CDN最佳实践方案6…...
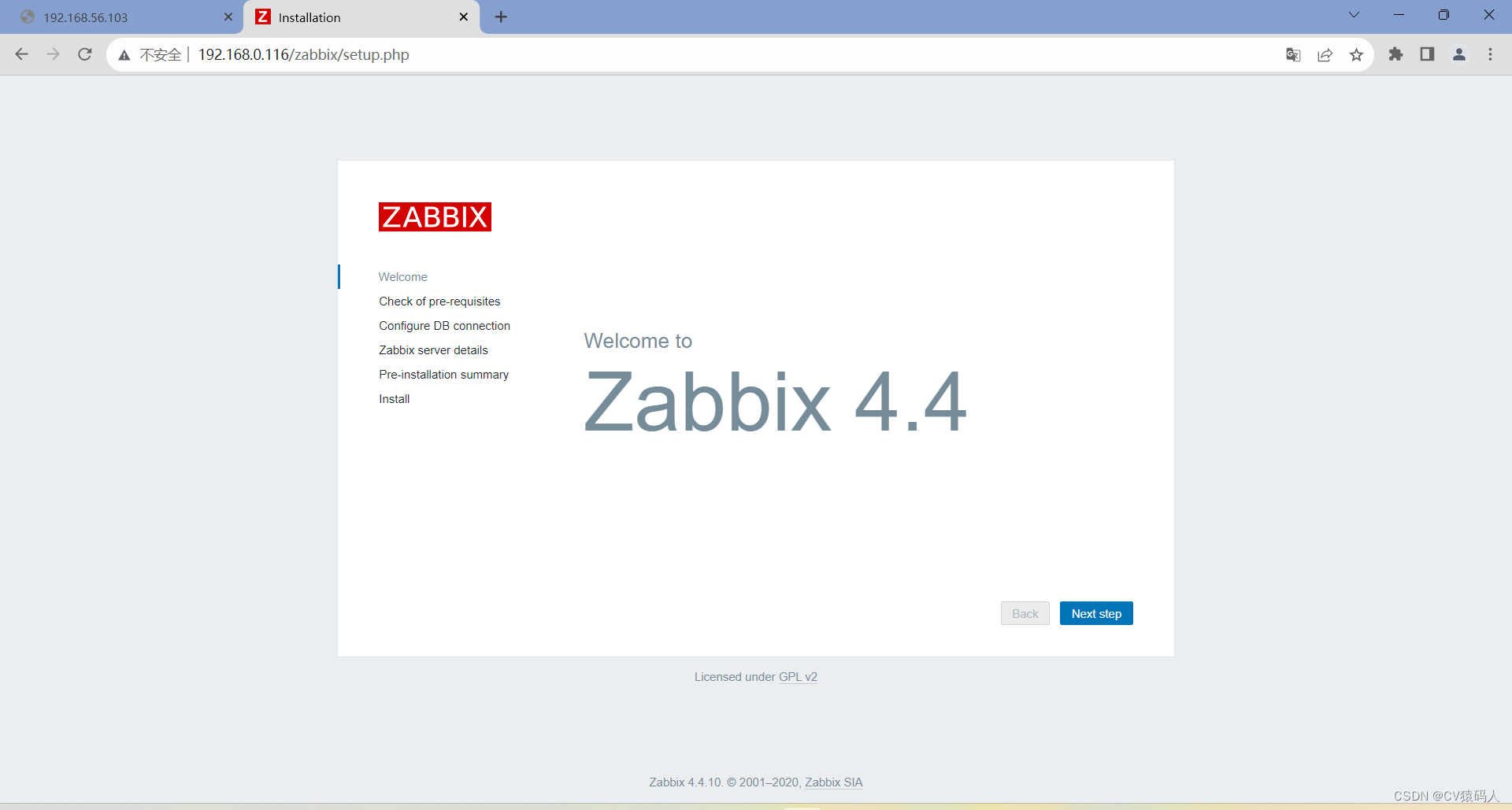
zabbix安装部署
前期准备:安装mysql数据库和nginx 一、下载zabbix rpm -Uvh https://repo.zabbix.com/zabbix/4.4/rhel/7/x86_64/zabbix-release-4.4-1.el7.noarch.rpm yum-config-manager --enable rhel-7-server-optional-rpms yum install epel-release numactl yum install…...

零碎的C++
构造函数和析构函数 构造函数不能是虚函数,而析构函数可以是虚函数。原因如下: 构造函数不能是虚函数,因为在执行构造函数时,对象还没有完全创建,还没有分配内存空间,也没有初始化虚函数表指针。如果构造…...
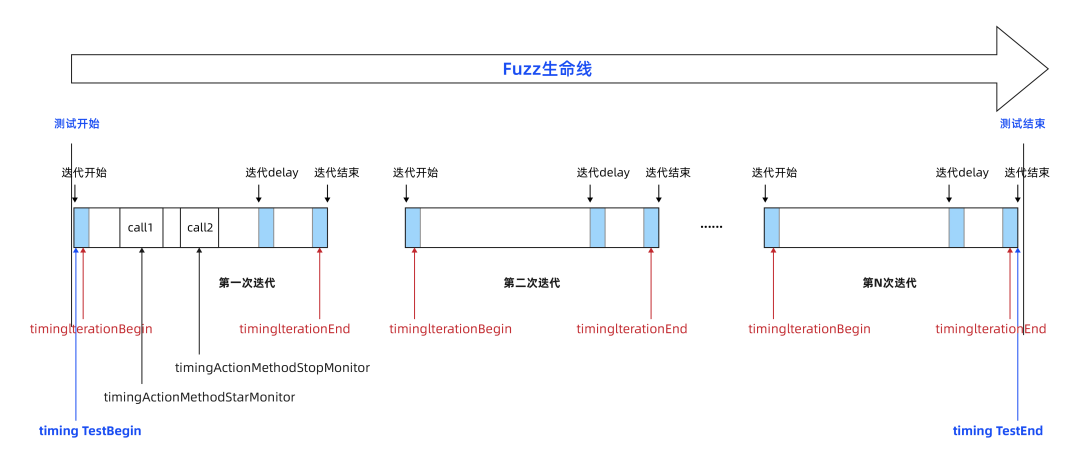
模糊测试面面观 | 模糊测试是如何发现异常情况的?
协议模糊测试是一种用于评估通信协议、文件格式和API实现系统安全性和稳定性的关键技术。在模糊测试过程中,监视器扮演着关键角色,它们能够捕获异常情况、错误响应、资源利用等,为测试人员提供有价值的信息,有助于发现潜在漏洞和问…...
C#备份数据库文件
c#备份数据库文件完整代码 sqlServer 存储过程: USE [PSIDBase] GO /****** Object: StoredProcedure [dbo].[sp_BackupDB] Script Date: 2023/8/31 16:49:02 ******/ SET ANSI_NULLS ON GO SET QUOTED_IDENTIFIER ON GOALTER procedure [dbo].[sp_BackupDB]…...

行军遇到各种复杂地形怎么处理?
行军遇到各种复杂地形怎么处理? 【安志强趣讲《孙子兵法》第30讲】 【原文】 凡军好高而恶下,贵阳而贱阴,养生而处实,军无百疾,是谓必胜。 【注释】 阳,太阳能照到的地方。阴,太阳照不到的地方。…...
.............................................)
Python Number(数字).............................................
Python Number 数据类型用于存储数值。 数据类型是不允许改变的,这就意味着如果改变 Number 数据类型的值,将重新分配内存空间。 以下实例在变量赋值时 Number 对象将被创建: var1 1 var2 10您也可以使用del语句删除一些 Number 对象引用。 del语句…...

设置 Hue Server 与 Hue Web 界面之间的会话超时时间
设置 Hue Server 与 Hue Web 界面之间的会话超时时间 在 CDH 的 Hue 中,Auto Logout Timeout 参数表示用户在不活动一段时间后将自动注销(登出)的超时时间。当用户在 Hue 中处于不活动状态超过该设定时间时,系统将自动注销用户&am…...

openGauss学习笔记-57 openGauss 高级特性-并行查询
文章目录 openGauss学习笔记-57 openGauss 高级特性-并行查询57.1 适用场景与限制57.2 资源对SMP性能的影响57.3 其他因素对SMP性能的影响57.4 配置步骤 openGauss学习笔记-57 openGauss 高级特性-并行查询 openGauss的SMP并行技术是一种利用计算机多核CPU架构来实现多线程并行…...
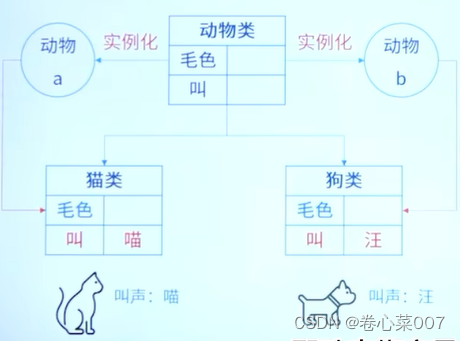
软考(1)-面向对象的概念
目录 一. 软考基本信息 1. 软考时间: 2. 软考科目: 3.专业知识介绍 -- 综合知识考点分布 4. 专业介绍 -- 软件设计考点分布 二. 面向对象概念 1. 封装 考点一:对象 考点二:封装private 2. 继承 考点三:类 考…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
