机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质
- 引言
- 凸函数的定义
- 严格凸函数
- 凸函数的推论:凹函数
- 常见凸函数
- 凸函数的基本性质
- 几种保持函数凸性的运算
- 凸集与凸函数之间的关联关系
引言
本节将介绍凸函数定义及其基本性质。
本文是关于梯度下降法:凸函数 VS \text{VS} VS强凸函数的逻辑补充。涉及的证明过程如:
- 凸函数的一阶条件;
- 凸函数的梯度单调性;
- 凸函数的二阶条件
详见上述链接。
凸函数的定义
关于凸函数的基本定义表示如下:
假设 C \mathcal C C是非空凸集, f ( ⋅ ) f(\cdot) f(⋅)是定义在 C \mathcal C C上的函数,如果对于 ∀ x , y ∈ C \forall x,y \in \mathcal C ∀x,y∈C且 α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1),均有:
关于凸集的概念、基本性质、凸组合详见凸集的简单认识。
f [ α ⋅ x + ( 1 − α ) ⋅ y ] ≤ α ⋅ f ( x ) + ( 1 − α ) ⋅ f ( y ) f[\alpha \cdot x + (1 - \alpha) \cdot y] \leq \alpha \cdot f(x) + (1 - \alpha) \cdot f(y) f[α⋅x+(1−α)⋅y]≤α⋅f(x)+(1−α)⋅f(y)
则称函数 f ( ⋅ ) f(\cdot) f(⋅)为凸集 C \mathcal C C上的凸函数。
- 观察不等式左侧:其中 α ⋅ x + ( 1 − α ) ⋅ y \alpha \cdot x + (1 - \alpha) \cdot y α⋅x+(1−α)⋅y是点 x , y x,y x,y的凸组合,也就是连接点 x , y x,y x,y的线段上的点;而 f [ α ⋅ x + ( 1 − α ) ⋅ y ] f[\alpha \cdot x + (1 - \alpha) \cdot y] f[α⋅x+(1−α)⋅y]则表示连接点 x , y x,y x,y线段上点的函数值。
- 观察不等式右侧:同左侧,它描述的是:点 f ( x ) , f ( y ) f(x),f(y) f(x),f(y)的凸组合,并始终满足小于等于的关系。
凸函数的几何意义解释如下图所示:
很明显,橙色点相比于黄色点对应的函数值要小。当x , y x,y x,y两点重合时,上式取等。

相反,某函数的函数图像表示如下:
在x , y x,y x,y这种取值的情况下,并不满足上述函数。因而该函数不是一个凸函数。

严格凸函数
严格凸函数是在凸函数的基础上增加了相关要求。它的定义方式仅将凸函数的定义修改为:
从而对 x , y ∈ C x,y \in \mathcal C x,y∈C条件下增加了新的要求:点 x , y x,y x,y不能重合。
f [ α ⋅ x + ( 1 − α ) ⋅ y ] < α ⋅ f ( x ) + ( 1 − α ) ⋅ f ( y ) f[\alpha \cdot x + (1 - \alpha) \cdot y] < \alpha \cdot f(x) + (1 - \alpha) \cdot f(y) f[α⋅x+(1−α)⋅y]<α⋅f(x)+(1−α)⋅f(y)
很明显,上面描述的第一个图像对应的函数是严格凸函数;相反:什么样的函数是凸函数,但不是严格凸函数 ? ? ?例如线性函数 f ( x ) = x f(x) = x f(x)=x,它的函数图像就是一条直线:

上述函数完全满足凸函数的定义;但不满足严格凸函数的定义。
凸函数的推论:凹函数
如果从定义的角度表述,那么凹函数的定义方式仅将凸函数的定义修改为:
其他条件不变~
f [ α ⋅ x + ( 1 − α ) ⋅ y ] ≥ α ⋅ f ( x ) + ( 1 − α ) ⋅ f ( y ) f[\alpha \cdot x + (1 - \alpha) \cdot y] \geq \alpha \cdot f(x) + (1 - \alpha) \cdot f(y) f[α⋅x+(1−α)⋅y]≥α⋅f(x)+(1−α)⋅f(y)
同上,凹函数的函数图像示例如下:

从凸函数的角度观察,可以得到推论:若 − f ( ⋅ ) -f(\cdot) −f(⋅)是凸函数,则 f ( ⋅ ) f(\cdot) f(⋅)是凹函数。
延伸:如果是关于凹函数 f ( x ) f(x) f(x)的优化问题,如 max f ( x ) \max f(x) maxf(x);可以将其转化为相应凸函数的优化问题: min − f ( x ) \min -f(x) min−f(x)。
常见凸函数
常见凸函数有如下几种:
- 线性函数: f ( x ) = A T x + b f(x) = \mathcal A^T x + b f(x)=ATx+b;需要注意的是:线性函数是唯一一类既是凸函数,也是凹函数的函数。
- 二次函数:它由二次型 x T Q x x^T\mathcal Q x xTQx与线性函数 A T x + b \mathcal A^Tx + b ATx+b组成:
f ( x ) = x T Q x + A T x + b f(x) = x^T \mathcal Q x + \mathcal A^Tx + b f(x)=xTQx+ATx+b
其中 Q ∈ S + n \mathcal Q \in \mathcal S_{+}^n Q∈S+n。在凸集的简单认识(上)中介绍过, S + n \mathcal S_{+}^n S+n描述的可行域是半定矩阵锥:所有 n n n阶半正定矩阵组成的集合:
其中集合S n \mathcal S^n Sn描述所有 n n n阶对称矩阵组成的集合。
S + n { X ∈ S n ∣ X ≽ 0 } \mathcal S_{+}^n \{\mathcal X \in \mathcal S^n \mid \mathcal X \succcurlyeq 0\} S+n{X∈Sn∣X≽0}
并且 S + n \mathcal S_{+}^n S+n是一个凸集;也就是说:矩阵 Q \mathcal Q Q必然至少是一个半正定矩阵。相反,如果对称矩阵 Q \mathcal Q Q的特征值存在负值(如不定矩阵)甚至是负定矩阵,那么对应二次型 x T Q x x^T \mathcal Qx xTQx展开后其二次项系数可能是负值,对应的二次函数就不是凸函数。 - 最小二乘函数:在线性回归一节中介绍了最小二乘法 ( Least Square Method ) (\text{Least Square Method}) (Least Square Method):它通常在线性回归任务中描述模型预测结果与真实标签之间差异性的考量:
L ( W ) = ∑ i = 1 N ∥ W T x ( i ) − y ( i ) ∥ 2 2 \mathcal L(\mathcal W) = \sum_{i=1}^N \|\mathcal W^T x^{(i)} - y^{(i)}\|_2^2 L(W)=i=1∑N∥WTx(i)−y(i)∥22
其中 ( x ( i ) , y ( i ) ) ∈ D = { ( x ( i ) , y ( i ) ) } i = 1 N (x^{(i)},y^{(i)}) \in \mathcal D = \{(x^{(i)},y^{(i)})\}_{i=1}^N (x(i),y(i))∈D={(x(i),y(i))}i=1N。而最小二乘函数定义为如下形式:
f ( x ) = ∥ A x − b ∥ 2 2 f(x) = \|\mathcal Ax - b\|_2^2 f(x)=∥Ax−b∥22
实际上,该函数可将其描述为二次函数:
f ( x ) = ∥ A x − b ∥ 2 2 = ( A x − b ) T ( A x − b ) = ( A x ) T A x − b T A x − ( A x ) T b + b T b = x T A T A x + b T A x − x T A T b + b T b \begin{aligned} f(x) & = \|\mathcal A x - b\|_2^2 \\ & = (\mathcal Ax - b)^T (\mathcal A x - b) \\ & = (\mathcal Ax)^T \mathcal Ax - b^T\mathcal Ax - (\mathcal Ax)^T b + b^Tb \\ & = x^T \mathcal A^T \mathcal A x + b^T \mathcal Ax - x^T \mathcal A^T b + b^T b \\ \end{aligned} f(x)=∥Ax−b∥22=(Ax−b)T(Ax−b)=(Ax)TAx−bTAx−(Ax)Tb+bTb=xTATAx+bTAx−xTATb+bTb
很明显,对应上式中的二次型是: x T A T A x x^T \mathcal A^T \mathcal A x xTATAx,而矩阵 A T A \mathcal A^T \mathcal A ATA必然至少是一个半正定矩阵。因此:最小二乘函数一定是凸函数。 - m m m范数函数:在正则化——拉格朗日乘数法角度中介绍过明可夫斯基距离 ( Minikowski Distance ) (\text{Minikowski Distance}) (Minikowski Distance)。关于向量 x ( i ) ∈ R p x^{(i)} \in \mathbb R^p x(i)∈Rp与 p p p维空间原点之间的明可夫斯基距离表示如下:
∥ x ( i ) ∥ p = [ ∑ k = 1 p ∣ x k ( i ) − 0 ∣ m ] 1 m \|x^{(i)}\|_p = \left[\sum_{k=1}^p |x_k^{(i)} - 0|^m\right]^{\frac{1}{m}} ∥x(i)∥p=[k=1∑p∣xk(i)−0∣m]m1
可以将上述函数描述为关于向量 x ( i ) x^{(i)} x(i)的函数 f [ x ( i ) ] f[x^{(i)}] f[x(i)]:
f ( x ) = [ ∑ k = 1 p ∣ x k ∣ m ] 1 m f(x) = \left[\sum_{k=1}^p |x_k|^m\right]^{\frac{1}{m}} f(x)=[k=1∑p∣xk∣m]m1
其中关于 m ≥ 0 m \geq 0 m≥0时,函数 f ( x ) f(x) f(x)在 m m m不同取值的函数图像示例表示如下:
其中当m = 0 m=0 m=0时,f ( x ) = ∥ x ∥ 0 f(x) = \|x\|_0 f(x)=∥x∥0即x x x非零分量的个数。它是一个非凸函数~

根据凸函数定义可以看出:当 m ≥ 1 m \geq 1 m≥1时,该函数是凸函数;该函数围城的区域是凸集。因而,在 m ≥ 1 m \geq 1 m≥1时, m m m范函数才是凸函数。
凸函数的基本性质
-
如果 f ( x ) f(x) f(x)是凸函数,那么 f ( x ) f(x) f(x)自身在其定义域内一定是连续函数。
-
如果 f ( x ) f(x) f(x)是凸函数 ⇔ ∀ x , y ∈ R n \Leftrightarrow \forall x,y \in \mathbb R^n ⇔∀x,y∈Rn,一元函数 ϕ ( α ) \phi(\alpha) ϕ(α)表示如下:
ϕ ( α ) = f ( x + α ⋅ y ) \phi(\alpha) = f(x + \alpha \cdot y) ϕ(α)=f(x+α⋅y)
并且该函数是凸函数。如果从几何意义的角度解释:由于向量 x , y x,y x,y已知,那么向量 x + α ⋅ y x + \alpha \cdot y x+α⋅y可看作是:从向量 x x x所在位置出发,沿着向量 y y y的方向,移动一段距离后的向量结果。只不过这个距离由 α \alpha α控制。对应图像表示如下:
如果α \alpha α是负值,相当于沿着向量 y y y的反方向移动相应的距离。下图中的y y y更多表示移动的方向;而α ∈ R \alpha \in \mathbb R α∈R控制移动的距离。
那么关于 ϕ ( α ) = f ( x + α ⋅ y ) \phi(\alpha) = f(x + \alpha \cdot y) ϕ(α)=f(x+α⋅y)它的函数图像示例如下:
其中黄色平面描述 x + α ⋅ y x + \alpha \cdot y x+α⋅y的函数图像,而f ( x + α ⋅ y ) f(x + \alpha \cdot y) f(x+α⋅y)则表示x + α ⋅ y x+\alpha \cdot y x+α⋅y的函数图像与凸函数 f ( ⋅ ) f(\cdot) f(⋅)对应函数图像切面产生的图像黄色虚线,可以看出,这个切面图像也是一个凸函数。

-
凸函数的一阶条件: f ( x ) f(x) f(x)是 C \mathcal C C上的凸函数充要条件是:
f ( y ) ≥ f ( x ) + [ ∇ f ( x ) ] T ( y − x ) ∀ x , y ∈ C f(y) \geq f(x) + [\nabla f(x)]^T (y - x) \quad \forall x,y \in \mathcal C f(y)≥f(x)+[∇f(x)]T(y−x)∀x,y∈C
该条件的几何图像描述表示如下:
假设将x x x固定住,此时∇ f ( x ) \nabla f(x) ∇f(x)是一个常量,它表示函数 f ( ⋅ ) f(\cdot) f(⋅)在 x x x点处的斜率从而不等式右侧是关于y y y的一次函数,并且经过点 [ x , f ( x ) ] [x,f(x)] [x,f(x)]。可以发现:f ( y ) f(y) f(y)的图像总是在 ϕ ( y ) \phi(y) ϕ(y)的上方(可以重合)。

相反,非凸函数并不具备这个性质。示例如下:
此时f ( y ) < ϕ ( y ) f(y) < \phi(y) f(y)<ϕ(y)。

其证明过程见开头链接,这里不再赘述。 -
凸函数的二阶条件:假设 C ⊂ R n \mathcal C \sub \mathbb R^n C⊂Rn是非空开凸集,并且函数 f ( x ) f(x) f(x)在 C \mathcal C C上二阶连续可微,则有:
f ( x ) is Convex ⇔ ∇ 2 f ( x ) ≽ 0 , ∀ x ∈ C f(x)\text{ is Convex } \Leftrightarrow \nabla^2 f(x) \succcurlyeq 0, \forall x \in \mathcal C f(x) is Convex ⇔∇2f(x)≽0,∀x∈C
如果 x x x是一个标量,那么它关于函数 f ( ⋅ ) f(\cdot) f(⋅)在 x x x点处的 Hessian Matrix ⇒ ∇ 2 f ( x ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x) Hessian Matrix⇒∇2f(x)则退化成二阶导数 f ′ ′ ( x ) f''(x) f′′(x)。这意味着: f ′ ′ ( x ) ≥ 0 ⇒ f ′ ( x ) f''(x) \geq 0 \Rightarrow f'(x) f′′(x)≥0⇒f′(x)的变化率随着 x x x的增加,处于一个增加/稳定的状态。同上,这里的证明见开头链接,这里不再赘述。
几种保持函数凸性的运算
在函数 f ( x ) f(x) f(x)是凸函数的基础上,对 f ( x ) f(x) f(x)执行一些运算/变换,运算结果其凸函数性质保持不变。
- 透视函数 ( Perspective Function ) (\text{Perspective Function}) (Perspective Function):若 f ( x ) f(x) f(x)是凸函数, x ∈ R n x \in \mathbb R^n x∈Rn。令:
此时G ( ⋅ ) \mathcal G(\cdot) G(⋅)函数内的变量有n + 1 n+1 n+1个。
G ( x , t ) = t ⋅ f ( x t ) t > 0 \mathcal G(x,t) = t \cdot f \left(\frac{x}{t} \right) \quad t > 0 G(x,t)=t⋅f(tx)t>0
则 G ( x , t ) \mathcal G(x,t) G(x,t)也是凸函数。
这里假设 f ( x ) f(x) f(x)是一元函数,且 f ( x ) = x 2 f(x) = x^2 f(x)=x2,那么对应的 G ( x , t ) = x 2 t \begin{aligned}\mathcal G(x,t) = \frac{x^2}{t}\end{aligned} G(x,t)=tx2。该二元函数对应的函数图像表示如下:
即虚线描述的范围,如一个展开的光幕~凑合看吧。其中[ 0 , 1 ] [0,1] [0,1]的部分这里没有表示~

- 非负组合:若 f i ( x ) ( i = 1 , 2 , ⋯ , m ) f_i(x)(i=1,2,\cdots,m) fi(x)(i=1,2,⋯,m)均是凸函数,对于 W i ≥ 0 ( i = 1 , 2 , ⋯ , m ) \mathcal W_i \geq 0(i=1,2,\cdots,m) Wi≥0(i=1,2,⋯,m),有:
G ( x ) = ∑ i = 1 m W i ⋅ f i ( x ) \mathcal G(x) = \sum_{i=1}^m \mathcal W_i \cdot f_i(x) G(x)=i=1∑mWi⋅fi(x)
那么 G ( x ) \mathcal G(x) G(x)是凸函数。
可以观察 G ( x ) \mathcal G(x) G(x)函数在 x x x点处的 Hessian Matrix ⇒ ∇ 2 G ( x ) \text{Hessian Matrix} \Rightarrow \nabla^2 \mathcal G(x) Hessian Matrix⇒∇2G(x):
∇ 2 G ( x ) = ∑ i = 1 m W i ⋅ ∇ 2 f i ( x ) \nabla^2 \mathcal G(x) = \sum_{i=1}^m \mathcal W_i \cdot \nabla^2 f_i(x) ∇2G(x)=i=1∑mWi⋅∇2fi(x)
很明显, ∇ 2 f i ( x ) ( i = 1 , 2 , ⋯ , m ) \nabla^2 f_i(x)(i=1,2,\cdots,m) ∇2fi(x)(i=1,2,⋯,m)必然是半正定的;各 ∇ 2 f i ( x ) \nabla^2 f_i(x) ∇2fi(x)对应的线性组合 ( W i ≥ 0 ) (\mathcal W_i \geq 0) (Wi≥0),其最终结果必然也是半正定的。 - 一组凸函数求最大值:已知 f i ( x ) ( i = 1 , 2 , ⋯ , m ) f_i(x)(i=1,2,\cdots,m) fi(x)(i=1,2,⋯,m)是凸函数,有:
G ( x ) = max { f i ( x ) } i = 1 , 2 , ⋯ , m \mathcal G(x) = \max \{f_i(x)\} \quad i=1,2,\cdots,m G(x)=max{fi(x)}i=1,2,⋯,m
那么 G ( x ) \mathcal G(x) G(x)是凸函数。示例图像表示如下:
求最大值实际上是求交集的一种情况。

凸集与凸函数之间的关联关系
-
工具 1 1 1 - 水平集。其定义对应数学符号描述表示如下:
L a = { x ∣ f ( x ) ≤ a , x ∈ C } \mathcal L_a = \{x \mid f(x) \leq a,x \in \mathcal C\} La={x∣f(x)≤a,x∈C}
任意函数都可以定义水平集,其中 a a a被称作水平值。以二元凸函数为例,给定水平集 a a a,相当于水平集所描述平面横截二元函数图像,并将处在水平集下方的函数图像进行投影。对应图像表示如下:

可以明显观察到:投影产生的集合明显是一个凸集。可以使用凸集定义进行证明:- 假设 f ( ⋅ ) f(\cdot) f(⋅)是凸函数,存在值 a a a,其水平集表示为 L a \mathcal L_a La。
- ∀ x , y ∈ L a ; ∀ λ ∈ [ 0 , 1 ] \forall x,y \in \mathcal L_a;\forall \lambda \in [0,1] ∀x,y∈La;∀λ∈[0,1],仅需要判断: λ ⋅ x + ( 1 − λ ) ⋅ y \lambda \cdot x + (1 - \lambda) \cdot y λ⋅x+(1−λ)⋅y是否也在 L a \mathcal L_a La内即可。观察 f [ λ ⋅ x + ( 1 − λ ) ⋅ y ] f[\lambda \cdot x + (1 - \lambda) \cdot y] f[λ⋅x+(1−λ)⋅y]的结果:
f [ λ ⋅ x + ( 1 − λ ) ⋅ y ] ≤ λ ⋅ f ( x ) + ( 1 − λ ) ⋅ f ( y ) f[\lambda \cdot x + (1 - \lambda) \cdot y] \leq \lambda \cdot f(x) + (1 - \lambda) \cdot f(y) f[λ⋅x+(1−λ)⋅y]≤λ⋅f(x)+(1−λ)⋅f(y)
由于 f ( x ) ≤ a f(x) \leq a f(x)≤a且 f ( y ) ≤ a f(y) \leq a f(y)≤a因而 λ ⋅ f ( x ) + ( 1 − λ ) ⋅ f ( y ) ≤ a \lambda \cdot f(x) + (1 - \lambda) \cdot f(y) \leq a λ⋅f(x)+(1−λ)⋅f(y)≤a恒成立。从而 λ ⋅ x + ( 1 − λ ) ⋅ y \lambda \cdot x + (1 - \lambda) \cdot y λ⋅x+(1−λ)⋅y也在 L a \mathcal L_a La内。因而 L a \mathcal L_a La必然是一个凸集。
\quad
相反呢 ? ? ?如果任意取 a a a,函数 f ( x ) f(x) f(x)对应的水平集均是凸集,那么 f ( ⋅ ) f(\cdot) f(⋅)是否为凸函数 ? ? ?不一定。如下图描述的函数:

-
工具 2 2 2 - EpiGragh \text{EpiGragh} EpiGragh。关于函数 f ( x ) f(x) f(x)的 EpiGragh \text{EpiGragh} EpiGragh定义表示如下:
Epi ( f ) = { ( x y ) ∣ f ( x ) ≤ y , x ∈ C } \text{Epi}(f) = \left\{\begin{pmatrix}x \\ y\end{pmatrix} \mid f(x) \leq y,x \in \mathcal C \right\} Epi(f)={(xy)∣f(x)≤y,x∈C}
其中 y y y是一个变量,仅满足: f ( x ) ≤ y f(x) \leq y f(x)≤y即可。很明显,若 x ∈ R n x \in \mathbb R^n x∈Rn,那么 ( x y ) \begin{pmatrix}x \\ y\end{pmatrix} (xy)是一个 n + 1 n+1 n+1维向量。而 Epi(f) \text{Epi(f)} Epi(f)就是由该向量组成的集合。如果 f ( x ) f(x) f(x)是一个一维函数,那么它对应的 EpiGragh \text{EpiGragh} EpiGragh示例如下:
由于y y y进满足f ( x ) ≤ y f(x) \leq y f(x)≤y即可,因此阴影部分可以无限向上延伸( y ⇒ ∞ ) (y \Rightarrow \infty) (y⇒∞),这里没有画出来。

其中阴影部分即 Epi(f) \text{Epi(f)} Epi(f)描述的集合。很明显,它比 x x x要高一维。关于 EpiGraph \text{EpiGraph} EpiGraph的一个充要条件:
f ( ⋅ ) is Convex Function ⇔ Epi ( f ) is Convex Set f(\cdot) \text{ is Convex Function} \Leftrightarrow \text{Epi}(f) \text{ is Convex Set} f(⋅) is Convex Function⇔Epi(f) is Convex Set
Reference \text{Reference} Reference:
最优化理论与方法-第三讲-凸函数:定义与基本性质
相关文章:

机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质 引言凸函数的定义严格凸函数凸函数的推论:凹函数 常见凸函数凸函数的基本性质几种保持函数凸性的运算凸集与凸函数之间的关联关系 引言 本节将介绍凸函数定义及其基本性质。 本文是关于…...

【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag 使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库 1、删除指令 要删除指定的Git标签(版本号),您可以使用以下命令: git tag -d 标…...
)
thinkphp:数据库查询,嵌套别的表的查询(别的表做子查询)
例子 从 vendors 表中选择记录。在 vendors 表中,筛选出具有满足以下条件的 vendor_code 值: 对应的采购订单(在 po_headers_all 表中)存在未完全接收的采购行(在 po_lines_all 表中)。相应的采购订单状态…...

《Linux 系统命令及Shell脚本实践指南》
Linux 系统命令及Shell脚本实践指南 《Linux 系统命令及Shell脚本实践指南》该书从结构上分为三部分:第一部分1.1Linux的历史发展1.2用户管理1.3任务管理单一时刻执行一次任务使用at周期性任务使用:cron表达式,命令crontab 1.4文件管理1.4.1 Linux shell…...

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
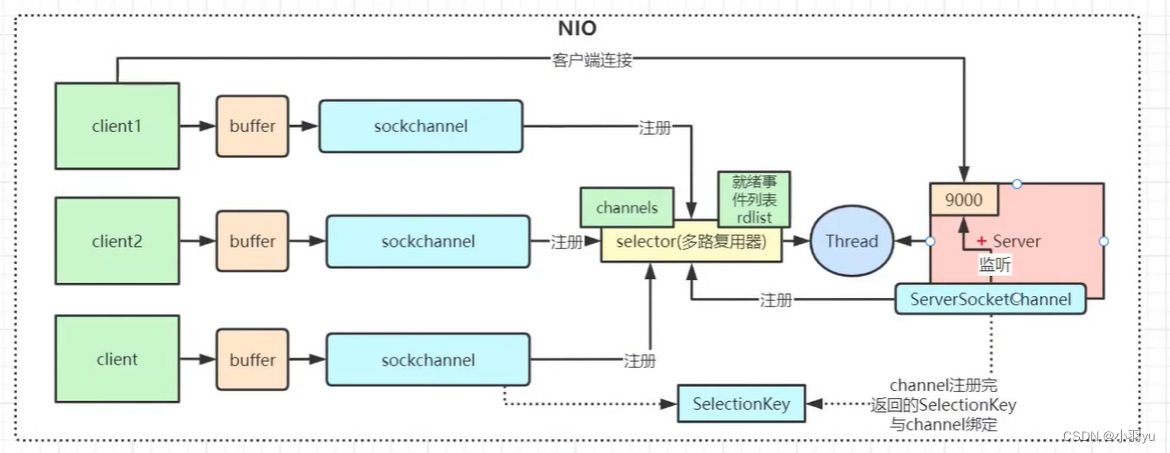
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

Python基础之高级函数
异常捕获 Python中,使用trycatch两个关键字来实现对异常的处理。在我们平时的工作中,异常的出现是在所难免的,但是异常一旦出现,极有可能会直接导致程序崩溃,无法正常运行,所以异常一定要及时的做出对应的…...
CSS3常用的新功能总结
CSS3常用的新功能包括圆角、阴渐变、2D变换、3D旋转、动画、viewpor和媒体查询。 圆角、阴影 border-redius 对一个元素实现圆角效果,是通过border-redius完成的。属性为两种方式: 一个属性值,表示设置所有四个角的半径为相同值ÿ…...
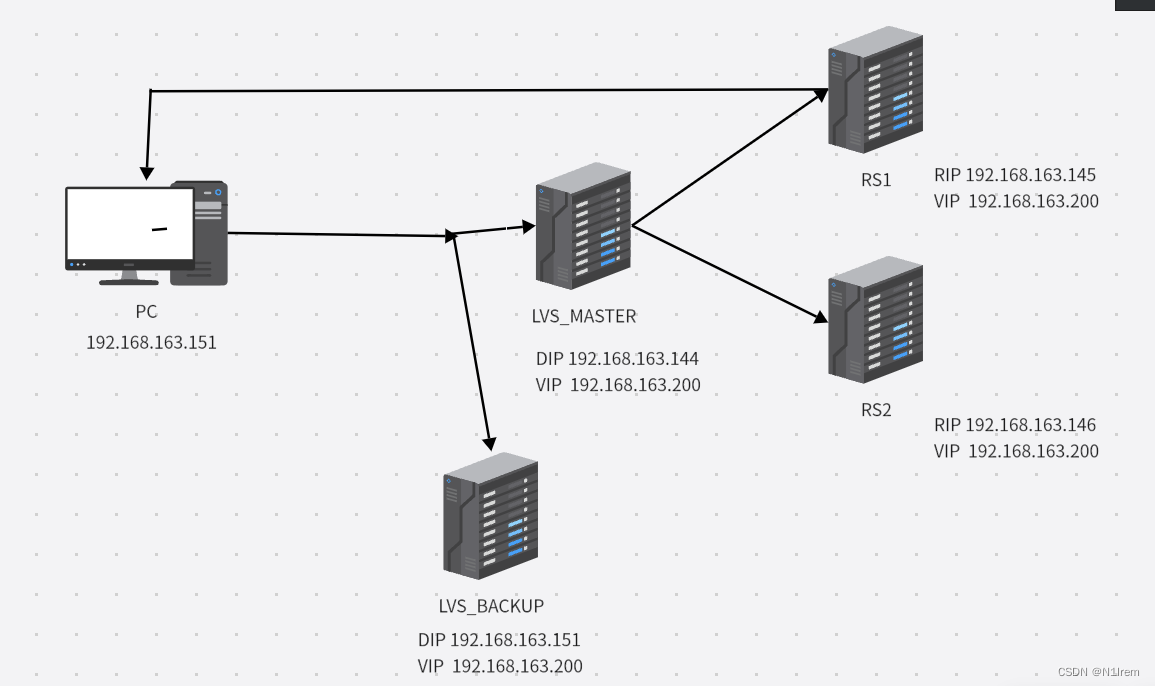
Lvs+KeepAlived高可用高性能负载均衡
目录 1.环境介绍 2.配置keepalived 3.测试 1.测试负载均衡 2.测试RS高可用 3.测试LVS高可用 3.1测试lvs主服务宕机 3.2.测试lvs主服务器恢复 4.我在实验中遇到的错误 1.环境介绍 环境:centos7 RS1---RIP1:192.168.163.145 VIP 192.168.163.200 RS2---RIP2…...

无涯教程-Android Online Test函数
Android在线测试模拟了真正的在线认证考试。您将看到基于 Android概念的多项选择题(MCQ),将为您提供四个options。您将为该问题选择最合适的答案,然后继续进行下一个问题,而不会浪费时间。完成完整的考试后,您将获得在线考试分数。 总问题数-20 最长时间-20分钟 Start Test …...

蓝桥杯打卡Day1
文章目录 全排列八皇后 一、全排列IO链接 本题思路:本题是一道经典的全排列问题,深度优先搜索即可解决。 #include <bits/stdc.h>constexpr int N10;std::string s; std::string ans; int n; bool st[N];void dfs(int u) {if(un){std::cout<<ans<…...

zipkin2.24.2源码install遇见的问题
1、idea导入项目后将Setting中的关于Maven和Java Compile相关的配置改为jdk11,同时Project Structure改为jdk11 2、将pom配置中的fork标签注释 标题未修改以上配置产生的问题 Compilation failure javac: Ч ı : --release : javac <options> <source files&g…...
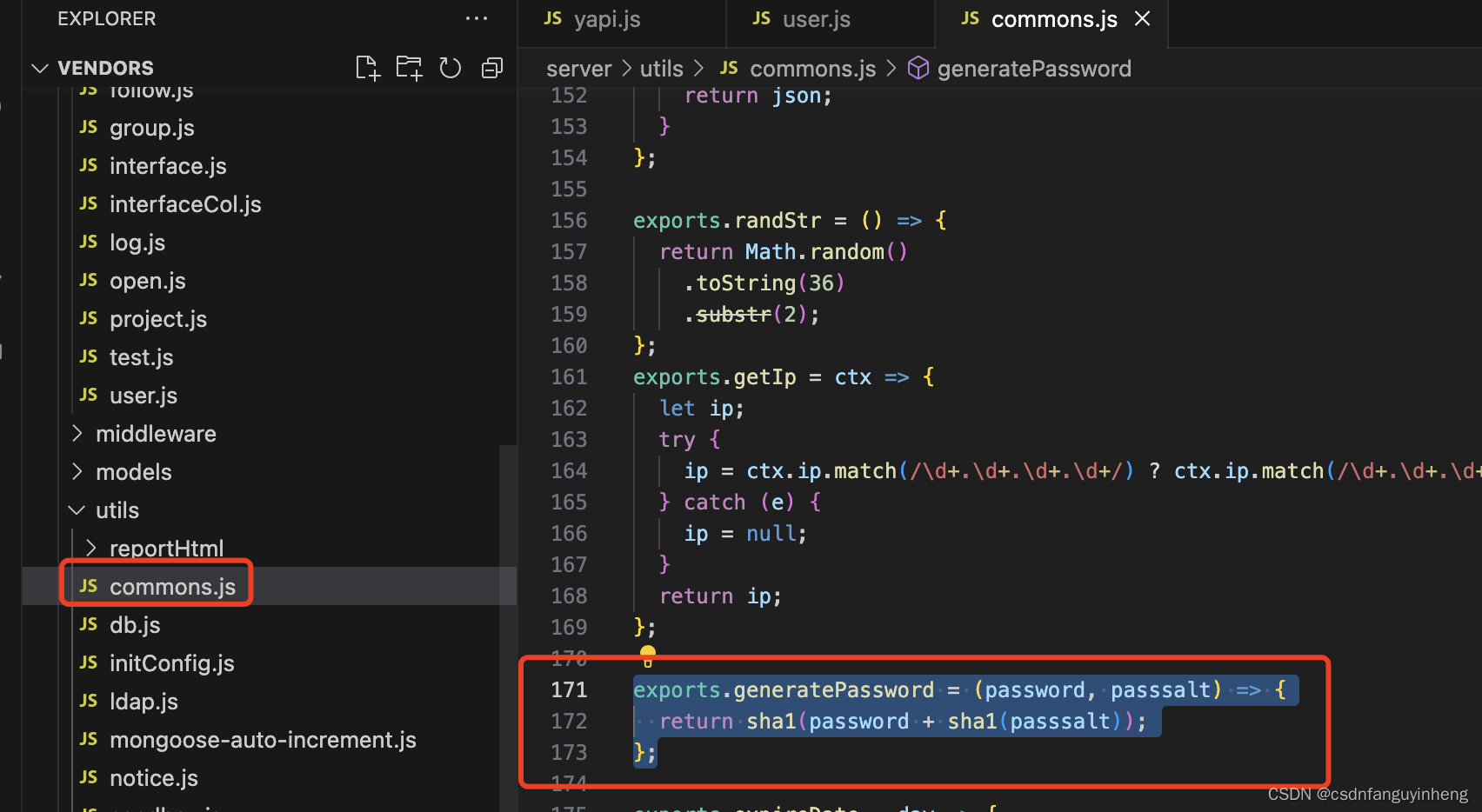
yapi密码是如何生成的
yapi密码是如何生成的 关闭yapi注册功能后,想要通过手动插入用户数据到db中,那么密码是如何生成的呢? exports.generatePassword (password, passsalt) > { return sha1(password sha1(passsalt)); }; 所以如果想要创建一个用户&#x…...

2023-09-02 LeetCode每日一题(最多可以摧毁的敌人城堡数目)
2023-09-02每日一题 一、题目编号 2511. 最多可以摧毁的敌人城堡数目二、题目链接 点击跳转到题目位置 三、题目描述 给你一个长度为 n ,下标从 0 开始的整数数组 forts ,表示一些城堡。forts[i] 可以是 -1 ,0 或者 1 ,其中&…...
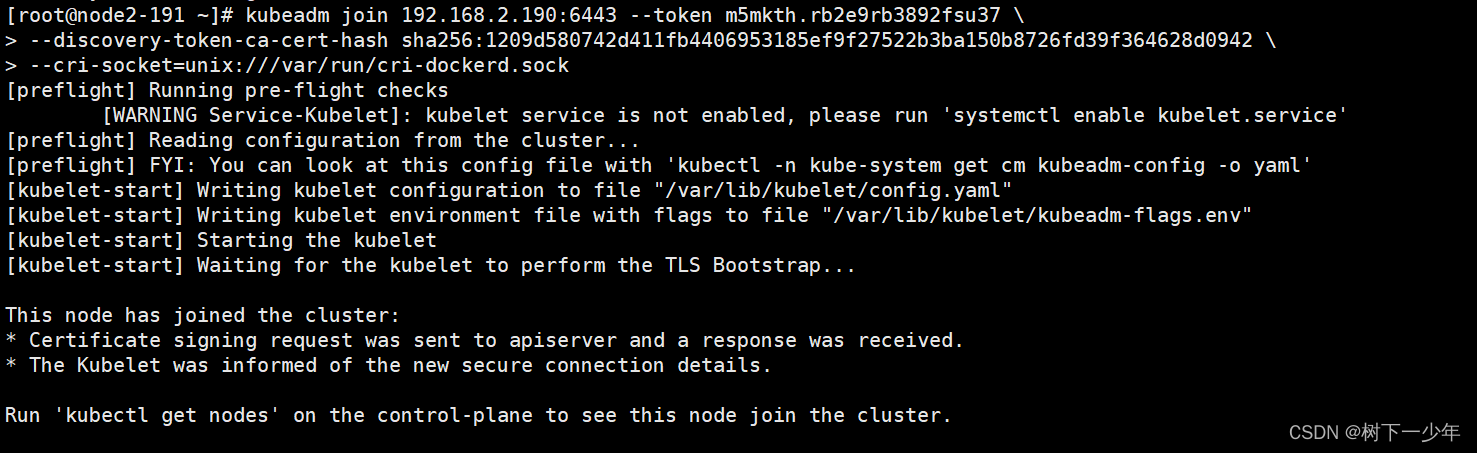
k8s环境部署配置
目录 一.虚拟机准备 二.基础环境配置(各个节点都做) 1.IP和hosts解析 2.防火墙和selinux 3.安装基本软件 4.配置时间同步 5.禁用swap分区 6.修改内核参数并重载 7.配置ipvs 三.docker环境(各个节点都做) 1.配置软件源并…...
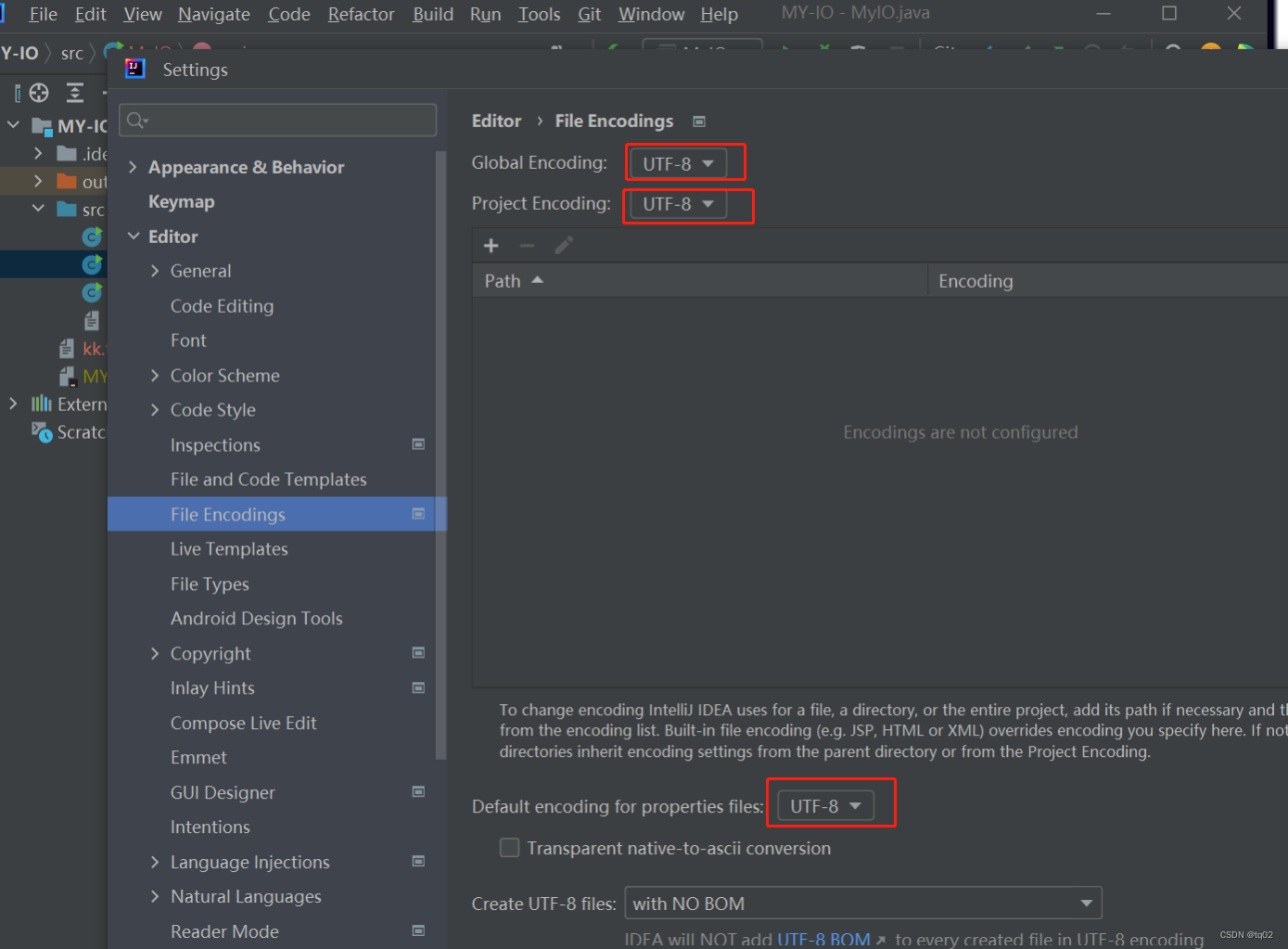
Java之文件操作与IO
目录 一.认识文件 1.1文件是什么? 1.2文件的组织 1.3文件路径 1.4文件的分类 二.文件操作 2.1File概述 三.文件内容操作--IO 3.1JavaIO的认识 3.2Reader和Writer ⭐Reader类 ⭐Writer类 3.2FileInputStream和FileOutputStream ⭐FileInputStream类 …...

指令系统(408)
一、拓展操作码指令格式 【2017 统考】某计算机按字节编址,指令字长固定且只有两种指令格式,其中三地址指令29条、二地址指令107条,每个地址字段6位,则指令字长至少应该是( A) A、24位 B、26位 …...
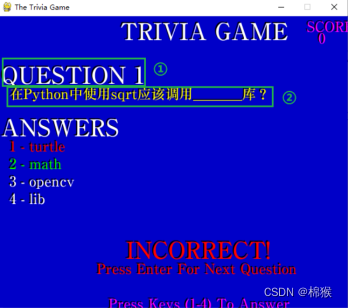
Pygame中Trivia游戏解析6-3
3.3 Trivia类的show_question()函数 Trivia类的show_question()函数的作用是显示题目。主要包括显示题目框架、显示题目内容和显示题目选项等三部分。 3.3.1 显示题目的框架 在show_question()函数中,通过以下代码显示题目的框架。 print_text(font1, 210, 5, &q…...
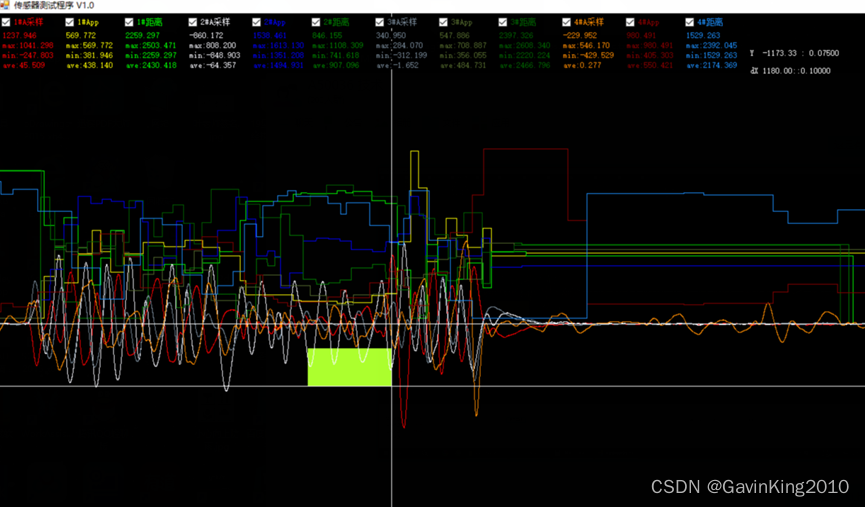
热释电矢量传感器设计
1 概述 使用4个热释电传感器组成一个2X2的矩阵。通过曲线的相位差、 峰峰值等特征量来计算相关信息。本文使用STM32单片机设计、制作了热释电传感器矩阵;使用C#.NET设计了上位机软件。为以上研究做了试验平台。 2 硬件电路设计 2.1 热释电传感器介绍 热释电红外…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
