层次分析法(matlab实现)
1.层次分析法(AHP)
在决策理论中,层次分析法是一种以数学和心理学为基础,组织和分析复杂决策的结构化技术,它代表了一种量化决策标准权重的准确方法,通过成对比较,利用个别专家的经验来估计因素的相对大小
2.算法用途
在很多情况下,我们对事物的评价,应该多维度的进行评价。多维度评价之后我们要如何把它们合并成一个指标用于比较事物的好坏?这时候需要对各个指标赋权,层次分析法就是用来赋权重的,这个方法个体主观性较强,在数据集比较小,实在不好比较的时候可以选择这种方法
3.算法简述
这个算法是一个多指标综合评价算法,这种算法一般会有两个用途:
- 指标定权
我们可以在没有数据支撑的情况下可以根据每个人对重视程度不一样而给各个指标指定权重
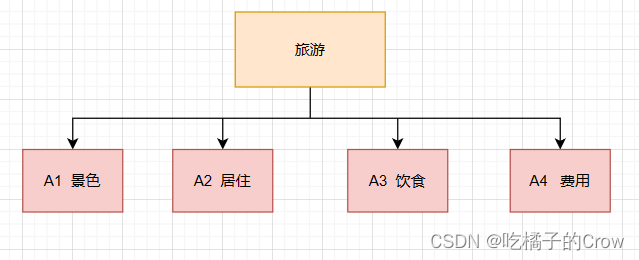
- 量化方案选择
我们在旅游的时候,可能会面临去哪的难题,我们会假设有几套方案,例如:杭州、三亚、成都,而每个地方的都可以综合以上的4个因素,给这些方案计算出一个量化得分,然后我们就可以根据它们各自的得分得出我们心里的最优选择
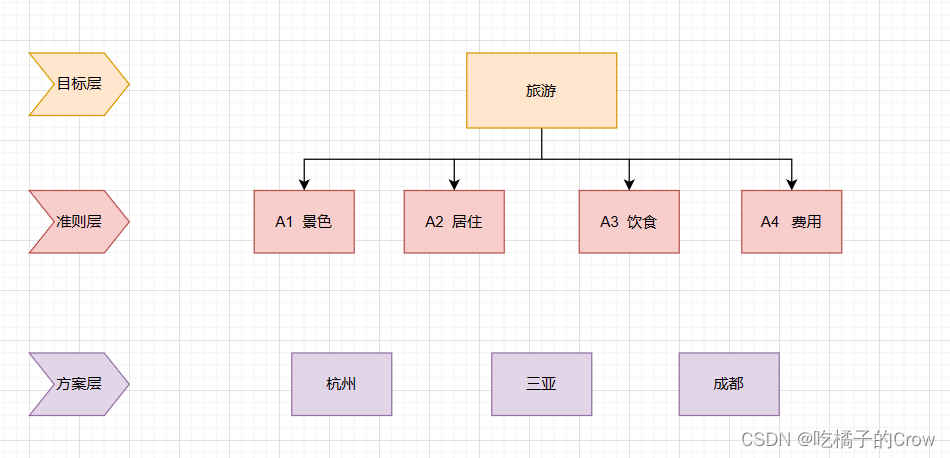
4.AHP层次分析过程
在分析一个现象或者问题之前,首先将现象或问题根据它们的性质分解成有关因素,并根据它们之间的关系分类而形成一个多层次的结构模型,然后通过经验或者专家,来判断和衡量底层因素对高层因素的相对重要性,并根据重要性的程度得出权重排序,进而可以量化分析比较。
层次分析法的核心是将影响因素层次化和数据化,它把一个抽象的现象或问题由难到易的予以分解,易于对复杂问题进行直观的判断并做出决策。层次分析法具有将复杂问题简单化且计算简单等优点,应用都十分广泛,诸如在人员素质评估、多方案比较、科学成果评比和工作成效评价等多领域多方面都有运用
一般的层次分析法分为三层:
- 目标层(分析目的)
- 准则层(分析因素)
- 方案层(分析种类)
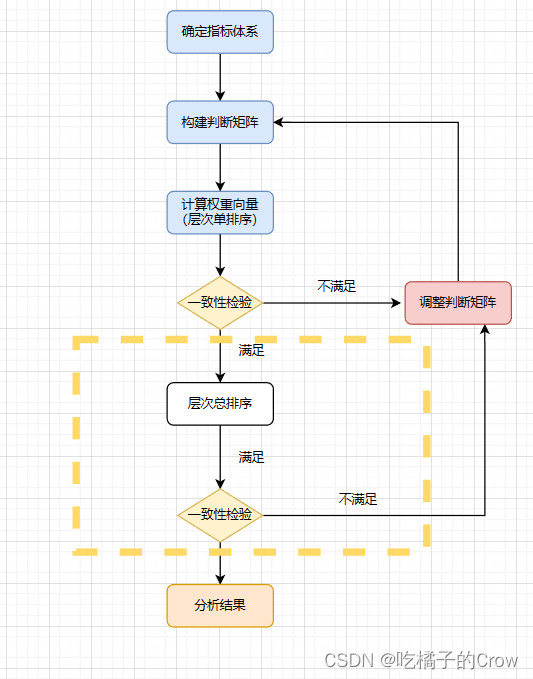
注意:一致性检验的含义用于确定构建构建的判断矩阵是否存在逻辑问题
类似于A对于B是3,就说明A比B重要,A对于C是1/3,就说明C比A重要,那么如果B对于C是2的话,就说明B比C重要,但是根据上述的逻辑,这样就犯了逻辑性的错误,理应是C比B重要
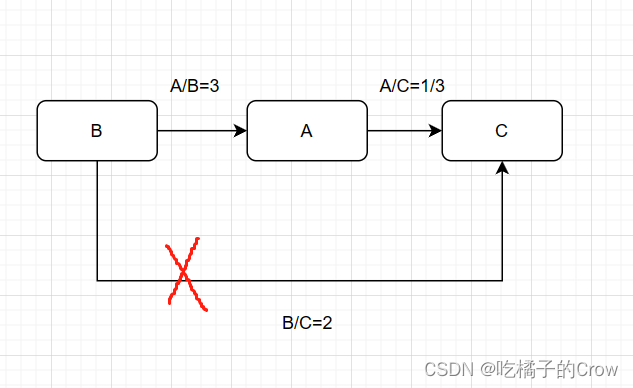
4.1 构建层次评价模型
我们应该在分析前先确认整个决策事件的目标层、准则层、方案层

4.2构造判断矩阵
构造判断矩阵就是通过各要素之间相互两两比较,并确定各准则层对目标的权重
| 标度 | 含义 |
| 1 | 表示两个元素相比,具有同样的重要性 |
| 3 | 表示两个元素相比,前者比后者稍重要 |
| 5 | 表示两个元素相比,前者比后者明显重要 |
| 7 | 表示两个元素相比,前者比后者极其重要 |
| 9 | 表示两个元素相比,前者比后者强烈重要 |
| 2,4,6,8 | 表示上述相邻判断的中间值 |
| 1~9的倒数 | 表示相应两因素交换次序比较的重要性 |
判断矩阵满足:

我们可以对于准则A,可以构造一个:
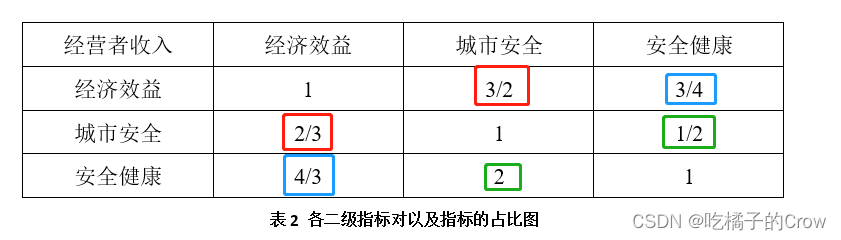
我们就可以根据我们对这些因素的一个客观认识去得到这个完整的判断矩阵
4.3 层次单排序与一致性检验
4.3.1层次单排序
所谓的层次排序法就是根据我们构成的判别矩阵,求解各个指标的权重
方法一:方根法
- 计算每行乘积得到m次方,得到一个m维向量
- 将向量标准即为权重向量,即得到权重
方法二:和法
- 先将矩阵的每列进行标准化
- 将标准化后的各元素按行求和
- 将求和结果进行标准化

4.3.2 求解最大特征值与CI值
设 n 阶判断矩阵为 B,则可用以下方法求出其最大的特征根 :BW=λW,其中,W 是 B 的特征向量。 在层次分析法中, 我们用以下的一致性指标 CI 来检验判断的一致性指标 (Consistency Index):
CI=0表示判断矩阵完全一致,CI越大,判断矩阵的不一致性程度越严重
当得出权重矩阵后,我们可以计算最大特征根,其公式为:
其中n为维度数,AW为判断矩阵标准化后的权重,然后按行的累加值
4.3.3 根据CI、RI值求解CR值,判断其一致性是否通过

情况如下:
- CR<0.1时,矩阵A的一致性程度被认为在容许的范围内
- CR>=0.1时,我们应该考虑对矩阵A进行修正
4.3.4 层次总排序与一致性检验
计算某一层所有因素对于最高层(目标层)相对重要性的权值,称为层次总排序
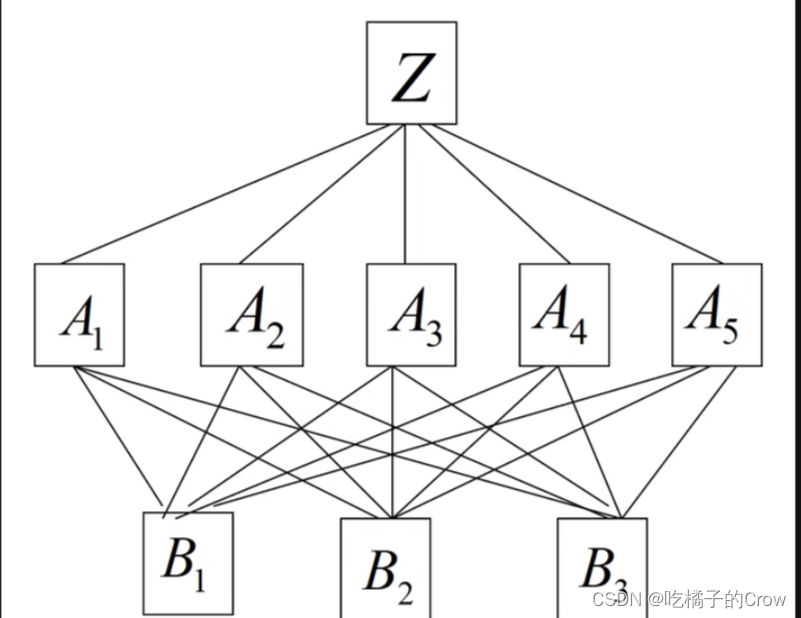

案例分析:


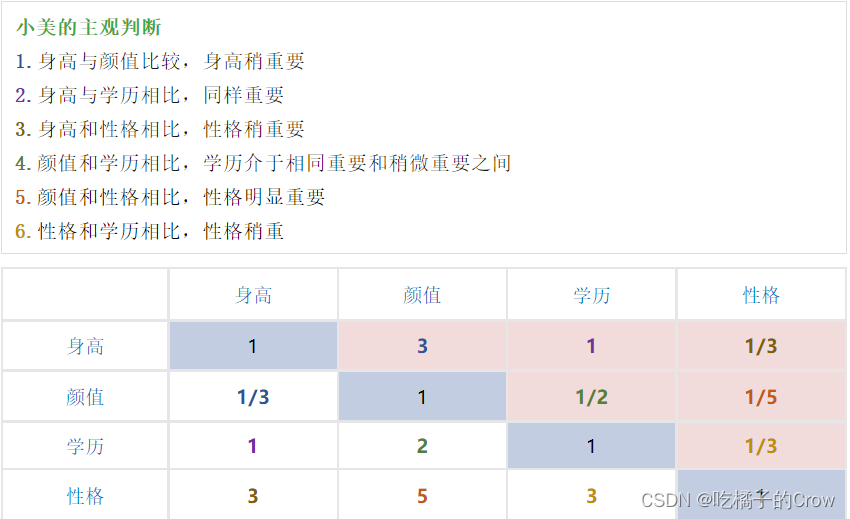


matlab源码:
%层次分析法
%P是指标评分 B是判别矩阵
function level(P,A)
%求出判别矩阵的行列数
[n,~]=size(A);
%求出该矩阵的特征向量与特征值
[V,D]=eig(A)
tzz=max(max(D))%找出最大的特征值
c1=D(1,:)==tzz%找出最大的特征值的位置
tzx=V(:,c1)%最大特征值对应的特征向量
%赋权重
quan=zeros(n,1)
%得到权重向量
for i=1:nquan(i,1)=tzx(i,1)/sum(tzx);
end
Q=quan
%--------------------------------一致性检验---------------------------------
%计算一致性指标CI
CI=(tzz-n)/(n-1)
%平均随机一致性指标RI
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判断是否通过一致性
CR=CI/RI(1,n)
if CR>=0.1fprintf('没有通过一致性\n');
elsefprintf('通过一致性检验\n');
end
%显示出所有评分对象的评分值
score=P*Q;
for i=1:length(score)name=['object_score',num2str(i)];eval([name,'=score(i)'])
end相关文章:

层次分析法(matlab实现)
1.层次分析法(AHP) 在决策理论中,层次分析法是一种以数学和心理学为基础,组织和分析复杂决策的结构化技术,它代表了一种量化决策标准权重的准确方法,通过成对比较,利用个别专家的经验来估计因素…...

python selenium 自动化登录页面
去掉自动化标识,绕过js,绕过ip import time from selenium import webdriver from selenium.webdriver.chrome.options import Options# 去掉自动化标识,绕过js option Options() option.add_experimental_option(excludeSwitches, [enable…...

【Linux】高级IO --- 多路转接,select,poll,epoll
所有通过捷径所获取的快乐,无论是金钱、性还是名望,最终都会给自己带来痛苦 文章目录 一、五种IO模型1.什么是高效的IO?(降低等待的时间比重)2.有哪些IO模型?哪些模型是高效的?3.五种IO模型的特…...
anaconda navigator打不开,一直在loading画面
anaconda navigator打不开,一直在loading画面。百度解决方法,用网上的方法在命令窗口里运行conda update anaconda结果一直显示 solving environment卡在那里。又尝试用管理员身份运行还是不行,打开后出现There in aninstance of Anaconda Na…...
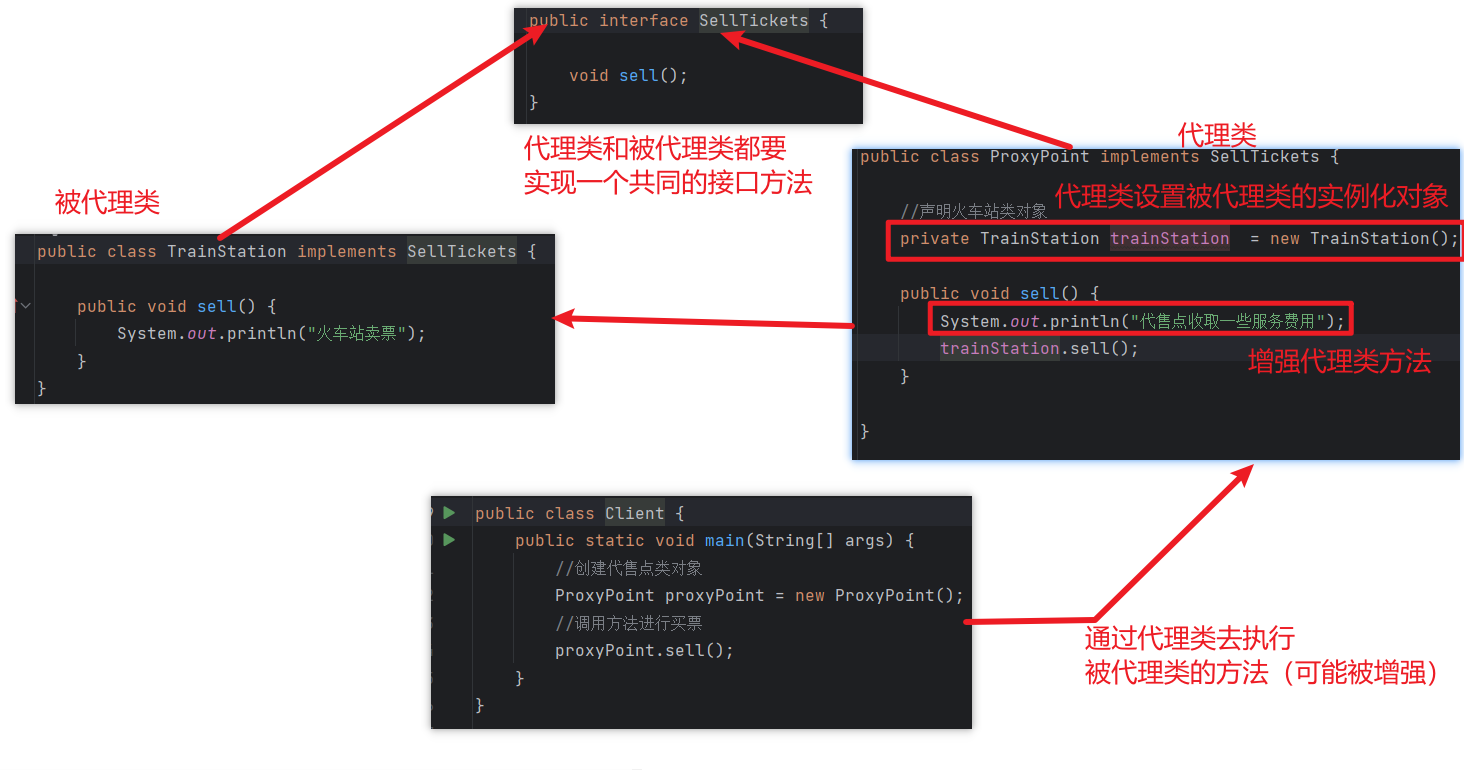
【Java基础】深入理解反射、反射的应用(工厂模式、代理模式)
文章目录 1. Java反射机制是什么?1.2 Java反射例子 2. Java反射机制中获取Class的三种方式及区别?3. Java反射机制的应用场景有哪些?3.1. 优化静态工厂模式(解耦)3.1.1 优化前(工厂类和产品类耦合ÿ…...

VUE 项目 nginx部署
server {listen 80; # 监听的端口号server_name 129.204.189.149; # 服务器的ip或者域名#charset koi8-r;#access_log logs/host.access.log main;# 前端服务反向代理配置location / {proxy_http_version 1.1;proxy_set_header Host $host;proxy_set_header X-Real-…...
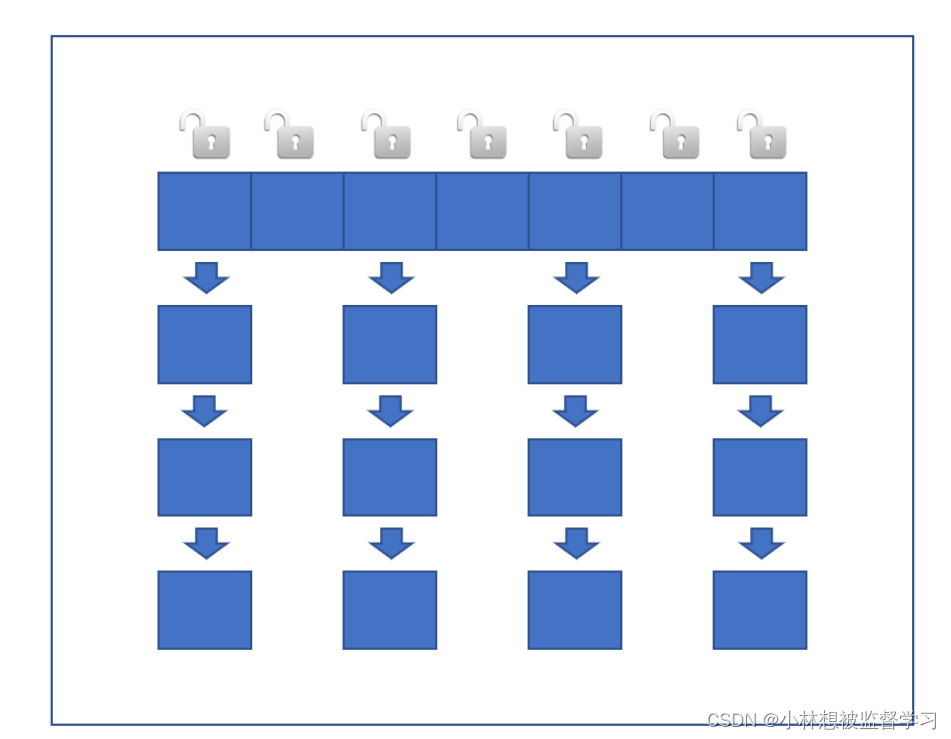
Hashtable和HashMap、ConcurrentHashMap 之间的区别
Hashtable和HashMap的区别 HashMap和Hashtable都是哈希表数据结构,但是Hashtable是线程安全的,HashMap是线程不安全的 Hashtable实现线程安全就是简单的把关键方法都加上了synchronized关键字 直接在方法上添加synchronized相当于针对this对象࿰…...

包管理工具--》npm的配置及使用(二)
在阅读本篇文章前请先阅读包管理工具--》npm的配置及使用(一) 目录 🌟语义版本 避免还原的差异 npm的差异版本处理 🌟npm 脚本 (npm scripts) 🌟运行环境配置 在node中读取package.json …...

【Linux】多线程2——线程互斥与同步/多线程应用
文章目录 1. 线程互斥1.1 问题引入1.2 线程互斥的相关概念1.3 互斥量mutex1.4 互斥量实现原理1.5 死锁 2. 线程安全和可重入函数3. 线程同步3.1 同步概念3.2 条件变量 4. 生产消费模型4.1 基于阻塞队列的cp模型4.2 基于环形队列的cp模型POSIX信号量 5. 线程池5.1 互斥量RAII版本…...

Python中的函数式编程是什么?
Python中的函数式编程是一种编程范式,它强调使用纯函数和避免可变状态来构建程序。函数式编程的核心思想是将计算视为函数的求值,而不是通过改变状态来实现。在函数式编程中,函数被视为一等公民,可以作为参数传递给其他函数&#…...
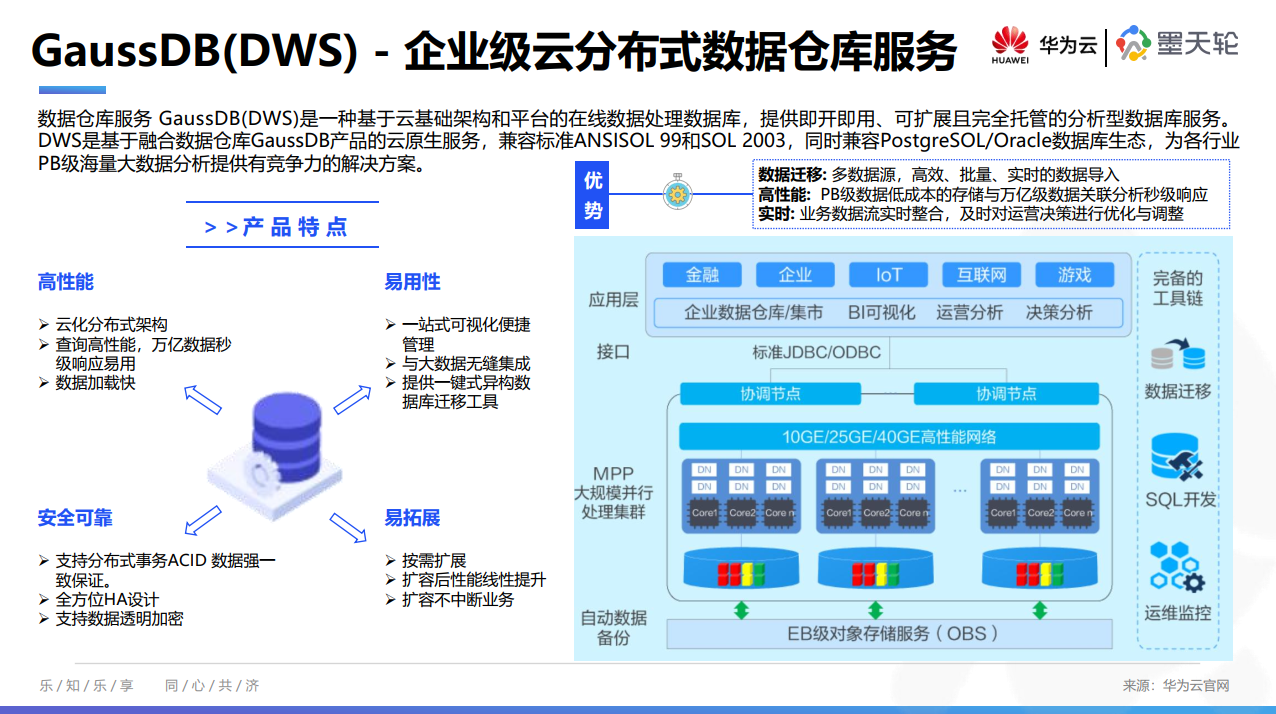
8月《中国数据库行业分析报告》已发布,聚焦数据仓库、首发【全球数据仓库产业图谱】
为了帮助大家及时了解中国数据库行业发展现状、梳理当前数据库市场环境和产品生态等情况,从2022年4月起,墨天轮社区行业分析研究团队出品将持续每月为大家推出最新《中国数据库行业分析报告》,持续传播数据技术知识、努力促进技术创新与行业生…...
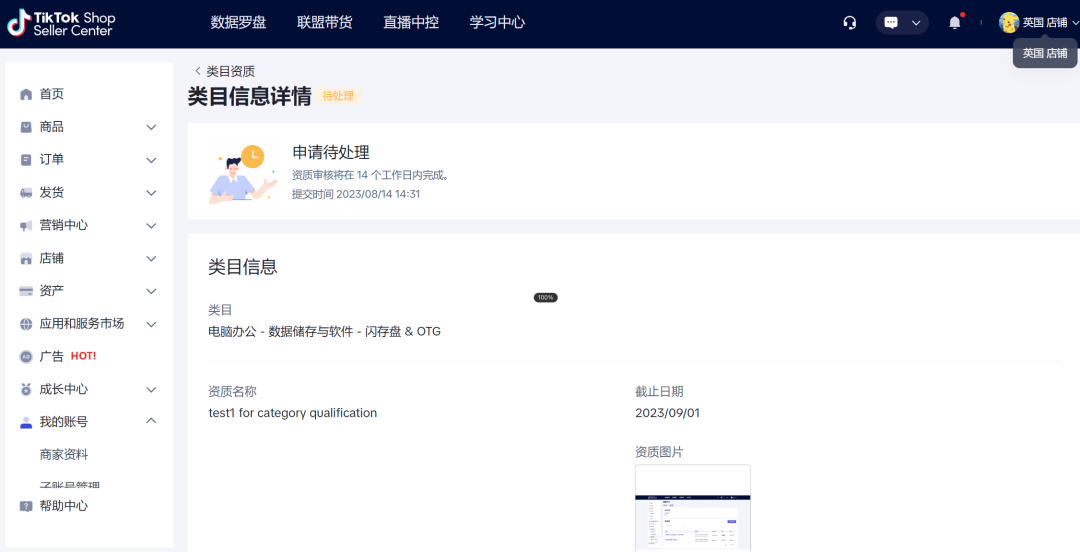
TikTok Shop|如何成为定邀卖家?
TikTok在商品售卖资质和商家资质上做了很多限制,比如我们熟知的珠宝类目,今天我们结合TikTok Shop规则中心8月30号发布的《如何申请成为“定邀”卖家》和关于“定邀”商品的政策进行分析,看看如何成为“定邀”卖家。 定邀商品/类目有哪些&am…...

C++二级题目6
数字放大 #include<iostream> #include<string.h> #include<stdio.h> #include<iomanip> #include<cmath> #include<bits/stdc.h> int a[2000][2000]; int b[2000]; char c[2000]; long long n; using namespace std; int main() {int x;…...
南方科技大学博士研究生奖助学金,深圳大学
目录 南方科技大学 中南大学 南京大学 厦门大学 苏州大学 中南财经政法大学 深圳大学 南方科技大学 https://ocean.sustech.edu.cn/ocean/public/upload/download/3/2.pdf 南方科技大学的在读研究生,每人每年都会得到40000元的补助,这40000块钱分…...
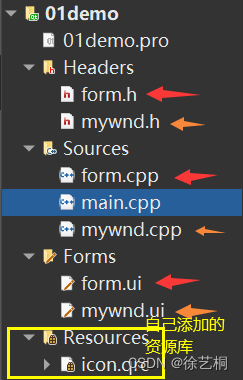
QT 使用信号与槽实现界面跳转
一、创建一个新的页面 1 > 在原有工程上新建一个页面 2 > 选择Qt - Qt 设计师界面类 - choose 3 > 选择Widget模板 - 下一步 4 > 输入自定义类名 - 下一步 会自动生成其同名的.h .cpp .ui文件 5 > 最终效果 Headers存放.h文件 Soueces存放.cpp文件 Forms存放.u…...
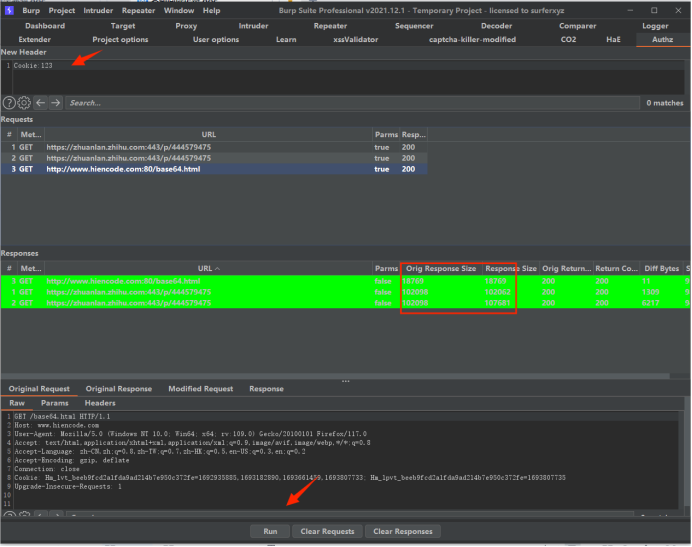
Burp插件HaE与Authz用法
HaE与Authz均为BurpSuite插件生态的一员,两者搭配可以避免“越权”、“未授权”两类漏洞的重复测试行为。(适用于业务繁杂,系统模块功能多的场景) 两个插件都可以在store里安装 安装完后,点击Filter Settings勾选Sho…...
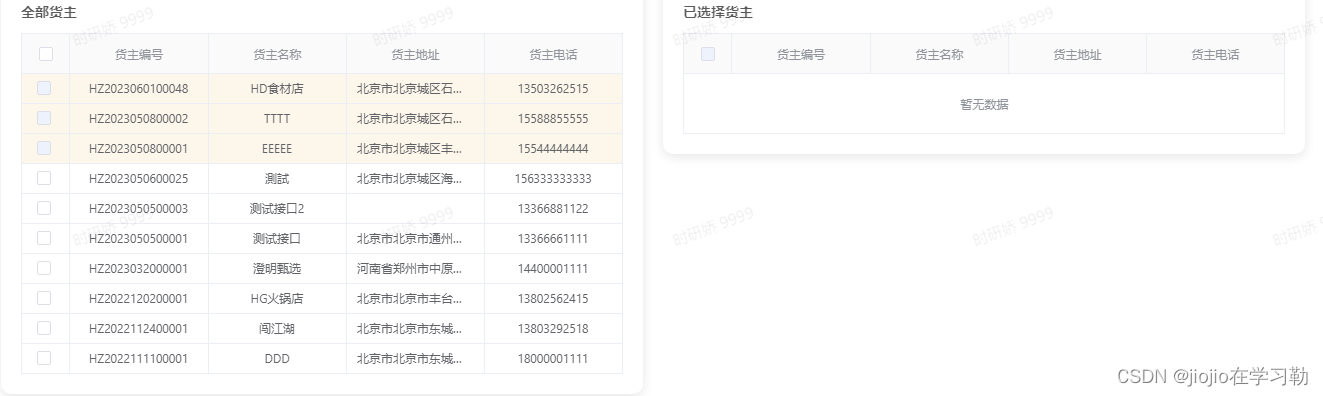
element+vue table表格全部数据和已选数据联动
1.组件TableChoose <template><div class"tableChooseBox"><div class"tableRow"><div class"tableCard"><div class"tableHeadTip">全部{{ labelTitle }}</div><slot name"body" …...

vue 防抖与节流用法
一、html <template><button click"getData">获取数据</button> </template>二、JS import { throttle } from "/utils/common"; export default {methods:{getData: throttle(async function(params){console.log(”获取接口数…...
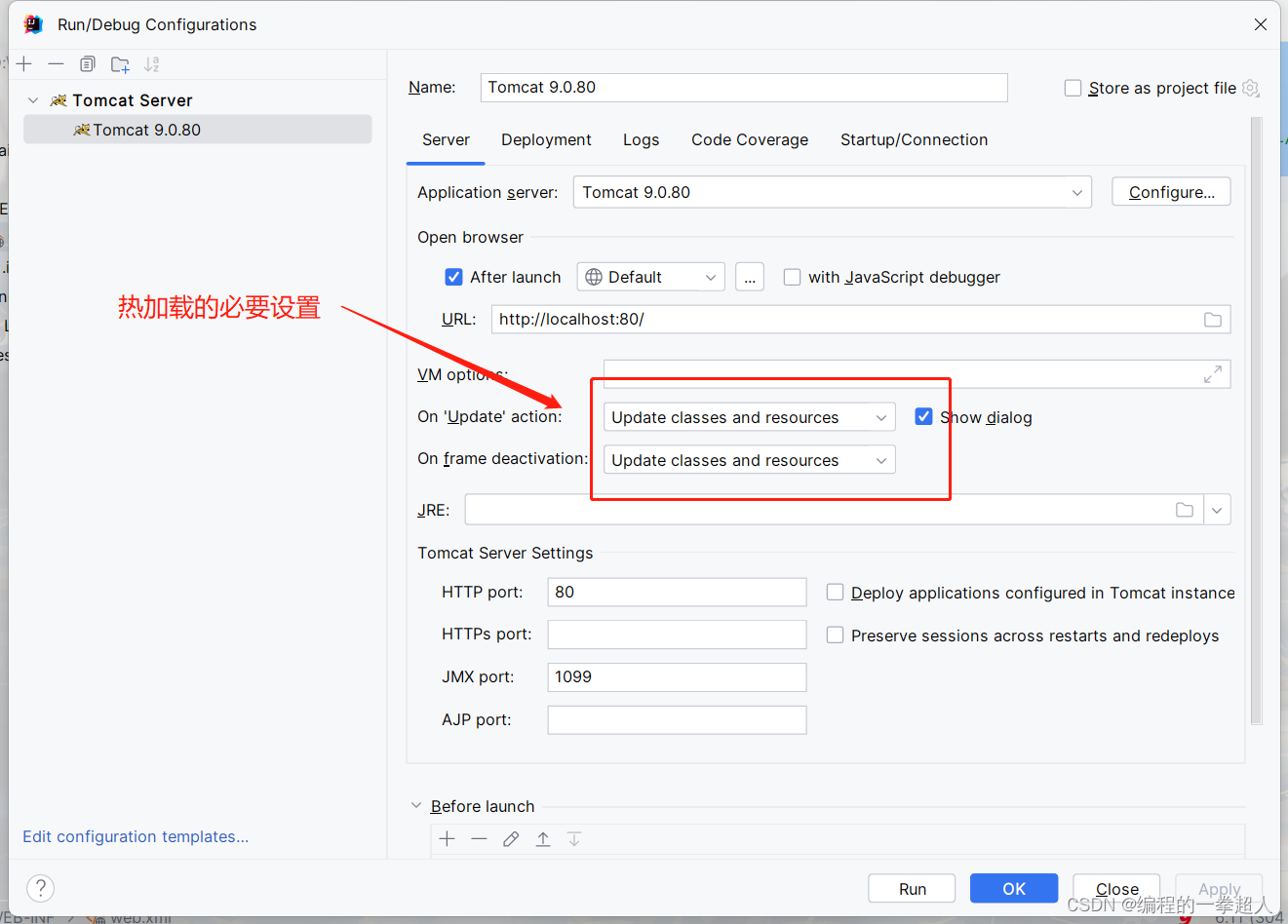
IntelliJ IDEA创建Web项目并使用Web服务器----Tomcat
🏆IntelliJ IDEA创建Web项目并使用Web服务器----Tomcat 以下是本篇文章正文内容,下面案例可供参考(提示:本篇文章属于原创,请转发或者引用时注明出处。),大家记得支持一下!ÿ…...

rk3399 linux 5.10 usb 2.0设备上电概率性注册失败
多次开关机,发现usb hub和4G都通信失败了,这就有点奇怪了,按理说usb驱动是没啥问题的 先查看usb log rootlinaro-alip:/# dmesg | grep usb [ 1.723797] usbcore: registered new interface driver usbfs [ 1.723828] usbcore: regis…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
