ACM中的数论
ACM中的数论是计算机科学领域中的一个重要分支,它主要研究整数的性质、运算规律和它们之间的关系。在ACM竞赛中,数论问题经常出现,因此掌握一定的数论知识对于参加ACM竞赛的选手来说是非常重要的。本文将介绍一些常见的数论概念和方法,以及如何应用它们解决实际问题。
一、基本数论概念
质数:一个大于1的自然数,除了1和它本身以外没有其他因数的数称为质数。例如2、3、5、7等。
合数:一个大于1的自然数,如果它不是质数,那么就是合数。例如4、6、8、9等。
最大公约数:两个或多个整数共有约数中最大的一个。例如,12和16的最大公约数是4。
最小公倍数:两个或多个整数共有倍数中最小的一个。例如,12和16的最小公倍数是48。
欧几里得算法:一种求最大公约数的算法,通过辗转相除法求解。
二、数论方法
素性测试:判断一个数是否为质数的方法。常用的素性测试方法有费马小定理、米勒-拉宾素性检验、阿特金森-桑德斯素性检验等。
同余方程:形如x≡a(mod m)的方程,其中x是整数,a和m是已知整数。求解这类方程的方法称为同余方程的解法。常用的同余方程解法有中国剩余定理、扩展欧几里得算法等。
离散对数问题:给定一个整数n和一个整数g,求解满足ax^2+by=n的整数解(x,y)的数量。这个问题可以通过扩展欧几里得算法和模重复平方算法求解。
大整数乘法取模:给定两个大整数a和b以及一个模数m,求a乘以b后模m的结果。这个问题可以通过快速幂算法和二进制算法求解。
三、实际应用
密码学:在密码学中,很多加密算法都涉及到大整数的乘法和取模运算,例如RSA加密算法、椭圆曲线加密算法等。了解这些算法的原理有助于理解它们的加密原理。
编码理论:在信息论中,有很多问题可以转化为求最短编码长度的问题。了解编码理论可以帮助我们设计出更高效的编码方案。
图论:在图论中,很多问题可以转化为求最短路径的问题。了解最短路径问题的解决方法可以帮助我们设计出更好的网络拓扑结构。
相关文章:

ACM中的数论
ACM中的数论是计算机科学领域中的一个重要分支,它主要研究整数的性质、运算规律和它们之间的关系。在ACM竞赛中,数论问题经常出现,因此掌握一定的数论知识对于参加ACM竞赛的选手来说是非常重要的。本文将介绍一些常见的数论概念和方法&#x…...
我的创作纪念日 —— 一年之期
前言 大家好!我是荔枝嘿~看到官方私信才发现原来时间又过去了一年,荔枝也在CSDN中创作满一年啦,虽然中间因为种种原因并没有经常输出博文哈哈,但荔枝一直在坚持创作嘿嘿。记得去年的同一时间我也同样写了一篇总结文哈哈哈&#x…...
qt.qpa.plugin:找不到Qt平台插件“wayland“|| (下载插件)Ubuntu上解决方案
相信大家也都知道这个地方应该做什么,当然是下载这个qt平台的插件wayland,但是很多人可能不知道怎么下载这个插件。 那么我现在要说的这个方法就是针对这种的。 sudo apt install qtwayland5完事儿了奥兄弟们。 看看效果 正常了奥。...

详解Spring Boot中@PostConstruct的使用
PostConstruct 在Java中,PostConstruct是一个注解,通常用于标记一个方法,它表示该方法在类实例化之后(通过构造函数创建对象之后)立即执行。 加上PostConstruct注解的方法会在对象的所有依赖项都已经注入完成之后执行…...

判断子序列
判断子序列 题目: 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"…...
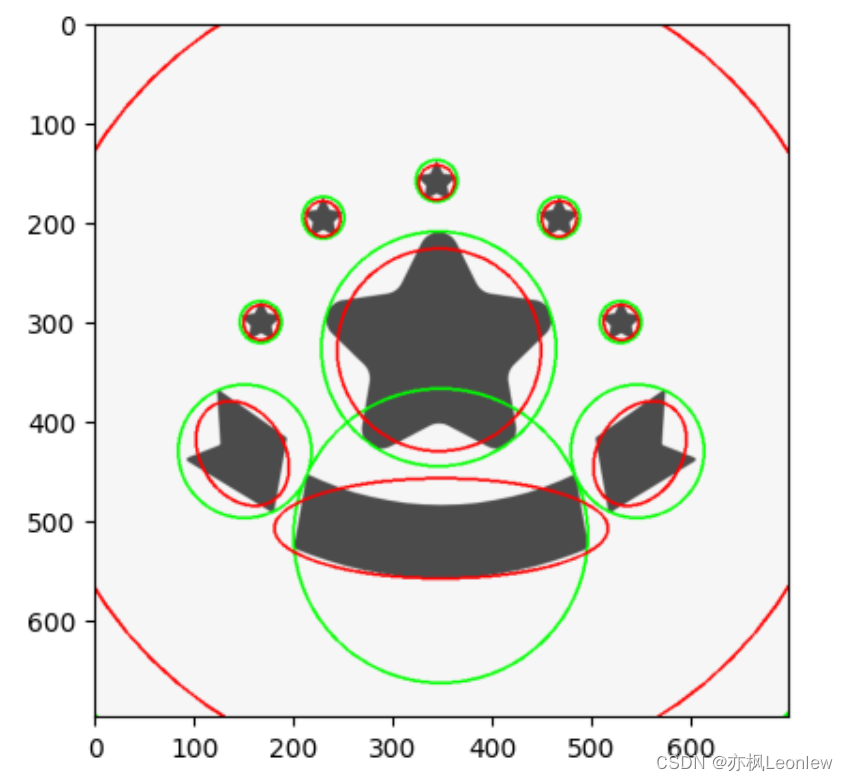
Python Opencv实践 - 轮廓特征(最小外接圆,椭圆拟合)
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/stars.PNG") plt.imshow(img[:,:,::-1])#轮廓检测 img_gray cv.cvtColor(img, cv.COLOR_BGR2GRAY) ret,thresh cv.threshold(img_gray, 127, 255, 0) contou…...

Ubuntu22.04 LTS+NVIDIA 4090+Cuda12.1+cudnn8.8.1
系统环境中: 1.系统驱动安装的是: NVIDIA-Linux-x86_64-530.30.02.run 2.CUDA安装:cuda_12.1.0_530.30.02_linux.run(无需第1步,直接安装它就带配套驱动) wget https://developer.download.nvidia.com/…...
重装系统后,MySQL install错误,找不到dll文件,或者应用程序错误
文章目录 1.找不到某某dll文件2.mysqld.exe - 应用程序错误使用DX工具直接修复 1.找不到某某dll文件 由于找不到VCRUNTIME140_1.dll或者MSVCP120.dll,无法继续执行代码,重新安装程序可能会解决此问题。 在使用一台重装系统过的电脑,再次重新…...
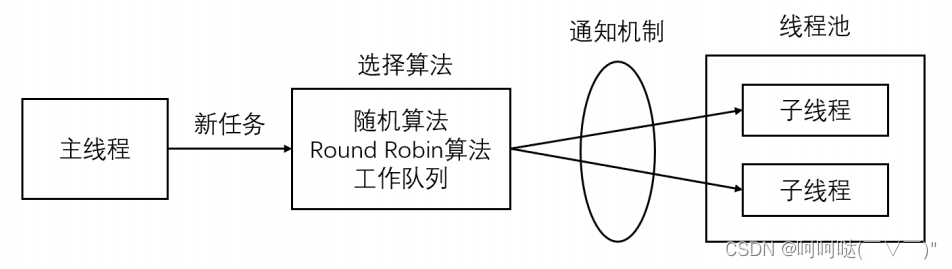
线程同步机制类封装及线程池实现
1.线程池 线程池是由服务器预先创建的一组子线程,线程池中的线程数量应该和 CPU 数量差不多。线程池中的所有子线程都运行着相同的代码。当有新的任务到来时,主线程将通过某种方式选择线程池中的某一个子线程来为之服务。相比与动态的创建子线程&#x…...

Linux中的用户、组和权限
一,Linux的安全模型 1.安全3A Authentication(认证),Authorization(授权),Accounting(审计)(AAA)是用于对计算机资源的访问、策略执行、审计使用情况和提供服务账单所需信息等功能进行智能控制的基本组件的一个术语。大多数人认为这三个组合的过程对有效的网络管理和…...

python学习--基本数据类型之字典
python中数据类型 第一类:不可变类型、静态数据类型、不支持增删改操作 数字(number)字符串(string)元组(tuple) 第二类:可变类型、动态数据类型、支持增删改操作 列表ÿ…...
【OpenCV入门】第九部分——模板匹配
文章结构 模板匹配方法单模板匹配单目标匹配多目标匹配 多模板匹配 模板匹配方法 模板是被查找的图像。模板匹配是指查找模板在原始图像中的哪个位置的过程。 result cv2.matchTemplate(image, templ, method, mask)image: 原始图像templ: 模板图像&a…...

在设计web页面时,为移动端设计一套页面,PC端设计一套页面,并且能自动根据设备类型来选择是用移动端的页面还是PC端的页面。
响应式设计,即移动端和PC端共用一个HTML模式,网站的程序和模板自动根据设备类型和屏幕大小进行自适应调整。这种方法我不喜欢,原因是不能很好保证各种客户端的效果,里面存在各种复杂的兼容性等问题。 我喜欢为不同的客户端写不同的…...
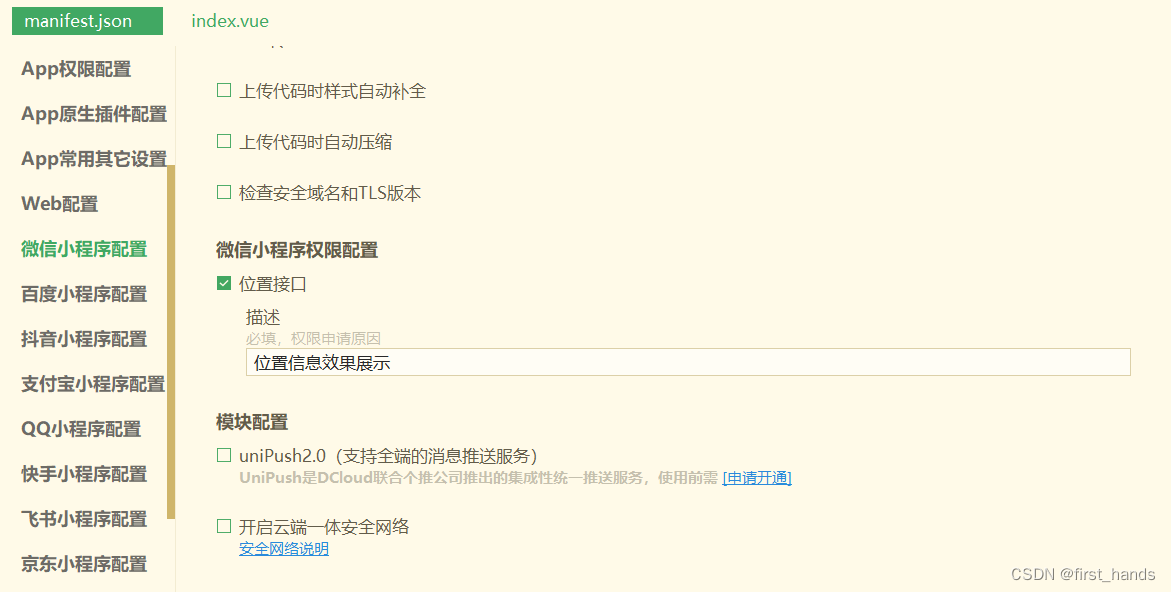
微信小程序地图应用总结版
1.应用场景:展示公司位置,并打开第三方app(高德,腾讯)导航到目标位置。 (1)展示位置地图 uniapp官网提供了相关组件,uniapp-map组件https://uniapp.dcloud.net.cn/component/map.ht…...
分支创建查看切换
1、初始化git目录,创建文件并将其推送到本地库 git init echo "123" > hello.txt git add hello.txt git commit -m "first commit" hello.txt$ git init Initialized empty Git repository in D:/Git/git-demo/.git/ AdministratorDESKT…...

参编三大金融国标,奇富科技以技术促行业规范化演进
近期,由中国互联网金融协会领导制定的《互联网金融智能风险防控技术要求》《互联网金融个人网络消费信贷信息披露》《互联网金融个人身份识别技术要求》三项国家标准颁布,由国家市场监督管理总局、国家标准化管理委员会发布,奇富科技作为核心…...

芯片开发之难如何破解?龙智诚邀您前往DR IP-SoC China 2023 Day
2023年9月6日(周三),龙智即将亮相D&R IP-SoC China 2023 Day,呈现集成了Perforce与Atlassian产品的芯片开发解决方案,助力企业更好、更快地进行芯片开发。 龙智资深顾问、技术支持部门负责人李培将带来主题演讲—…...
Gof23设计模式之策略模式
1.概述 该模式定义了一系列算法,并将每个算法封装起来,使它们可以相互替换,且算法的变化不会影响使用算法的客户。策略模式属于对象行为模式,它通过对算法进行封装,把使用算法的责任和算法的实现分割开来,…...
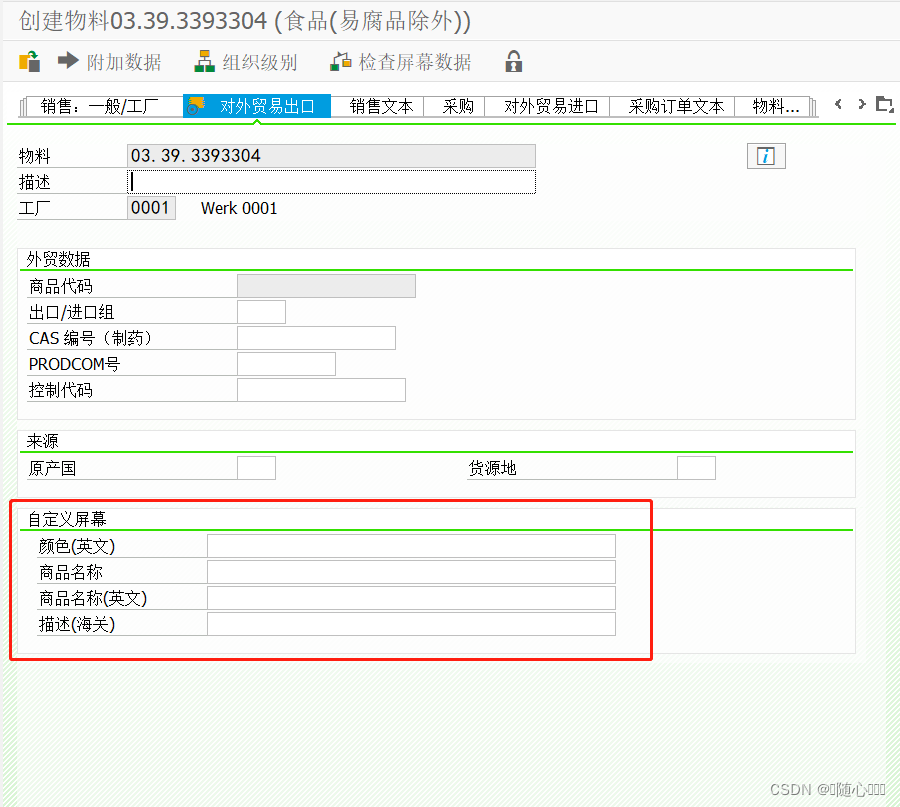
SAP 物料主数据屏幕增强
增强步骤 1.为主表添加一个附加结构 根据业务需求新建一个结构,结构中放入需要增强的屏幕字段并激活。 打开事务代码SE11,在需要保存的主表中添加这个附加结构并激活。 注:根据业务需求及屏幕增强的视图判断需要保存的主表是哪张ÿ…...

数据库-索引
介绍: 索引是帮助数据库高效获取数据的数据结构 优缺点: 优点:提高数据查询的效率,降低数据库的IO成本 通过索引列对数据进行排序,降低数据排序的成本,降低cpu消耗 缺点:索引会占用存储空间 索…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...
