双因素方差分析
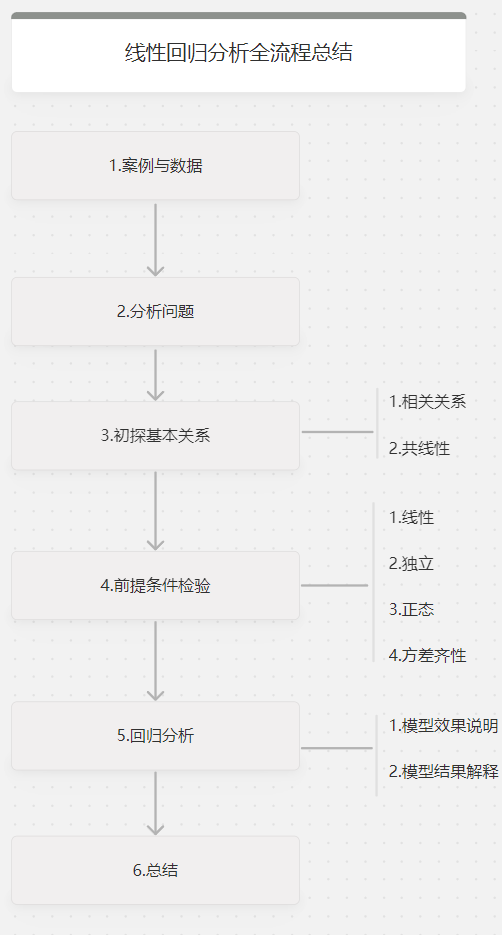
一、案例与数据
一家大型商业银行在多地区设有分行,其业务主要是进行基础设施建设,国家重点项目建设,固定资产投资等项目的贷款。近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提高,这给银行业务的发展带来较大压力。为弄清楚不良贷款形成的原因,管理者希望利用银行业务的有关数据做一些统计分析,想要知道“本年累积应收贷款”、 “贷款项目个数”以及“本年固定资产投资额”对“不良贷款”是否有影响,如果有影响,它们之间谁的影响更大?部分数据如下(数据虚构无实际意义):

二、分析问题
管理者想要研究“本年累积应收贷款”、 “贷款项目个数”以及“本年固定资产投资额”对“不良贷款”是否有影响,如果有影响,分析影响程度,其中以“不良贷款”作为因变量, “本年累积应收贷款”、 “贷款项目个数”以及“本年固定资产投资额”作为自变量研究影响关系,可以考虑线性回归、方差分析等,由于自变量和因变量均为定量变量,所以选择线性回归进行分析。
三、初探基本关系
在进行线性回归之前,首先需要对数据进行查看基本关系,然后进行检验数据是否满足参与线性回归分析的基本条件。基本关系包括数据的相关关系以及共线性的查看。
1.相关关系
在回归分析前一般需要做相关分析,因为有了相关关系,才可能有回归影响关系;如果没有相关关系,是不应该有回归影响关系的。所以进行初步查看,结果如下:

将“本年累计应收贷款”、“贷款项目个数”、“本年固定资产投资额”以及“不良贷款”之间进行两两相关分析。除了“本年固定资产投资额”和“不良贷款”之间p值大于0.05,其余两两之间分析p值均小于0.05,所以不良贷款与本年固定资产投资额没有相关关系,也即说明进行回归分析时不放入本年固定资产投资额。接下来查看数据是否存在共线性。
2.共线性
共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系(例如相关系数大于0.8)而使模型估计失真或难以估计准确。共线性的存在可能会降低估计的精准度,并且稳定性也会降低。无法判断单独变量的影响。回归方程的标准误差增大。变量显著性可能会失去意义等等。所以在分析前需要对共线性问题进行检查。

一般VIF值大于10(严格来说大于5),存在共线性问题,从分析结果中可以看到VIF值小于10,所以不存在共线性,如果存在共线性问题则不能使用线性回归,可以使用岭回归、Lasso回归等进行分析。
四、前提条件检验
大多数方法进行分析时,都有假设或者分析的前提条件,线性回归也不例外。线性回归分析的前提条件概括为四个:线性、独立、正态和方差齐性,接下来一一检验。
1.线性
一般检验数据之间的线性关系,是为了考察因变量随自变量值变化的情况,可以做相关分析从侧面进行说明或者利用散点图进行说明,散点图更加直观,所以本次选择散点图进行描述(SPSSAU可视化→散点图)。结果如下:

以“不良贷款(亿元)”作为Y轴,“本年累计应收贷款(亿元)”作为X轴建立散点图,发现“不良贷款(亿元)”与“本年累计应收贷款(亿元)”为线性关系。以同样的方法对“贷款项目个数”和“不良贷款”建立散点图,也存在线性关系。

如果不呈现线性关系可以尝试通过变量变换进行修正,常用的变量变换的方法有对数变换、倒数变换等等。
2.独立
独立是指残差是独立的。特别是,时间序列数据中的连续残差之间没有相关性。可以查看DW值,一般在DW值在2附近(比如1.7-2.3之间),则说明没有自相关性,模型构建良好,反之若DW值明显偏离2,则说明具有自相关性,模型构建较差(一般如果不是时间序列数据也可以不用过度关注)。尝试构建回归分析模型发现DW值为2.286。

从结果中可以看出DW值为2.286在2的附近,表示模型构建良好。接下来进行验证“正态”。
3.正态
正态表示残差服从正态分布。其方差σ2 = var (ei)反映了回归模型的精度,一般 σ 越小,用所得到回归模型预测y的精确度越高。建立回归分析模型得到残差与预测值,利用残差绘制直方图查看残差是否满足正态分布,结果如下:

如果直方图呈现‘中间高,两边低,左右基本对称的 “钟形图”则基本服从正态分析,但是数据量过少等也可能影响结果导致很难呈现出标准的正态分布,如果是这种情况如果看见‘钟形’也可以可以接受的。上图可以看出,数据呈现的分布并不对称,但是也出现近似‘钟形’曲线,所以也可以接受。残差满足正态分布,接下来验证方差齐性。
4.方差齐性
方差齐性是指残差的大小不随所有变量取值水平的改变而改变,即方差齐性。那么如何进行呢?首先对残差和预测值进行标准化,与标准化残差为Y轴,标准化预测值为X轴绘制散点图,如果所有点均匀分布在直线Y=0的两侧,则可以认为是方差齐性,结果如下:

从散点图可以发现数据大致均匀分布在Y=0的两侧,所以可认为是方差齐性,综上,数据满足回归分析的前提假设。可以进行线性回归。
五、回归分析
由上述分析与检验最后以“不良贷款(亿元)”为因变量,“本年累积应收贷款(亿元)”和“贷款项目个数(个)”为自变量构建线性回归模型。分析将从模型效果以及模型结果两部分进行说明。
1.模型效果说明
模型效果说明包括F检验以及模型拟合优度。
F检验

F检验主要是观测被解释变量的线性关系是否显著,上表可以看出,进行回归方程的显著性检验时,统计量F=17.521,对应的p值小于0.05,所以说明被解释变量的线性关系是显著的,可以建立模型。那么模型的拟合优度又是怎么样的?接下来进行说明。
拟合优度

模型拟合优度一般查看R方值(决定系数,模型拟合指标),如果R方为0.3代表自变量可以解释因变量30%的变化原因,一般越接近1说明拟合越好,但是很多研究中不会过多关注其大小,原因在于多数时候我们更在乎X对于Y是否有影响关系。从上表可以看出,模型R方值为0.614,调整R方为0.579。调整R方也是模型拟合指标。当x个数较多是调整R²比R²更为准确。
意味着“本年累积应收贷款(亿元)”和“贷款项目个数(个)”可以解释“不良贷款”61.4%变化原因。可见,模型拟合优度良好,说明被解释变量可以被模型大部分解释。接下来对模型结果进行解释。
2.模型结果解释
管理者想要知道“本年累积应收贷款”、 “贷款项目个数”以及“本年固定资产投资额”对“不良贷款”是否有影响,如果有影响,它们之间谁的影响更大?因为前面的相关分析中得到了“本年固定资产投资额”与“不良贷款”之间没有相关关系,一般情况下没有相关关系是没有影响关系的,所以分析“本年累积应收贷款”、 “贷款项目个数”对“不良贷款”的影响关系,模型结果分为“是否有影响”以及“影响程度”进行阐述。首先查看自变量对因变量是否有影响。
是否有影响

从上表可以看出,本年累计应收贷款分析项的t值为3.190,p值小于0.05说明此项具有显著性,即本年累计应收贷款对不良贷款有影响,贷款项目个数分析项的t值为2.126,p值小于0.05也说明此项具有显著性,即贷款项目个数对不良贷款有影响,二者对不良贷款有影响,具体谁影响大接下来进行说明。
影响程度
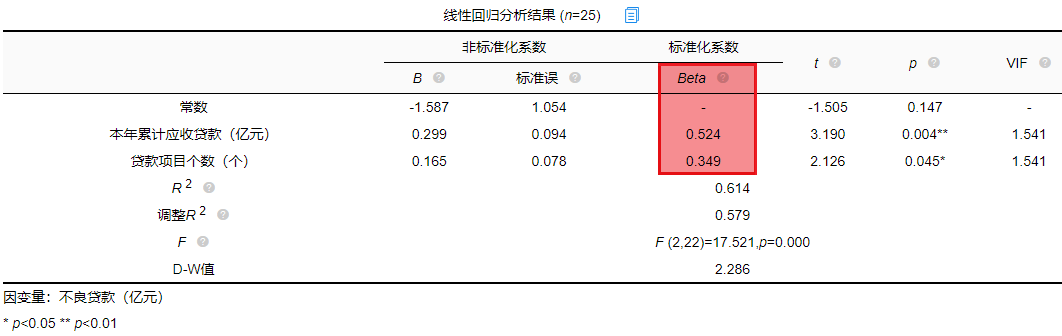
一般有影响关系才会去比较影响程度大小,影响程度大小需要查看标准化系数,标准化系数的绝对值越大表明自变量对因变量的反应越大,即影响程度越大,从上表中可以看出0.524>0.349,说明本年累积应收贷款相比较贷款项目个数对不良贷款影响更大。
除此之外,如果利用回归分析进行预测等,可以使用非标准化系数进行构建模型公式,具体不在赘述,可以进入SPSSAU官网进行查看。
六、总结
利用线性回归对管理者的问题进行分析,首先对数据的进本关系进行查看以及探索数据是否满足线性回归分析的条件,对数据处理后进行线性回归分析,发现“本年累积应收贷款”、 “贷款项目个数”对“不良贷款”有影响,并且查看标准化系数发现“本年累积应收贷款”影响程度更大,这对于管理者后续分析提供了有效信息。分析完毕。
相关文章:

双因素方差分析
一、案例与数据 一家大型商业银行在多地区设有分行,其业务主要是进行基础设施建设,国家重点项目建设,固定资产投资等项目的贷款。近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提高,这给银行…...

[ vulhub漏洞复现篇 ] Drupal XSS漏洞 (CVE-2019-6341)
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

「TCG 规范解读」第8章 TPM工作组 TPM 1.2中 SHA1的使用
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

熵权法计算权重
文章目录1. 多属性决策问题2. 熵(entropy)3. 信息熵4. 熵权法5. 熵权法的实现基于信息论的熵值法是根据各指标所含信息有序程度的差异性来确定指标权重的客观赋权方法,仅依赖于数据本身的离散程度。熵用于度量不确定性,指标的离散…...

redis实现用户签到,统计活跃用户,用户在线状态,用户留存率
开发的过程中,可能会遇到用户签到、统计当天的活跃用户、以及每个用户的在线状态,用户留存率的开发需求,可能会用传统的方法,根据相应的需求设计数据库表等,但这样耗费的存储空间大,以及性能方面也不会太好…...
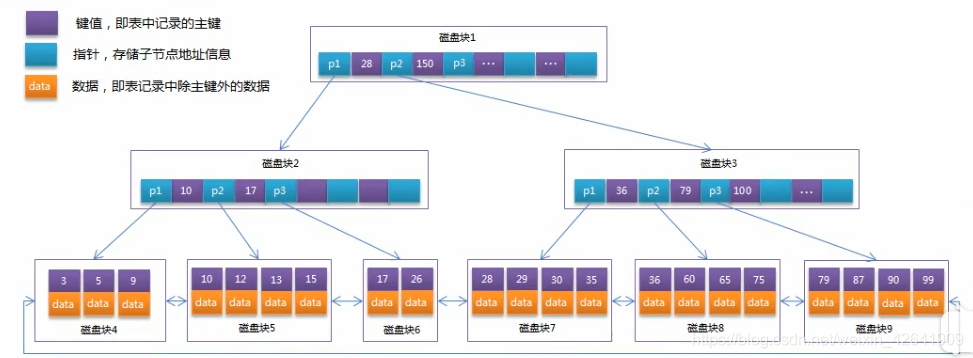
MySQL中有多少种索引?索引的底层实现原理
索引存储在内存中,为服务器存储引擎为了快速找到记录的一种数据结构。索引的主要作用是加快数据查找速度,提高数据库的性能。索引的分类(1) 普通索引:最基本的索引,它没有任何限制。(2) 唯一索引:与普通索引类似&#…...
以及线索二叉树java详解)
LeetCode经典算法题:二叉树遍历(递归遍历+迭代遍历+层序遍历)以及线索二叉树java详解
LeetCode经典算法题:二叉树遍历(递归遍历迭代遍历层序遍历)以及线索二叉树java详解 文章目录二叉树遍历题目描述解题思路与代码递归遍历迭代遍历层序遍历线索二叉树:二叉树遍历 题目描述 从根节点往下查找,先找左子树…...

【Java闭关修炼】MyBatis-接口代理的方式实现Dao层
【Java闭关修炼】MyBatis-接口代理的方式实现Dao层实现规则代码实现代理对象分析接口代理方式小结实现规则 映射配置文件中的名称空间必须和Dao层接口的全类名相同映射配置文件的增删改查标签的id属性必须和Dao层接口方法的参数相同映射配置文件中的增删改查标签的parameterTyp…...

2022年网络安全政策态势分析与2023年立法趋势
近日,公安部第三研究所网络安全法律研究中心与 360 集团法务中心联合共同发布了《全球网络安全政策法律发展年度报告(2022)》。《报告》概览2022年全球网络安全形势与政策法律态势,并对2023年及后续短期内网络安全政策、立法趋势进…...
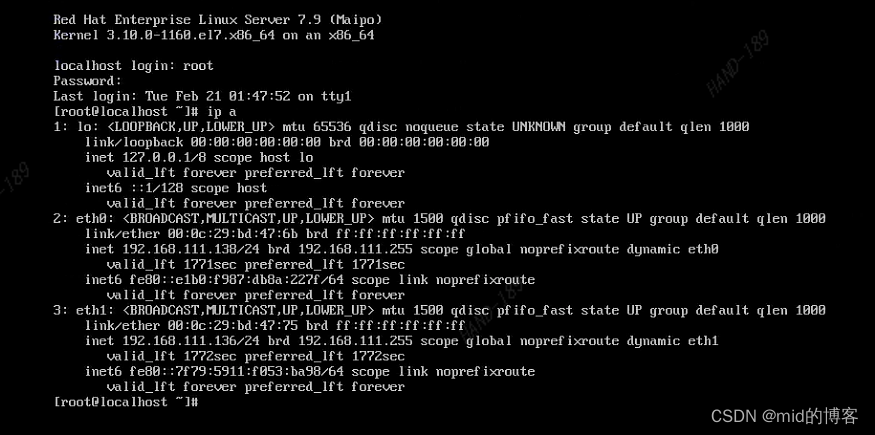
使用vmware制作云平台redhat7.9镜像模板
一、概述 1.1 redhat7.9 定制镜像上传到云平台。 这个制作镜像得方式适用于多种iso 镜像。 将iso 镜像通过vmware 创建出一台虚机,对虚机做一些基础配置。在虚机上安装kvm 虚拟化得工具, 将iso 镜像在导入虚机种通过kvm创建一下虚机, 虚机创…...

OpenCV基础(28)使用OpenCV进行摄像机标定Python和C++
摄像头是机器人、监控、太空探索、社交媒体、工业自动化甚至娱乐业等多个领域不可或缺的一部分。 对于许多应用,必须了解相机的参数才能有效地将其用作视觉传感器。 在这篇文章中,您将了解相机校准所涉及的步骤及其意义。 我们还共享 C 和 Python 代码以…...

APB总线详解及手撕代码
本文的参考资料为官方文档AMBA™3 APB Protocol specification文档下载地址: https://pan.baidu.com/s/1Vsj4RdyCLan6jE-quAsEuw?pwdw5bi 提取码:w5bi APB端口介绍介绍总线具体握手规则之前,需要先熟悉一下APB总线端口,APB的端口…...

【Linux/Windows】源文件乱码问题解决方法总结
🐚作者简介:花神庙码农(专注于Linux、WLAN、TCP/IP、Python等技术方向)🐳博客主页:花神庙码农 ,地址:https://blog.csdn.net/qxhgd🌐系列专栏:Linux技术&…...
Python 四大主流 Web 编程框架
目前Python的网络编程框架已经多达几十个,逐个学习它们显然不现实。但这些框架在系统架构和运行环境中有很多共通之处,本文带领读者学习基于Python网络框架开发的常用知识,及目前的4种主流Python网络框架:Django、Tornado、Flask、Twisted。 …...
学UI设计,可以向哪些方向发展?该怎么学?
1、什么是UI设计?UI设计,全称 User Interface,翻译成中文意思叫做用户界面设计。2、UI设计的类型UI设计按用户和界面来分可分成四种UI设计。分别是移动端UI设计,PC端UI设计,游戏UI设计,以及其它UI设计。第一…...
【C++】初识CC++内存管理
前言 我们都知道C&C是非常注重性能的语言,因此对于C&C的内存管理是每一个C/C学习者必须重点掌握的内容,本章我们并不是深入讲解C&C内存管理,而是介绍C&C内存管理的基础知识,为我们以后深入理解C&C内存管理做铺…...
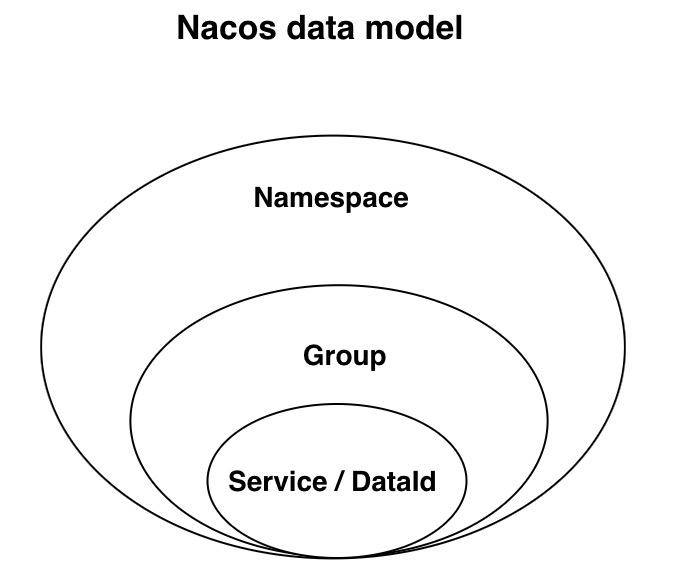
Nacos快速使用指南
简单例子:springboot快速集成nacos官方github文档命名空间是绝对隔离的。group之间可以通过配置实现跨 group访问配置中心Nacos config官方文档应用级别的默认配置文件名(dataId)dataId 的完整格式如下:${prefix}-${spring.profil…...
复旦发布国内首个类ChatGPT模型MOSS,和《流浪地球》有关?
昨晚,复旦大学自然语言处理实验室邱锡鹏教授团队发布国内首个类ChatGPT模型MOSS,现已发布至公开平台https://moss.fastnlp.top/ ,邀公众参与内测。 MOSS和ChatGPT一样,开发的过程也包括自然语言模型的基座训练、理解人类意图的对…...
国家级高新区企业主要经济指标(2012-2021年)
数据来源:国家统计局 时间跨度:2012-2021 区域范围:全国(及各分类统计指标) 指标说明:手工提取最新的中国统计年鉴数据中各个excel指标表,形成各个指标文件的多年度数据,便于多年…...
SpringBoot2核心技术-核心功能【05、Web开发】
目录 1、SpringMVC自动配置概览 2、简单功能分析 2.1、静态资源访问 1、静态资源目录 2、静态资源访问前缀 2.2、欢迎页支持 2.3、自定义 Favicon 2.4、静态资源配置原理 3、请求参数处理 0、请求映射 1、rest使用与原理 2、请求映射原理 1、普通参数与基本注解 …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
