GO远程构建并调试
GO远程调试
之前写C++,一直习惯了本地IDE+Remote CMake/GDB编译调试的模式。
因为6.824课程需要用GO,好像没有特别好的支持。记录一下如何配置调试的。
IDE: Goland
操作系统:Windows
远程服务器:Ubuntu
- 首先配置SSH,让其可以连接到服务器
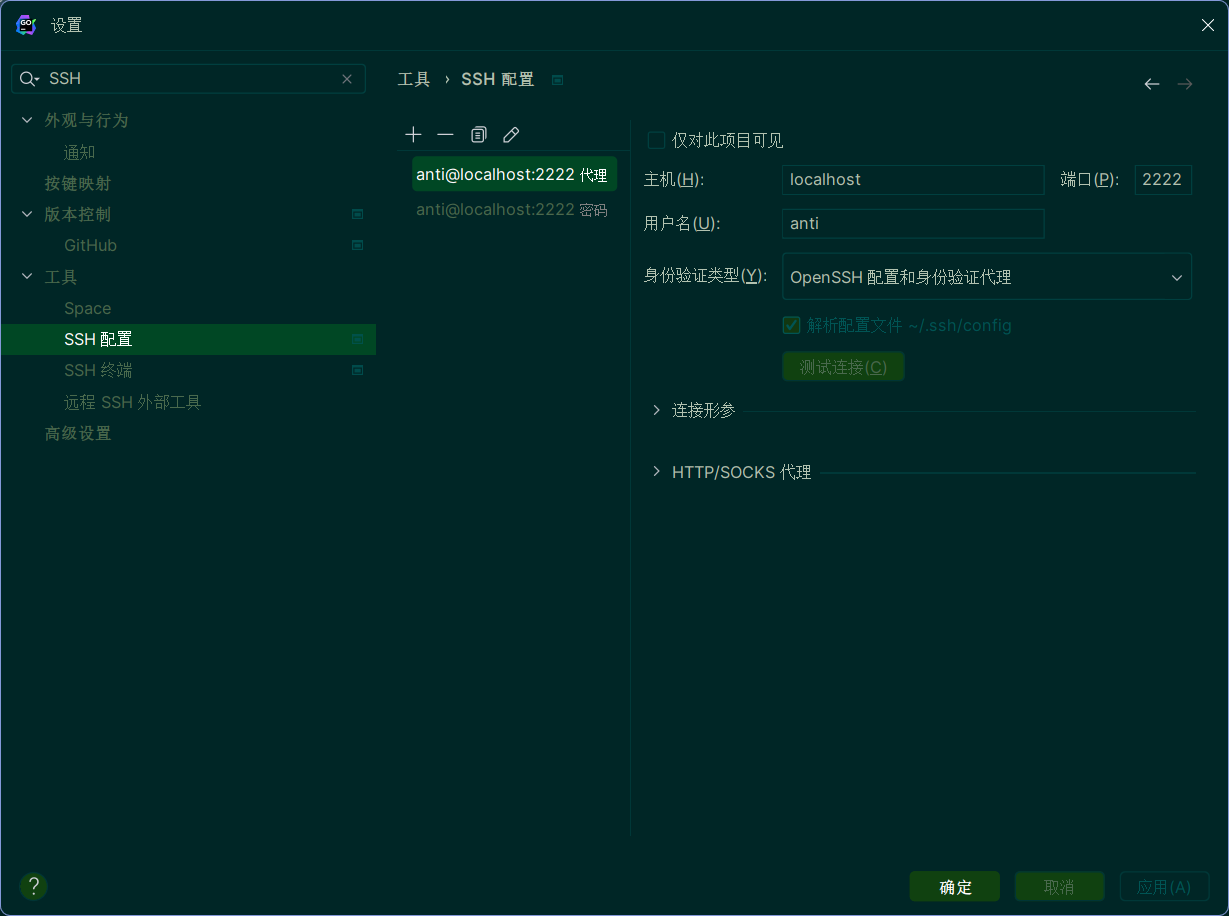
- 配置部署。选择SFTP。在映射中选择上传的路径。
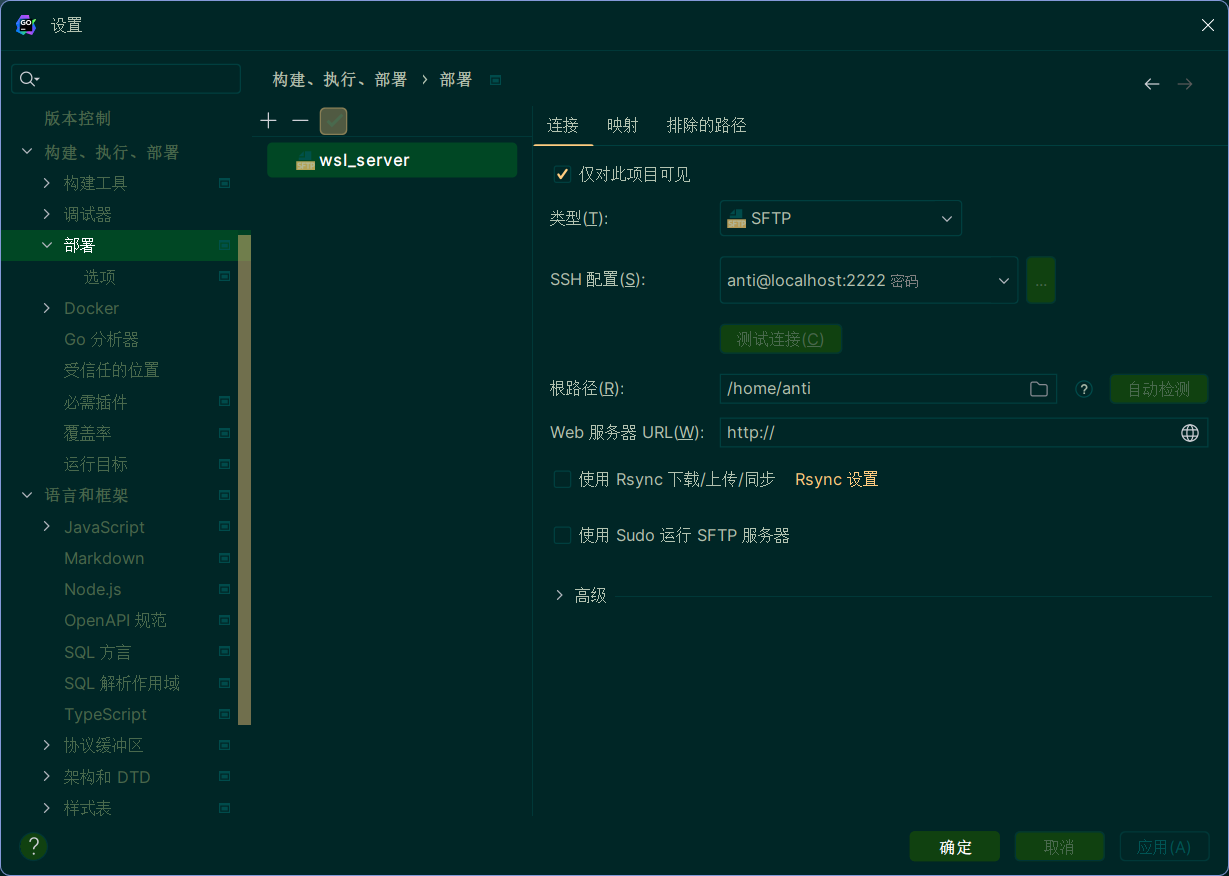
这样就实现了本地和服务器文件的同步
- 在服务器上安装delve
因为是ubuntu,我是直接sudo apt install delve就能进行安装。
但是后面发现直接这样安装的话版本有冲突
然后使用dlv version进行安装检查
使用源码进行安装:
cd ~git clone git@github.com:go-delve/delve.gitcd delvego install github.com/go-delve/delve/cmd/dlv
这个时候在你的go目录下,(比如我的是~/go/bin)会出现名字叫dlv的可执行文件。
然后将该路径添加到环境变量就行了。
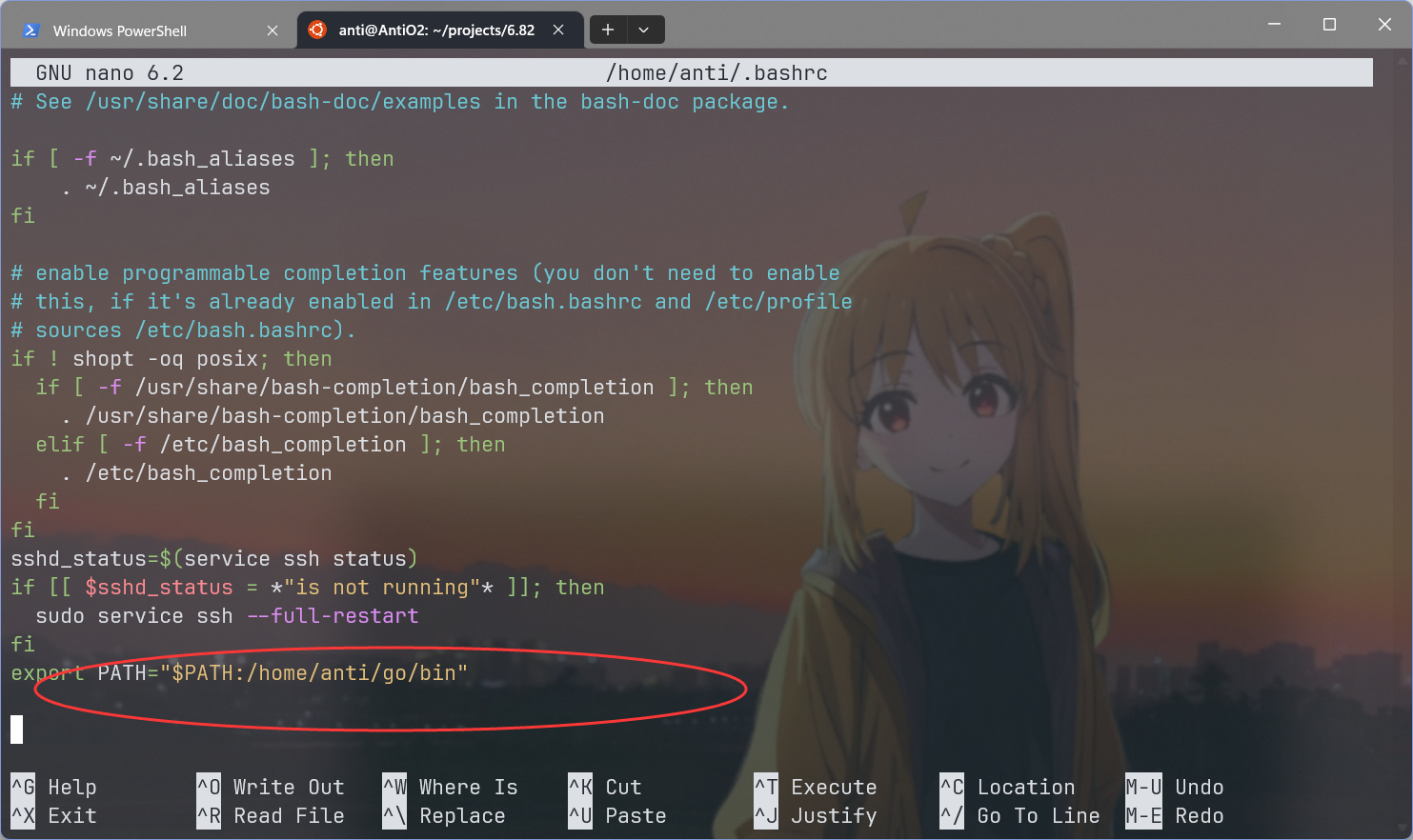
此时dlv version可以正确显示版本
dlv version
Delve Debugger
Version: 1.21.0
Build: $Id: fec0d226b2c2cce1567d5f59169660cf61dc1efe $
- 编写测试文件
package mainimport ("fmt""runtime"
)func main() {fmt.Println("Hello Go")showOS()
}func showOS() {os := runtime.GOOSfmt.Println("当前操作系统是:", os)
}
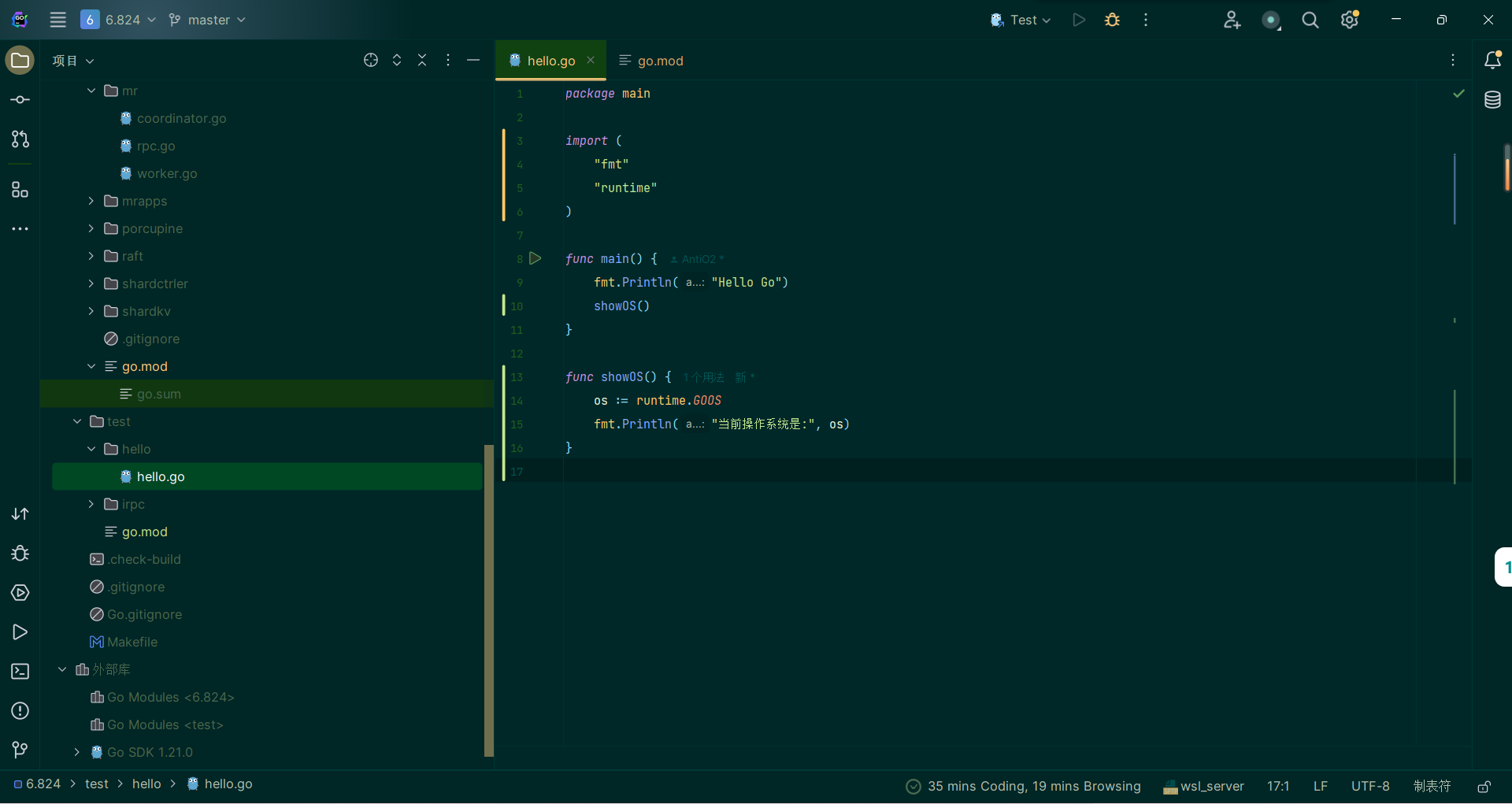
测试代码说明:创建目录test,并且创建go.mod文件。
- 配置Go Remote
然后使用终端进入你的服务器代码路径,比如我的是~/projects/6.824/test/hello。
按照提示运行
dlv debug --headless --listen=:2345 --api-version=2 --accept-multiclient
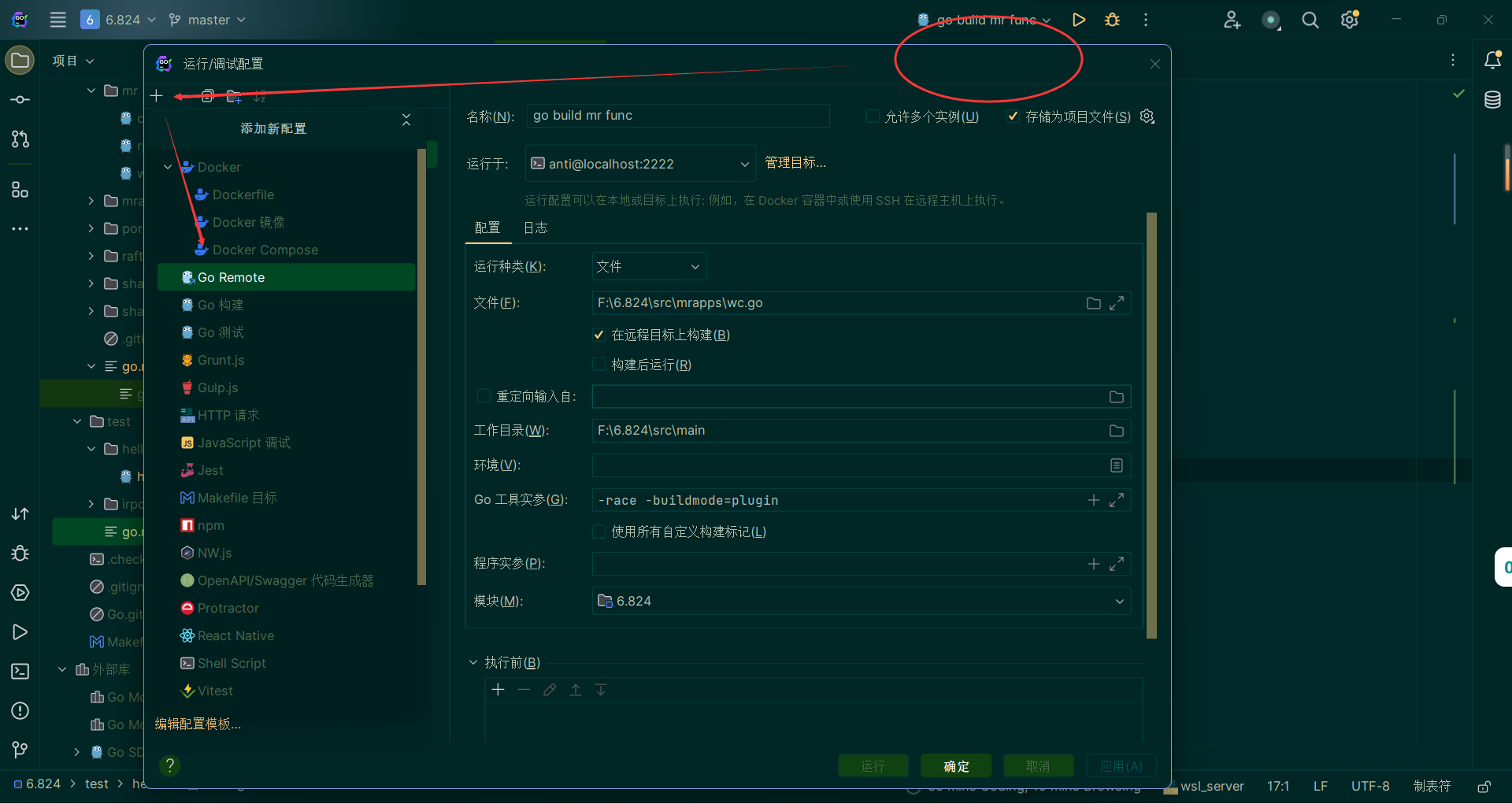
- 进行运行配置
这里运行于选择之前部署的服务器。然后在远程目标上构建
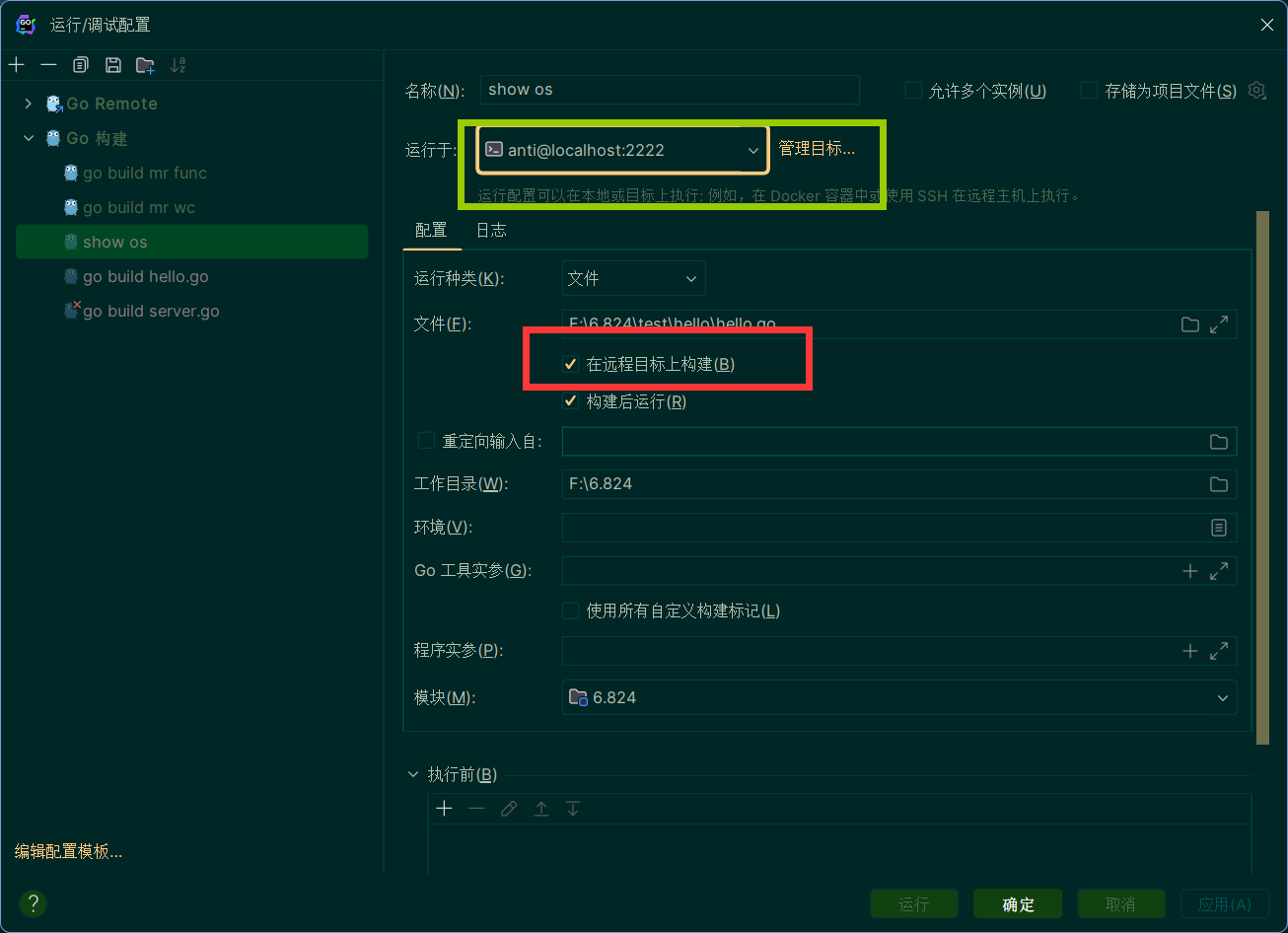
- 进行调试
可以看到,此时已经可以在服务器上构建并单步调试代码了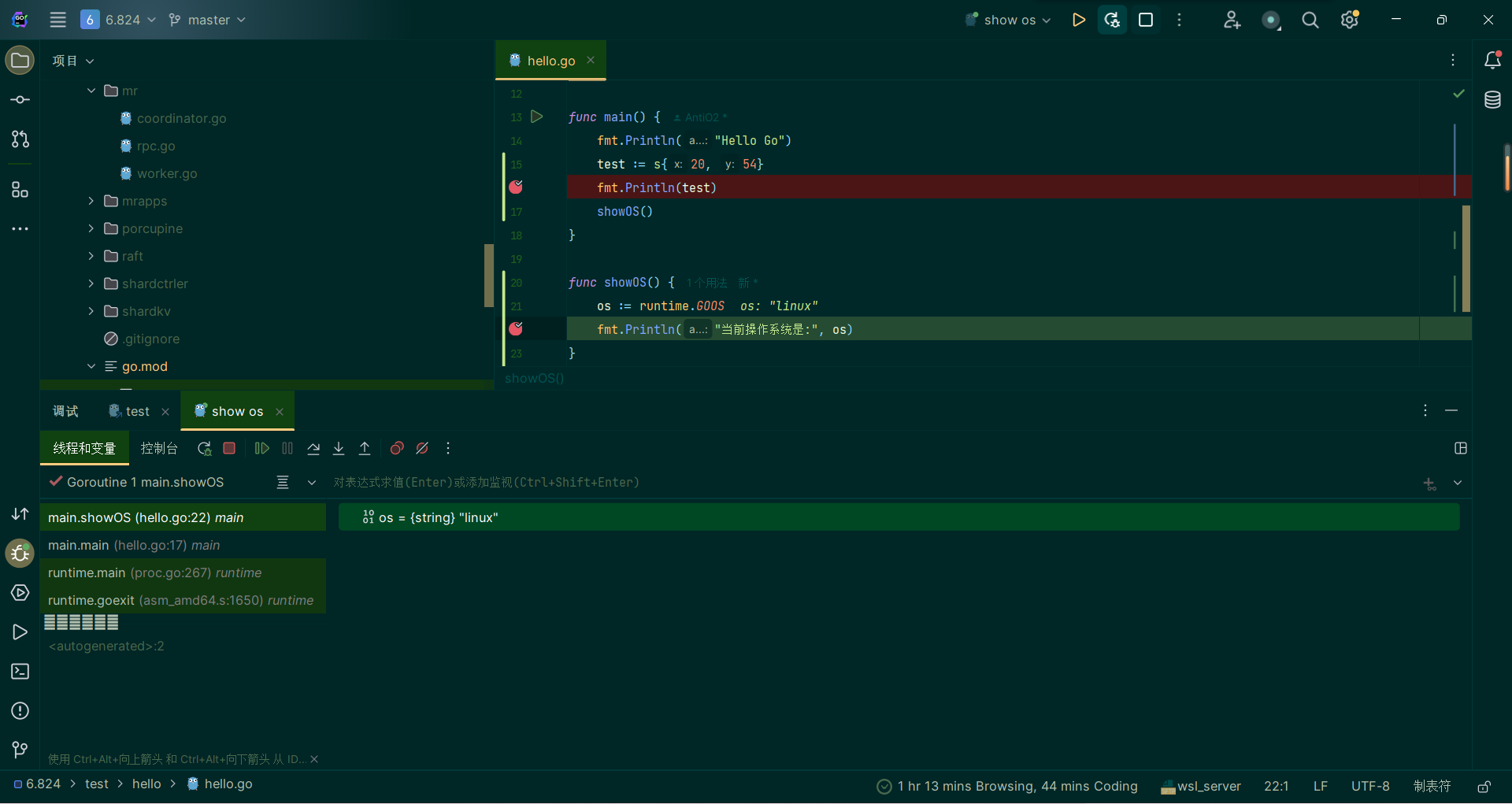
相关文章:

GO远程构建并调试
GO远程调试 之前写C,一直习惯了本地IDERemote CMake/GDB编译调试的模式。 因为6.824课程需要用GO,好像没有特别好的支持。记录一下如何配置调试的。 IDE: Goland 操作系统:Windows 远程服务器:Ubuntu 首先配置SSH,让其可以连接到…...
react使用hook封装一个search+input+checkbox组件
目录 react使用hook封装一个searchinputcheckbox组件searchPro.jsx使用组件效果 react使用hook封装一个searchinputcheckbox组件 searchPro.jsx import { Checkbox, Input } from "antd"; import React, { useEffect, useState } from "react"; import S…...

【6】uniform颜色写入
之前的Basic.shader: #shader vertex #version 330 corelayout(location 0) in vec4 position;void main() {gl_Position position; };#shader fragment #version 330 corelayout(location 0) out vec4 color;void main() {color vec4(1.0, 0.0, 0.0, 1.0); };这里color …...

自然语言处理历史史诗:NLP的范式演变与Python全实现
目录 一、引言什么是自然语言处理?语言与人类思维自然语言的复杂性NLP的历史轨迹 二、20世纪50年代末到60年代的初创期符号学派重要的研究和突破 随机学派重要的研究和突破 三、20世纪70年代到80年代的理性主义时代基于逻辑的范式重要的研究和突破 基于规则的范式重…...
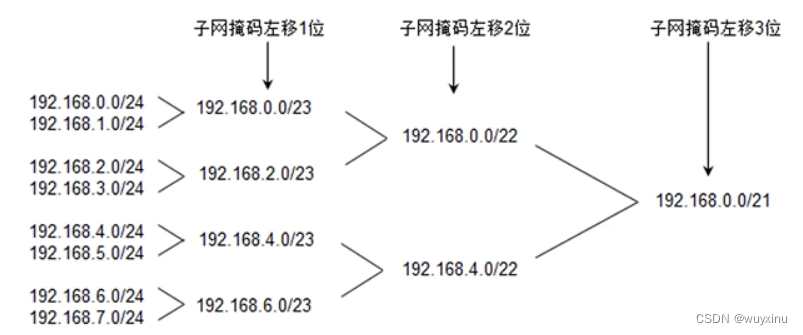
网络协议从入门到底层原理学习(二)—— Mac地址/IP地址
文章目录 网络协议从入门到底层原理学习(二)—— Mac地址/IP地址1、MAC地址2、MAC地址的表示格式3、MAC地址表4、MAC地址操作5、MAC地址的获取6、ARP7、ICMP8、IP地址9、IP地址的分类和格式10、不同分类的IP地址的范围11、特殊 IP 地址12、子网掩码13、子…...

2023开学礼中国海洋大学《乡村振兴战略下传统村落文化旅游设计》许少辉新海洋图书馆
2023开学礼中国海洋大学《乡村振兴战略下传统村落文化旅游设计》许少辉新海洋图书馆...

WebClient vs HttpClient:异同对比
在 Java 开发中,进行网络通信是常见的需求。WebClient 和 HttpClient 是两种常用的用于发送 HTTP 请求的工具。它们都具有相似的功能,但在实现细节和用法上存在一些差异。本文将详细介绍 WebClient 和 HttpClient 的异同,帮助您选择适合您项目…...

ES6中导入import导出export
ES6使用 export 和 import 来导出、导入模块 用法 /** 导出 export *///分别导出 export let name 孙悟空; export function sum(a, b) {return a b; } } //先定义再导出 let age 18 export {age}/** 默认导出 export default */const a 默认导出; export default a;/**…...
内外连接)
【MySQlL学习笔记】(九)内外连接
内外连接 内连接外连接左外连接右外连接 表的连接分为内连和外连 内连接 内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选,我们前面学习的查询都是内连接,也是在开发过程中使用的最多的连接查询。 语法: select 字段 from 表…...

敦煌https证书能做些什么
随着互联网技术的不断发展,人们的生活方式和社交方式也发生了巨大的变化。互联网已经成为人们生活中不可或缺的一部分,它不仅提供了方便快捷的信息获取方式,还为人们提供了一个全新的社交平台。 然而,随着互联网的不断发展&#x…...
React路由)
React笔记(六)React路由
一、React路由简介 React 官方并没有提供对应的路由插件,因此,我们需要下载第三方的路由插件 —— React Router DOM。 React Router 在 2021 年 11 月份的时候更新 v6 的版本。本次课就主要讲解V6版本 二、路由配置 1、下载路由 在项目根目录中&am…...
【算法系列篇】分治-归并
文章目录 前言什么是归并算法1. 排序数组1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 数组中逆序对2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 计算右侧小于当前元素的个数3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 翻转对4.1 题目要求4.2 做题思路4.3 Java代码实现 总…...
word导出为HTML格式教程,同时也导出图片
在写文档教程时,有时需要借鉴人家的专业文档内容,一般都是word格式文档。word直接复制里面的内容,帐帖到网站编辑器会有很多问题,需要二次清楚下格式才行,而且图片是没办法直接复制到编辑器内的。所以最方便的办法是将…...

事务的优化
例子: 举例:假设我们有一个文件上传的uploadFile方法,在这个方法中我们会先执行上传一个文件到分布式文件系统中的方法addMediaFilesToMinIO( ),上传成功后执行文件资源数据入库的addMediaFilesToDb( ),那么这个时候事务应该加在哪…...
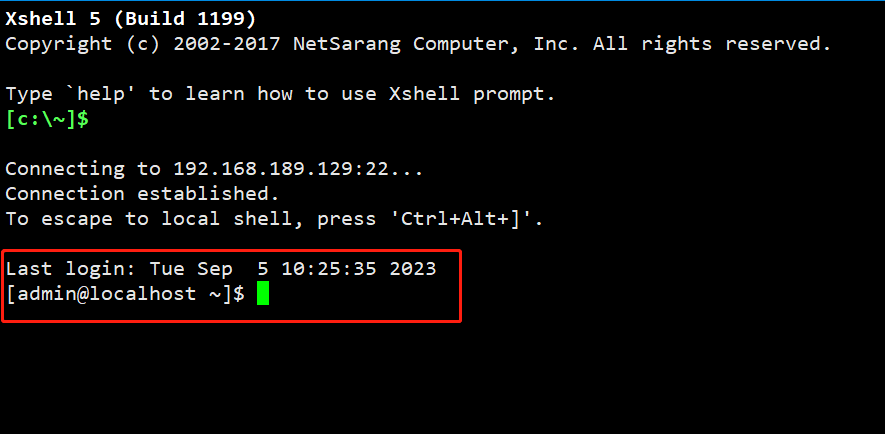
VMware虚拟机安装_新虚拟机创建_CentOS镜像导入_linux指令基本操作
文章目录 1 VMware下载安装1.1 下载网址1.2 安装步骤 2 创建虚拟机与CentOS镜像导入2.1 创建新虚拟机2.2 导入CentOS镜像 3 获取ip与连接Xshell3.1 查看虚拟机ip地址3.2 Xshell使用 1 VMware下载安装 1.1 下载网址 https://www.vmware.com/cn/products/workstation-pro/works…...
Git常用命令用法
参考视频:真的是全能保姆 git、github 保姆级教程入门,工作和协作必备技术,github提交pr - pull request_哔哩哔哩_bilibili 1.Git初始化 首先设置名称和邮箱。然后初始化一下,然后就创建了一个空的Git仓库。 PS D:\golang\oth…...

电子元器件采购的数字化转型:智能采购工具的应用
电子元器件采购的数字化转型是采购领域的一项重要趋势,智能采购工具的应用在此过程中发挥了关键作用。以下是智能采购工具在电子元器件采购数字化转型中的应用方面的一些关键点: 供应链可见性: 智能采购工具可以提供对供应链的实时可见性。通…...
【RuoYi移动端】uni-app中通过vuex的store来实现全局变量的修改和读取
一、在store文件中新建csjVar.js文件 const csjVar {csjMess: [{aaa:"ok"},{bbb:"no"}] } export default csjVar 二、修改store文件中新建index.js文件 import Vue from vue import Vuex from vuex import user from /store/modules/user import gette…...
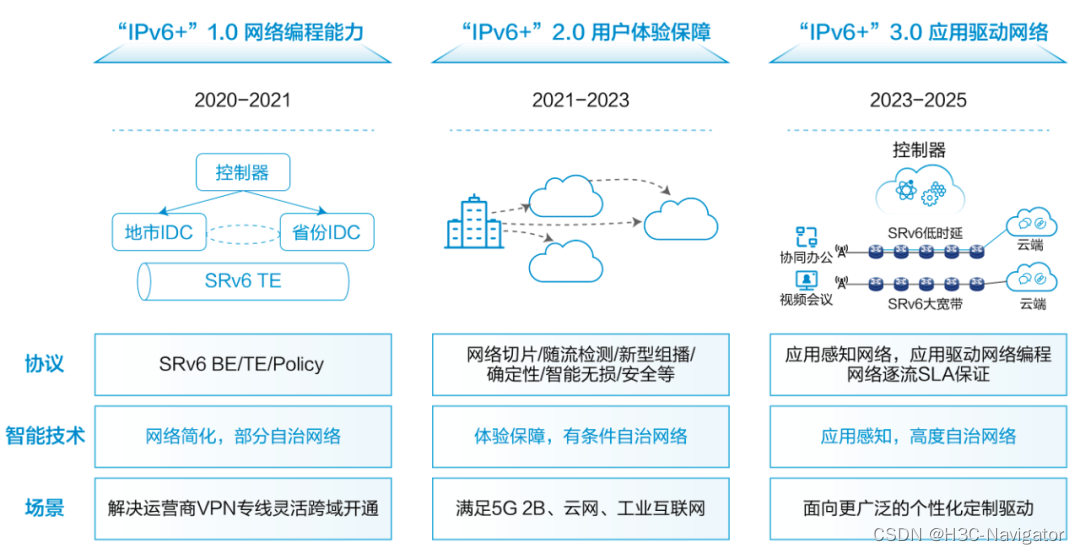
IPv6改造深化之路
01 IPv6改造问题及整体改造思路 随着“十四五”期间国家政策对IPv6深化改造及规模部署的推动,在IPv6改造过程中出现了越来越多的系统性问题,如图1所示。 图1 关于IPv6改造的各种疑问所有跨设备通信的IT软硬件系统均需要处理IP地址,各领域均需…...
,isdigit(),isspace(),round()源码)
atoi(),isdigit(),isspace(),round()源码
atoi()是一个C标准库函数,用于将字符串转换为对应的整数。 以下是atoi()函数的一种简化版本的示例实现: int atoi(const char* str) {int result 0;int sign 1;int i 0;// 处理空格while (isspace(str[i])) {i;}// 处理正负号if (str[i] - || str[…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
