LeetCode 338. Counting Bits【动态规划,位运算】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
提示:
0 <= n <= 10^5
进阶:
- 很容易就能实现时间复杂度为
O(n log n)的解决方案,你可以在线性时间复杂度O(n)内用一趟扫描解决此问题吗? - 你能不使用任何内置函数解决此问题吗?(如,C++ 中的
__builtin_popcount)
这道题需要计算从 0 0 0 到 n n n 的每个整数的二进制表示中的 1 1 1 的数目。
部分编程语言有相应的内置函数用于计算给定的整数的二进制表示中的 1 1 1 的数目,例如 Java 的 Integer.bitCount ,C++ 的 __builtin_popcount 。下列各种方法均为不使用内置函数的解法。
为了表述简洁,下文用「一比特数」表示二进制表示中的 1 1 1 的数目。
解法1 B r i a n K e r n i g h a n Brian Kernighan BrianKernighan 算法
最直观的做法是对从 0 0 0 到 n n n 的每个整数直接计算「一比特数」。每个int型的数都可以用 32 32 32 位二进制数表示,只要遍历其二进制表示的每一位即可得到 1 1 1 的数目。
利用 Brian Kernighan 算法,可以在一定程度上进一步提升计算速度。该算法的原理是:对于任意整数 x x x ,令 x = x & ( x − 1 ) x=x~\&~(x-1) x=x & (x−1) ,该运算将 x x x 的二进制表示的最后一个 1 1 1 变成 0 0 0 。因此,对 x x x 重复该操作,直到 x x x 变成 0 0 0 ,则操作次数即为 x x x 的「一比特数」。
对于给定的 n n n,计算从 0 0 0 到 n n n 的每个整数的「一比特数」的时间都不会超过 O ( log n ) O(\log n) O(logn) ,因此总时间复杂度为 O ( n log n ) O(n \log n) O(nlogn) 。
class Solution {public int[] countBits(int n) {int[] bits = new int[n + 1];for (int i = 0; i <= n; i++) bits[i] = countOnes(i);return bits;}public int countOnes(int x) {int ones = 0;while (x > 0) {x &= (x - 1);ones++;}return ones;}
}
复杂度分析:
- 时间复杂度: O ( n log n ) O(n \log n) O(nlogn) 。需要对从 0 0 0 到 n n n 的每个整数使用计算「一比特数」,对于每个整数计算「一比特数」的时间都不会超过 O ( log n ) O(\log n) O(logn) 。
- 空间复杂度: O ( 1 ) O(1) O(1) 。除了返回的数组以外,空间复杂度为常数。
解法2 动态规划——最高有效位
方法一需要对每个整数使用 O ( log n ) O(\log n) O(logn) 的时间计算「一比特数」。可以换一个思路,当计算 i i i 的「一比特数」时,如果存在 0 ≤ j < i 0 \le j<i 0≤j<i , j j j 的「一比特数」已知,且 i i i 和 j j j 相比, i i i 的二进制表示只多了一个 1 1 1 ,则可以快速得到 i i i 的「一比特数」。令 bits [ i ] \textit{bits}[i] bits[i] 表示 i i i 的「一比特数」,则上述关系可以表示成: bits [ i ] = bits [ j ] + 1 \textit{bits}[i]= \textit{bits}[j]+1 bits[i]=bits[j]+1 。
对于正整数 x x x ,如果可以知道最大的正整数 y y y ,使得 y ≤ x y \le x y≤x 且 y y y 是 2 2 2 的整数次幂,则 y y y 的二进制表示中只有最高位是 1 1 1 ,其余都是 0 0 0,此时称 y y y 为 x x x 的「最高有效位」。令 z = x − y z=x-y z=x−y ,显然 0 ≤ z < x 0 \le z<x 0≤z<x ,则 bits [ x ] = bits [ z ] + 1 \textit{bits}[x]=\textit{bits}[z]+1 bits[x]=bits[z]+1 。
为了判断一个正整数是不是 2 2 2 的整数次幂,可以利用方法一中提到的按位与运算的性质。如果正整数 y y y 是 2 2 2 的整数次幂,则 y y y 的二进制表示中只有最高位是 1 1 1,其余都是 0 0 0,因此 y & ( y − 1 ) = 0 y~\&~(y-1) = 0 y & (y−1)=0 。由此可见,正整数 y y y 是 2 2 2 的整数次幂,当且仅当 y & ( y − 1 ) = 0 y~\&~(y-1)=0 y & (y−1)=0 。
显然, 0 0 0 的「一比特数」为 0 0 0 。使用 highBit \textit{highBit} highBit 表示当前的最高有效位,遍历从 1 1 1 到 n n n 的每个正整数 i i i,进行如下操作。
- 如果 i & ( i − 1 ) = 0 i~\&~(i-1)=0 i & (i−1)=0 ,则令 highBit = i \textit{highBit}=i highBit=i ,更新当前的最高有效位。
- i i i 比 i − highBit i-\textit{highBit} i−highBit 的「一比特数」多 1 1 1 ,由于是从小到大遍历每个整数,因此遍历到 i i i 时, i − highBit i-\textit{highBit} i−highBit 的「一比特数」已知,令 bits [ i ] = bits [ i − highBit ] + 1 \textit{bits}[i]=\textit{bits}[i-\textit{highBit}]+1 bits[i]=bits[i−highBit]+1 。
- 最终得到的数组 bits \textit{bits} bits 即为答案。
class Solution {public int[] countBits(int n) {int[] bits = new int[n + 1];int highBit = 0;for (int i = 1; i <= n; i++) {if ((i & (i - 1)) == 0) highBit = i;bits[i] = bits[i - highBit] + 1;}return bits;}
}
复杂度分析
- 时间复杂度: O ( n ) O(n) O(n) 。对于每个整数,只需要 O ( 1 ) O(1) O(1) 的时间计算「一比特数」。
- 空间复杂度: O ( 1 ) O(1) O(1) 。除了返回的数组以外,空间复杂度为常数。
解法3 动态规划——最低有效位
方法二需要实时维护最高有效位,当遍历到的数是 2 2 2 的整数次幂时,需要更新最高有效位。如果再换一个思路,可以使用「最低有效位」计算「一比特数」。
对于正整数 x x x ,将其二进制表示右移一位,等价于将其二进制表示的最低位去掉,得到的数是 ⌊ x 2 ⌋ \lfloor \frac{x}{2} \rfloor ⌊2x⌋ 。如果 bits [ ⌊ x 2 ⌋ ] \textit{bits}\big[\lfloor \frac{x}{2} \rfloor\big] bits[⌊2x⌋] 的值已知,则可以得到 bits [ x ] \textit{bits}[x] bits[x] 的值:
- 如果 x x x 是偶数,则 bits [ x ] = bits [ ⌊ x 2 ⌋ ] \textit{bits}[x]=\textit{bits}\big[\lfloor \frac{x}{2} \rfloor\big] bits[x]=bits[⌊2x⌋]
- 如果 x x x 是奇数,则 bits [ x ] = bits [ ⌊ x 2 ⌋ ] + 1 \textit{bits}[x]=\textit{bits}\big[\lfloor \frac{x}{2} \rfloor\big]+1 bits[x]=bits[⌊2x⌋]+1
上述两种情况可以合并成: bits [ x ] \textit{bits}[x] bits[x] 的值等于 bits [ ⌊ x 2 ⌋ ] \textit{bits}\big[\lfloor \frac{x}{2} \rfloor\big] bits[⌊2x⌋] 的值加上 x x x 除以 2 2 2 的余数。
由于 ⌊ x 2 ⌋ \lfloor \frac{x}{2} \rfloor ⌊2x⌋ 可以通过 x > > 1 x >> 1 x>>1 得到, x x x 除以 2 2 2 的余数可以通过 x & 1 x~\&~1 x & 1 得到,因此有: bits [ x ] = bits [ x > > 1 ] + ( x & 1 ) \textit{bits}[x]=\textit{bits}[x>>1]+(x~\&~1) bits[x]=bits[x>>1]+(x & 1)
遍历从 1 1 1 到 n n n 的每个正整数 i i i ,计算 bits \textit{bits} bits 的值。最终得到的数组 bits \textit{bits} bits 即为答案。
class Solution {public int[] countBits(int n) {int[] bits = new int[n + 1];for (int i = 1; i <= n; i++)bits[i] = bits[i >> 1] + (i & 1);return bits;}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 。对于每个整数,只需要 O ( 1 ) O(1) O(1) 的时间计算「一比特数」。
- 空间复杂度: O ( 1 ) O(1) O(1) 。除了返回的数组以外,空间复杂度为常数。
解法4 动态规划——最低设置位
定义正整数 x x x 的「最低设置位」为 x x x 的二进制表示中的最低的 1 1 1 所在位。例如, 10 10 10 的二进制表示是 101 0 ( 2 ) 1010_{(2)} 1010(2) ,其最低设置位为 2 2 2 ,对应的二进制表示是 1 0 ( 2 ) 10_{(2)} 10(2) 。
令 y = x & ( x − 1 ) y=x~\&~(x-1) y=x & (x−1) ,则 y y y 为将 x x x 的最低设置位从 1 1 1 变成 0 0 0 之后的数,显然 0 ≤ y < x 0 \le y<x 0≤y<x , bits [ x ] = bits [ y ] + 1 \textit{bits}[x]=\textit{bits}[y]+1 bits[x]=bits[y]+1 。因此对任意正整数 x x x ,都有 bits [ x ] = bits [ x & ( x − 1 ) ] + 1 \textit{bits}[x]=\textit{bits}[x~\&~(x-1)]+1 bits[x]=bits[x & (x−1)]+1 。
遍历从 1 1 1 到 n n n 的每个正整数 i i i,计算 bits \textit{bits} bits 的值。最终得到的数组 bits \textit{bits} bits 即为答案。
class Solution {public int[] countBits(int n) {int[] bits = new int[n + 1];for (int i = 1; i <= n; i++)bits[i] = bits[i & (i - 1)] + 1;return bits;}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 。对于每个整数,只需要 O ( 1 ) O(1) O(1) 的时间计算「一比特数」。
- 空间复杂度: O ( 1 ) O(1) O(1) 。除了返回的数组以外,空间复杂度为常数。
相关文章:

LeetCode 338. Counting Bits【动态规划,位运算】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

解释 Git 的基本概念和使用方式。
Git 是一种分布式版本控制系统,它可以跟踪文件的修改历史、协调多个人员的工作、将分支合并到一起等。下面是 Git 的一些基本概念和使用方式。 - 仓库(Repository):存储代码、版本控制历史记录等的地方。 - 分支(Bran…...
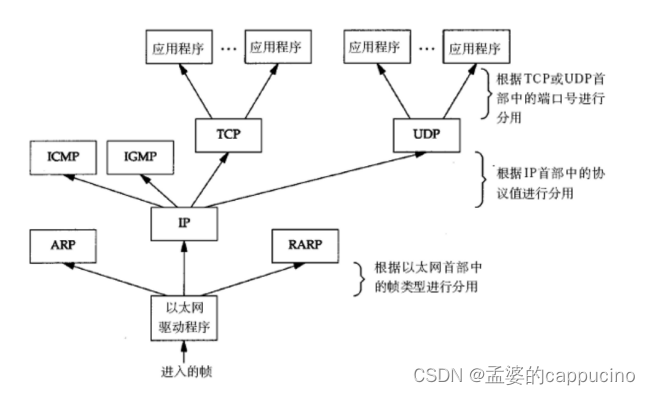
计算机网络初识
目录 1、计算机网络背景 网络发展 认识 "协议" 2、网络协议初识 OSI七层模型 TCP/IP五层(或四层)模型 3、网络传输基本流程 网络传输流程图 数据包封装和分用 4、网络中的地址管理 认识IP地址 认识MAC地址 1、计算机网络背景 网络发展 在之前呢&…...

python 笔记(2)——文件、异常、面向对象、装饰器、json
目录 1、文件操作 1-1)打开文件的两种方式: 1-2)文件操作的简单示例: write方法: read方法: readline方法: readlines方法: 2、异常处理 2-1)不会中断程序的异常捕获和处理…...
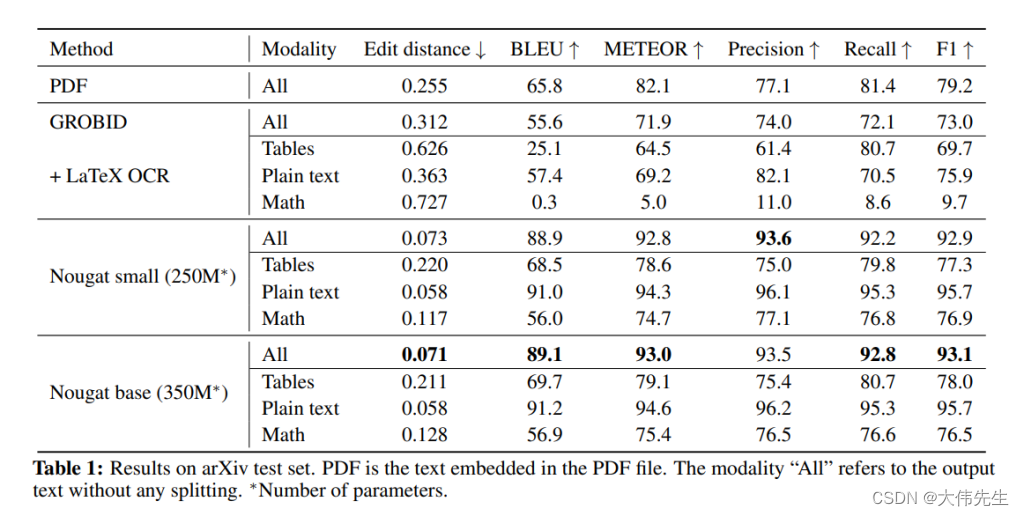
Meta AI的Nougat能够将数学表达式从PDF文件转换为机器可读文本
大多数科学知识通常以可移植文档格式(PDF)的形式存储,这也是互联网上第二突出的数据格式。然而,从这种格式中提取信息或将其转换为机器可读的文本具有挑战性,尤其是在涉及数学表达式时。 为了解决这个问题,…...

【Python爬虫笔记】爬虫代理IP与访问控制
一、前言 在进行网络爬虫的开发过程中,有许多限制因素阻碍着爬虫程序的正常运行,其中最主要的一点就是反爬虫机制。为了防止爬虫程序在短时间内大量地请求同一个网站,网站管理者会使用一些方式进行限制。这时候,代理IP就是解决方…...

50、Spring WebFlux 的 自动配置 的一些介绍,与 Spring MVC 的一些对比
Spring WebFlux Spring WebFlux 简称 WebFlux ,是 spring5.0 新引入的一个框架。 SpringBoot 同样为 WebFlux 提供了自动配置。 Spring WebFlux 和 Spring MVC 是属于竞争关系,都是框架。在一个项目中两个也可以同时存在。 SpringMVC 是基于 Servlet A…...
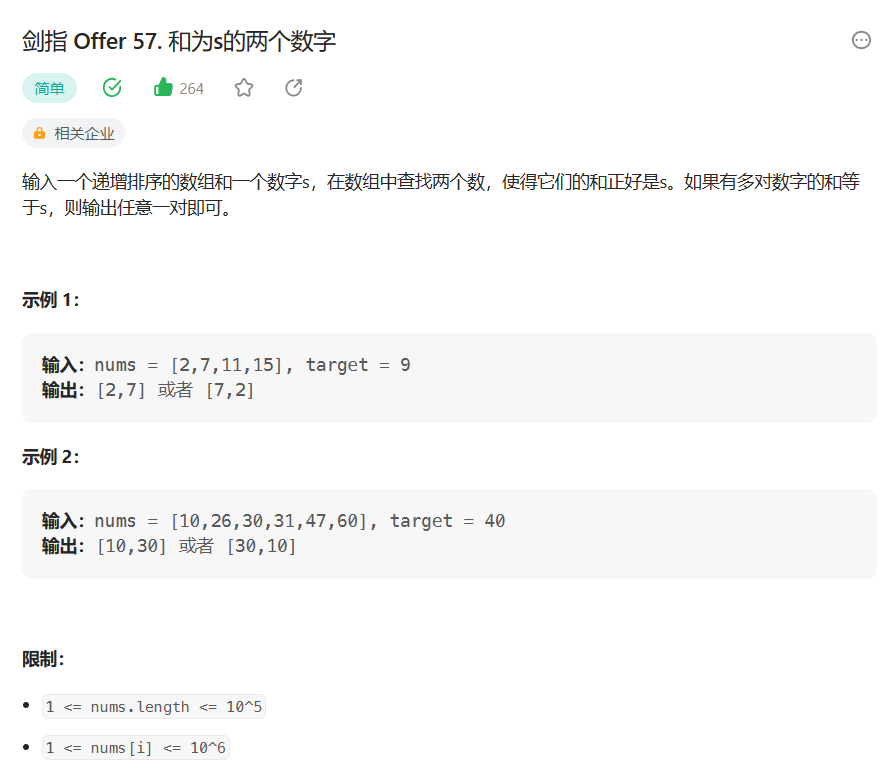
【算法专题突破】双指针 - 和为s的两个数字(6)
目录 1. 题目解析 2. 算法原理 3. 代码编写 写在最后: 1. 题目解析 题目链接:剑指 Offer 57. 和为s的两个数字 - 力扣(Leetcode) 这道题题目就一句话但是也是有信息可以提取的, 最重要的就是开始的那句话&#…...
Redis7入门概述
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Java从入门到精通 ✨特色专栏…...

SQL sever命名规范
目录 一、标识符 二、表名(Table): 三、字段名(fields): 四、约束(Constraint): 五、索引(Index): 六、存储过程(Stored Proced…...
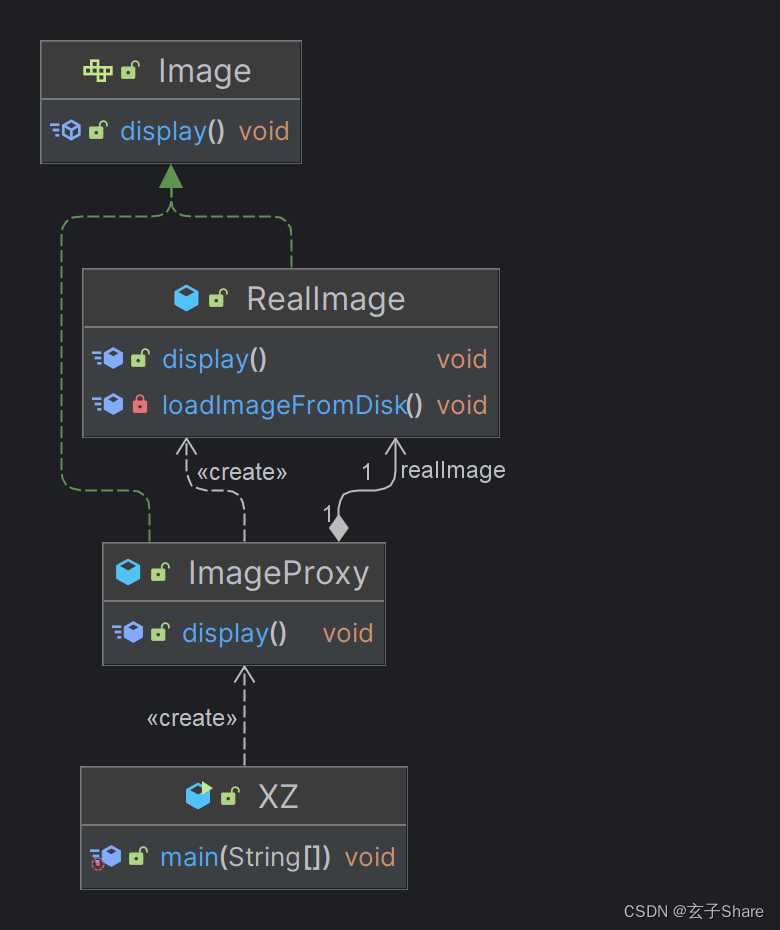
BCSP-玄子Share-Java框基础_工厂模式/代理模式
三、设计模式 3.1 设计模式简介 软件设计中的三十六计是人们在长期的软件开发中的经验总结是对某些特定问题的经过实践检验的特定解决方法被广泛运用在 Java 框架技术中 3.1.1 设计模式的优点 设计模式是可复用的面向对象软件的基础可以更加简单方便地复用成功的设计和体系…...

【数据结构】2015统考真题 6
题目描述 【2015统考真题】求下面的带权图的最小(代价)生成树时,可能是Kruskal算法第2次选中但不是Prim算法(从v4开始)第2次选中的边是(C) A. (V1, V3) B. (V1, V4) C. (V2, V3) D. (V3, V4) …...

HTML <track> 标签
实例 播放带有字幕的视频: <video width="320" height="240" controls="controls"><source src="forrest_gump.mp4" type="video/mp4" /><source src="forrest_gump.ogg" type="video/ogg…...

php中识别url被篡改并阻止访问的实现方式是什么
在 PHP 中,可以通过多种方式来识别并阻止 URL 被篡改的访问。以下是一些常见的方法: 基本身份验证:使用 PHP 的 $_SERVER[PHP_AUTH_USER] 和 $_SERVER[PHP_AUTH_PW] 变量可以实施基本的 HTTP 身份验证。在访问受保护的页面之前,可…...

c++ 学习 之 const,constexpr,volatile
前言 const、constexpr 和 volatile 是 C 中用于修饰变量和类型的关键字 正文 它们分别用于不同的用途: const(常量): const 用于声明常量,表示变量的值不能被修改。 它可以应用于变量、指针、引用、成员函数以及类…...

【Flink】关于jvm元空间溢出,mysql binlog冲突的问题解决
问题一:7张表是同一个mysql中的,我们进行增量同步时分别用不同的flink任务读取,造成mysql server-id冲突问题,如下: Caused by: io.debezium.DebeziumException: A slave with the same server_uuid/server_id as this…...
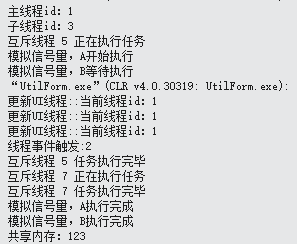
C#常用多线程(线程同步,事件触发,信号量,互斥锁,共享内存,消息队列)
using System; using System.Threading; using System.Windows.Forms; using UtilForm.Util;namespace UtilForm {// 线程同步,事件触发,信号量,互斥锁,共享内存,消息队列public partial class frmUIThread : Form{ Sy…...

OpenWrt系统开发笔记
openWrt英文官网: https://openwrt.org/ 中文官网: http://www.openwrt.org.cn/ 一、开发环境及编译 在github上有两个源码使用的比较多 一个是lede,地址为:https://github.com/coolsnowwolf/lede 另一个为OpenWrt的官方源码&#…...
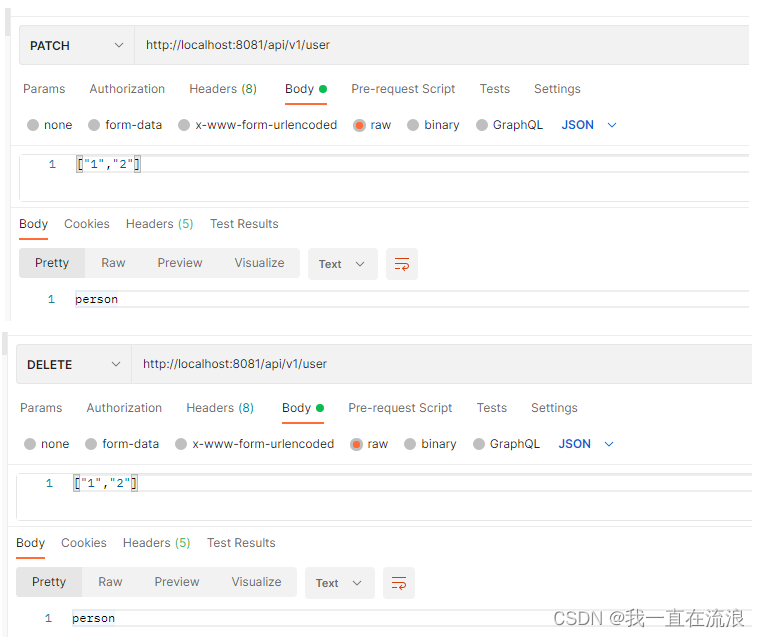
实战 - Restful APi 格式规范
文章目录 1. 特征2. 优点3. 动作1. GET 获取资源2. POST 创建资源3. PUT 整体替换4. PATCH 部分替换5. DELETE 删除资源 4. 示例 RESTful是一种API的设计风格,他和GraphQL ,JSON-RPC,WebService类似,用于定义在CS、BS架构下暴露服…...

《Linux从练气到飞升》No.21 Linux简单实现一个shell
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
