实践和项目:解决实际问题时,选择合适的数据结构和算法
文章目录
- 选择合适的数据结构
- 数组
- 链表
- 栈
- 队列
- 树
- 图
- 哈希表
- 选择合适的算法
- 实践和项目

🎉欢迎来到数据结构学习专栏~实践和项目:解决实际问题时,选择合适的数据结构和算法
- ☆* o(≧▽≦)o *☆嗨~我是IT·陈寒🍹
- ✨博客主页:IT·陈寒的博客
- 🎈该系列文章专栏:数据结构学习
- 📜其他专栏:Java学习路线 Java面试技巧 Java实战项目 AIGC人工智能 数据结构学习
- 🍹文章作者技术和水平有限,如果文中出现错误,希望大家能指正🙏
- 📜 欢迎大家关注! ❤️
在计算机科学中,数据结构和算法是两个非常重要的概念。数据结构是用来存储和组织数据的方式,而算法则是解决特定问题的步骤和操作。在实际应用中,选择合适的数据结构和算法对于提高程序的效率和解决实际问题的能力至关重要。

选择合适的数据结构
在计算机科学中,数据结构和算法是两个非常重要的概念。数据结构是用来存储和组织数据的方式,而算法则是解决特定问题的步骤和操作。在实际应用中,选择合适的数据结构和算法对于提高程序的效率和解决实际问题的能力至关重要。
数据结构的选择取决于具体的问题和场景。以下是一些常见的情况和对应的数据结构:

数组
数组是一种线性数据结构,它存储连续的元素,并可以通过索引直接访问。由于数组在内存中是连续存储的,因此访问数组元素的速度非常快。当需要快速访问元素时,数组是一种非常合适的数据结构。
下面是一个使用数组的示例代码片段:
# 创建一个包含10个整数的数组
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]# 访问数组中的元素
print(arr[0]) # 输出:1
print(arr[5]) # 输出:6
链表
链表是一种非连续的数据结构,它由一系列节点组成,每个节点包含一个指向下一个节点的指针。链表适用于需要动态分配内存的情况,因为可以在运行时动态地添加或删除节点。

下面是一个使用链表的示例代码片段:
public class Node {int value;Node next;public Node(int value) {this.value = value;this.next = null;}
}public class LinkedList {private Node head;public void add(int value) {Node newNode = new Node(value);if (head == null) {head = newNode;} else {Node current = head;while (current.next != null) {current = current.next;}current.next = newNode;}}public void remove(int value) {if (head == null) {return;}if (head.value == value) {head = head.next;return;}Node current = head;while (current.next != null && current.next.value != value) {current = current.next;}if (current.next != null) {current.next = current.next.next;}}
}
栈
栈是一种后入先出(FILO)的数据结构。它遵循“先进后出”(LIFO)的原则,即最后一个插入的元素是第一个被删除的元素。栈适用于需要先入后出(FILO)的数据处理。例如,后入先出的队列就可以用栈来实现。

下面是一个使用栈的示例代码片段:
stack = []
stack.append(1) # 插入元素1
stack.append(2) # 插入元素2
print(stack.pop()) # 删除并返回元素2,输出:2
print(stack.pop()) # 删除并返回元素1,输出:1
队列
队列是一种先入先出(FIFO)的数据结构。它遵循“先进先出”(FIFO)的原则,即第一个插入的元素是第一个被删除的元素。队列适用于需要先入先出(FIFO)的数据处理。例如,操作系统的任务调度就可以用队列来实现。

下面是一个使用队列的示例代码片段:
queue = []
queue.append(1) # 插入元素1
queue.append(2) # 插入元素2
print(queue.pop(0)) # 删除并返回元素1,输出:1
print(queue.pop(0)) # 删除并返回元素2,输出:2
树
树是一种层次结构,由节点和连接节点的边组成。树中的每个节点可能有多个子节点,根节点没有父节点。树适用于需要层次结构和快速查找的情况。例如,文件系统就是用树来存储文件的。

下面是一个使用树的示例代码片段:
class TreeNode:def __init__(self, value):self.value = valueself.children = []self.parent = Noneself.is_root = Falseself.is_leaf = Falseself.level = Nonedef add_child(self, child):child.parent = selfchild.is_root = Falsechild.level = self.levelif not self.children:self.is_root = Truechild.parent = selfself.children.append(child)def get_root(node):if node.is_root:return nodeelse:return node.parent.get_root(node)
图
图是一种无限制的数据结构,由节点和连接节点的边组成。图中的节点和边可以带有权重或其他属性。图适用于需要表示复杂关系的情况。例如,社交网络就可以用图来表示。

下面是一个使用图的示例代码片段:
class Graph:
def __init__(self):
self.nodes = set()
self.edges = {}def add_node(self, node):
self.nodes.add(node)
self.edges[node] = []def add_edge(self, from_node, to_node, weight=1):
if from_node not in self.nodes or to_node not in self.nodes:
raise ValueError("Both nodes need to be in graph")
self.edges[from_node].append((to_node, weight))
self.edges[to_node].append((from_node, weight))
哈希表
哈希表是一种数据结构,它使用哈希函数将键映射到桶中,并在每个桶中存储相应的值。哈希表适用于需要快速查找键值对应关系的情况。例如,字典查找就可以用哈希表来实现。

下面是一个使用哈希表的示例代码片段:
class HashTable:
def __init__(self):
self.table = {}def put(self, key, value):
hash_key = hash(key) % len(self.table)
bucket = self.table[hash_key]
for i, kv in enumerate(bucket):
if kv[0] == key:
bucket[i] = ((key, value))
return True
return False
选择合适的算法
算法的选择同样取决于具体的问题和场景。以下是一些常见的情况和对应的算法:

- 排序算法:适用于需要对大量数据进行有序处理的情况。例如,冒泡排序、快速排序、归并排序等。
- 冒泡排序:这是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。

def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1] :arr[j], arr[j+1] = arr[j+1], arr[j]return arr
- 快速排序:这是一种分治的排序算法。它将一个数组分成两个子数组,然后对子数组进行递归排序。

def quick_sort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) // 2]left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quick_sort(left) + middle + quick_sort(right)
- 搜索算法:适用于需要在大量数据中查找特定元素的情况。例如,线性搜索、二分搜索等。
- 线性搜索:这是一种简单的搜索算法,它遍历整个数组,比较每个元素与目标元素,如果匹配则返回该元素。

def linear_search(arr, x):for i in range(len(arr)):if arr[i] == x:return ireturn -1
- 二分搜索:这是一种高效的搜索算法,它只在排序的数组中搜索,并且搜索过程是对称的。它首先检查中间元素,如果中间元素是要搜索的元素,则搜索过程结束。如果中间元素大于要搜索的元素,则在数组的左半部分继续搜索。相反,如果中间元素小于要搜索的元素,则在数组的右半部分继续搜索。

def binary_search(arr, low, high, x):if high >= low:mid = (high + low) // 2if arr[mid] == x:return midelif arr[mid] > x:return binary_search(arr, low, mid - 1, x)else:return binary_search(arr, mid + 1, high, x)else:return -1
- 图算法:适用于需要处理图形结构的情况。例如,最短路径算法(Dijkstra、Bellman-Ford等)、最小生成树算法(Kruskal、Prim等)。

这里以Dijkstra的最短路径算法为例:Dijkstra算法是一个用于解决给定节点到图中所有其他节点的最短路径问题的算法。它假设所有的边权重都是正数。
def dijkstra(graph, start_vertex):D = {v:float('infinity') for v in graph} D[start_vertex] = 0 queue = [(0, start_vertex)] while queue: current_distance, current_vertex = min(queue, key=lambda x:x[0]) queue.remove((current_distance, current_vertex)) if current_distance > D[current_vertex]: continue for neighbor, weight in graph[current_vertex].items(): old_distance = D[neighbor] new_distance = current_distance + weight if new_distance < oldDistance: D[neighbor] = newDistance queue.append((newDistance, neighbor)) return D #returns dictionary of shortest distances from start node to every other node in the graph.
- 动态规划算法:适用于需要解决复杂问题,且问题的子问题也具有独立性时的情况。例如,背包问题、最长公共子序列问题等。
以背包问题为例:背包问题是一种典型的动态规划问题,其目标是在给定背包容量和物品重量及价值的情况下,选择一系列物品装入背包以使得背包中的总价值最大。

def knapsack(weights, values, W):n = len(weights)dp = [[0 for _ in range(W+1)] for _ in range(n+1)]for i in range(1, n+1):for w in range(1, W+1):if weights[i-1] <= w:dp[i][w] = max(dp[i-1][w], dp[i-1][w-weights[i-1]] + values[i-1])else:dp[i][w] = dp[i-1][w]return dp[n][W]
- 分治算法:适用于可以将大问题分解为若干个小问题的情况。例如,归并排序、快速排序等。
这里以归并排序为例:归并排序是一种分治算法,它将一个数组分成两个子数组,然后对子数组进行递归排序,最后将两个已排序的子数组合并成一个已排序的数组。

def merge_sort(arr):if len(arr) <= 1:return arrmid = len(arr) // 2left = merge_sort(arr[:mid])right = merge_sort(arr[mid:])return merge(left, right)def merge(left, right):result = []i = j = 0while i < len(left) and j < len(right):if left[i] <= right[j]:result.append(left[i])i += 1else:result.append(right[j])j += 1result.extend(left[i:])result.extend(right[j:])return result
- 贪心算法:适用于问题的最优解可以通过一系列局部最优的选择来达到全局最优的情况。例如,霍夫曼编码、最小生成树等。
这里以霍夫曼编码为例:霍夫曼编码是一种用于数据压缩的贪心算法。它通过为每个频繁出现的字符创建一个尽可能短的编码来工作。在编码过程中,每个字符的编码是根据前一个字符的编码来确定的。

class HuffmanNode:def __init__(self, freq, char=None):self.freq = freq self.char = char self.left = None self.right = None self.huff = None def __cmp__(self, other): if(other == None): return -1 if(self.freq == other.freq): return 0 elif(self.freq > other.freq): return 1 else: return -1 def build_heap(arr): n = len(arr) for i in range(n//2 - 1, -1, -1): heapify(arr, n, i) def heapify(arr, n, i): smallest = i left = 2*i + 1 right = 2*i + 2 if left < n and arr[smallest].freq > arr[left].freq: smallest = left if right < n and arr[smallest].freq < arr[right].freq: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] # swap heapify(arr, n, smallest) # call heapify for the smallest element at root. def huffman_encode(arr): arr_min = None # to store the minimum frequency object heap = [] # to store the heap minimum at the root of heap. //创建最小堆,根节点为最小值。 //将数组转化为最小堆。 build_heap(heap) for item in arr: heap.append(item) build_heap(heap) //删除重复的元素 arr_min = heap[0] //将频率最小的元素移除 heap.remove(arr_min) //添加到 huffman tree 中 if arr_min.charif arr_min.char == None:arr_min = heap[0]heap.remove(arr_min)tree.add_node(arr_min)
else:tree.add_node(arr_min)heap.remove(arr_min)# The function to print the binary tree.
def print_binary_tree(root):if root is not None:print_binary_tree(root.left)print(root.data, end=" ")print_binary_tree(root.right)# The main function to find the Huffman编码 of a string.
def find_huffman_encoding(text):# Create a frequency table for all characters in the text.char_freq = {}for char in text:char_freq[char] = char_freq.get(char, 0) + 1# Create a priority queue to store the nodes of the Huffman tree.# The priority of a node is defined by the sum of the frequencies# of its two children.pq = []for char, freq in char_freq.items():pq.append((freq, char))heapq.heapify(pq)# Create an empty Huffman tree and add the nodes to it in a way# that maintains the property that the priority of a node is# defined by the sum of the frequencies of its two children.while len(pq) > 1:left = heapq.heappop(pq)right = heapq.heappop(pq)merge_node = HuffmanNode(left[0] + right[0], None)merge_node.left = HuffmanNode(left[0], left[1])merge_node.right = HuffmanNode(right[0], right[1])heapq.heappush(pq, merge_node)# The last element in the priority queue is the root of the Huffman tree.root = pq[-1]# Now, we can build the Huffman encoding by traversing the Huffman tree.huff_enc = []print_binary_tree(root)print("Huffman encoding for text: ")
huff_enc.reverse() # reverse the list because the traversal is in reverse order.
print(huff_enc)
这个Python程序通过创建一个优先级队列(在Python中使用heapq实现)来存储每个字符的频率,然后通过合并频率最低的两个节点来构建霍夫曼树。一旦构建了霍夫曼树,就可以使用简单的遍历来为输入字符串生成霍夫曼编码。
实践和项目
选择合适的数据结构和算法是解决实际问题的重要步骤。以下是一些实践和项目,可以帮助你锻炼和应用所学知识:
- 参与开源项目:许多开源项目都涉及到复杂的数据结构和算法。参与这些项目的开发和维护,可以帮助你了解如何在实际应用中选择和实现数据结构和算法。

- 参加算法竞赛:许多大型的算法竞赛(如ACM、Google Code Jam等)都提供了大量的难题和挑战。通过解决这些难题,你可以更深入地理解和应用各种数据结构和算法。

- 构建自己的项目:选择一个实际问题,并尝试用数据结构和算法来解决它。例如,你可以尝试实现一个基于哈希表的字典查找系统,或者实现一个基于二分搜索的查找引擎。

总之,通过参与实践和项目,你可以更深入地了解各种数据结构和算法的应用场景和优劣性,从而提高你的程序设计和问题解决能力。
🧸结尾 ❤️ 感谢您的支持和鼓励! 😊🙏
📜您可能感兴趣的内容:
- 【Java面试技巧】Java面试八股文 - 掌握面试必备知识(目录篇)
- 【Java学习路线】2023年完整版Java学习路线图
- 【AIGC人工智能】Chat GPT是什么,初学者怎么使用Chat GPT,需要注意些什么
- 【Java实战项目】SpringBoot+SSM实战:打造高效便捷的企业级Java外卖订购系统
- 【数据结构学习】从零起步:学习数据结构的完整路径
相关文章:

实践和项目:解决实际问题时,选择合适的数据结构和算法
文章目录 选择合适的数据结构数组链表栈队列树图哈希表 选择合适的算法实践和项目 🎉欢迎来到数据结构学习专栏~实践和项目:解决实际问题时,选择合适的数据结构和算法 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT…...
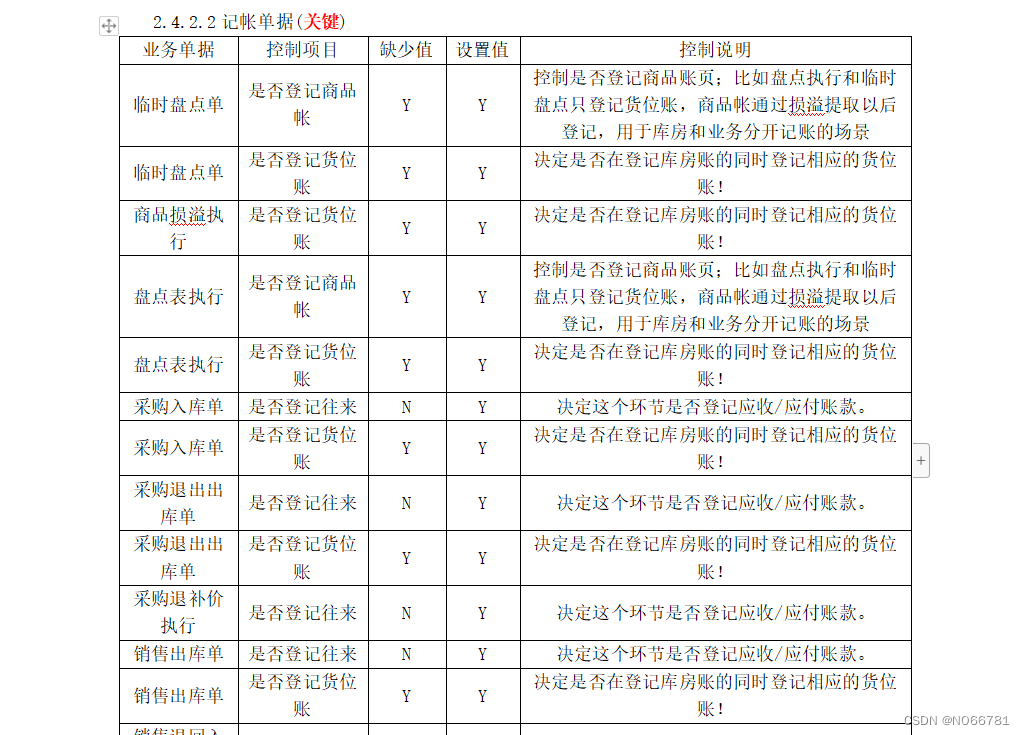
上线检查工具(待完善)
根据V11《CEBPM系统上线CheckList》整理而得,适用于V11,DHERP,Oracle和MSSQL数据库,检查内容还不完善。 上图: 1)数据库连接 2)双击[连接别名],可选择历史连接 3)主界面…...
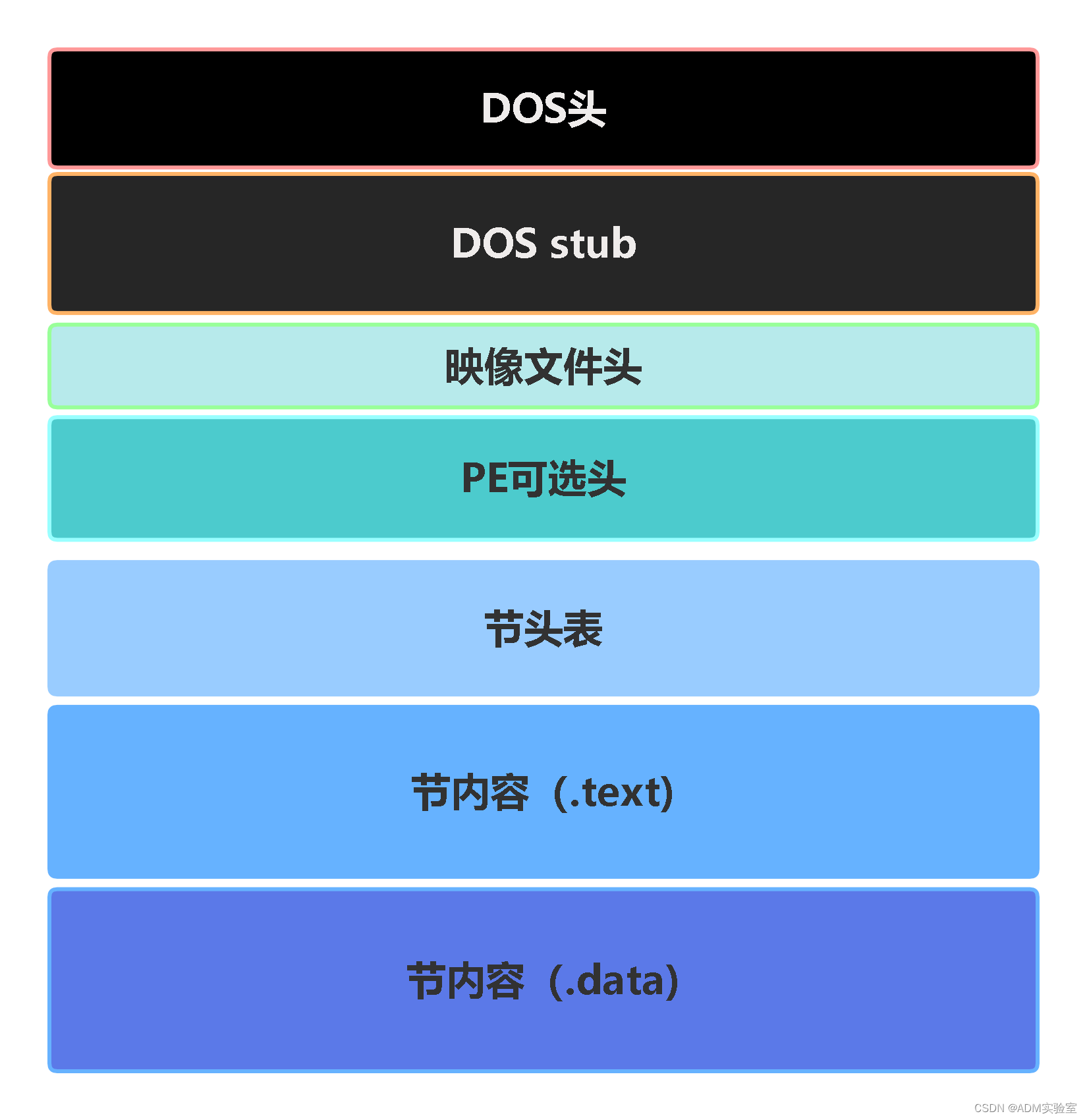
PE文件格式详解
摘要 本文描述了Windows系统的PE文件格式。 PE文件格式简介 PE(Portable Executable)文件格式是一种Windows操作系统下的可执行文件格式。PE文件格式是由Microsoft基于COFF(Common Object File Format)格式所定义的,…...

【Alibaba中间件技术系列】「RocketMQ技术专题」RocketMQ消息发送的全部流程和落盘原理分析
RocketMQ目前在国内应该是比较流行的MQ 了,目前本人也在公司的项目中进行使用和研究,借着这个机会,分析一下RocketMQ 发送一条消息到存储一条消息的过程,这样会对以后大家分析和研究RocketMQ相关的问题有一定的帮助。 分析的总体…...

关于vue首屏加载loading问题
注意:网上搜索出来的都是教你在index.html里面<div id"app"><div class"loading"></div>或者在app.vue Mounte生命周期函数控制app和loading的显示和隐藏,这里会有一个问题,就是js渲染页面需要时间,一…...

数据库性能测试实践:慢查询统计分析
01、慢查询 查看是否开启慢查询 mysql> show variables like %slow%’; 如图所示: 系统变量log_slow_admin_statements 表示是否将慢管理语句例如ANALYZE TABLE和ALTER TABLE等记入慢查询日志启用log_slow_extra系统变量 (从MySQL 8.0.14开始提供&a…...
)
windows wsl ssh 配置流程 Permission denied (publickey)
wsl ssh连接失败配置流程 1、wsl2 ifconfig的网络ip是虚拟的ip,所以采用wsl1 2、wsl1的安装教程。 3、openssh-server重装 sudo apt-get update sudo apt-get remove openssh-server sudo apt-get install openssh-server4、修改ssh配置文件 sudo vim /etc/ss…...

OpenCV(五):图像颜色空间转换
目录 1.图像颜色空间介绍 RGB 颜色空间 2.HSV 颜色空间 3.RGBA 颜色空间 2.图像数据类型间的互相转换convertTo() 3.不同颜色空间互相转换cvtColor() 4.Android JNI demo 1.图像颜色空间介绍 RGB 颜色空间 RGB 颜色空间是最常见的颜色表示方式之一,其中 R、…...

一图胜千言!数据可视化多维讲解(Python)
数据聚合、汇总和可视化是支撑数据分析领域的三大支柱。长久以来,数据可视化都是一个强有力的工具,被业界广泛使用,却受限于 2 维。在本文中,作者将探索一些有效的多维数据可视化策略(范围从 1 维到 6 维)。…...

Hbase相关总结
Hbase 1、Hbase的数据写入流程 由客户端发起写入数据的请求, 首先会先连接zookeeper 从zookeeper中获取到当前HMaster的信息,并与HMaster建立连接从HMaster中获取RegionServer列表信息 连接meta表对应的RegionServer地址, 从meta表获取当前要写入的表对应region被那个RegionS…...

C++ Primer Plus第二章编程练习答案
答案仅供参考,实际运行效果取决于运行平台和运行软件 1.编写一个C程序,它显示您的姓名和地址。 #include <iostream> using namespace std;int main() {cout << "My name is sakuraaa0908 C Primer Plus." << endl;cout &…...
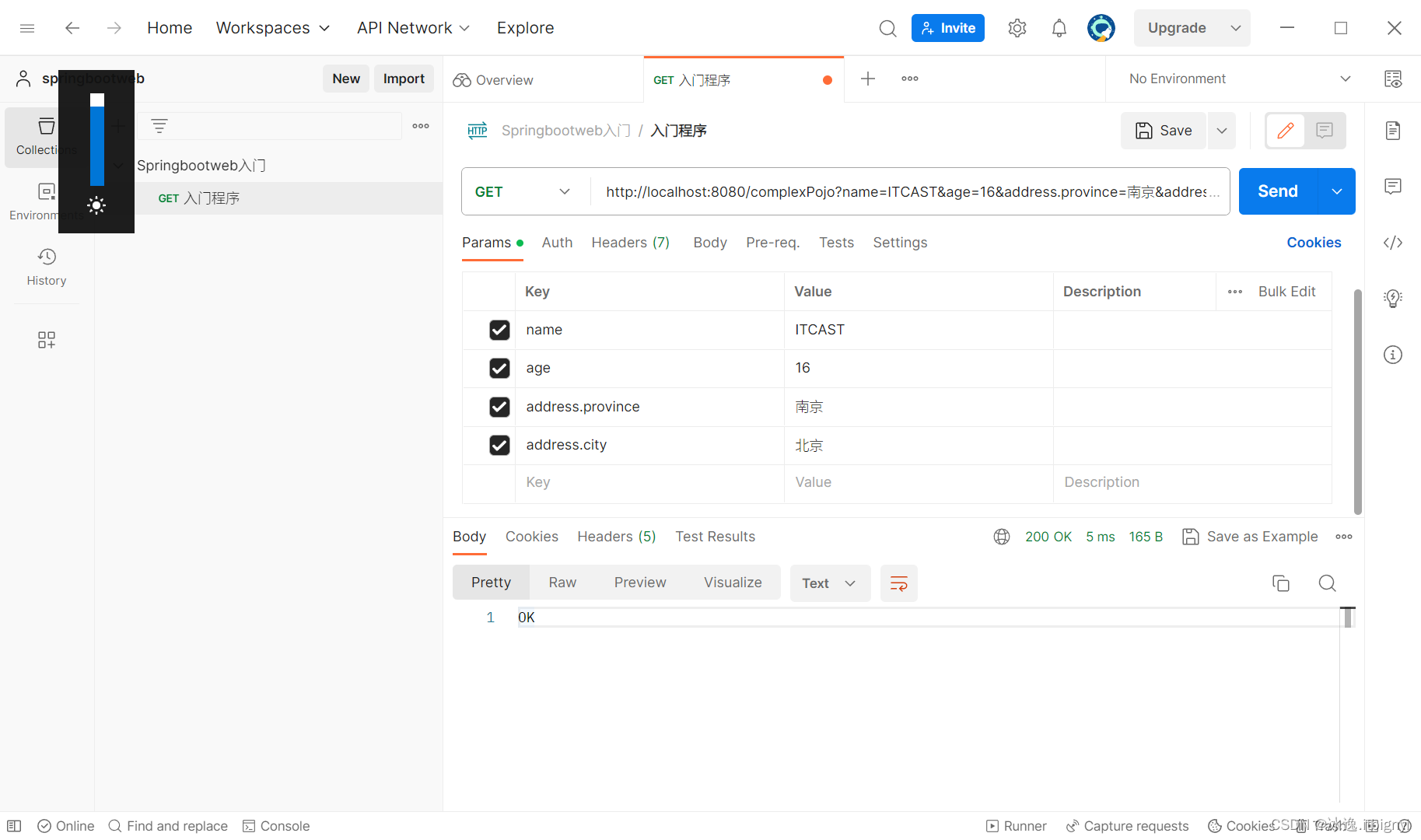
Web后端开发(请求响应)上
请求响应的概述 浏览器(请求)<--------------------------(HTTP协议)---------------------->(响应)Web服务器 请求:获取请求数据 响应:设置响应数据 BS架构:浏览器/服务器架构模式。…...

LeetCode 338. Counting Bits【动态规划,位运算】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

解释 Git 的基本概念和使用方式。
Git 是一种分布式版本控制系统,它可以跟踪文件的修改历史、协调多个人员的工作、将分支合并到一起等。下面是 Git 的一些基本概念和使用方式。 - 仓库(Repository):存储代码、版本控制历史记录等的地方。 - 分支(Bran…...
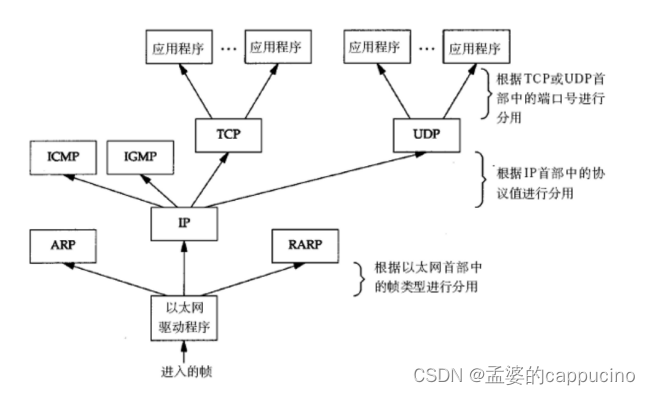
计算机网络初识
目录 1、计算机网络背景 网络发展 认识 "协议" 2、网络协议初识 OSI七层模型 TCP/IP五层(或四层)模型 3、网络传输基本流程 网络传输流程图 数据包封装和分用 4、网络中的地址管理 认识IP地址 认识MAC地址 1、计算机网络背景 网络发展 在之前呢&…...

python 笔记(2)——文件、异常、面向对象、装饰器、json
目录 1、文件操作 1-1)打开文件的两种方式: 1-2)文件操作的简单示例: write方法: read方法: readline方法: readlines方法: 2、异常处理 2-1)不会中断程序的异常捕获和处理…...
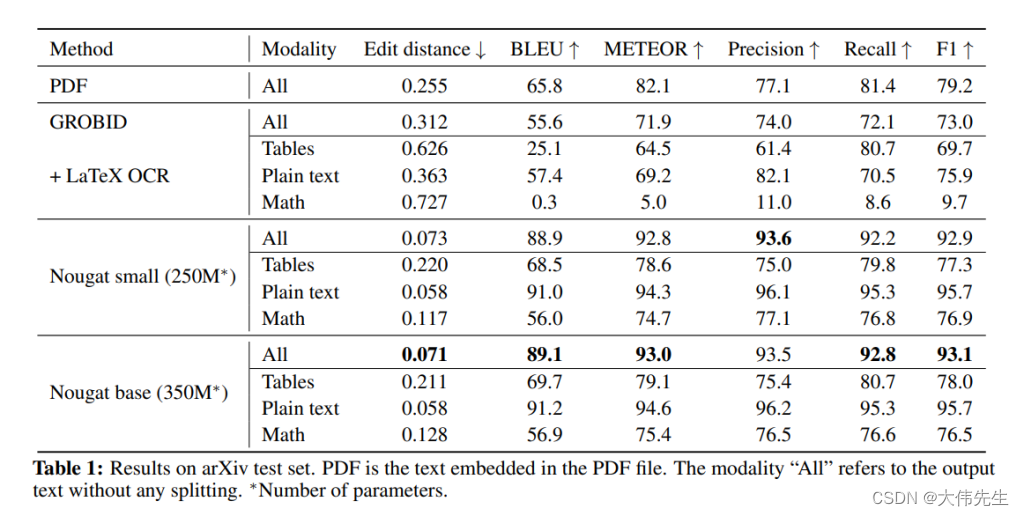
Meta AI的Nougat能够将数学表达式从PDF文件转换为机器可读文本
大多数科学知识通常以可移植文档格式(PDF)的形式存储,这也是互联网上第二突出的数据格式。然而,从这种格式中提取信息或将其转换为机器可读的文本具有挑战性,尤其是在涉及数学表达式时。 为了解决这个问题,…...

【Python爬虫笔记】爬虫代理IP与访问控制
一、前言 在进行网络爬虫的开发过程中,有许多限制因素阻碍着爬虫程序的正常运行,其中最主要的一点就是反爬虫机制。为了防止爬虫程序在短时间内大量地请求同一个网站,网站管理者会使用一些方式进行限制。这时候,代理IP就是解决方…...

50、Spring WebFlux 的 自动配置 的一些介绍,与 Spring MVC 的一些对比
Spring WebFlux Spring WebFlux 简称 WebFlux ,是 spring5.0 新引入的一个框架。 SpringBoot 同样为 WebFlux 提供了自动配置。 Spring WebFlux 和 Spring MVC 是属于竞争关系,都是框架。在一个项目中两个也可以同时存在。 SpringMVC 是基于 Servlet A…...
【算法专题突破】双指针 - 和为s的两个数字(6)
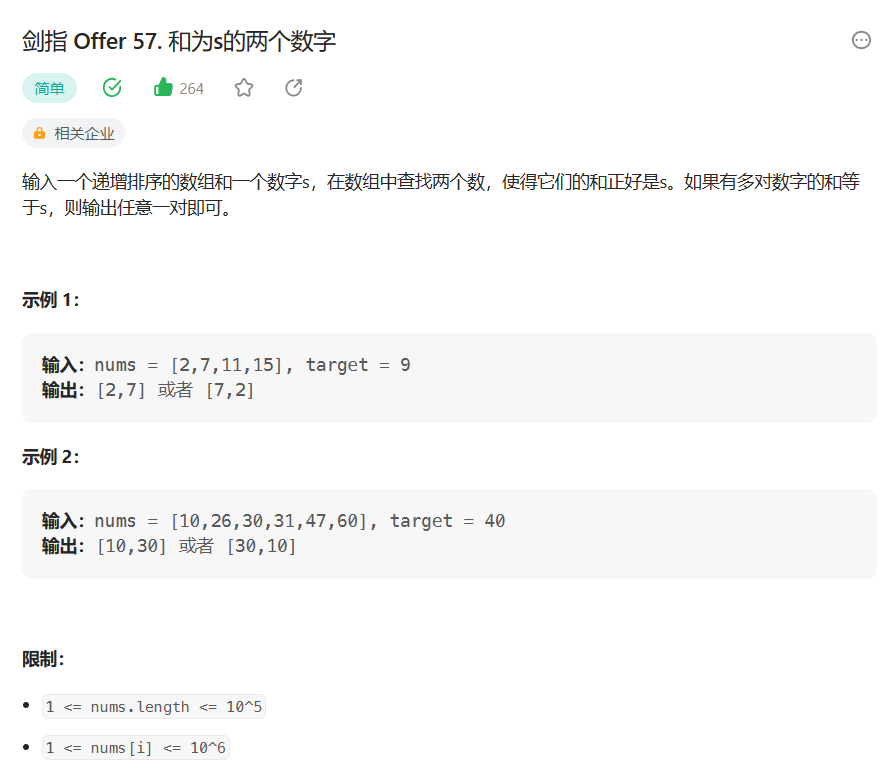
目录 1. 题目解析 2. 算法原理 3. 代码编写 写在最后: 1. 题目解析 题目链接:剑指 Offer 57. 和为s的两个数字 - 力扣(Leetcode) 这道题题目就一句话但是也是有信息可以提取的, 最重要的就是开始的那句话&#…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
