C语言malloc函数学习
malloc的全称是memory allocation,中文叫动态内存分配,用于申请一块连续的指定大小的内存块区域,以void*类型返回分配的内存区域地址;
函数原型为void *malloc(unsigned int size),在内存的动态存储区中分配一个长度为size的连续空间;函数的返回值是分配区域的起始地址;
malloc 函数返回的指针是 void * 型,在使用这个指针的时候,要进行强制类型转换;
此文有提到malloc 函数;
Win32下内存分配简单示例 - 使用CFree_bcbobo21cn的博客-CSDN博客
做一个示例,
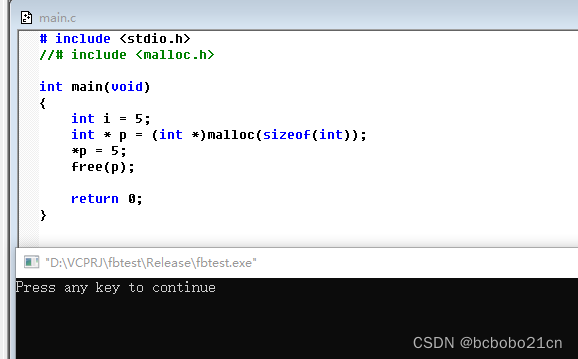
# include <stdio.h>
//# include <malloc.h> int main(void)
{int i = 5;int * p = (int *)malloc(sizeof(int));*p = 5;free(p);return 0;
}VC6中运行如下;VC6中可不用包含 <malloc.h>;
void 指针可以指向任意类型的数据,就是说可以用任意类型的指针对 void 指针赋值;
如果要将 void 指针 p 赋给其他类型的指针,则需要强制类型转换;
void 指针介绍见此;
C语言无类型指针 void* 学习_bcbobo21cn的博客-CSDN博客
相关文章:

C语言malloc函数学习
malloc的全称是memory allocation,中文叫动态内存分配,用于申请一块连续的指定大小的内存块区域,以void*类型返回分配的内存区域地址; 函数原型为void *malloc(unsigned int size),在内存的动态存储区中分配一个长度为…...
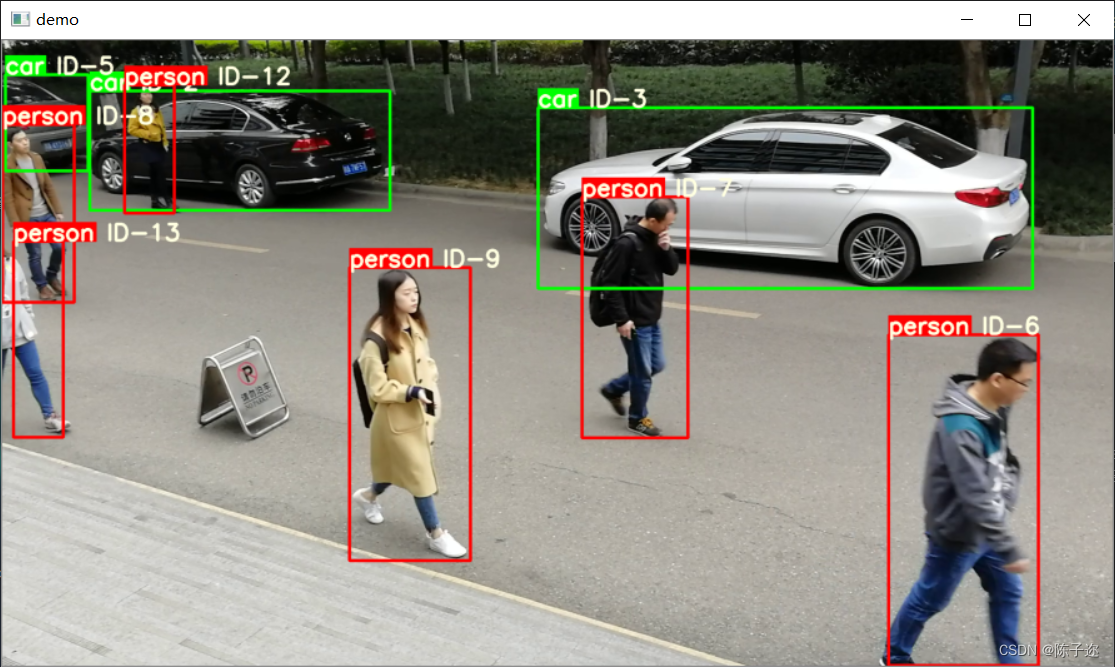
从零开始学习deepsort目标追踪算法----原理和代码详解
目录 1.目标追踪的主要步骤 2、传统sort算法的流程 3.Deepsort算法流程 4、目标追踪整体代码 4.1 Configs文件目录下: 4.2 deep_sort/deep_sort/deep目录下: 4.3 deep_sort/deep_sort/sort目录下: 运行demo: DeepSORT&…...

第三章 LInux多线程开发 3.1-3.5线程创建 终止 分离
创建线程:(好好记住 可能会叫写代码) 一般情况下,main函数所在的线程我们称之为主线程(main线程),其余创建的线程称之为子线程。 程序中默认只有一个进程,fork()函数调用,2进行 程序…...
空间曲线的参数方程
空间曲线的参数方程 二维直线 经过一点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)的方向向量为 n ( c o s θ , s i n θ ) n(cos\theta,sin\theta) n(cosθ,sinθ)的直线参数方程为: [ x y …...

非华为机型如何体验HarmonyOS鸿蒙系统 刷写HarmonyOS鸿蒙GSI系统以及一些初步的bug修复
最近很多视频网站有非华为机型使用HarmonyOS鸿蒙系统的演示。其实大都是刷了HarmonyOS鸿蒙系统gsi系统。体验还可以。有些刷入后bug较多。那么这些机型是如何刷写gsi?可以参考我以往帖子 安卓玩机搞机-----没有第三方包 刷写第三方各种GSI系统 体验非官方系统_gsi刷…...

Flutter 生成小程序的混合 App 实践
一、背景 微信小程序发展的越来越快,目前小程序甚至取代了大部分 App 的生态位,公司的坑位不增反降,只能让原生应用开发兼顾或换岗进行小程序的开发。 以我的实际情况来讲,公司应用采用的 Flutter 框架,同样的功能不可避免的就会存在 Flutter 应用开发和微信小程序开发兼…...

利用 Python-user-agents 解析 User_Agent
利用 Python-user-agents 解析 User_Agen 需求分析 近期在尝试做一个登录日志的功能,及用户登录成功后我在后台进行一个用户的登录记录,两种解决方案: 由前端得到用户的手机型号,我在后台接收后在数据库进行保存使用User_Agent…...
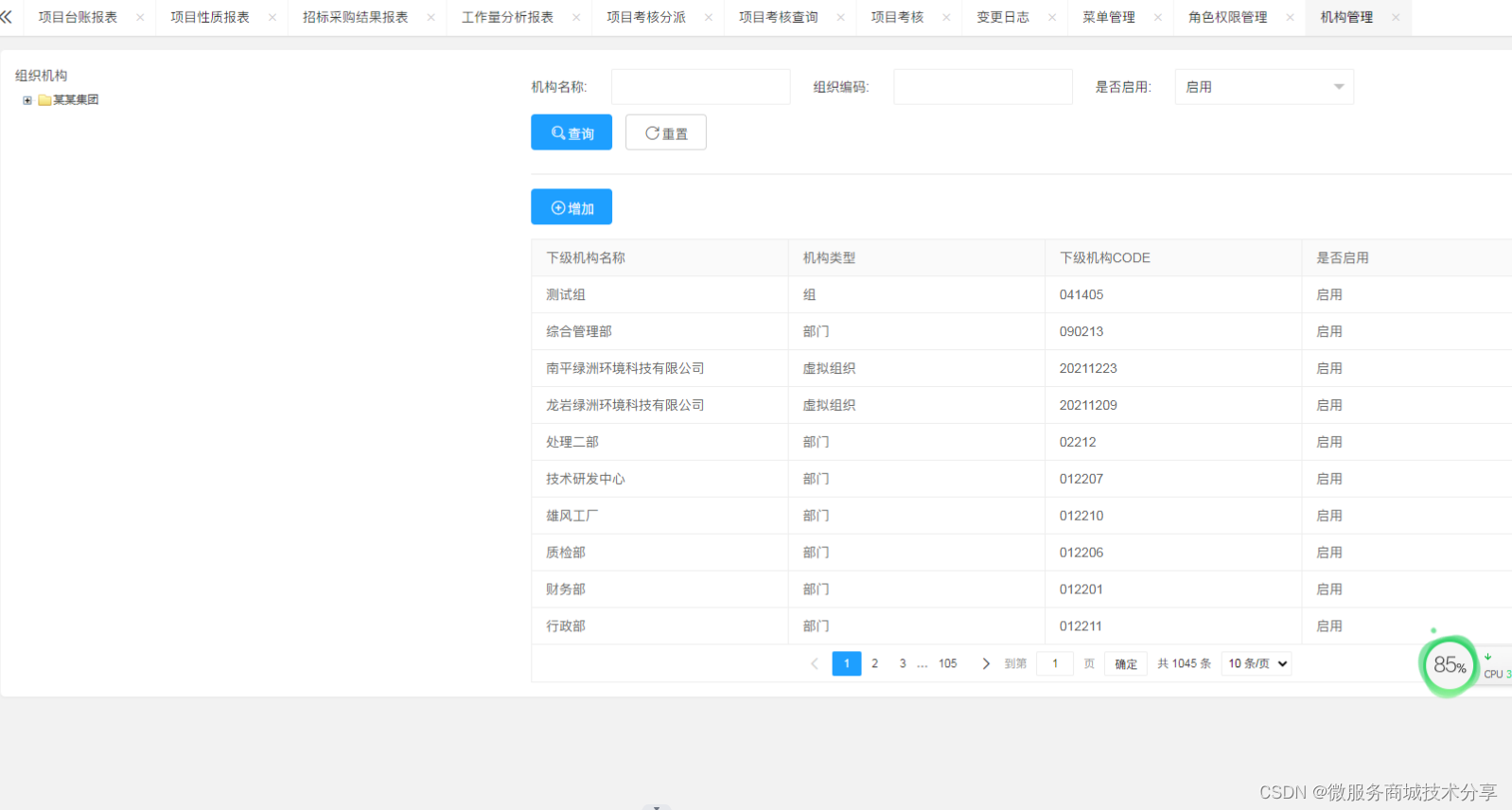
Java版企业电子招标采购系统源码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看…...

Mybatis如何给字段起别名?
Mybatis如何给字段起别名? 假如有一个学生表,有一个字段是class,你的实体类变量肯定不能用class,那么如何起别名? 通过以下代码实现 Result(column "class",property "clas")mapper代码 pub…...
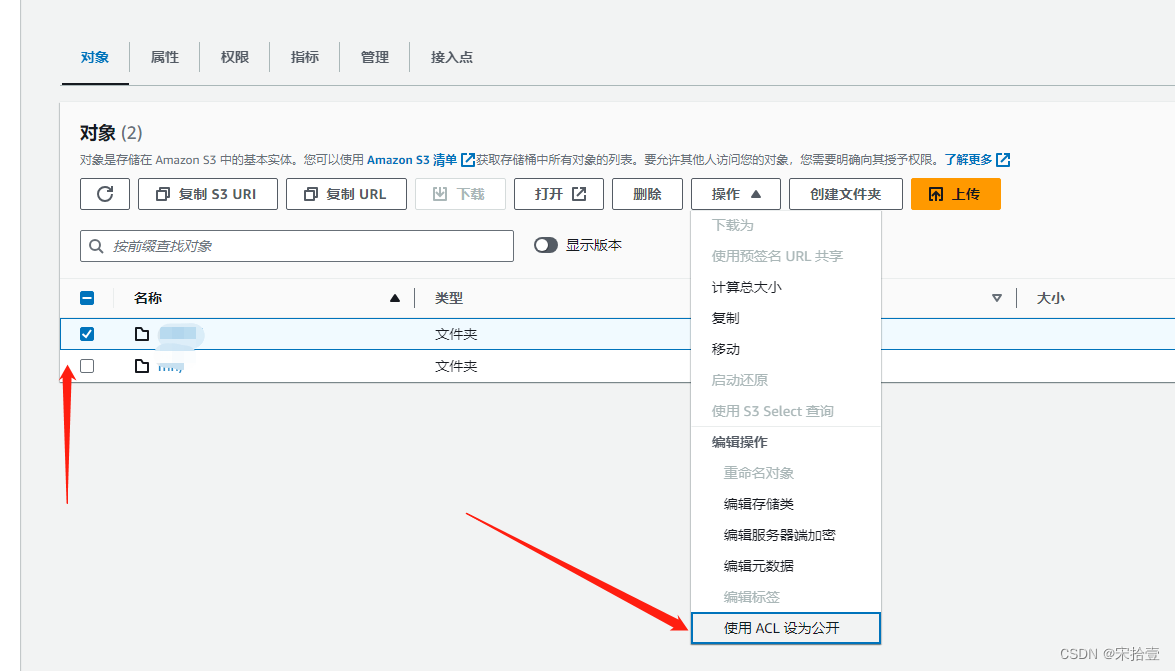
php对接AWS S3云存储,上传S3及访问权限问题
首先先下载sdk包 https://docs.aws.amazon.com/zh_cn/sdk-for-php/v3/developer-guide/getting-started_installation.html S3创建存储桶 去安全凭证-》创建访问秘钥 创建的时候会提示,主账号创建不安全,这个时候我们需要创建一个IAM账号来创建秘钥 创…...

java 实现单例模式
单例模式是一种设计模式,用于确保一个类只有一个实例,并提供一种全局访问该实例的方式。在Java中,可以使用多种方式来实现单例模式,下面整理了几种常见的实现方式。 饿汉式单例模式(Eager Initialization)&…...

minio文件服务器开启https
一、准备证书 你要有https安全证书,我的是适用于nginx的证书 私钥 xxxx.key 公钥 xxxx.pem 二、上传证书到minio服务器 然后看看你的minio docker 有没有把 /root/.minio 挂载在主机上,如果有那么把两个证书文件放在/root/.minio/certs目录里面。…...

每日刷题(回溯法经典问题之子集)
食用指南:本文为作者刷题中认为有必要记录的题目 前置知识:回溯法经典问题之组合 ♈️今日夜电波:想着你—郭顶 1:09 ━━━━━━️💟──────── 4:15 …...

PostgreSQL在进行除法时要注意
背景 整型除以整型,正常情况下当然得到的应该也是整型。数据库也是这么干的。 但是在数据库应用中,通常业务的需求是得到NUMERIC,不能直接把小数干掉。 数据库的行为给用户带来了诸多不便,例如1除以2,如果是整型除法会…...
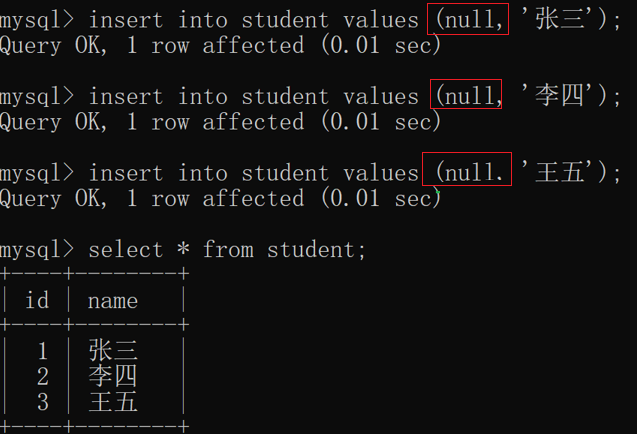
开开心心带你学习MySQL数据库之第五篇
😺欢迎来到我的博客, 记得点赞👍收藏⭐️留言✍️🐱 🐉做为一个怪兽,我的目标是少消灭一个奥特曼🐉 📖希望我写的博客对你有所帮助,如有不足,请指正📖 chatgpt 是否能够代替程序猿?…...

Geotools对geojson的解析
在 GeoTools 中,对 GeoJSON 的支持是通过一个插件来完成的,用户同样可以在 Maven 的 pom.xml 配置文件中添加下述的依赖。 <dependency><groupId>org.geotools</groupId><artifactId>gt-geojson</artifactId><version&…...

【博客701】shell实现保留网络现场:ping失败时执行mtr
shell实现保留网络现场:ping失败时执行mtr 场景 当我们网络出现抖动,到某个目的地ping不通时,我们想知道路径上哪里出现问题时可以在那时候执行mtr并保留下现场以供排查 实现:ping_and_mtr.sh #!/bin/bash# 定义要ping的IP地址列…...
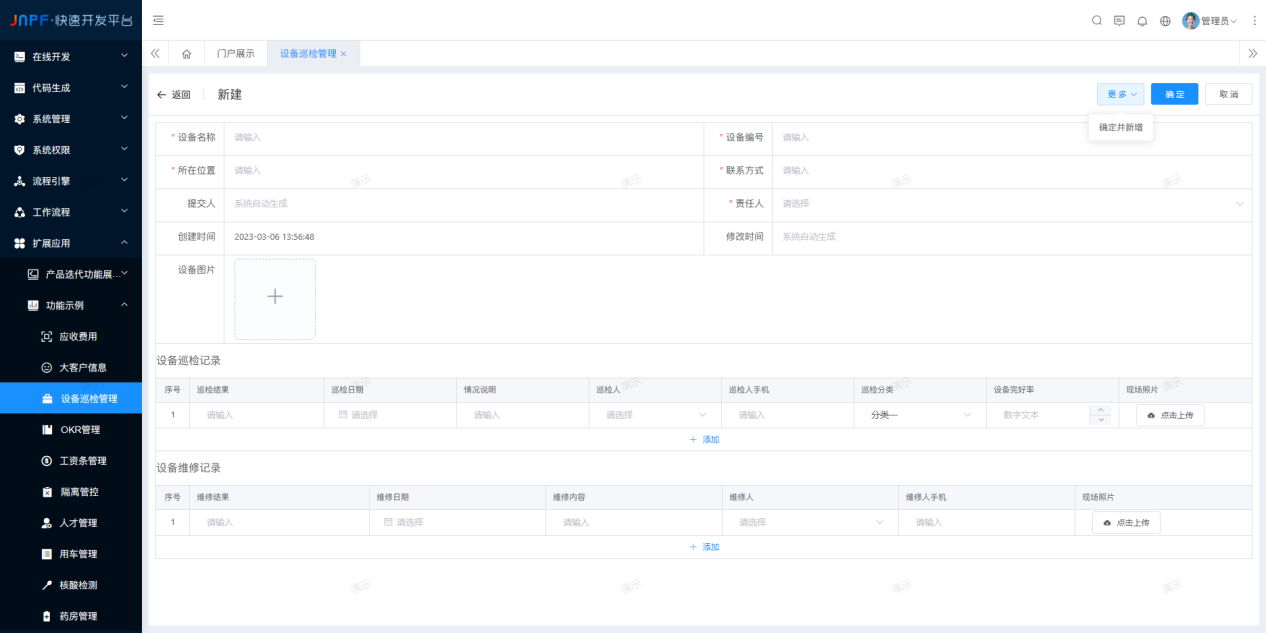
放弃手写代码吧!用低代码你能生成各种源码
很多同学不知道为什么要用Low-code做开发,传统IT开发不行么?当然可以。 传统IT自研软件开发,通过编程去写代码,还有数据库、API、第三方基础架构等。这个方式很好,但不可避免的会带来开发周期长、难度大,技…...

什么程度才算精通 Linux?
前言 Linux 的优秀之处自然不必多说。 如果将操作系统比作一辆汽车,那 Linux 就是一辆性能出色的多功能越野车,上山下海飞天无所不能。 如果你拥有了它,一定不会只满足于驾驶它上下班,不能只会挂挡、踩油门和控制方向之类的基本…...

jmeter中的__setProperty用法
__setProperty 是一个用于设置 JMeter 属性的函数,基本语法: __setProperty(property, value)** property : 是要设置的属性的名称 ** value : 是要设置的属性的值在 JMeter中,可以使用 __setProperty 函数的元素: BeanShell …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
