LeetCode 1123. 最深叶节点的最近公共祖先:DFS
【LetMeFly】1123.最深叶节点的最近公共祖先
力扣题目链接:https://leetcode.cn/problems/lowest-common-ancestor-of-deepest-leaves/
给你一个有根节点 root 的二叉树,返回它 最深的叶节点的最近公共祖先 。
回想一下:
- 叶节点 是二叉树中没有子节点的节点
- 树的根节点的 深度 为
0,如果某一节点的深度为d,那它的子节点的深度就是d+1 - 如果我们假定
A是一组节点S的 最近公共祖先,S中的每个节点都在以A为根节点的子树中,且A的深度达到此条件下可能的最大值。
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4] 输出:[2,7,4] 解释:我们返回值为 2 的节点,在图中用黄色标记。 在图中用蓝色标记的是树的最深的节点。 注意,节点 6、0 和 8 也是叶节点,但是它们的深度是 2 ,而节点 7 和 4 的深度是 3 。
示例 2:
输入:root = [1] 输出:[1] 解释:根节点是树中最深的节点,它是它本身的最近公共祖先。
示例 3:
输入:root = [0,1,3,null,2] 输出:[2] 解释:树中最深的叶节点是 2 ,最近公共祖先是它自己。
提示:
- 树中的节点数将在
[1, 1000]的范围内。 0 <= Node.val <= 1000- 每个节点的值都是 独一无二 的。
注意:本题与力扣 865 重复:https://leetcode-cn.com/problems/smallest-subtree-with-all-the-deepest-nodes/
方法一:深度优先搜索(DFS)
们把最深的叶节点的最近公共祖先,称之为 lca \textit{lca} lca节点。
编写一个函数dfs(root),返回以root为根的子树的{lca, 深度}。
-
如果左子树更深,则返回
{左子的lac, 左子深度 + 1} -
如果右子树更深,则返回
{右子的lac, 右子深度 + 1} -
否则(左右子树深度相同),则返回
{root,左子深度 + 1} -
时间复杂度 O ( n ) O(n) O(n),其中 n n n为二叉树节点个数
-
空间复杂度 O ( n ) O(n) O(n)
AC代码
C++
typedef pair<TreeNode*, int> pti;
class Solution {
private:pti dfs(TreeNode* root) {if (!root) {return {nullptr, 0};}pti left = dfs(root->left);pti right = dfs(root->right);if (left.second == right.second) {return {root, left.second + 1};}else if (left.second < right.second) {return {right.first, right.second + 1};}else {return {left.first, left.second + 1};}}
public:TreeNode* lcaDeepestLeaves(TreeNode* root) {return dfs(root).first;}
};
Python
# from typing import Optional# # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = rightclass Solution:def dfs(self, root: Optional[TreeNode]):if not root:return [None, 0]left = self.dfs(root.left)right = self.dfs(root.right)if left[1] == right[1]:return [root, left[1] + 1]elif left[1] < right[1]:return [right[0], right[1] + 1]else:return [left[0], left[1] + 1]def lcaDeepestLeaves(self, root: Optional[TreeNode]) -> Optional[TreeNode]:return self.dfs(root)[0]同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/132725441
相关文章:

LeetCode 1123. 最深叶节点的最近公共祖先:DFS
【LetMeFly】1123.最深叶节点的最近公共祖先 力扣题目链接:https://leetcode.cn/problems/lowest-common-ancestor-of-deepest-leaves/ 给你一个有根节点 root 的二叉树,返回它 最深的叶节点的最近公共祖先 。 回想一下: 叶节点 是二叉树…...
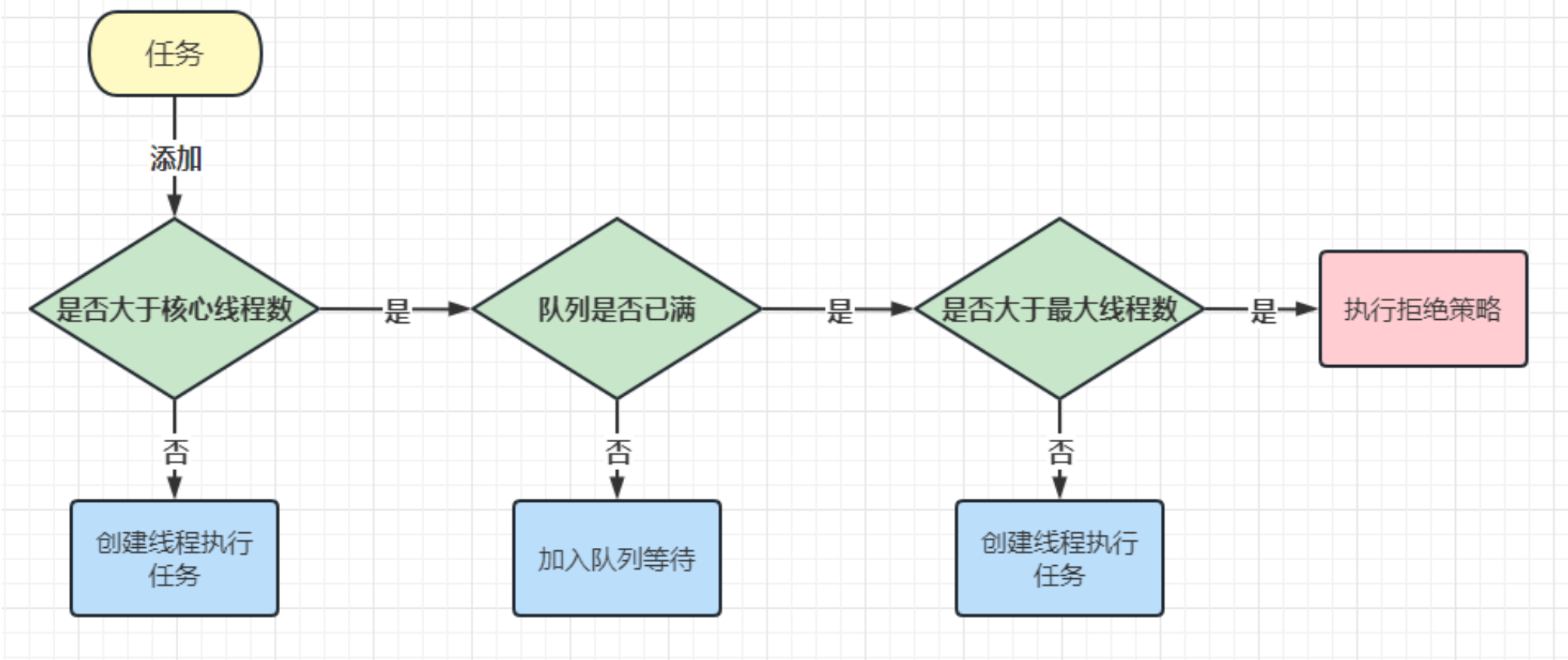
多线程应用——线程池
线程池 文章目录 线程池1.什么是线程池2.为什么要用线程池3.怎么使用线程池4.工厂模式5.自己实现一个线程池6.创建系统自带的线程池6.1 拒绝策略6.2 线程池的工作流程 1.什么是线程池 字面意思,一次创建多个线程,放在一个池子(集合类),用的时…...
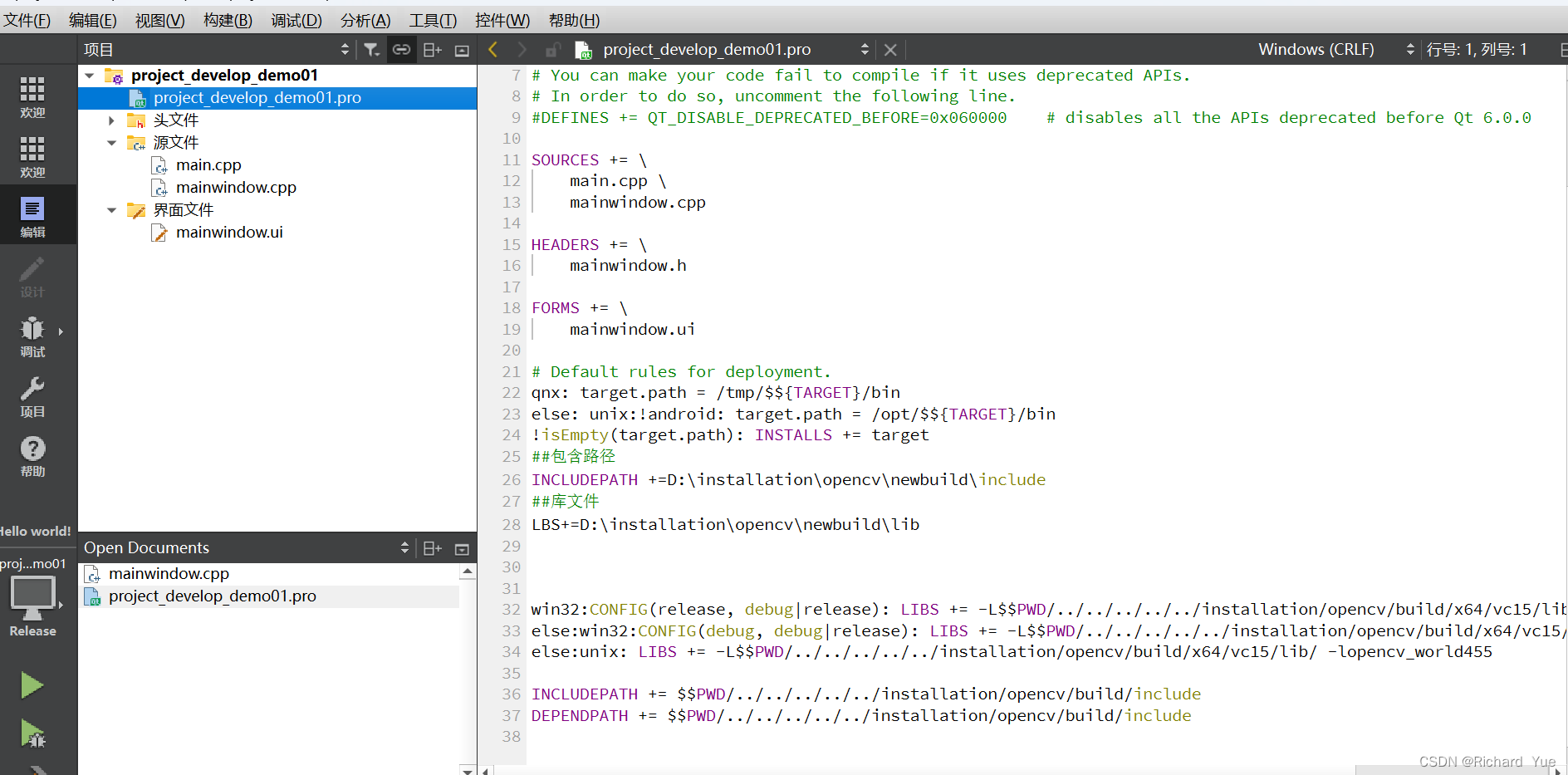
OPENCV+QT环境配置
【qtopencv开发入门:4步搞定opencv环境配置2】https://www.bilibili.com/video/BV1f34y1v7t8?vd_source0aeb782d0b9c2e6b0e0cdea3e2121eba 第一步: 安装QT Qt 5.15 第二步: 安装OPENCV VS2022 Opencv4.5.5 C 配置_愿飞翔的鱼儿的博客…...
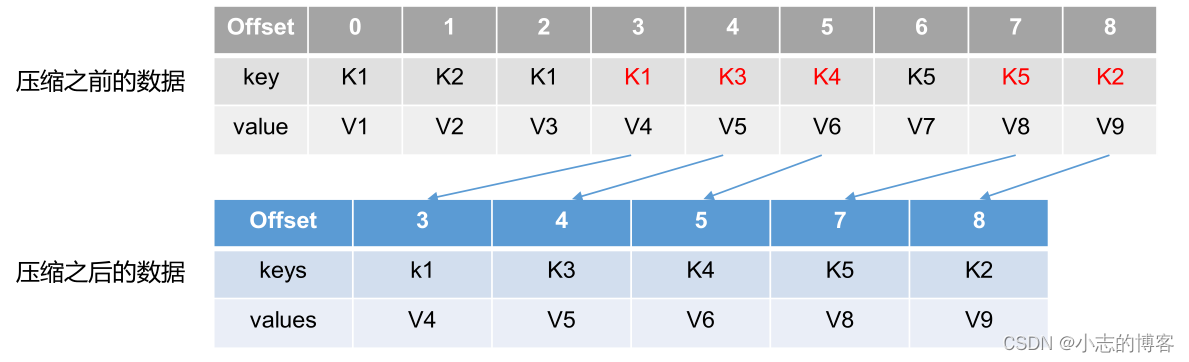
Kafka3.0.0版本——文件清理策略
目录 一、文件清理策略1.1、文件清理策略的概述1.2、文件清理策略的官方文档1.3、日志超过了设置的时间如何处理1.3.1、delete日志删除(将过期数据删除)1.3.2、compact日志压缩 一、文件清理策略 1.1、文件清理策略的概述 Kafka 中默认的日志保存时间为…...

SRT参数说明
1.超时选项 connect_timeout 连接超时时间,单位毫秒,默认值为3秒。 当RTT > 1500毫秒(2次握手交换)时,SRT无法连接。此选项适用于caller和rendezvous模式。 listen_timeout 监听超时时间,单位毫秒 timeout 为读、写和连接操作…...

vue响应式原理
vue响应式原理 vue响应式原理vue2响应式原理目标对象为数组时 vue3响应式原理Vue3和Vue2在响应式系统方面的对比数据劫持的方式支持数据劫持的数据类型Vue3响应式系统显著优点是: vue响应式原理 无论vue2和vue3响应式都是通过观察者模式(发布订阅模式&a…...
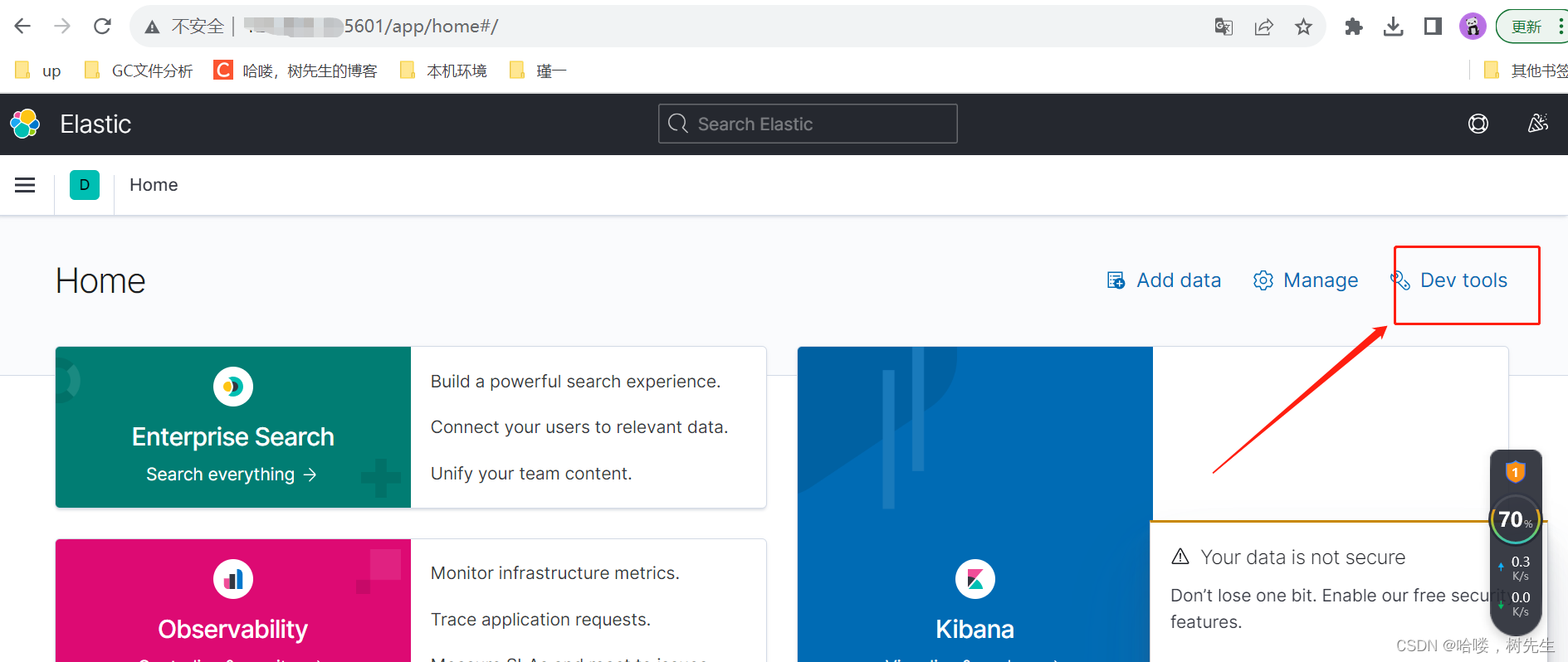
elk安装篇之 Kibana安装
Kibana是一个开源的分析与可视化平台,设计出来用于和Elasticsearch一起使用的。你可以用kibana搜索、查看存放在Elasticsearch中的数据。是es的可视化客户端之一。 一:下载 https://www.elastic.co/cn/kibana 我的es是elasticsearch-7.10.2版本&#x…...

MySQL 用户授权管理及白名单
1.创建用户 在 MySQL 中,你可以通过以下步骤创建用户并设置白名单: 使用管理员账号连接到 MySQL 服务器。 创建新用户: CREATE USER usernamehostname IDENTIFIED BY password;其中, username 是你要创建的用户名;ho…...

pc-签字画板vue-esign的使用
使用的是vue-esign组件 npm install vue-esign 首先下载组件在main.js中引入vue-esign,并且挂载 import { createApp } from vue; import App from ./App.vue; const app createApp(App);import vueEsign from vue-esign app.use(vueEsign ) 页面使用࿰…...
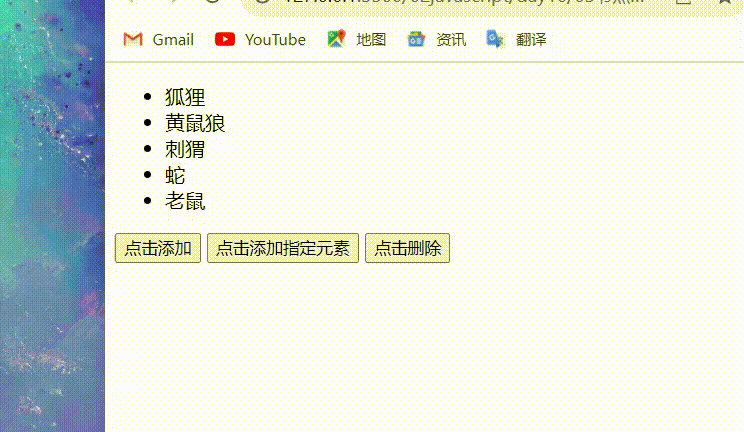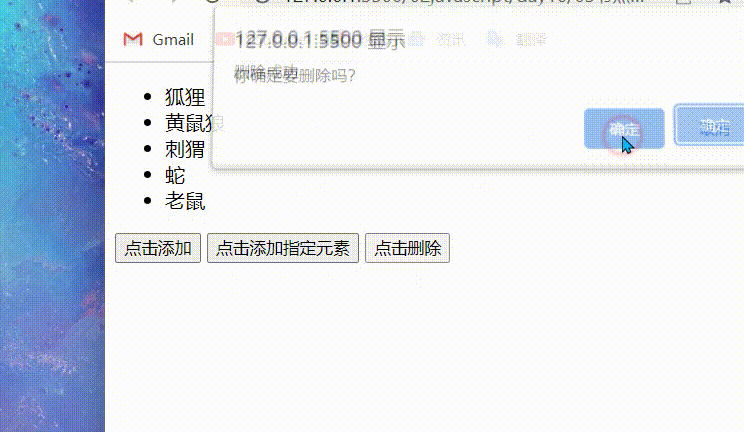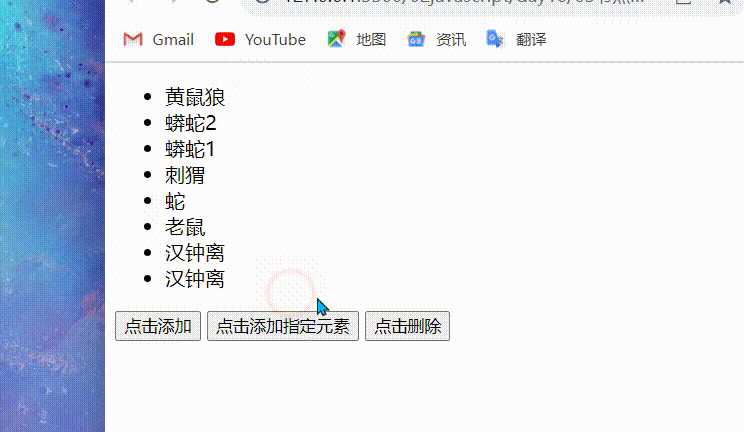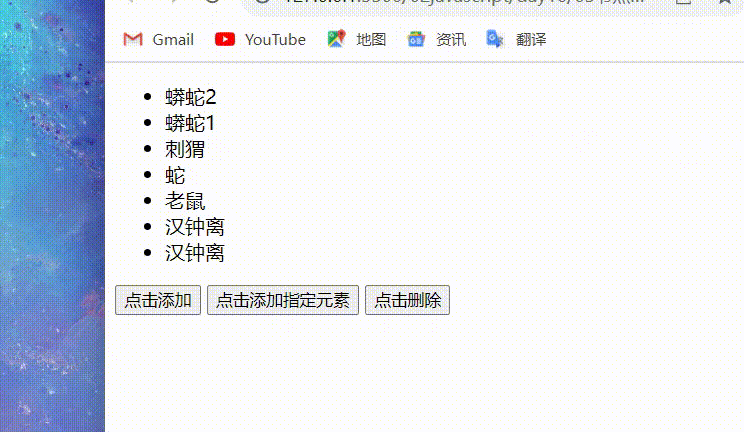
javaScript:节点操作
目录 前言 常用的节点操作 innerHTML 的两个弊端(补充) createElement(标签名)使用dom方法创建一个元素 父元素.appendChild(子元素) 添加到父元素 注意 指定插入 父元素.insertBefore(要添加的元素,父元素中的指定子元素) 注意&…...

git 忽略已经提交的文件或文件夹 (修改.gitignore文件无效)
场景描述:项目开发到一半,追加了模块,提交的时候未注意将不需要提交的文件或者目录提交到.gitignore,然后提交后发现再修改git配置文件已无法阻拦更新,查阅官方资料: 核心点:.gitignore 之前&a…...

学习左耳听风栏目90天——第十二天 12/90(学习左耳朵耗子的工匠精神,对技术的热爱)【时间管理:同扭曲时间的事儿抗争】
时间管理:同扭曲时间的事儿抗争 要学会说不...
前端如何将后台数组进行等分切割
前端如何切割数组 目标:前端需要做轮播,一屏展示12个,后端返回的数组需要进行切割,将数据以12为一组进行分割 环境:vue3tselement plus 代码如下: function divideArrayIntoEqualParts(array, chunkSiz…...

如何有效防止服务器被攻击?
随着互联网的快速发展,服务器安全问题日益引起人们的关注。近期,全球范围内频繁发生的服务器攻击事件引发了广泛关注。为了保护企业和个人的数据安全,有效防止服务器被攻击已成为迫在眉睫的任务。 首先,及时更新服务器的操作系统和…...
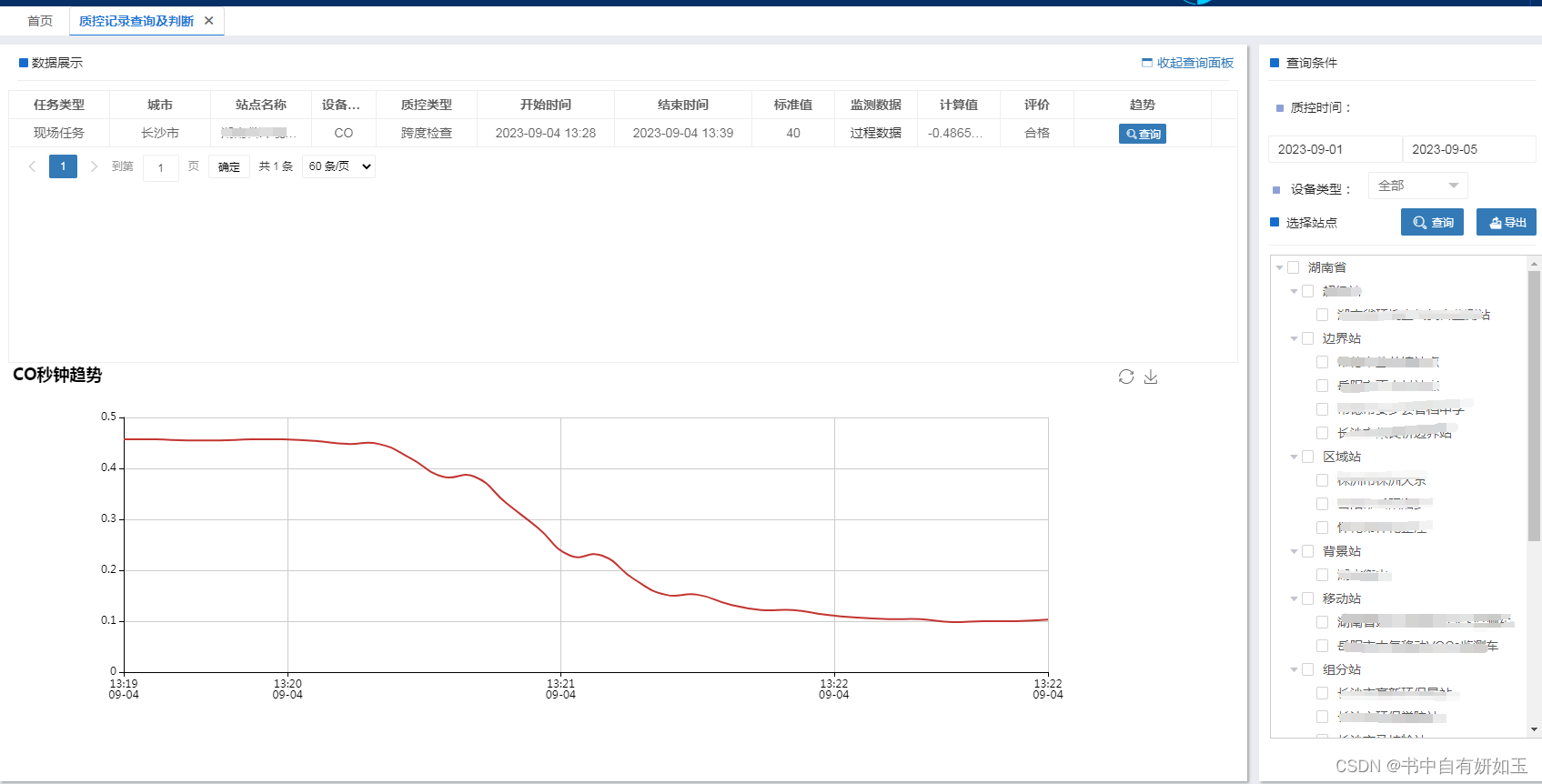
layui表格高度
layui表格的高度设置时使用 height:‘full’ 高度就是表格每个页面的总高度。也可以直接写数值,但是这是定高。 也可以使用 height:“full-数值”,比如 height:full-80 那么就会在表格占据剩余div的时候底部留100px。相当于margin-bottom:10…...
一文1800字从0到1使用Python Flask实战构建Web应用
Python Flask是一个轻量级的Web框架,它简单易用、灵活性高,适用于构建各种规模的Web应用。本文将介绍如何使用Python Flask框架来实战构建一个简单的Web应用,并展示其基本功能和特性。 第一部分:搭建开发环境 在开始之前我们需要…...
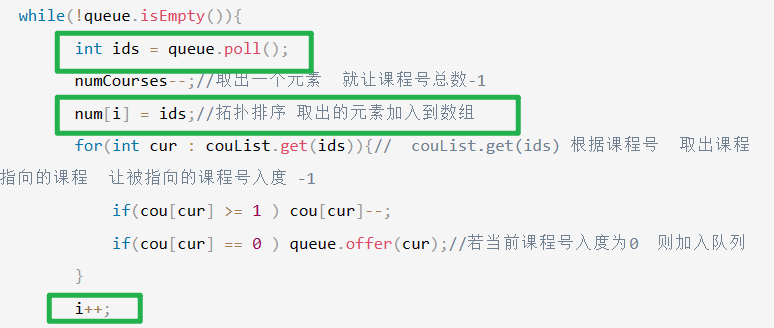
【LeetCode-中等题】210. 课程表 II
文章目录 题目方法一:bfs方法二:dfs 题目 这一题是在207题的基础上,要统计拓扑排序的顺序集合,所以只需要在207的基础上加入一个将拓扑排序的节点输出即可(有环无拓扑排序) 【LeetCode-中等题】207. 课程表…...

vue修饰符的用法
Vue修饰符是指在Vue模板中用于改变指令行为的特殊后缀。修饰符以.开头,用于指示指令应该如何绑定或响应事件。Vue修饰符在一些常见的指令中使用,例如v-on和v-model。常见的Vue修饰符包括: .prevent:阻止默认事件的发生。.stop&am…...

汽车3D HMI图形引擎选择
2002年,电影《少数派报告》让观众深入了解未来。 除了情节的核心道德困境之外,大多数人都对它的技术着迷。 我们看到了自动驾驶汽车、个性化广告和用户可以无缝交互的 3D 计算机界面。 令人惊讶的是,虽然故事发生在 2054 年,但许多科幻想象的作品已经成为现实。 对于汽车和…...

stable diffusion实践操作-webUI教程-不是基础-是特例妙用
系列文章目录 stable diffusion实践操作 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、SD webUI是什么?二、详细教程1. 相关插件安装1.1. 提示词插件安装和使用1.2 tagg标签妙用…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...
