Kotlin 环境下解决属性初始化问题

🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁
🦄 博客首页——🐅🐾猫头虎的博客🎐
🐳 《面试题大全专栏》 🦕 文章图文并茂🦖生动形象🐅简单易学!欢迎大家来踩踩~🌺
🌊 《IDEA开发秘籍专栏》 🐾 学会IDEA常用操作,工作效率翻倍~💐
🌊 《100天精通Golang(基础入门篇)》 🐅 学会Golang语言,畅玩云原生,走遍大小厂~💐
🪁🍁 希望本文能够给您带来一定的帮助🌸文章粗浅,敬请批评指正!🐅🐾🍁🐥
文章目录
- 🐱🐯 猫头虎博主的技术分享
- Kotlin 环境下解决属性初始化问题
- 摘要
- 引言
- 解决方案
- 1. 使用可空的`Int`类型
- 2. 为属性提供非空的默认值
- 3. 在setter中进行非空检查
- 总结
- 参考资料
- 原创声明

🐱🐯 猫头虎博主的技术分享
Kotlin 环境下解决属性初始化问题
摘要
在本文中,我们将探讨如何在 Kotlin 中适当地处理属性的初始化问题,特别是当你面对null值和基本数据类型的组合时。我们还将通过一些代码示例来展示每个方法的应用。
引言
有时候,我们会在编程时遇到这样的情况:一个原本应该是基本数据类型的属性(如Int)被赋值为null。在这种情况下,Kotlin 如何帮助我们优雅地处理这种情况呢?
解决方案
1. 使用可空的Int类型
这样你就可以为属性赋值null。
var paperType: Int? = null
2. 为属性提供非空的默认值
这样即使你不显式地初始化它,它也不会为null。
var paperType: Int = 0
3. 在setter中进行非空检查
这样在试图为属性赋值null时,你可以给它一个默认值或者抛出异常。
var paperType: Int = 0set(value) {field = value ?: 0 // 或任何其他默认值}
总结
Kotlin 为我们提供了多种方法来处理可能出现的null问题,从而确保我们的代码更加健壮。选择哪种方法取决于你的具体业务需求和逻辑。
参考资料
- Kotlin 官方文档 - 可空类型
- Kotlin 官方文档 - 属性与字段
希望你们喜欢这篇博客!如果有任何问题或建议,请在下方留言。🐱🚀🚀🔧🔍
原创声明
======= ·
- 原创作者: 猫头虎
作者wx: [ libin9iOak ]
| 学习 | 复习 |
|---|---|
| ✔ | ✔ |
本文为原创文章,版权归作者所有。未经许可,禁止转载、复制或引用。
作者保证信息真实可靠,但不对准确性和完整性承担责任。
未经许可,禁止商业用途。
如有疑问或建议,请联系作者。
感谢您的支持与尊重。
点击
下方名片,加入IT技术核心学习团队。一起探索科技的未来,共同成长。
相关文章:

Kotlin 环境下解决属性初始化问题
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
Java复习-20-接口(3)- 代理设计模式
代理设计模式(Proxy) 功能:可以帮助用户将所有的开发注意力只集中在核心业务功能的处理上。 代理模式(Proxy Pattern)是一种结构性模式。代理模式为一个对象提供了一个替身,以控制对这个对象的访问。即通过代理对象访问目标目标对象,可以在目…...

如何远程访问Linux MeterSphere一站式开源持续测试平台
文章目录 前言1. 安装MeterSphere2. 本地访问MeterSphere3. 安装 cpolar内网穿透软件4. 配置MeterSphere公网访问地址5. 公网远程访问MeterSphere6. 固定MeterSphere公网地址 前言 MeterSphere 是一站式开源持续测试平台, 涵盖测试跟踪、接口测试、UI 测试和性能测试等功能&am…...

LinuxUbuntu安装OpenWAF
Linux&Ubuntu安装OpenWAF 官方GitHub地址 介绍 OpenWAF(Web Application Firewall)是一个开源的Web应用防火墙,用于保护Web应用程序免受各种网络攻击。它通过与Web服务器集成,监控和过滤对Web应用程序的流量,识…...

LeetCode 剑指offer 09.用两个栈实现队列
LeetCode 剑指offer 09.用两个栈实现队列 题目描述 用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回…...

第三方软件检测机构有哪些资质,2023年软件测评公司推荐
软件第三方测试报告 伴随着软件行业的蓬勃发展,软件测试也迎来了热潮,但是国内的软件测试行业存在着测试入行门槛低、测试投入少、测试人员专业性不足等问题,这些问题不但会阻碍软件测试行业的良性发展,而且难以保证软件产品的质…...

Unity的GPUSkinning进一步介绍
大家好,我是阿赵。 在几年前,我曾经写过一篇介绍GPUSkinning的文章,这么多年之后,还是看到不停有朋友在翻看这篇旧文章。今天上去GitHub看了一下,GPUSkinning这个开源的插件已经很久没有更新过了,还是停…...
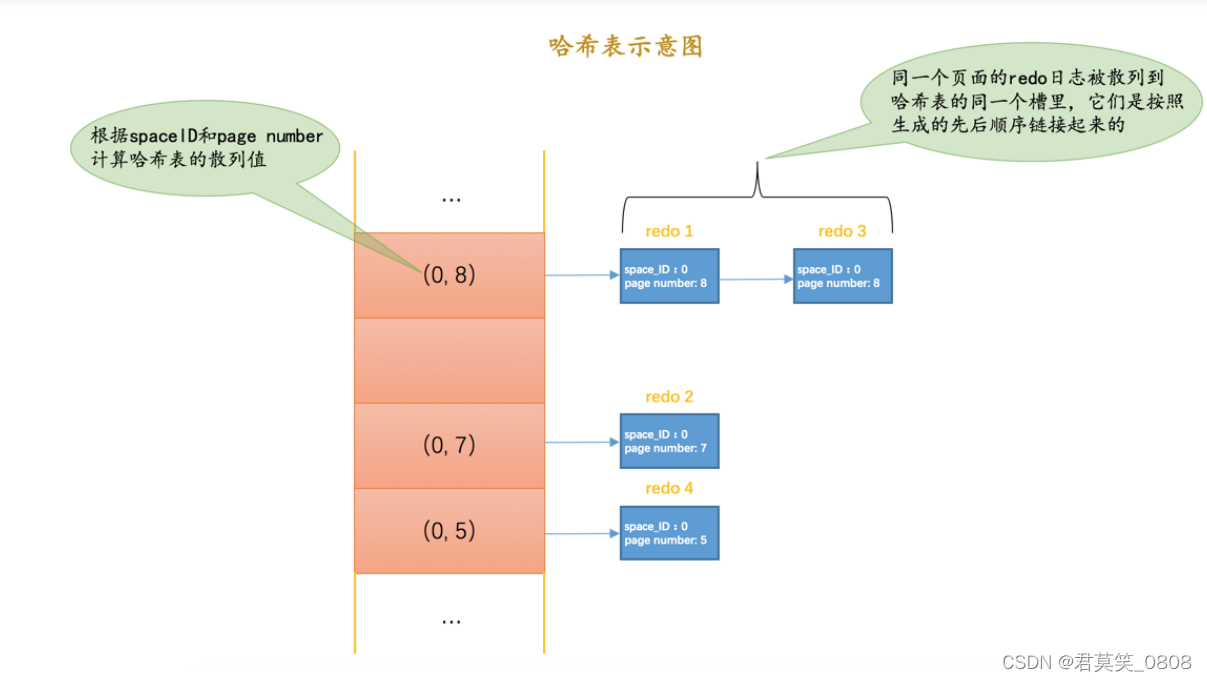
Mysql redolog
一、redolog 是啥 数据库的ACID:A原子性,C一致性,I隔离性,D持久性; redolog:保证 持久性; redolog: 系统奔溃重启时需要按照上述内容所记录的步骤重新更新数据页,特点:…...
【设计模式】Head First 设计模式——桥模式 C++实现
设计模式最大的作用就是在变化和稳定中间寻找隔离点,然后分离它们,从而管理变化。将变化像小兔子一样关到笼子里,让它在笼子里随便跳,而不至于跳出来把你整个房间给污染掉。 设计思想 桥模式。将抽象部分(业务功能)与实现部分(平…...
CESM2代码下载
这半年忙着毕业写论文,好久好久好久不更新了∠( ω)/ ,今天准备开个新坑 ๑乛◡乛๑,学习一下CESM(Community Earth System Model),它是一个完全耦合的全球气候模型,可用于地球过去、…...

编写OpenCL程序的基本步骤
opencl pyopencl OpenCL-Headers OpenCL(全称为Open Computing Langugae,开放运算语言)是第一个面向异构系统(此系统中可由CPU,GPU或其它类型的处理器架构组成)的并行编程的开放式标准。 它是跨平台的。 OpenCL由两部分组成,一是用于编写…...

计算机网络之TCP/IP协议第一篇:网络基础知识
文章目录 写给自己的话 一:前言 1:手握金刚钻的TCP/IP 2:计算机中的协议 3:分组...
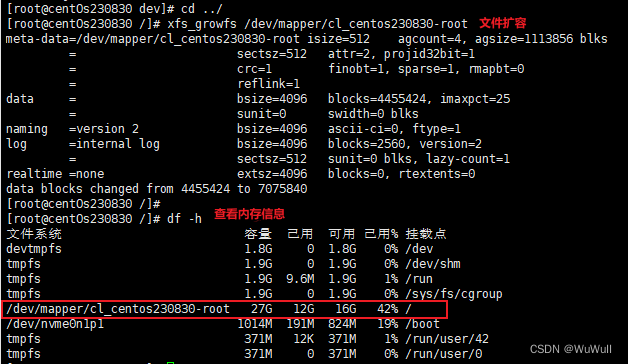
虚拟机扩容
系统环境centos8,分两步,第一步先在vmware扩容,第二部在虚拟机内部扩容 1.vmware分配磁盘空间 2.虚拟机内部扩容 查看当前磁盘信息,这个是扩容之前的,扩容完成才会显示新的 df -h查看系统分区信息 fdisk -l查看目录…...
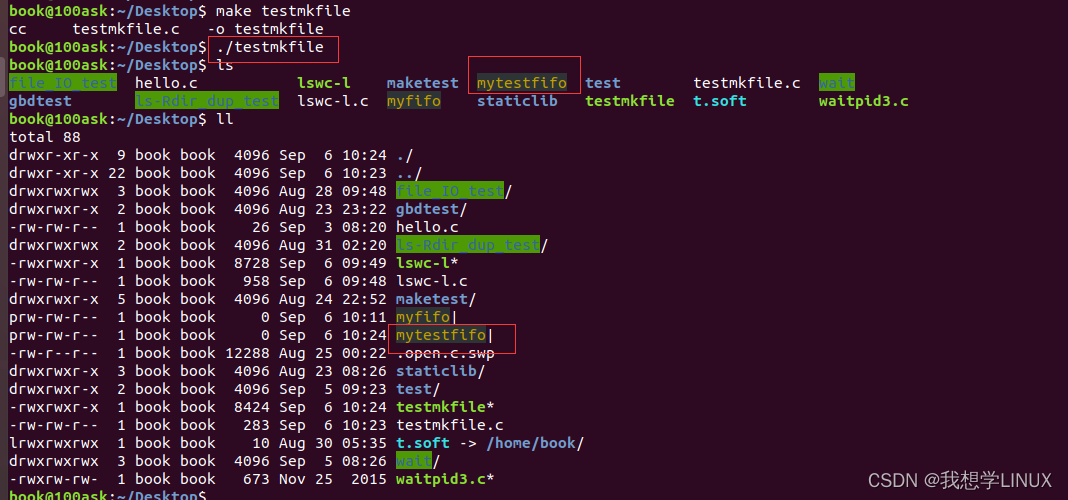
Linux下的系统编程——进程间的通信(九)
一、进程间通信常用方式 IPC方式: Linux环境下,进程地址空间相互独立,每个进程各自有不同的用户地址空间。任何一个进程的全局变量在另一个进程中都看不到,所以进程和进程之间不能相互访问,要交换数据必须通过内核&am…...

Qt QtableWidget、QtableView表格删除选中行、删除单行、删除多行
文章目录 Qt QtableWidget表格删除选中行只能选择一行,点击按钮后,删除一行可以选择中多行,点击按钮后,删除多行选中某一列中的不同行,点击按钮后,删除多行 QTableWidgetSelectionRange介绍QTableWidget的选…...
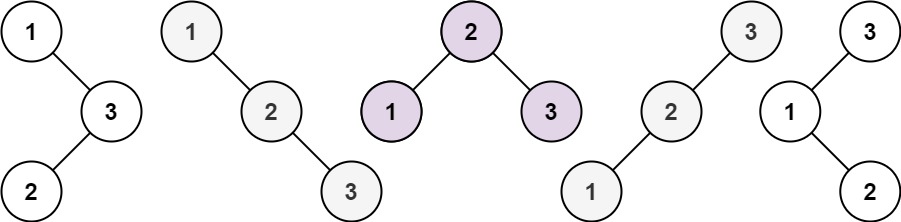
【代码随想录day24】不同的二叉搜索树
题目 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5示例 2: 输入:n 1 输出…...
数学建模--Subplot绘图的Python实现
目录 1.Subplot函数简介 2.Subplot绘图范例1:绘制规则子图 3.Subplot绘图范例2:绘制不规则子图 4.Subplot绘图范例3:gridspec辅助实战1 5.Subplot绘图范例4:gridspec辅助实战2 1.Subplot函数简介 """ 最近在数学建模种需要绘制多张子图,发现对于subplot函…...
JMeter(三十九):selenium怪异的UI自动化测试组合
文章目录 一、背景二、JMeter+selenium使用过程三、总结一、背景 题主多年前在某社区看到有人使用jmeter+selenium做UI自动化测试的时候,感觉很是诧异、怪异,为啥?众所周知在python/java+selenium+testng/pytest这样的组合框架下,为啥要选择jmeter这个东西[本身定位是接口测…...

c++ 移动构造方法为什么要加noexcept
背景: 最近看了候捷老师的c的教程, 他说移动构造方法要加noexcept, 在vector扩容的时候, 如果有移动构造方法没有加noexcept,是不会调用的. 个人感觉有些神奇, 这就去查下一探究竟. 过程: 测试代码如下: #include <iostream> #include <vector> struct A {A(){s…...
鸿鹄工程项目管理系统 Spring Cloud+Spring Boot+前后端分离构建工程项目管理系统
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&am…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
