【代码随想录day24】不同的二叉搜索树
题目
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
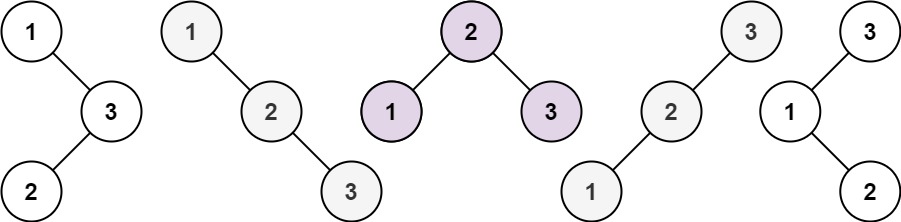
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
代码
定义dp[i]为由i个节点组成的二叉排序树有dp[i]种。
我们可以从节点数i为2开始遍历,每次遍历分别用j表示根节点左子树有j个节点,那对应右子树就有i-j-1个节点,那么左右子树分别能够组成的二叉排序树就是dp[j]和dp[i-j-1]种 ,j的取值范围是从0到i-1。题目要求的就是dp[j]*dp[i-j-1]。
这里当左右子树有为空的时候,我们应该把他当成1,不然dp[j]*dp[i-j-1]就是0了,但这种情况也是合理的,因此处理一下得到:dp[i]+=max(1,dp[j])*max(1,dp[i-j-1])。
class Solution:def numTrees(self, n: int) -> int:dp = [0 for _ in range(n+1)]dp[1]=1for i in range(2,n+1):for j in range(i):dp[i]+=max(1,dp[j])*max(1,dp[i-j-1])return dp[n]
相关文章:

【代码随想录day24】不同的二叉搜索树
题目 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5示例 2: 输入:n 1 输出…...
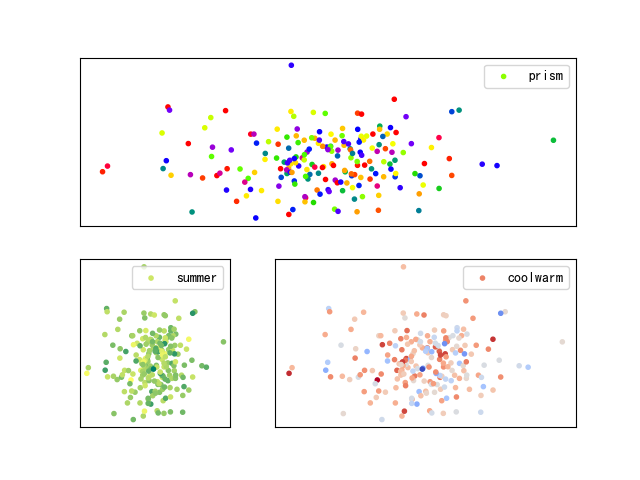
数学建模--Subplot绘图的Python实现
目录 1.Subplot函数简介 2.Subplot绘图范例1:绘制规则子图 3.Subplot绘图范例2:绘制不规则子图 4.Subplot绘图范例3:gridspec辅助实战1 5.Subplot绘图范例4:gridspec辅助实战2 1.Subplot函数简介 """ 最近在数学建模种需要绘制多张子图,发现对于subplot函…...
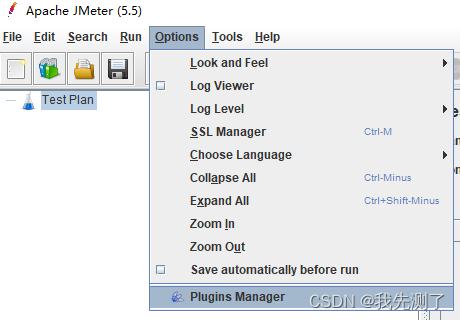
JMeter(三十九):selenium怪异的UI自动化测试组合
文章目录 一、背景二、JMeter+selenium使用过程三、总结一、背景 题主多年前在某社区看到有人使用jmeter+selenium做UI自动化测试的时候,感觉很是诧异、怪异,为啥?众所周知在python/java+selenium+testng/pytest这样的组合框架下,为啥要选择jmeter这个东西[本身定位是接口测…...

c++ 移动构造方法为什么要加noexcept
背景: 最近看了候捷老师的c的教程, 他说移动构造方法要加noexcept, 在vector扩容的时候, 如果有移动构造方法没有加noexcept,是不会调用的. 个人感觉有些神奇, 这就去查下一探究竟. 过程: 测试代码如下: #include <iostream> #include <vector> struct A {A(){s…...
鸿鹄工程项目管理系统 Spring Cloud+Spring Boot+前后端分离构建工程项目管理系统
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&am…...
手把手教你搭建园林园艺小程序商城
现如今,随着互联网的快速发展,小程序成为了企业和个人展示产品和服务的新方式。在园林园艺行业,构建一个园林园艺小程序能够更好地推广和销售自己的产品和服务。那么,如何构建一个园林园艺小程序呢?下面我们来详细介绍…...
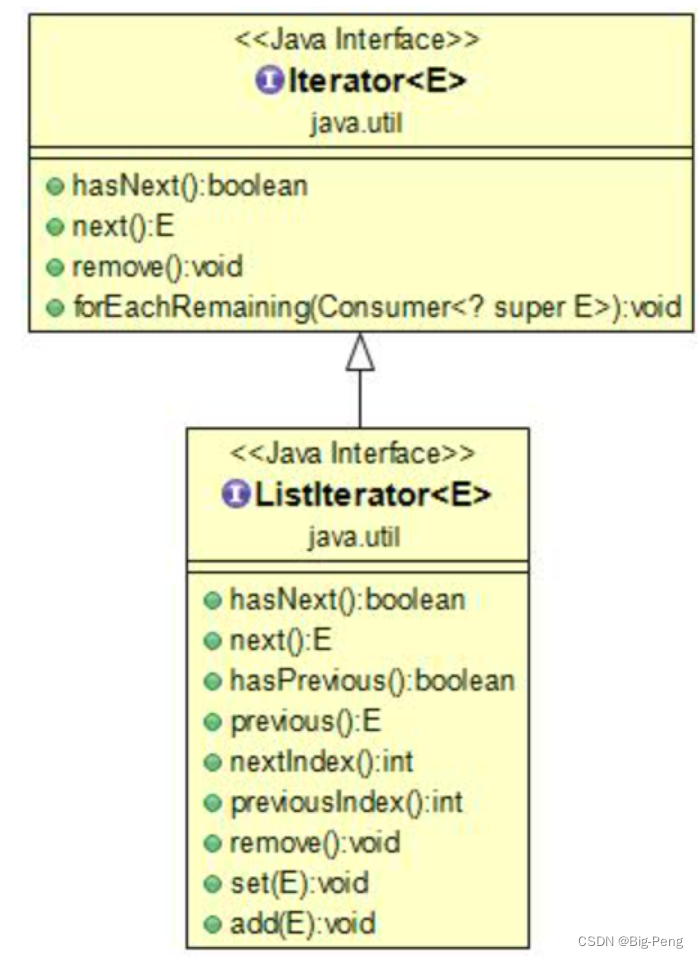
Java Iterator(迭代器)
Java迭代器(Iterator)是 Java 集合框架中的一种机制,是一种用于遍历集合(如列表、集合和映射等)的接口。 它提供了一种统一的方式来访问集合中的元素,而不需要了解底层集合的具体实现细节。 Iterator 是 …...

Logstash同步MySQL数据到ElasticSearch
当MySQL数据到一定的数量级,而且索引不能实现时,查询就会变得非常缓慢,所以使用ElasticSearch来查询数据。本篇博客介绍使用Logstash同步MySQL数据到ElasticSearch,再进行查询。 测试环境 Windows系统MySQL 5.7Logstash 7.0.1El…...

【C++】运算符重载的示例实现和应用
C运算符重载的格式: operator 运算符 比如要重载 ! 运算符 : operator ! 下面是一个例子: class DemoText{DemoText(string str, int num){m_text str; m_number num;}string m_text;int m_number; }这里来定义两个对象:…...

Kubernetes禁止调度
在Kubernetes中,您可以通过几种方式来禁止某个Pod调度到节点上。以下是一些方法: Node Selector:您可以使用Node Selector来限制Pod只能调度到带有特定标签的节点上。如果您希望完全禁止Pod调度到某些节点上,可以确保这些节点不拥…...

CocosCreator3.8研究笔记(七)CocosCreator 节点和组件的介绍
相信很多新手朋友,肯定会问,CocosCreator 中什么是节点?什么是组件? 一、什么是组件(Component)? Cocos Creator 3.8 的工作流程是以组件式开发为核心,即以组合而非继承的方式进行游…...

Ceph入门到精通-C++入门知识点
C中的双冒号(::)是作用域分解运算符(scope resolution operator)。 它主要有以下两种用法: 用于区分同名的不同成员,例如在不同类中声明了同名的成员函数或成员变量,可以使用A::B的方式来特指A类的B成员。当全局变量…...

Ansible之playbook详解和应用实例
目录 一、playbook简介 1.什么是playbook 2.playbook组成 二、应用实例 1.使用playbook安装启用httpd服务 2.使用playbook安装启用nginx服务 三、ansible-playbook其他用法 1.检查yaml文件的语法是否正确 2.检查tasks任务 3.检查指定的主机 4.指定从某个task开始运行…...

经验萃取方法
【经验萃取】 经验萃取不是简单的总结提炼归纳! 经验萃取需经过还原、复盘分析、萃取重构 一.经验萃取前三个准备 1.定主题: 萃取主题选择(阐述原因、确定级别、差距/问题是源头)->多维评分:普遍性、重要性、迫切…...

手写apply方法
<script>/** 手写apply方法 * */Function.prototype.myApply function (context, args) {console.log(this, sss)//fnconst key Symbol()context[key] thiscontext[key](...args)delete context[key]return context[key]}const obj {name: zs,age: 18}function fn …...
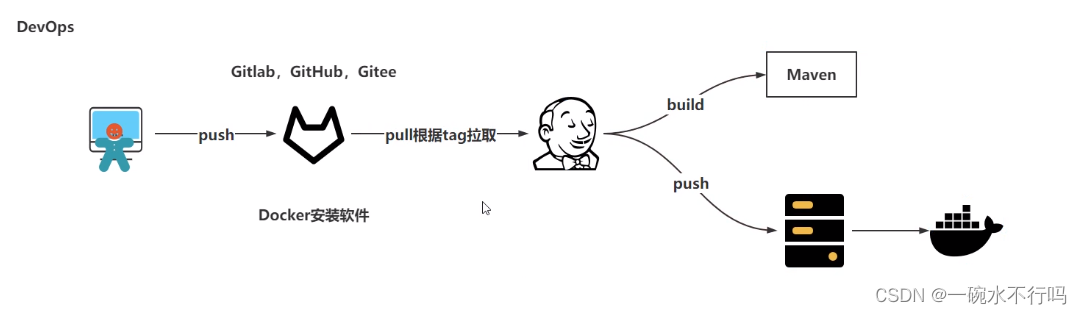
Jenkins实现基础CD操作
操作截图 在Jenkins里面设置通过标签进行构建 在Jenkins中进入项目,配置以下 将execute shell换到invoke top-level maven targets之前 在gitlab中配置标签 代码迭代新的版本 项目代码迭代 修改docker-compose.yml 提交新版本的代码 在Jenkins中追加新…...
)
开源软件合集(Docker)
Docker安装 1.安装命令:curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun2.启动:systemctl start docker3.停止:systemctl stop docker4.重启:systemctl restart docker5.开机启动:systemctl enab…...

Ceph入门到精通-生产日志级别设置
Ceph 子系统及其日志记录级别的信息。 了解 Ceph 子系统及其日志记录级别 Ceph 由多个子系统组成: 每个子系统都有其日志记录级别: 默认情况下存储在 /var/log/ceph/ 目录中的输出日志(日志级别)存储在内存缓存中的日志&#…...

16-MyCat
一 Mycat概述 1 什么是Mycat 什么是Mycat Mycat是数据库中间件,所谓数据库中间件是连接Java应用程序和数据库中间的软件。 为什么要用Mycat 遇到问题: Java与数据库的紧耦合高访问量高并发对数据库的压力读写请求数据不一致 2 Mycat与其他中间件区别 目…...
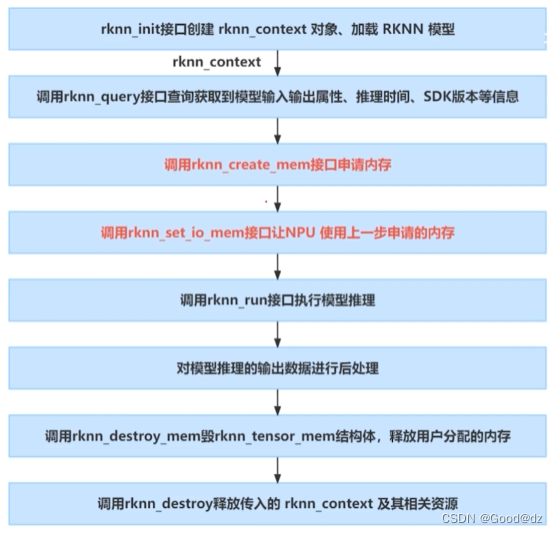
RKNPU2通用API和零拷贝API
RKNPU2通用API 通用API接口按照异构编程规范,需要将数据拷贝到NPU运行时的内存空间。 通用API部署流程 初始化上下文,需要先创建上下文对象和读取模型文件 rknn_context ctx; model load_model(model_path, &model_len); ret rknn_init(&ctx…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
