当前位置： 首页 > news >正文

论文笔记：DropMessage: Unifying Random Dropping for Graph Neural Networks

news 2026/2/11 2:47:05

（AAAI 23 优秀论文）

1 intro

  • GNN的一个普遍思路是，每一层卷积层中，从邻居处聚合信息
    • 尽管GNN有显著的进步，但是在大规模图中训练GNN会遇到各种问题：
      • 过拟合
        • 过拟合之后，GNN的泛化能力就被限制了
      • 过渡平滑
        • 经过多轮邻居信息整合的迭代之后，GNN中不同点之前的表征会很相似
      • 不够鲁棒
        • 由于需要不断迭代聚合邻居信息，所以带有噪声的图可能会影响到GNN的表现

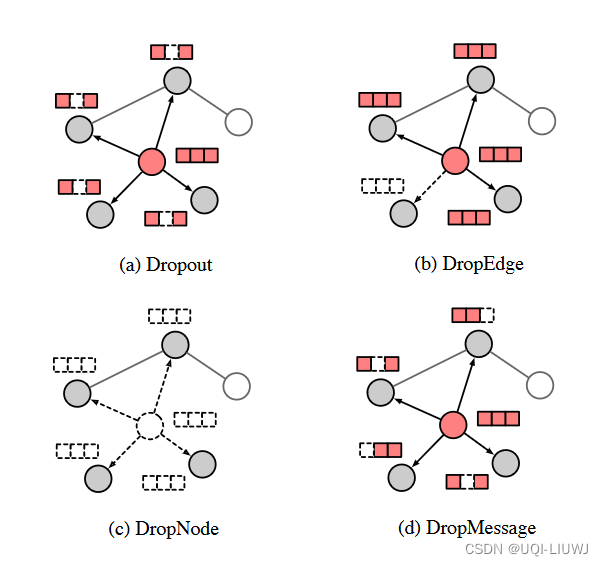
  • 上述提到的问题可以通过random dropping的方式解决
    • random dropping可以看作，通过对训练数据加噪声，缓解过拟合
    • DropOut
      • 对点的特征进行Drop out
    • DropEdge
      • 对图中的边进行drop out
    • DropNode
      • 对图中的点进行drop out
    • ——>他们都在一定程度上提升了GNN的表现
    • 但是一些开放性的问题仍然摆在random dropping问题前：
      • 引入GNN的随机噪声使得参数更难收敛，训练过程不稳定
      • 很难针对所有的图和所有的模型找到一个通用的最佳dropping方案来
      • 尚未有理论说明random dropping的有效性
  • 这篇Paper提出了一种新的random dropping方法，称之为DropMessage
    • 可以应用在所有基于信息传递的GNN中
    • 在消息矩阵上进行drop操作
      • ——>可以让同一个点向不同的邻居传递不同的消息
    • 将现有的random dropping方法整合到DropMessage中
    • 从理论层面证明了在GNN中添加random dropping，等价于提供了一个额外的正则项
    • 从信息论的角度，DropMessage保留了最多的信息多样性、是其他random dropping方法的上界

 2 Notation & Preliminary

2.1 记号

  • G=(V,E)表示图
    • \mathbf{V}=\left\{v_1, \ldots, v_n\right\}表示点集
    • E是边集
  • 节点特征矩阵为\mathbf{X}=\left\{x_1, \ldots, x_n\right\} \in \mathbb{R}^{n \times c}
  • 邻接矩阵是\mathbf{A}=\left\{a_1, \ldots, a_n\right\} \in \mathbb{R}^{n \times n}，Aij表示点vi和点vj之间的邻接关系
  • 每个点的度是\mathbf{d}=\left\{d_1, \ldots, d_n\right\}
    • 图的度是\mathbf{d}(\mathbf{G})=\sum_i^n d_i
  • 我们有k条边（有向边），那么信息传递矩阵为\mathbf{M}=\left\{m_1, \ldots, m_k\right\} \in \mathbb{R}^{k \times c}
    • 每一行表示一条边上传递的信息

 2.2 GNN

  • message passing的GNN可以表示为
    • h_i^{(l+1)}=\gamma^{(l)}\left(h_i^{(l)}, \mathcal{A G G}_{j \in \mathcal{N}(i)}\left(\phi^{(l)}\left(h_i^{(l)}, h_j^{(l)}, e_{j, i}\right)\right)\right)
      • h_i^{(l)}表示第l层点vi的表征
      • N(i)是点vi的邻居
      • ej,i是点j到i的边
      • \phi^{(l)},\gamma^{(l)}是可微函数
      • AGG是一种聚合函数（比如SUM，MEAN等）
  • 记\mathbf{K}^{(l)} \in \mathbb{R}^{k \times n}为一个one-hot编码（每一行表示是这条边是由哪个点射出的）
    • 信息传递矩阵M可以表示为\mathbf{M}^{(l)}=\mathbf{K}^{(l)} \mathbf{H}^{(l)}

3 DropMessage

3.1 方法介绍

  • 在信息传递矩阵M上进行drop操作
  • 记dropping rate为δ，那么δ|M|个M上的元素将会被mask掉
  • 记一个伯努利分布\epsilon_{i, j} \sim \text { Bernoulli }(1-\delta)
    • 那么drop之后的信息传递矩阵为\widetilde{\mathbf{M}}_{i, j}=\epsilon \mathbf{M}_{i, j}（分布为1的保留，所以伯努利分布的p为1-δ）
    • 为了让drop之后的信息传递矩阵的期望和drop之前的期望一致，对drop之后的信息传递矩阵乘以一个系数\widetilde{\mathbf{M}}_{i, j}=\frac{1}{1-\delta} \epsilon_{i, j} \mathbf{M}_{i, j}

3.2 整合之前的random dropping方法

之前的几种random dropping，都可以看作是DropMessage的特例

3.3 理论部分

  • GNN上的无偏随机丢弃，可以看成是给目标函数添加了一个额外的正则项，这可以使得模型更鲁棒

3.4 DropMessage的好处

  • 减少样本方差
    • 随机丢弃会在训练过程中引入噪声，使得训练过程不稳定
    • 在给定丢弃率δ的情况下，DropMessage有最小的样本方差
  • 定义信息多样性
    • 包括特征多样性和拓扑多样性
      • 特征多样性指从不同点中保留的特征维数的数量（就是有多少个特征没有被完全丢弃掉）
      • 拓扑多样性指多少条有向边上有信息传递
    • Dropout、DropEdge、DropNode都不能保持信息多样性，但是DropMessage可以

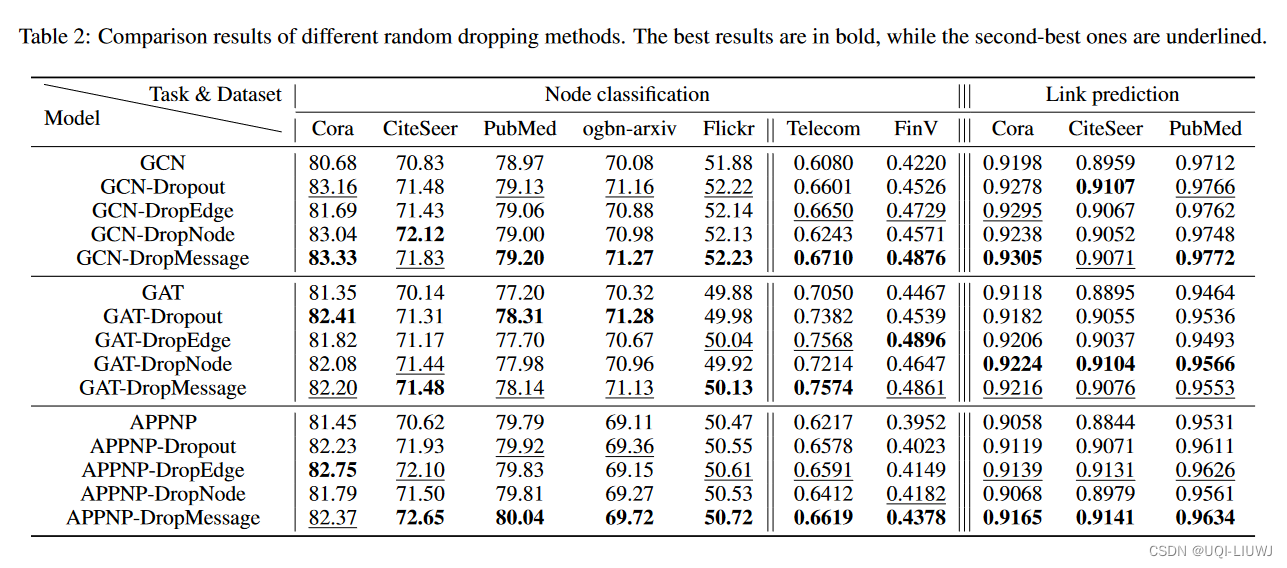
4 实验

 

 

相关文章：

论文笔记：DropMessage: Unifying Random Dropping for Graph Neural Networks

（AAAI 23 优秀论文） 1 intro GNN的一个普遍思路是，每一层卷积层中，从邻居处聚合信息 尽管GNN有显著的进步，但是在大规模图中训练GNN会遇到各种问题： 过拟合 过拟合之后，GNN的泛化能力就被限制…...

编程日记 2023/2/22 10:16:15

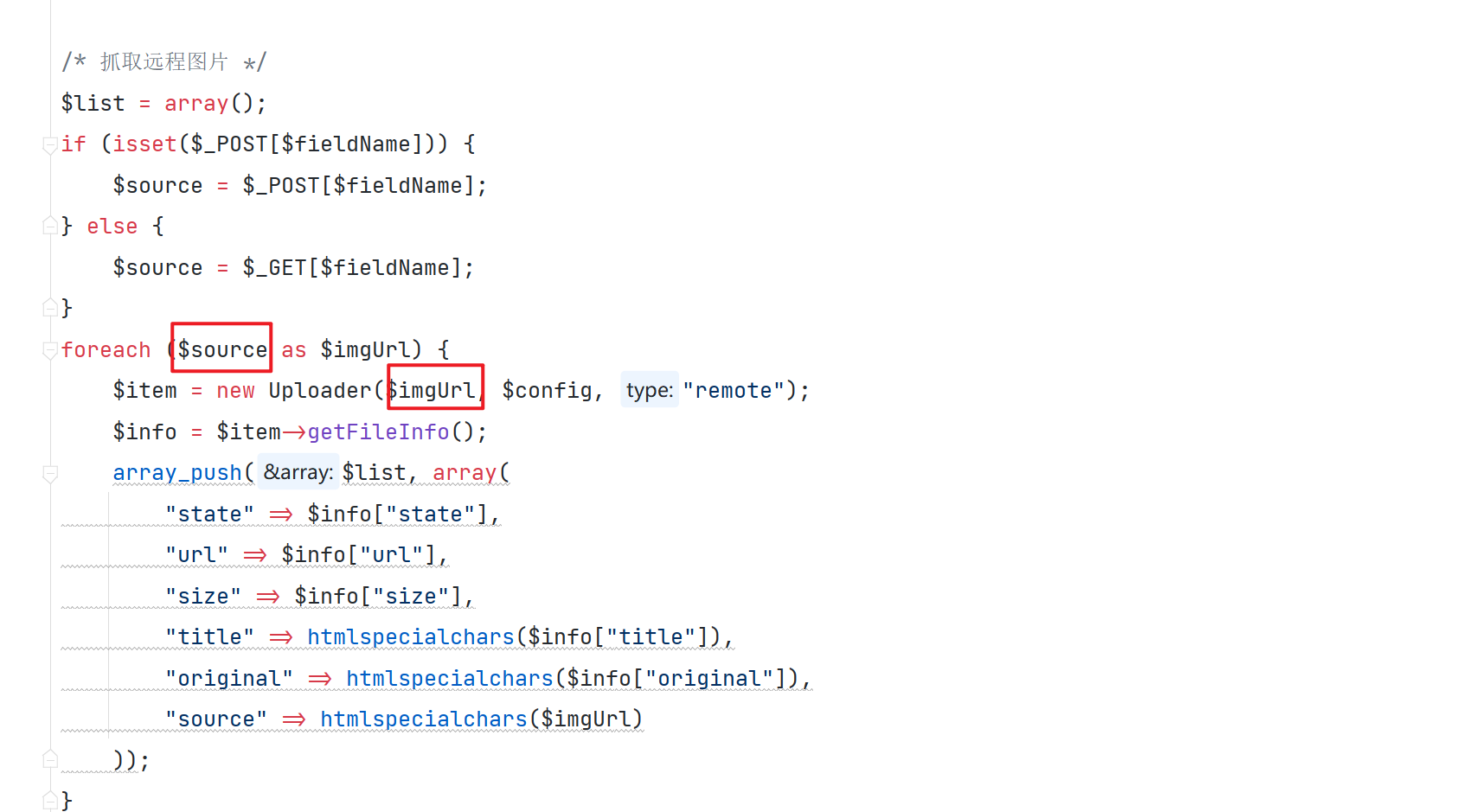
木鱼cms系统审计小结

MuYuCMS基于Thinkphp开发的一套轻量级开源内容管理系统,专注为公司企业、个人站长提供快速建站提供解决方案。 ​​ ‍ 环境搭建 我们利用 phpstudy 来搭建环境，选择 Apache2.4.39 MySQL5.7.26 php5.6.9 ，同时利用 PhpStorm 来实现对项目的调试 ​…...

编程日记 2023/2/22 10:15:06

软件测试面试-一线大厂必问的测试思维面试题

五、测试思维5.1 打电话功能怎么去测？我们会从几个方面去测试：界面、功能、兼容性、易用性、安全、性能、异常。1）界面我们会测试下是否跟界面原型图一致，考虑浏览器不同显示比例，屏幕分辨率。2）功能&#…...

编程日记 2023/2/22 10:14:00

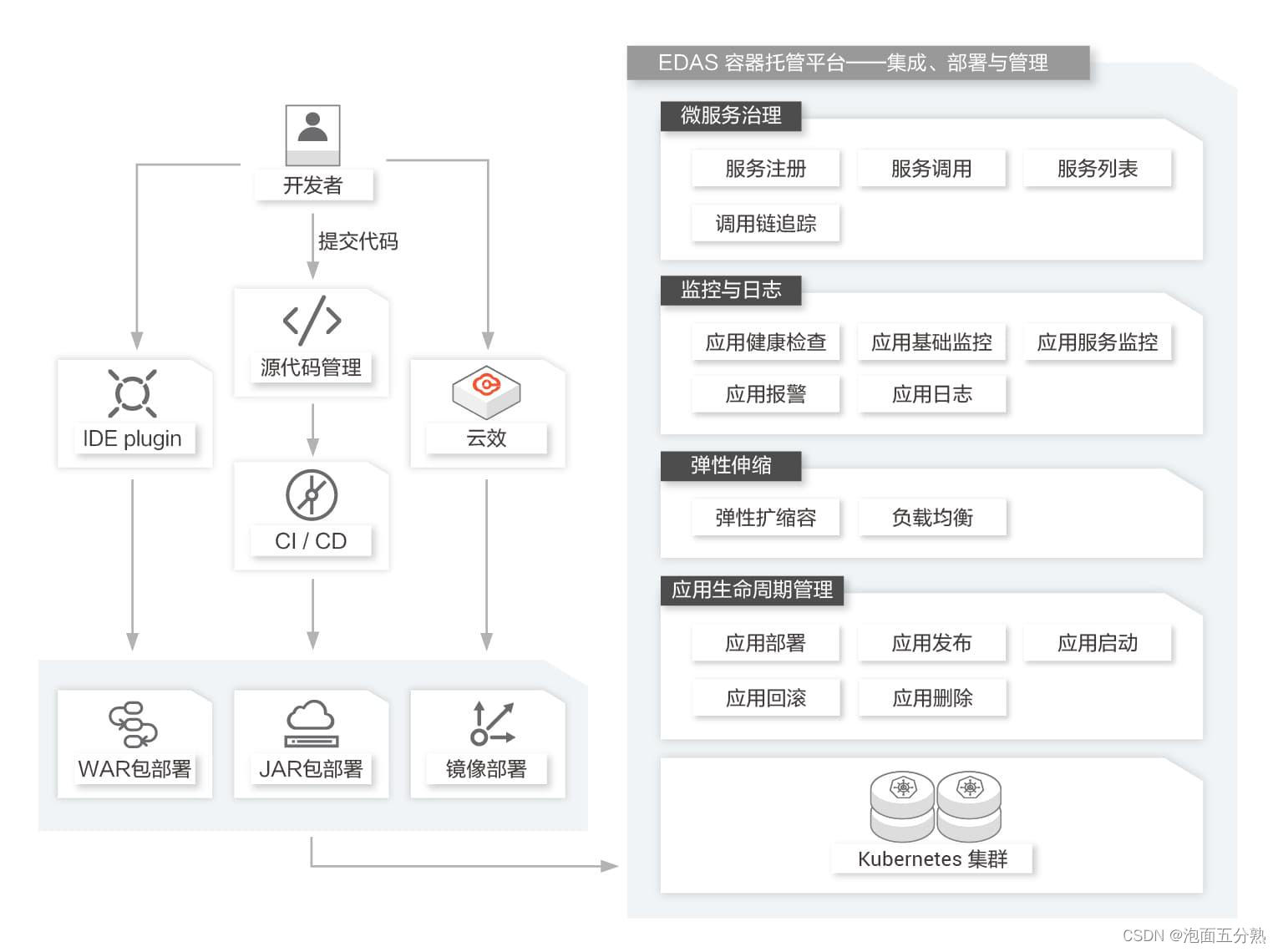
企业级分布式应用服务 EDAS

什么是企业级分布式应用服务EDAS企业级分布式应用服务EDAS（Enterprise Distributed Application Service）是一个应用托管和微服务管理的云原生PaaS平台，提供应用开发、部署、监控、运维等全栈式解决方案，同时支持Spring Cloud和Ap…...

编程日记 2023/2/22 10:12:53

弄懂 Websocket 你得知道的这 3 点

1. WebSocket原理 WebSocket同HTTP一样也是应用层的协议，但是它是一种双向通信协议，是建立在TCP之上的。 WebSocket是一种在单个TCP连接上进行全双工通信的协议。WebSocket API也被W3C定为标准。 WebSocket使得客户端和服务器之间的数据交换变得更加简…...

编程日记 2023/2/22 10:11:49

Appium构架及工作原理

一、appium结构简单来说appium充当一个中间服务器的功能，接收来自我们代码的请求，然后发送到手机上进行执行。二、初步认识appium工作过程1.appium是c/s模式的2.appium是基于webdriver协议添加对移动设备自动化api扩展而成的，所以具有和webdr…...

编程日记 2023/2/22 10:10:40

软件架构中“弹性”的多种含义

在软件架构领域的中文文档、书籍中，经常可以看到“弹性”这个专业术语，但在不同的语境下含义可能会不同。 在英语中，elastic 和 resilient 两个单词都可以翻译为“弹性的”，但是它们在软件架构中代表的含义却完全不同&#xff0c…...

编程日记 2023/2/22 10:08:25

JAVA练习57- 罗马数字转整数、位1的个数

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 目录 前言 一、题目1-罗马数字转整数 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 二、题目2-位1的个数 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 …...

编程日记 2023/2/22 10:07:20

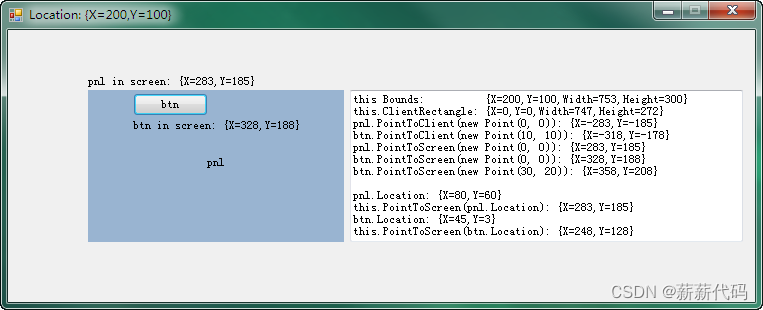
C#把图片放到picturebox上的指定位置，PointToClient与PointToScreen解读

1、C#中如何把图片放到picturebox上的指定位置 构造一个跟picturebox1一样大小的Bitmap， 设置给picturebox1， 然后在上面画图 Bitmap image new Bitmap(picturebox1.Size.Width, picturebox1.Size.Height); Graphics device Graphics.FromImage(imag…...

编程日记 2023/2/22 10:06:11

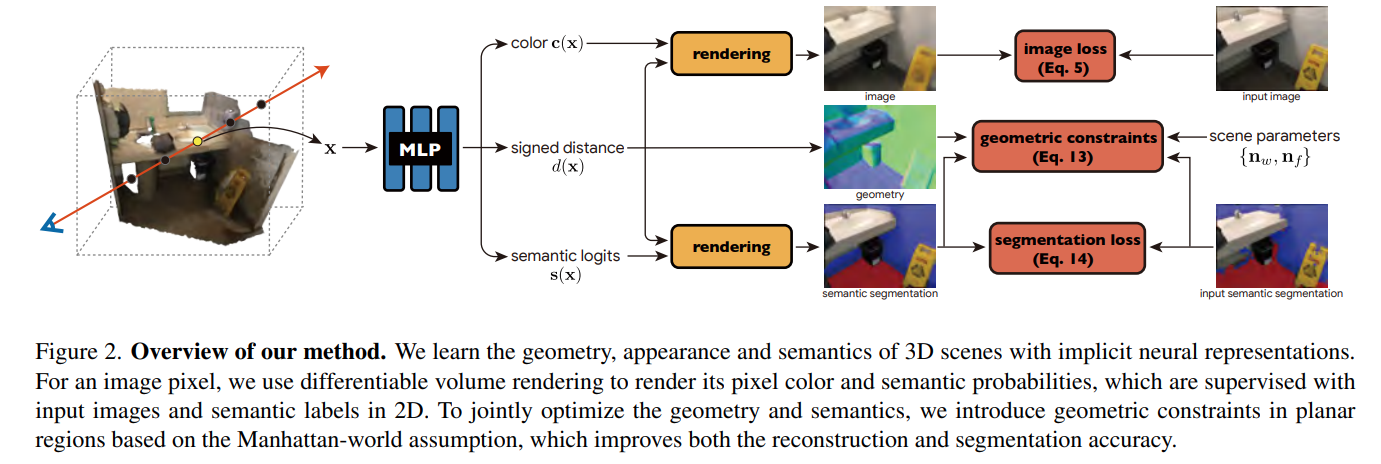
【论文笔记】Manhattan-SDF==ZJU==CVPR‘2022 Oral

Neural 3D Scene Reconstruction with the Manhattan-world Assumption 本文工作：基于曼哈顿世界假设，重建室内场景三维模型。 1.1 曼哈顿世界假设 参考阅读文献：Structure-SLAM: Low-Drift Monocular SLAM in Indoor EnvironmentsIEEE IR…...

编程日记 2023/2/22 10:05:04

环翠区中小学生编程挑战赛题解中学组T4：免费超市

题目描述 OITV电视台最近开设了名为“免费超市”的真人电视节目，在节目中，抽奖选拔的民间志愿者们将随机匹配进行两两对抗赛。每场比赛上，节目组设置 n n n件商品排成一排供选手挑选，两名选手将交替出手选中并拿走商品，每件商品有着不同的价值 a i a_i a...

编程日记 2023/2/22 10:03:57

关于Oracle树形查询（connect by）的学习笔记

1.查找员工 FORD的上级 Note：在查找时，应当注意树形是倒过来的。（自下而上），故此父亲节点是MGR ，而儿子节点是EMPNO –PRIOR MGREMPNO也是可以的。 以下两种方式均可以实现查找FORD的上级。 SQL> SQ…...

编程日记 2023/2/22 10:02:46

观看课程领奖品！Imagination中国区技术总监全面解读 IMG DXT GPU

此前，我们发布了一系列关于 IMG DXT GPU 的介绍，为了让更多读者了解其背后的技术及应用方向，我们特别邀请 Imagination 中国区技术总监艾克录制全新在线课程，为大家全面解读IMG DXT GPU。 点击这里，马上注册观看&…...

编程日记 2023/2/22 10:01:40

To_Heart—题解——[SCOI2012]奇怪的游戏

题意 link. 给定一个 nmn\times mnm 的棋盘，每次操作可以选择两个相邻的格子，让这两个各自上的数都 1。问最少多少次操作使得所有格子的数相等。如果永远不行则输出-1。 题解 因为相邻两个格子进行操作，而且是方格，所以很容易…...

编程日记 2023/2/22 10:00:34

Spring Boot Hello World 基于 IDEA 案例详解

一、Spring Boot 是什么 世界上最好的文档来源自官方的《Spring Boot Reference Guide》，是这样介绍的： Spring Boot makes it easy to create stand-alone, production-grade Spring based Applications that you can “just run”...Most Spring Boot…...

编程日记 2023/2/22 9:59:28

基于机器学习的异常检测与分析技术

传统的运维方式在监控、问题发现、告警以及故障处理等各个环节均存在明显不足，需要大量依赖人的经验，在数据采集、异常诊断分析、故障处理的效率等方面有待提高。 本关键技术面对传统运维故障处理效率低、问题定位不准确、人力成本高三大痛点&#xff0…...

编程日记 2023/2/22 9:57:14

pytest进阶之html测试报告

pytest进阶之html测试报告 目录：导读 前言 pytest-html生成报告 安装 生成报告 效果 错误用例截图 添加描述 小结 allure2生成报告 安装allure 安装pytest-allure-adaptor插件 生成xml格式报告 添加环境变量 运行allure生成报告 效果 总结 前言 …...

编程日记 2023/2/22 9:56:09

劳特巴赫仿真测试工具Trace32的基本使用（cmm文件）

劳特巴赫 Trace32 调试使用教程 使用PRACTICE 脚本(.cmm) 在TRACE32 中使用PRACTICE 脚本(*.cmm)将帮助你： 在调试器启动时立即执行命令根据您的项目需求自定义TRACE32PowerView用户界面加载应用程序或符号使调试操作具有可重复性， 并可用于验证目的和回归测试 自动启动脚本…...

编程日记 2023/2/22 9:55:02

盘点四种自动化测试模型实例及优缺点

一，线性测试 1.概念： 通过录制或编写对应应用程序的操作步骤产生的线性脚本。单纯的来模拟用户完整的操作场景。 （操作，重复操作，数据）都混合在一起。 2.优点： 每个脚本相对独立&#xff0…...

编程日记 2023/2/22 9:53:53

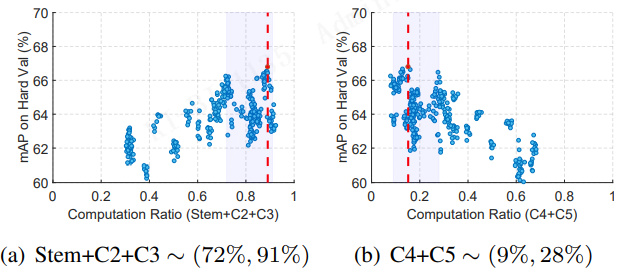
【论文阅读】SCRFD: Sample and Computation 重分配的高效人脸检测

原始题目Sample and Computation Redistribution for Efficient Face Detection中文名称采样和计算 重分配的 高效人脸检测发表时间2021年5月10日平台ICLR-2022来源Imperial College， InsightFace文章链接https://arxiv.org/pdf/2105.04714.pdf开源代码官方实现&…...

编程日记 2023/2/22 9:52:47

【Axure高保真原型】引导弹窗

今天和大家中分享引导弹窗的原型模板，载入页面后，会显示引导弹窗，适用于引导用户使用页面，点击完成后，会显示下一个引导弹窗，直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

编程新知 2026/2/10 22:45:42

C++初阶-list的底层

目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

编程新知 2026/2/8 20:42:41

Zustand 状态管理库：极简而强大的解决方案

Zustand 是一个轻量级、快速和可扩展的状态管理库，特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

编程新知 2026/2/8 10:56:57

阿里云ACP云计算备考笔记 (5)——弹性伸缩

目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

编程新知 2026/1/22 6:07:24

1688商品列表API与其他数据源的对接思路

将1688商品列表API与其他数据源对接时，需结合业务场景设计数据流转链路，重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点： 一、核心对接场景与目标 商品数据同步 场景：将1688商品信息…...

编程新知 2025/11/30 16:55:32

江苏艾立泰跨国资源接力：废料变黄金的绿色供应链革命

在华东塑料包装行业面临限塑令深度调整的背景下，江苏艾立泰以一场跨国资源接力的创新实践，重新定义了绿色供应链的边界。 跨国回收网络：废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点，将海外废弃包装箱通过标准…...

编程新知 2026/1/31 13:42:15

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程：首先由HR先筛选一部分简历后，在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如：Boss直聘（招聘方平台） 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2026/1/26 19:10:48

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2026/2/6 2:05:50

有限自动机到正规文法转换器v1.0

1 项目简介 这是一个功能强大的有限自动机&#xff08;Finite Automaton, FA&#xff09;到正规文法&#xff08;Regular Grammar&#xff09;转换器&#xff0c;它配备了一个直观且完整的图形用户界面&#xff0c;使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

编程新知 2026/1/31 13:13:32

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18