JAVA练习57- 罗马数字转整数、位1的个数
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
目录
前言
一、题目1-罗马数字转整数
1.题目描述
2.思路与代码
2.1 思路
2.2 代码
二、题目2-位1的个数
1.题目描述
2.思路与代码
2.1 思路
2.2 代码
总结
前言
提示:这里可以添加本文要记录的大概内容:
2月21日练习内容
提示:以下是本篇文章正文内容,下面案例可供参考
一、题目1-罗马数字转整数
1.题目描述
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。示例 1:
输入: s = "III"
输出: 3
示例 2:
输入: s = "IV"
输出: 4
示例 3:
输入: s = "IX"
输出: 9
示例 4:
输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/roman-to-integer
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
2.思路与代码
2.1 思路
1.创建一个方法,用来获取字符串中某个字符所对应的值
2.创建两个变量,一个是数的和sum,另一个是前一个字符所对应的值pre
3.for循环,索引i从1开始,到字符串的长度s.length()-1结束,
4.获取当前i字符所对应的值,用它与上一个字符的值比较,若该字符的值比上一个字符的值大,则sum -= pre;若小,则sum += pre;接着更新pre = num(当前i值)进入下一次循环
5.最后将最后一个元素的值与sum相加,输出sum即可
2.2 代码
代码如下(示例):
class Solution {public int romanToInt(String s) {//和int sum = 0;//上一个字符所对应的值int pre = getValue(s.charAt(0));//遍历字符串取值for(int i = 1;i < s.length();i ++){//当前i处的值int num = getValue(s.charAt(i));//如果上一个字符所对应的值比当前i处字符所对应的值小if(pre < num){sum -= pre;}else{sum += pre;}//更新prepre = num;}//将最后一个字符元素所对应的值加入sumsum += pre;return sum;}//获取对应字符的值private int getValue(char ch){switch(ch){case 'I':return 1;case 'V':return 5;case 'X':return 10;case 'L':return 50;case 'C':return 100;case 'D':return 500;case 'M':return 1000;default:return 0;}}
}二、题目2-位1的个数
1.题目描述
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 3 中,输入表示有符号整数 -3。
示例 1:
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:n = 00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:n = 11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/number-of-1-bits
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
2.思路与代码
2.1 思路
1.while循环遍历,
2.count += n & 1;将n的最后一位加给count,如果最后一位是1,则count+1,如果不是1,因为该数字是二进制,所以count+0,数字无变化
3。接着将数字进行无符号右移
4.输出count
2.2 代码
代码如下(示例):
public class Solution {// you need to treat n as an unsigned valuepublic int hammingWeight(int n) {//计数器int count = 0;while(n != 0){//n&1是获取n的最右一位count += n & 1;//n>>>1是无符号右移n = n >>> 1;}return count;}
}总结
提示:这里对文章进行总结:
相关文章:

JAVA练习57- 罗马数字转整数、位1的个数
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目1-罗马数字转整数 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 二、题目2-位1的个数 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 …...
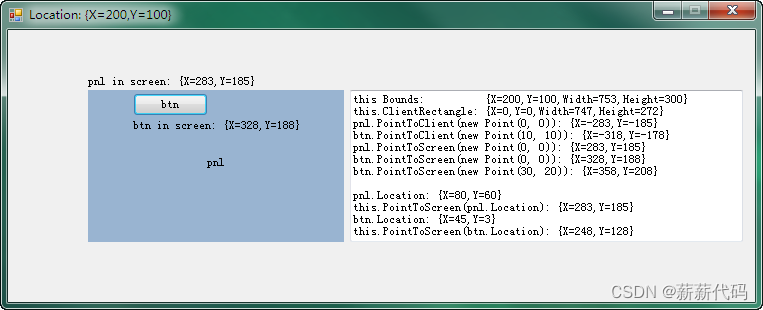
C#把图片放到picturebox上的指定位置,PointToClient与PointToScreen解读
1、C#中如何把图片放到picturebox上的指定位置 构造一个跟picturebox1一样大小的Bitmap, 设置给picturebox1, 然后在上面画图 Bitmap image new Bitmap(picturebox1.Size.Width, picturebox1.Size.Height); Graphics device Graphics.FromImage(imag…...
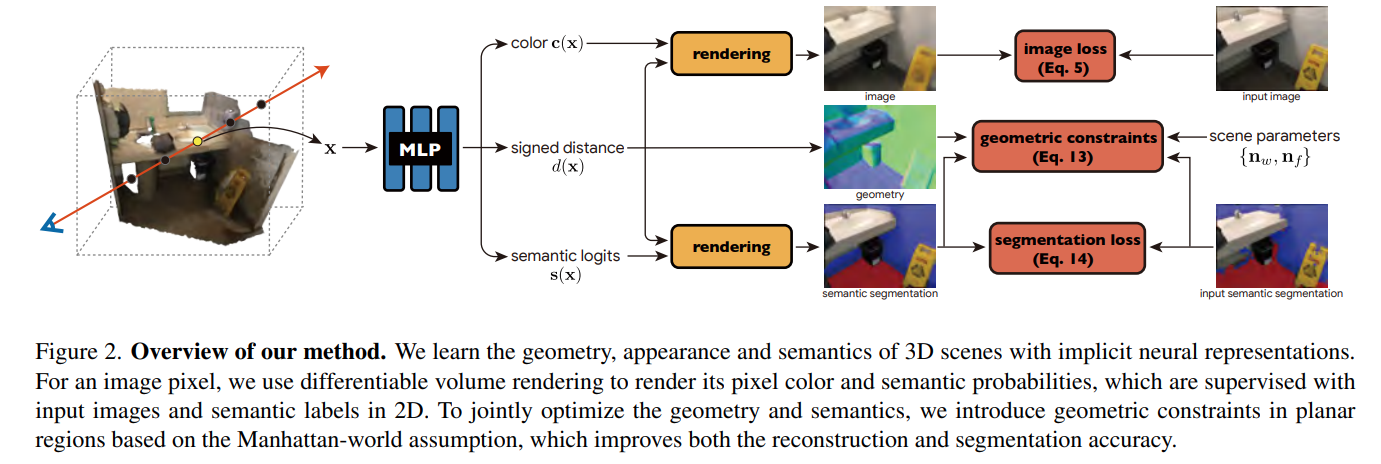
【论文笔记】Manhattan-SDF==ZJU==CVPR‘2022 Oral
Neural 3D Scene Reconstruction with the Manhattan-world Assumption 本文工作:基于曼哈顿世界假设,重建室内场景三维模型。 1.1 曼哈顿世界假设 参考阅读文献:Structure-SLAM: Low-Drift Monocular SLAM in Indoor EnvironmentsIEEE IR…...

环翠区中小学生编程挑战赛题解中学组T4:免费超市
题目描述 OITV电视台最近开设了名为“免费超市”的真人电视节目,在节目中,抽奖选拔的民间志愿者们将随机匹配进行两两对抗赛。每场比赛上,节目组设置 n n n件商品排成一排供选手挑选,两名选手将交替出手选中并拿走商品,每件商品有着不同的价值 a i a_i a...
的学习笔记)
关于Oracle树形查询(connect by)的学习笔记
1.查找员工 FORD的上级 Note:在查找时,应当注意树形是倒过来的。(自下而上),故此父亲节点是MGR ,而儿子节点是EMPNO –PRIOR MGREMPNO也是可以的。 以下两种方式均可以实现查找FORD的上级。 SQL> SQ…...

观看课程领奖品!Imagination中国区技术总监全面解读 IMG DXT GPU
此前,我们发布了一系列关于 IMG DXT GPU 的介绍,为了让更多读者了解其背后的技术及应用方向,我们特别邀请 Imagination 中国区技术总监艾克录制全新在线课程,为大家全面解读IMG DXT GPU。 点击这里,马上注册观看&…...

To_Heart—题解——[SCOI2012]奇怪的游戏
题意 link. 给定一个 nmn\times mnm 的棋盘,每次操作可以选择两个相邻的格子,让这两个各自上的数都 1。问最少多少次操作使得所有格子的数相等。如果永远不行则输出-1。 题解 因为相邻两个格子进行操作,而且是方格,所以很容易…...

Spring Boot Hello World 基于 IDEA 案例详解
一、Spring Boot 是什么 世界上最好的文档来源自官方的《Spring Boot Reference Guide》,是这样介绍的: Spring Boot makes it easy to create stand-alone, production-grade Spring based Applications that you can “just run”...Most Spring Boot…...
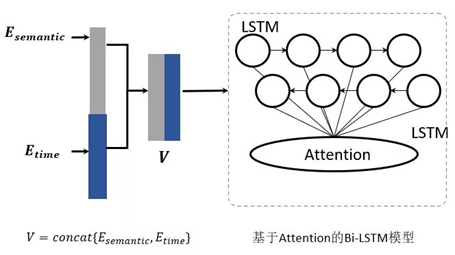
基于机器学习的异常检测与分析技术
传统的运维方式在监控、问题发现、告警以及故障处理等各个环节均存在明显不足,需要大量依赖人的经验,在数据采集、异常诊断分析、故障处理的效率等方面有待提高。 本关键技术面对传统运维故障处理效率低、问题定位不准确、人力成本高三大痛点࿰…...

pytest进阶之html测试报告
pytest进阶之html测试报告 目录:导读 前言 pytest-html生成报告 安装 生成报告 效果 错误用例截图 添加描述 小结 allure2生成报告 安装allure 安装pytest-allure-adaptor插件 生成xml格式报告 添加环境变量 运行allure生成报告 效果 总结 前言 …...

劳特巴赫仿真测试工具Trace32的基本使用(cmm文件)
劳特巴赫 Trace32 调试使用教程 使用PRACTICE 脚本(.cmm) 在TRACE32 中使用PRACTICE 脚本(*.cmm)将帮助你: 在调试器启动时立即执行命令根据您的项目需求自定义TRACE32PowerView用户界面加载应用程序或符号使调试操作具有可重复性, 并可用于验证目的和回归测试 自动启动脚本…...
盘点四种自动化测试模型实例及优缺点
一,线性测试 1.概念: 通过录制或编写对应应用程序的操作步骤产生的线性脚本。单纯的来模拟用户完整的操作场景。 (操作,重复操作,数据)都混合在一起。 2.优点: 每个脚本相对独立࿰…...
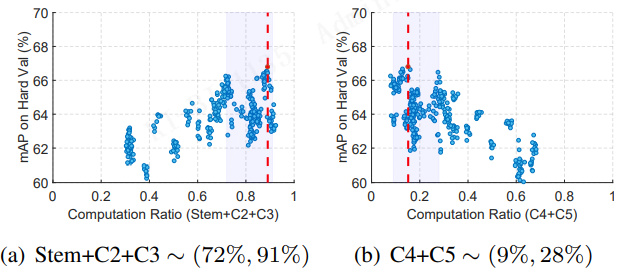
【论文阅读】SCRFD: Sample and Computation 重分配的高效人脸检测
原始题目Sample and Computation Redistribution for Efficient Face Detection中文名称采样和计算 重分配的 高效人脸检测发表时间2021年5月10日平台ICLR-2022来源Imperial College, InsightFace文章链接https://arxiv.org/pdf/2105.04714.pdf开源代码官方实现&…...

Debezium报错处理系列之四十七:Read only connection requires GTID_MODE to be ON
Debezium报错处理系列之四十七:Caused by: java.lang.UnsupportedOperationException: Read only connection requires GTID_MODE to be ON 一、完整报错二、错误原因三、错误解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make…...
类型数据类型的精度的学习)
关于float(b)类型数据类型的精度的学习
Questions: 将表中的某字段类型设计成float(2)后,向其插入数据93.5后,最好结果却变成了90?这是为什么? 关于这个问题 官方帮助文档(Oracle Online Help )的说明如下: FLOAT(b) specifies a floa…...

哪种类型的网络安全风险需要进行渗透测试?
网络在给我们带来无限方便的同时,也隐藏着无数危机。2022年网络攻击造成的损失创下新的历史记录,根据Cybersecurity Ventures最新发布的“2022年网络犯罪报告”,预计2023年网络犯罪将给全世界造成8万亿美元的损失。同时在市场和以网络安全法为…...
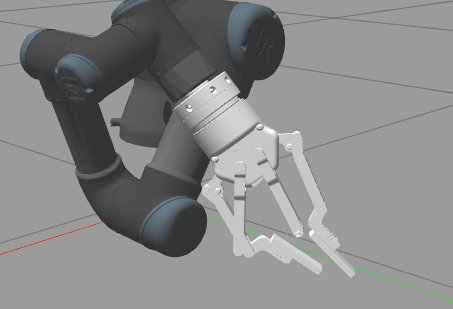
ur3+robotiq ft sensor+robotiq 2f 140配置gazebo仿真环境
ur3robotiq ft sensorrobotiq 2f 140配置gazebo仿真环境 搭建环境: ubuntu: 20.04 ros: Nonetic sensor: robotiq_ft300 gripper: robotiq_2f_140_gripper UR: UR3 通过上一篇博客配置好ur3、力传感器和robotiq夹爪的rviz仿真环境后,现在来配置一下对…...

Vue3后台管理系统(四)SVG图标
目录 一、安装 vite-plugin-svg-icons 二、创建图标文件夹 三、main.ts 引入注册脚本 四、vite.config.ts 插件配置 五、TypeScript支持 六、组件封装 七、使用 Element Plus 图标库往往满足不了实际开发需求,可以引用和使用第三方例如 iconfont 的图标&…...
)
【收集】2023年顶会accepted papers list(NeurIPS/CVPR/ICML/ICLR/ECCV/AAAI/IJCAI/WWW...)
from: https://blog.csdn.net/lijinde07/article/details/128024833 顺便看看 评审意见是怎样的 Accepted papers list(2022.11.24) AAAI 2023 :录取结果已出 **ICLR 2023 ** :https://openreview.net/group?idICLR…...

空闲态LTE到NR重选优先级介绍
SIB24消息包含小区重选时5G邻区信息(NR neighbor cell information for cell reselection)。 终端注册在LTE网络,如果网络不上报SIB24消息,则终端不会重选到5G网络。 针对这种网络不上报SIB24的场景,终端可以做特殊处理,强制执行LTE到5G的重选流程。 终端网络制式设置为不…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
