【LeetCode】剑指 Offer 10- I. 斐波那契数列 p74 -- Java Version
题目链接:
1. 题目介绍()
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
- F(0) = 0, F(1) = 1
- F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
【测试用例】:
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
【条件约束】:
提示:
- 0 <= n <= 100
2. 题解
2.1 递归实现 — O(2n)
时间复杂度O(2n),空间复杂度O(1)
class Solution {// 第一种方法:递归实现public int fib(int n) {// 1. n为0时,返回0if (n == 0) return 0;// 2. n为1时,返回1else if (n == 1) return 1;// 3. 从第三个数开始,之后的每个数都为前两项数的和else return fib(n-1) + fib(n-2);}
}

改进: 使用数组保存每一次的运算结果;改进之后时间复杂度: 从2的n次方降为了O(n²),空间复杂度:O(n)。
class Solution {int[] ints;public int fib(int n) {ints = new int[n];if(n <= 1) return n;return (f(n - 1) + f(n - 2)) % 1000000007;}private int f(int n) {if(n == 0 || n == 1) return n;if (ints[n] != 0){return ints[n];}ints[n] = (f(n - 1) + f(n - 2)) % 1000000007;return (f(n - 1) + f(n - 2)) % 1000000007;}
}
2.2 滚动数组循环实现
时间复杂度O(n),空间复杂度O(1)

数组不断滚动向后,逐次累加
class Solution {// 第二种方法:循环实现public int fib(int n) {final int MOD = 1000000007;// 1. 定义辅助数组res,用以记录当前值的前两项值long[] res = {0,1};// 2. 如果n小于2,直接返回if (n < 2){return (int)res[n];} // 3. 定义sum,用于记录从第三项开始,所得到的前两项加和long sum = 0;for (int i = 2; i <= n; i++){ // 4. sum为前两项加和,然后依次交换元素,逐次相加sum = (res[0] + res[1]) % MOD;res[0] = res[1];res[1] = sum;}return (int)sum;}
}
2.3 矩阵快速幂 – O(logn)
时间复杂度O(logn),空间复杂度O(1)

这就涉及到了斐波那契数列的数学公式。
快速幂算法原理: 如需求数据 a 的幂次,此处 a 可以为数也可以为矩阵,常规做法需要对a进行不断的乘积即 a * a * a * …
以求 3^10 的结果为例:
[优化步骤1:]
易知:
3^10=3*3*3*3*3*3*3*3*3*3
=9^5 = 9^4*9
=81^2*9
=6561*9
基于以上原理,我们在计算一个数的多次幂时,可以先判断其幂次的奇偶性,然后:
-
如果幂次为偶直接 base(底数) 作平方,power(幂次) 除以2
-
如果幂次为奇则底数平方,幂次整除于2然后再多乘一次底数
[优化步骤2:]
对于以上涉及到 [判断奇偶性] 和 [除以2] 这样的操作。使用系统的位运算比普通运算的效率是高的,因此可以进一步优化:
-
把 power % 2 == 1 变为 (power & 1) == 1
-
把 power = power / 2 变为 power = power >> 1
class Solution {static final int MOD = 1000000007;public int fib(int n) {//矩阵快速幂if (n < 2) {return n;}//定义乘积底数int[][] base = {{1, 1}, {1, 0}};//定义幂次int power = n - 1;int[][] ans = calc(base, power);//按照公式,返回的是两行一列矩阵的第一个数return ans[0][0];}//定义函数,求底数为 base 幂次为 power 的结果public int[][] calc(int[][] base, int power) {//定义变量,存储计算结果,此次定义为单位阵int[][] res = {{1, 0}, {0, 1}};//可以一直对幂次进行整除while (power > 0) {//1.若为奇数,需多乘一次 base//2.若power除到1,乘积后得到res//此处使用位运算在于效率高if ((power & 1) == 1) {res = mul(res, base);}//不管幂次是奇还是偶,整除的结果是一样的如 5/2 和 4/2//此处使用位运算在于效率高power = power >> 1;base = mul(base, base);}return res;}//定义函数,求二维矩阵:两矩阵 a, b 的乘积public int[][] mul(int[][] a, int[][] b) {int[][] c = new int[2][2];for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {//矩阵乘积对应关系,自己举例演算一遍便可找到规律c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);}}return c;}
}
3. 参考资料
[1] 一题解带你走进递归和动态规划算法的大门 – 递归改进代码来源
[2] 斐波那契数列(力扣官方题解)-- (Comment 腌菜读作梦想) – 矩阵快速幂解法来源
相关文章:

【LeetCode】剑指 Offer 10- I. 斐波那契数列 p74 -- Java Version
题目链接: 1. 题目介绍() 写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下: F(0) 0, F(1) 1F(N) F(N - 1) F…...
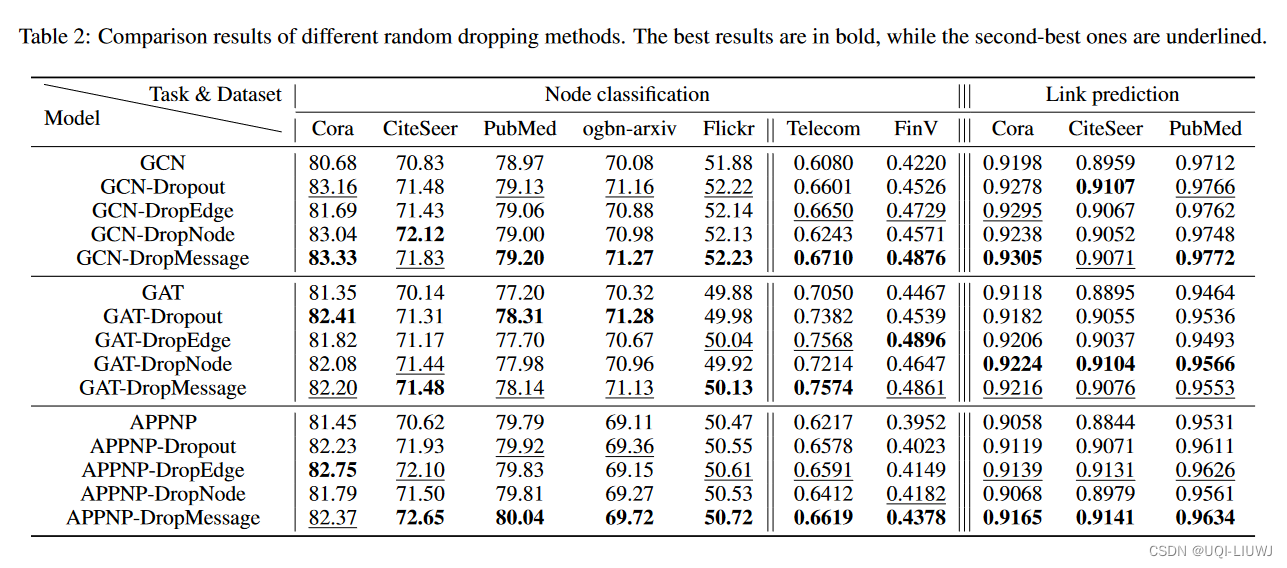
论文笔记:DropMessage: Unifying Random Dropping for Graph Neural Networks
(AAAI 23 优秀论文) 1 intro GNN的一个普遍思路是,每一层卷积层中,从邻居处聚合信息 尽管GNN有显著的进步,但是在大规模图中训练GNN会遇到各种问题: 过拟合 过拟合之后,GNN的泛化能力就被限制…...
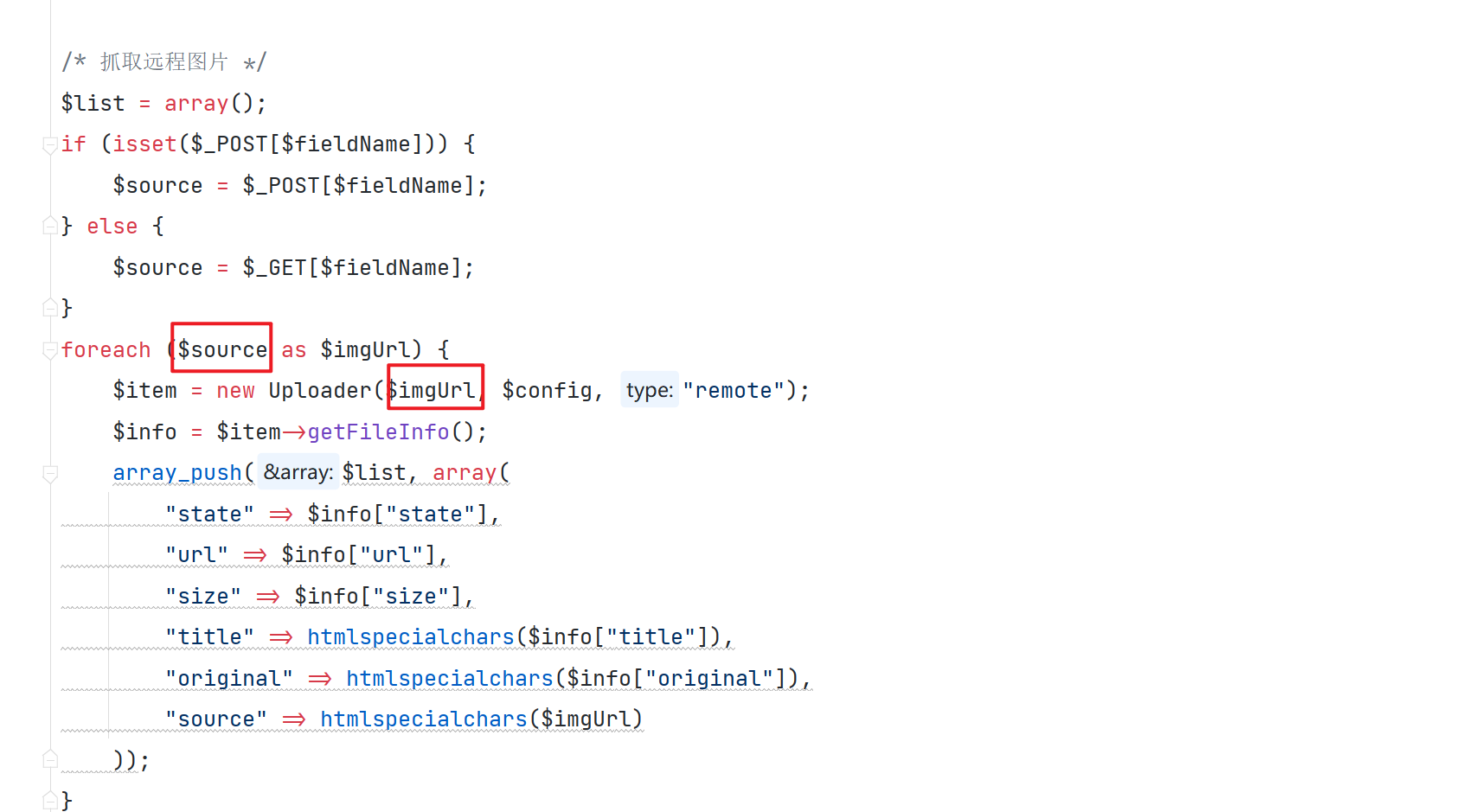
木鱼cms系统审计小结
MuYuCMS基于Thinkphp开发的一套轻量级开源内容管理系统,专注为公司企业、个人站长提供快速建站提供解决方案。 环境搭建 我们利用 phpstudy 来搭建环境,选择 Apache2.4.39 MySQL5.7.26 php5.6.9 ,同时利用 PhpStorm 来实现对项目的调试 …...

软件测试面试-一线大厂必问的测试思维面试题
五、测试思维5.1 打电话功能怎么去测?我们会从几个方面去测试:界面、功能、兼容性、易用性、安全、性能、异常。1)界面我们会测试下是否跟界面原型图一致,考虑浏览器不同显示比例,屏幕分辨率。2)功能&#…...
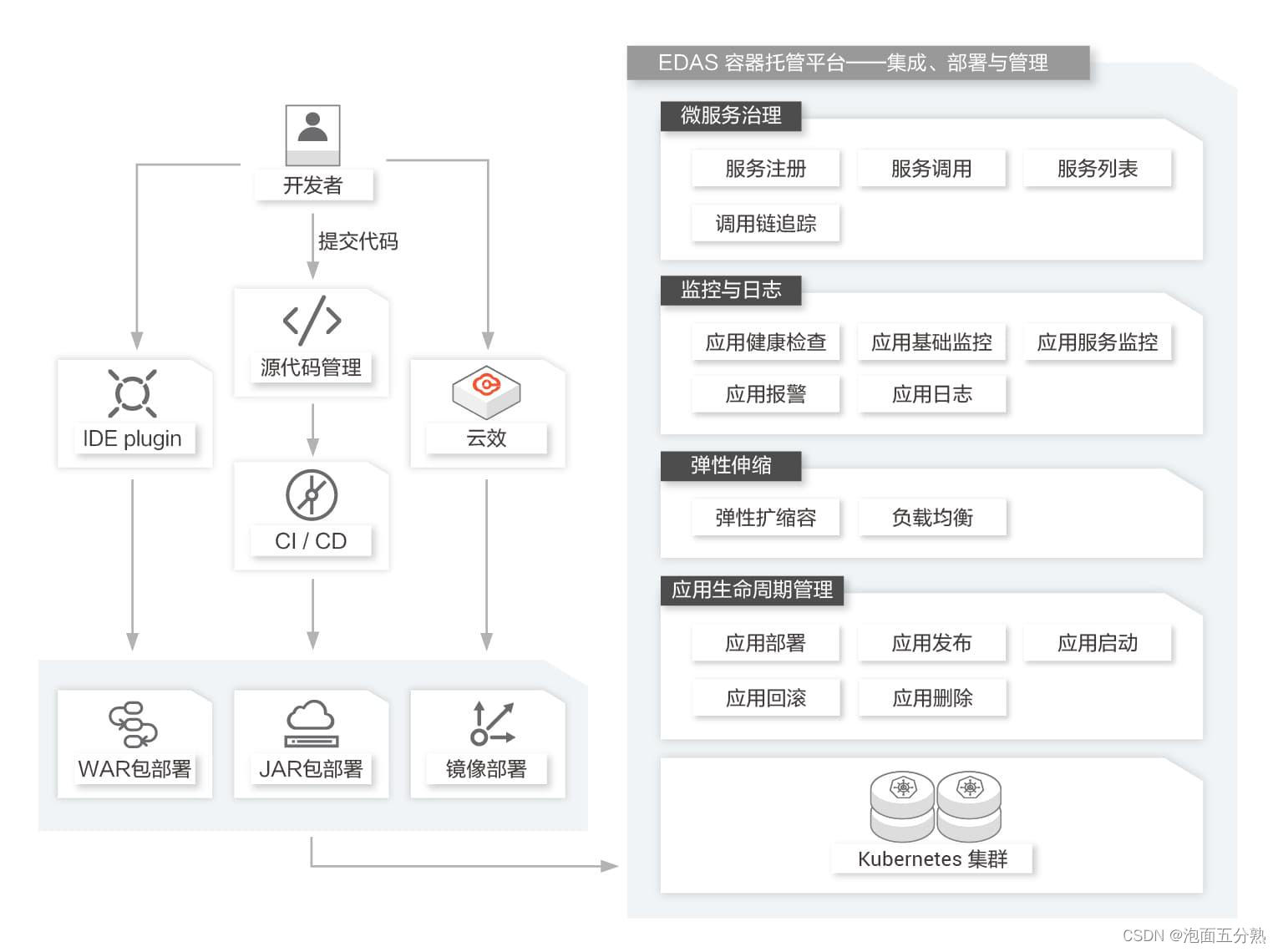
企业级分布式应用服务 EDAS
什么是企业级分布式应用服务EDAS企业级分布式应用服务EDAS(Enterprise Distributed Application Service)是一个应用托管和微服务管理的云原生PaaS平台,提供应用开发、部署、监控、运维等全栈式解决方案,同时支持Spring Cloud和Ap…...
弄懂 Websocket 你得知道的这 3 点
1. WebSocket原理 WebSocket同HTTP一样也是应用层的协议,但是它是一种双向通信协议,是建立在TCP之上的。 WebSocket是一种在单个TCP连接上进行全双工通信的协议。WebSocket API也被W3C定为标准。 WebSocket使得客户端和服务器之间的数据交换变得更加简…...

Appium构架及工作原理
一、appium结构简单来说appium充当一个中间服务器的功能,接收来自我们代码的请求,然后发送到手机上进行执行。二、初步认识appium工作过程1.appium是c/s模式的2.appium是基于webdriver协议添加对移动设备自动化api扩展而成的,所以具有和webdr…...

软件架构中“弹性”的多种含义
在软件架构领域的中文文档、书籍中,经常可以看到“弹性”这个专业术语,但在不同的语境下含义可能会不同。 在英语中,elastic 和 resilient 两个单词都可以翻译为“弹性的”,但是它们在软件架构中代表的含义却完全不同,…...

JAVA练习57- 罗马数字转整数、位1的个数
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目1-罗马数字转整数 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 二、题目2-位1的个数 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 …...
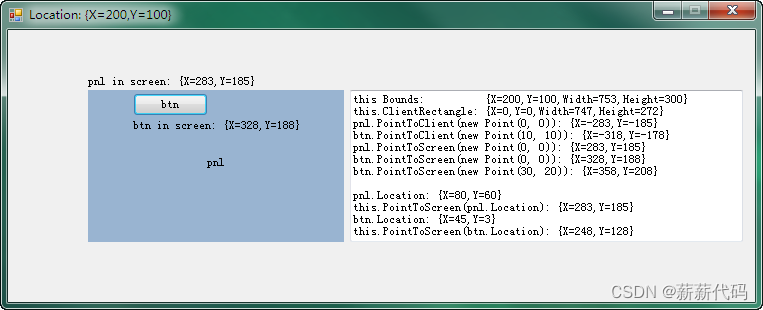
C#把图片放到picturebox上的指定位置,PointToClient与PointToScreen解读
1、C#中如何把图片放到picturebox上的指定位置 构造一个跟picturebox1一样大小的Bitmap, 设置给picturebox1, 然后在上面画图 Bitmap image new Bitmap(picturebox1.Size.Width, picturebox1.Size.Height); Graphics device Graphics.FromImage(imag…...
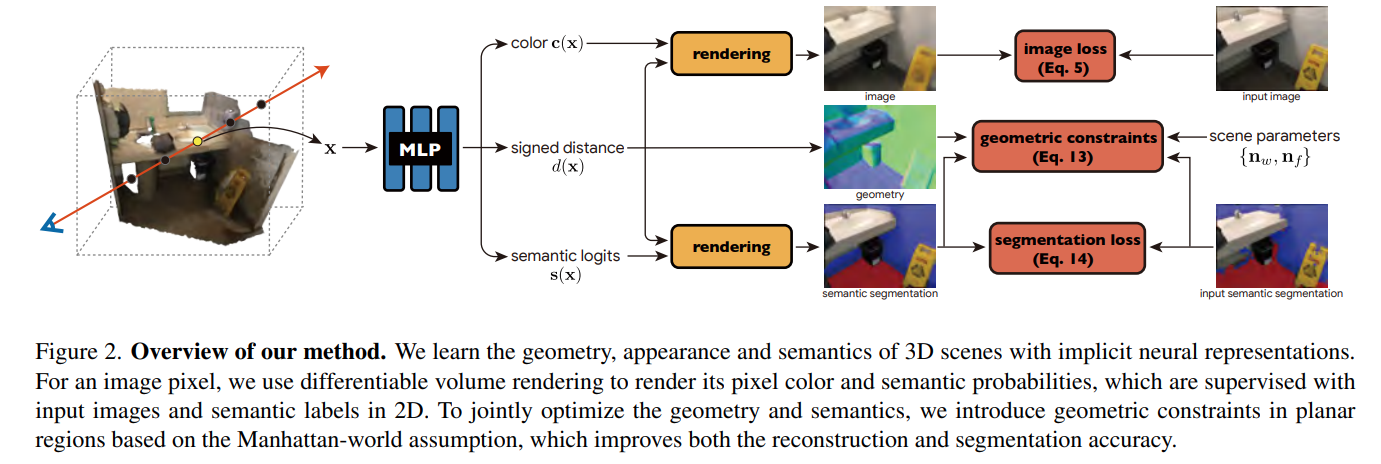
【论文笔记】Manhattan-SDF==ZJU==CVPR‘2022 Oral
Neural 3D Scene Reconstruction with the Manhattan-world Assumption 本文工作:基于曼哈顿世界假设,重建室内场景三维模型。 1.1 曼哈顿世界假设 参考阅读文献:Structure-SLAM: Low-Drift Monocular SLAM in Indoor EnvironmentsIEEE IR…...

环翠区中小学生编程挑战赛题解中学组T4:免费超市
题目描述 OITV电视台最近开设了名为“免费超市”的真人电视节目,在节目中,抽奖选拔的民间志愿者们将随机匹配进行两两对抗赛。每场比赛上,节目组设置 n n n件商品排成一排供选手挑选,两名选手将交替出手选中并拿走商品,每件商品有着不同的价值 a i a_i a...
的学习笔记)
关于Oracle树形查询(connect by)的学习笔记
1.查找员工 FORD的上级 Note:在查找时,应当注意树形是倒过来的。(自下而上),故此父亲节点是MGR ,而儿子节点是EMPNO –PRIOR MGREMPNO也是可以的。 以下两种方式均可以实现查找FORD的上级。 SQL> SQ…...

观看课程领奖品!Imagination中国区技术总监全面解读 IMG DXT GPU
此前,我们发布了一系列关于 IMG DXT GPU 的介绍,为了让更多读者了解其背后的技术及应用方向,我们特别邀请 Imagination 中国区技术总监艾克录制全新在线课程,为大家全面解读IMG DXT GPU。 点击这里,马上注册观看&…...

To_Heart—题解——[SCOI2012]奇怪的游戏
题意 link. 给定一个 nmn\times mnm 的棋盘,每次操作可以选择两个相邻的格子,让这两个各自上的数都 1。问最少多少次操作使得所有格子的数相等。如果永远不行则输出-1。 题解 因为相邻两个格子进行操作,而且是方格,所以很容易…...

Spring Boot Hello World 基于 IDEA 案例详解
一、Spring Boot 是什么 世界上最好的文档来源自官方的《Spring Boot Reference Guide》,是这样介绍的: Spring Boot makes it easy to create stand-alone, production-grade Spring based Applications that you can “just run”...Most Spring Boot…...
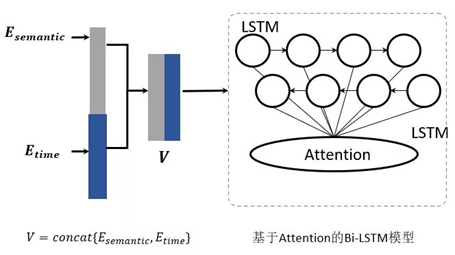
基于机器学习的异常检测与分析技术
传统的运维方式在监控、问题发现、告警以及故障处理等各个环节均存在明显不足,需要大量依赖人的经验,在数据采集、异常诊断分析、故障处理的效率等方面有待提高。 本关键技术面对传统运维故障处理效率低、问题定位不准确、人力成本高三大痛点࿰…...

pytest进阶之html测试报告
pytest进阶之html测试报告 目录:导读 前言 pytest-html生成报告 安装 生成报告 效果 错误用例截图 添加描述 小结 allure2生成报告 安装allure 安装pytest-allure-adaptor插件 生成xml格式报告 添加环境变量 运行allure生成报告 效果 总结 前言 …...

劳特巴赫仿真测试工具Trace32的基本使用(cmm文件)
劳特巴赫 Trace32 调试使用教程 使用PRACTICE 脚本(.cmm) 在TRACE32 中使用PRACTICE 脚本(*.cmm)将帮助你: 在调试器启动时立即执行命令根据您的项目需求自定义TRACE32PowerView用户界面加载应用程序或符号使调试操作具有可重复性, 并可用于验证目的和回归测试 自动启动脚本…...
盘点四种自动化测试模型实例及优缺点
一,线性测试 1.概念: 通过录制或编写对应应用程序的操作步骤产生的线性脚本。单纯的来模拟用户完整的操作场景。 (操作,重复操作,数据)都混合在一起。 2.优点: 每个脚本相对独立࿰…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
