算法:轮转数组---循环取模运算
1、题目:
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
2、分析特点:
-
轮转 ==> 取模运算 -
我们可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度,我们遍历原数组,将原数组下标为 i 的元素放至新数组下标为 (i+k) mod n 的位置,最后将新数组拷贝至原数组即可。
3、代码:
public void rotate(int[] nums, int k) {int n = nums.length;int[] newArr = new int[n];for (int i = 0; i < n; ++i) {newArr[(i + k) % n] = nums[i];}System.arraycopy(newArr, 0, nums, 0, n);}
4、复杂度分析:
- 时间复杂度: O(n),其中 n 为数组的长度。
- 空间复杂度: O(n)。
5、总结:
轮转、循环 k 步,要想到取模运算,另外需要一个新数组作为结果数组是因为如果我们不使用额外数组,我们直接将每个数字放至它最后的位置,这样被放置位置的元素会被覆盖从而丢失,所以需要一个新数组作为结果数组,最后拷贝回去原数组。
如果本文对你有帮助的话记得给一乐点个赞哦,感谢!
相关文章:

算法:轮转数组---循环取模运算
1、题目: 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 2、分析特点: 轮转 > 取模运算 我们可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度,我们遍历原数组&a…...
Vue教程
官网vue快速上手 vue示例图 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 代码:LearnVue...
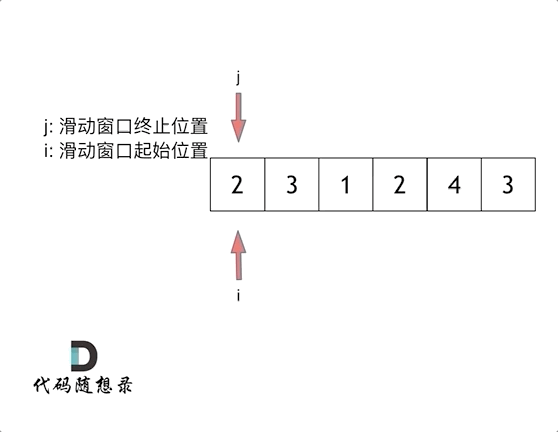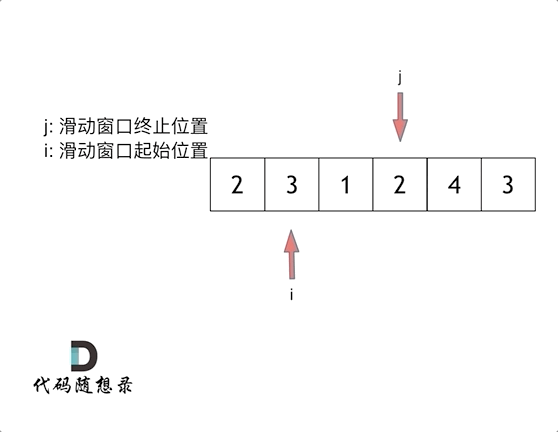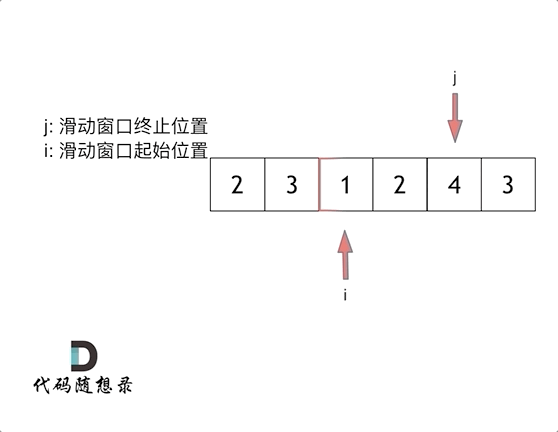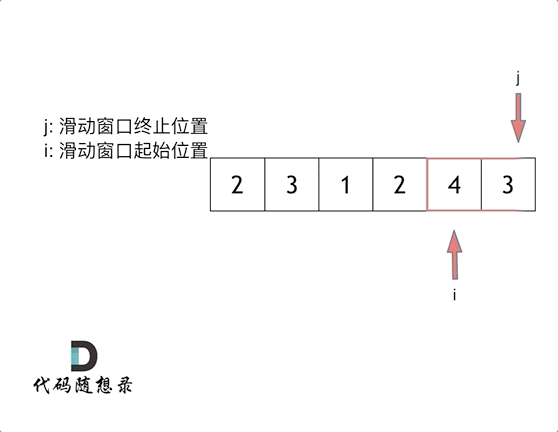
算法之双指针题型:
双指针例题小总结: 力扣27: 移除元素 力扣题目链接 双指针分为: 快慢双指针:同一个起点,同向出发 相向双指针:从两端出发,方向相反,终会相遇 经典的双指针(快慢双指…...

vue传递给后端时间格式问题
前端处理 首先前端使用moment.js进行处理 data.userEnrolDate moment(data.userEnrolDate).format(YYYY-MM-DD HH:mm:ss);后端处理 JsonFormat(timezone "GMT8", pattern "yyyy-MM-dd HH:mm:ss") DateTimeFormat(pattern "yyyy-MM-dd HH:mm:ss…...
php使用jwt作登录验证
1 在项目根目录下,安装jwt composer require firebase/php-jwt 2 在登录控制器中加入生成token的代码 use Firebase\JWT\JWT; use Firebase\JWT\Key; class Login extends Cross {/*** 显示资源列表** return \think\Response*/public function index(Request $r…...

【zlm】 PTS DTS
在音视频编码和传输中,PTS(Presentation Time Stamp)和DTS(Decoding Time Stamp)是两个关键的时间戳,用于确保音视频帧的顺序和同步。它们在多媒体处理中扮演重要的角色: PTS(Presen…...

【两周学会FPGA】从0到1学习紫光同创FPGA开发|盘古PGL22G开发板学习之DDR3 IP简单读写测试(六)
本原创教程由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处 适用于板卡型号: 紫光同创PGL22G开发平台(盘古22K) 一:盘古22K开发板(紫光同创PGL22G开发…...

第6章 内核模块符号导出实验(iTOP-RK3568开发板驱动开发指南 )
在上一小节中,给大家讲解了驱动模块传参实验,使用insmod命令加载驱动时可以进行参数的传递,但是每一个内核模块之间是相互独立的,那模块间的符号传递要怎样进行呢,让我们带着疑问来进行本章节的学习吧! 6.…...
第二种方法)
Android12.0首次开机默认授予app运行时权限(去掉运行时授权弹窗)第二种方法
1.概述 在12.0的系统产品开发中,在6.0以后对于权限的申请,都需要动态申请,所以会在系统首次启动后,在app的首次运行时,会弹出授权窗口,会让用户手动授予app运行时权限,在由于系统产品开发需要要求默认授予app运行时权限,不需要用户默认授予运行时弹窗,所以需要在首次开…...

conda和Python的虚拟环境如何结合使用,以及二者之间到底有什么区别?
问题描述 今天在复现streamlit的代码时(参考Streamlit 讲解专栏(一):安装以及初步应用),根据这篇博文指导,要先用以下指令创建一个虚拟环境: # 创建虚拟环境(使用venv&a…...

宇凡微YE09合封芯片,集成高性能32位mcu和2.4G芯片
合封芯片是指将主控芯片和外部器件合并封装的芯片,能大幅降低开发成本、采购成本、减少pcb面积等等。宇凡微YE09合封芯片,将技术领域推向新的高度。这款高度创新性的芯片融合了32位MCU和2.4G芯片,为各种应用场景提供卓越的功能和性能。 32位M…...

使用perf_analyzer和model-analyzer测试tritonserver的模型性能超详细完整版
导读 当我们在使用tritonserver部署模型之后,通常需要测试一下模型的服务QPS的能力,也就是1s我们的模型能处理多少的请求,也被称为吞吐量。 测试tritonserver模型服务的QPS通常有两种方法,一种是使用perf_analyzer 来测试&#…...
docker 部署springboot(成功、截图)
1.新建sringboot工程并打包 2.编写Dockerfile文件 # 基础镜像使用java FROM openjdk:8 # 作者 MAINTAINER feng # VOLUME 指定了临时文件目录为/tmp。 # 其效果是在主机 /var/lib/docker 目录下创建了一个临时文件,并链接到容器的/tmp VOLUME /tmp # 将jar包添加…...
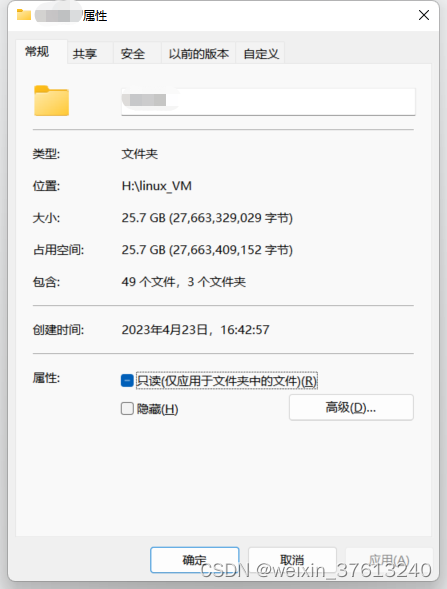
VMware ubuntu空间越用越大
前言 用Ubuntu 1604编译了RK3399的SDK,之后删了一些多余的文件,df - h 已用21G,但window硬盘上还总用了185GB,采用了碎片整理,压缩无法解决 1 启动Ubuntu后, 安装 VMware Tools(T) 、 2 打开ubuntu终端,压…...
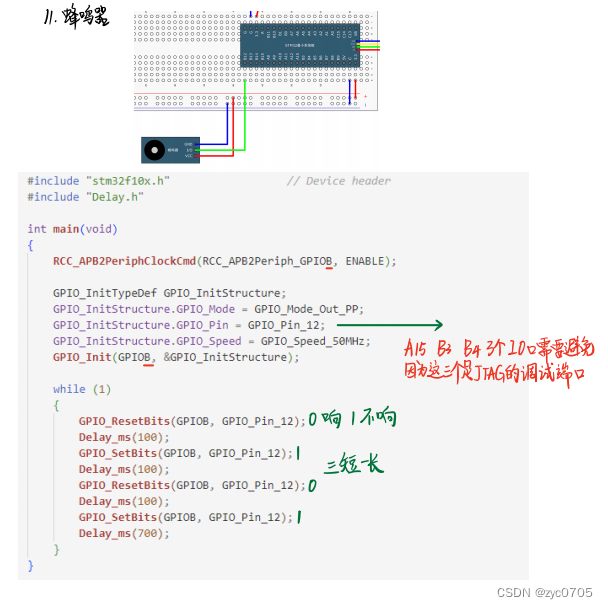
stm32 学习笔记:GPIO输出
一、GPIO简介 引脚电平 0-3.3V,部分可容忍5V,对输出而言最大只能输出3.3V, 只要可以用高低电平来控制的地方,都可以用GPIO来完成,如果控制的功率比较大的设备,只需加入驱动电路即可 GPIO 通用输入输出口,可配置为 8种 …...

css换行
强制显示一行,超出... .box{white-space: nowrap; /* 强制显示一行 */overflow: hidden;text-overflow: ellipsis; /* 超出... */ } 自动换行 一般默认制动换行 .box1{word-wrap:break-word; } 显示2行,超出... .box2 {overflow: hidden;display: -…...
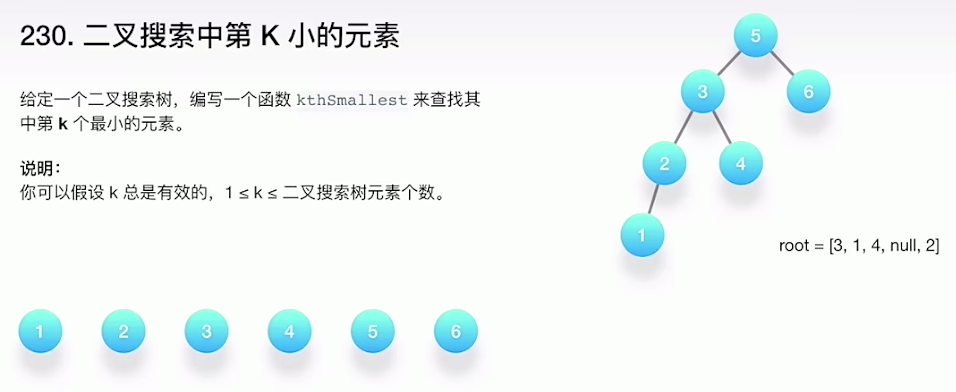
面试算法-常用数据结构
文章目录 数据结构数组链表 栈队列双端队列树 1)算法和数据结构 2)判断候选人的标准 算法能力能够准确辨别一个程序员的功底是否扎实 数据结构 数组 链表 优点: 1)O(1)时间删除或者添加 灵活分配内存空间 缺点: 2&…...
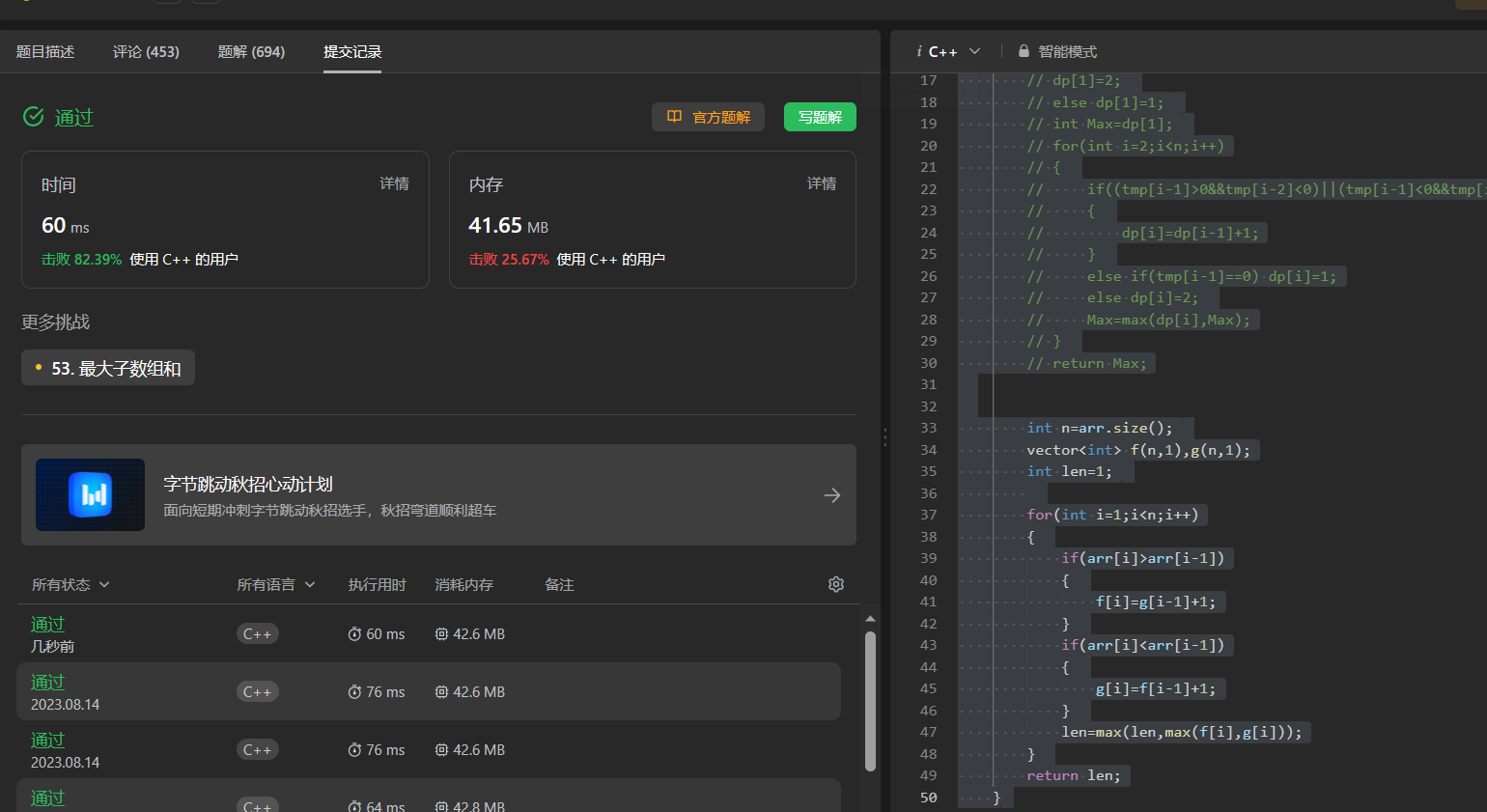
【动态规划刷题 10】等差数列划分 最长湍流子数组
413. 等差数列划分 链接: 413. 等差数列划分 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 nums ,返回…...

redis 配置与优化
目录 一、关系数据库和非关系型数据库 二、关系型数据库和非关系型数据库区别 三、非关系型数据库产生背景 四、redis 1、概念 2、redis的优点 3、redis为什么这么快 五、redis安装与配置 一、关系数据库和非关系型数据库 关系型数据库:关系型数据库是一个结…...

数据结构例题代码及其讲解-递归与树
树 树的很多题目中都包含递归的思想 递归 递归包括递归边界以及递归式 即:往下递,往上归 递归写法的特点:写起来代码较短,但是时间复杂度较高 01 利用递归求解 n 的阶乘。 int Func(int n) {if (n 0) {return 1;}else …...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
