《机器人学一(Robotics(1))》_台大林沛群 第 6 周 【轨迹规划_直线转折处抛物线平滑】Quiz 6
步骤:
1、 编程 将PPT 的例子 跑一遍, 确保代码无误
2、根据题目 修改 相关参数
文章目录
- 求解代码_Python
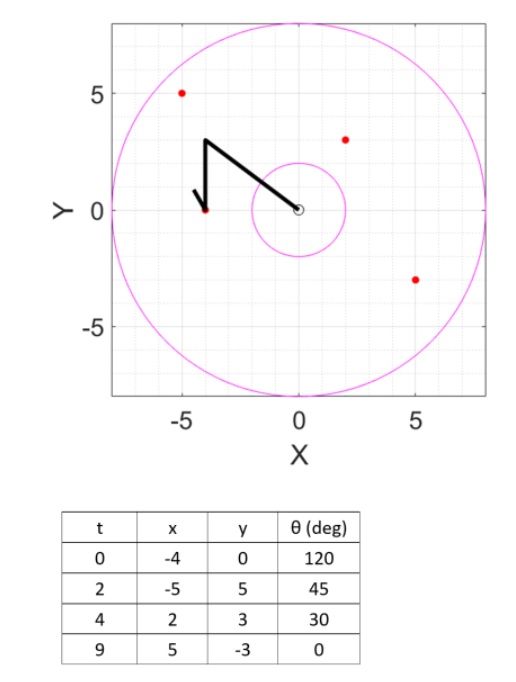
解决的问题: 线段间转折点 的 速度 不连续
解决方法: 将直线段 两端 修正为 二次方程式

二次项圆滑

求解代码_Python
import numpy as np
np.set_printoptions(precision=2,suppress = True) t0, t1, t2, tf = 0, 2, 4, 9
x0, x1, x2, xf = -4, -5, 2, 5
y0, y1, y2, yf = 0, 5, 3, -3
θ0, θ1, θ2, θf = 120, 45, 30, 0
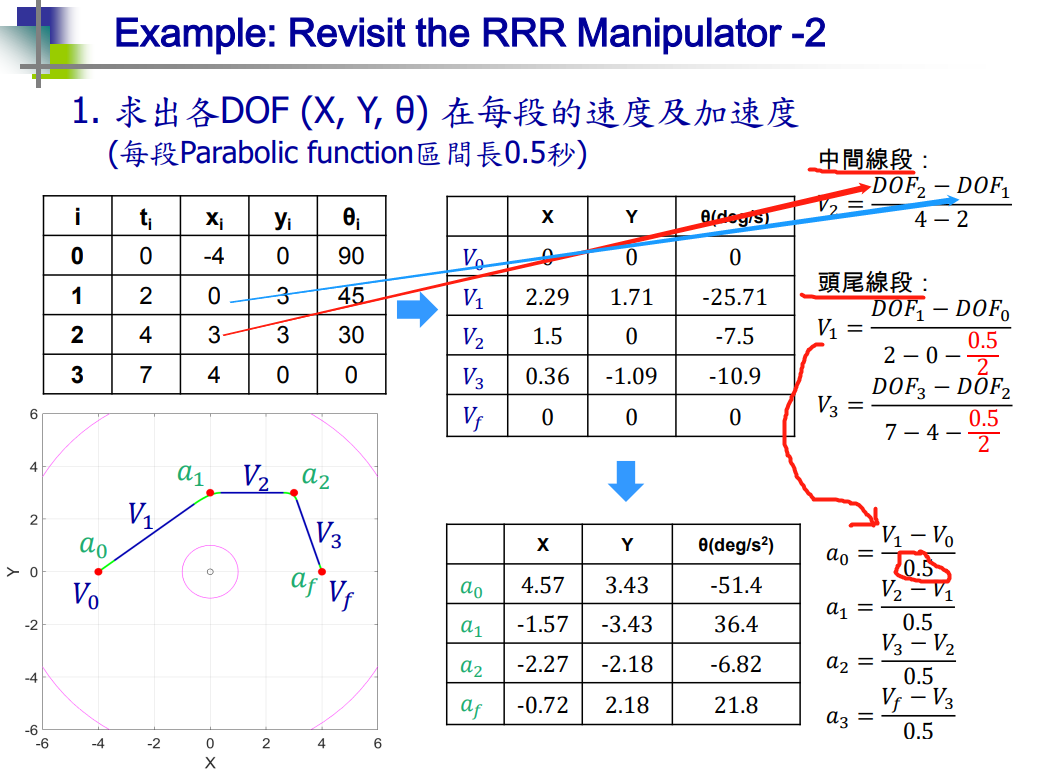
tk = 0.5### 1、求 各 DOF(X, Y, θ) 在每段的速度 及 加速度## 中间 线段 计算
def getV_in(x1, x2, t1, t2):return (x2 - x1)/(t2 - t1)## 头尾 线段 计算
def getV_0f(x1, x2, t1, t2):return (x2 - x1)/(t2 - t1 - tk/2)### 2、 建立 各 DOF(X, Y, θ) 在每段的方程
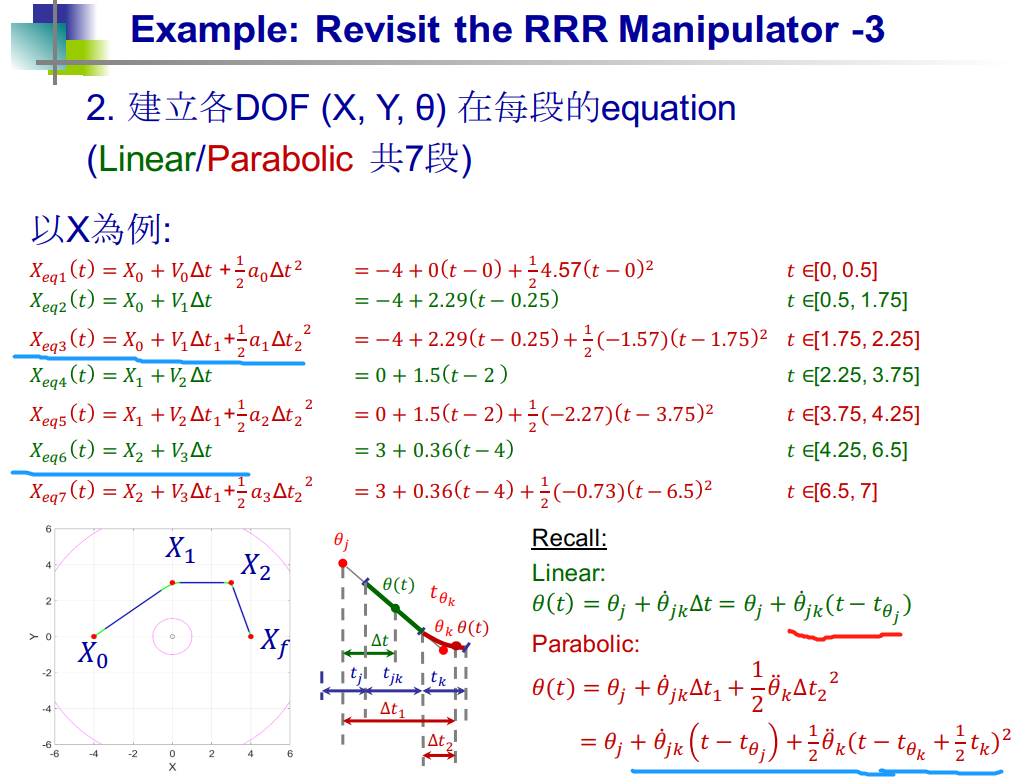
"""
平滑 t ∈ [0, 0.5]
直线 t ∈ [0.5, 1.75]
平滑 t ∈ [1.75, 2.25]
直线 t ∈ [2.25, 3.75]
平滑 t ∈ [3.75, 4.25]
直线 t ∈ [4,25, 8.5]
平滑 t ∈ [8.5, 9]
"""
## 求解 X(t)
## 平滑化 段
def getX_parabolic(x, V, a, ti0, ti1, t):return x + V * (t - ti0) + 0.5 * a * (t - ti1)**2## 直线段
def getX_linear(x, V, ti, t):return x + V * (t - ti)############# 求解 X 部分
print('X:')
V0 = 0
V1 = getV_0f(x0, x1, t0, t1)
V2 = getV_in(x1, x2, t1, t2)
V3 = getV_0f(x2, xf, t2, tf)
Vf = 0
print('V1[0.5 ~ 1.75]:', np.round(V1, 2))
print('V2[2.25 ~ 3.75]:', np.round(V2, 2))
print('V3[4.25 ~ 8.25]:', np.round(V3, 2)) def geta(V1, V2):return (V2 - V1)/tka0 = geta(V0, V1)
a1 = geta(V1, V2)
a2 = geta(V2, V3)
af = geta(V3, Vf)
print('a0:', np.round(a0, 2))
print('a1:', np.round(a1, 2))
print('a2:', np.round(a2, 2))
print('af:', np.round(af, 2))print('t ∈ [3.75, 4.25] t = 4 , X5 = :', np.round(getX_parabolic(x1, V2, a2, 2, 3.75, 4), 2))############# 求解 Y 部分
print('Y:')
V0 = 0
V1 = getV_0f(y0, y1, t0, t1)
V2 = getV_in(y1, y2, t1, t2)
V3 = getV_0f(y2, yf, t2, tf)
Vf = 0
print('V1:', np.round(V1, 2))
print('V2:', np.round(V2, 2))
print('V3:', np.round(V3, 2)) def geta(V1, V2):return (V2 - V1)/tka0 = geta(V0, V1)
a1 = geta(V1, V2)
a2 = geta(V2, V3)
af = geta(V3, Vf)
print('a0:', np.round(a0, 2))
print('a1:', np.round(a1, 2))
print('a2:', np.round(a2, 2))
print('af:', np.round(af, 2))print('t ∈ [3.75, 4.25] t = 4 , Y5 = :', np.round(getX_parabolic(y1, V2, a2, 2, 3.75, 4), 2))############# 求解 θ 部分
print('θ:')
V0 = 0
V1 = getV_0f(θ0, θ1, t0, t1)
V2 = getV_in(θ1, θ2, t1, t2)
V3 = getV_0f(θ2, θf, t2, tf)
Vf = 0
print('V1:', np.round(V1, 2))
print('V2:', np.round(V2, 2))
print('V3:', np.round(V3, 2)) def geta(V1, V2):return (V2 - V1)/tka0 = geta(V0, V1)
a1 = geta(V1, V2)
a2 = geta(V2, V3)
af = geta(V3, Vf)
print('a0:', np.round(a0, 2))
print('a1:', np.round(a1, 2))
print('a2:', np.round(a2, 2))
print('af:', np.round(af, 2))print('t ∈ [3.75, 4.25] t = 4 , θ5 = :', np.round(getX_parabolic(θ1, V2, a2, 2, 3.75, 4), 2))

第1题答案: -0.57//2.86//-42.86

第2题答案: 3.5//-1//-7.5

第3题答案: 0.63//-1.26//-6.32

第4题答案: -1.14//5.71//-85.71

第5题答案: 8.14//-7.71//70.71

第6题答案: -5.74//-0.53//2.37

第7题答案: -1.26//2.53//12.63

第8题答案: 1.82//2.98//30.07
相关文章:

《机器人学一(Robotics(1))》_台大林沛群 第 6 周 【轨迹规划_直线转折处抛物线平滑】Quiz 6
步骤: 1、 编程 将PPT 的例子 跑一遍, 确保代码无误 2、根据题目 修改 相关参数 文章目录 求解代码_Python 解决的问题: 线段间转折点 的 速度 不连续 解决方法: 将直线段 两端 修正为 二次方程式 二次项圆滑 求解代码_Python …...
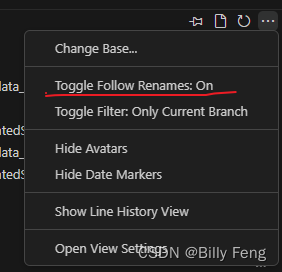
关于vscode的GitLens插件里的FILE HISTORY理解
最近在用vscode的GitLens插件开发项目遇到这个疑问,先看图: 每当我点击FILE HISTORY 一个commit时,正常来说显示器会自动将点击的提交版本和它上一个提交版本进行比较,如果单纯这么理解的话就错了,因为GitLens的File …...
通过idea实现springboot集成mybatys
概述 使用springboot 集成 mybatys后,通过http请求接口,使得通过http请求可以直接直接操作数据库; 完成后端功能框架;前端是准备上小程序,调用https的请求接口用。简单实现后端框架; 详细 springboot 集…...
算法_C++——移位字符串分组)
力扣(LeetCode)算法_C++——移位字符串分组
给定一个字符串,对该字符串可以进行 “移位” 的操作,也就是将字符串中每个字母都变为其在字母表中后续的字母,比如:“abc” -> “bcd”。这样,我们可以持续进行 “移位” 操作,从而生成如下移位序列&am…...

Vue2 与Vue3的区别?面试题
Vue 2和Vue 3是Vue.js框架的不同版本,在面试中经常涉及到它们之间的区别。以下是Vue 2和Vue 3的主要区别: 性能提升:Vue 3在性能方面进行了优化。Vue 3引入了更高效的Diff算法,提高了渲染性能。此外,Vue 3还进行了代码…...

java代码:Random和Scanner应用的小例子-猜数字小游戏
//java代码:Random和Scanner应用的小例子-猜数字小游戏 package com.test; import java.util.Random; import java.util.Scanner; /* * 需求:猜数字小游戏。 * 系统产生一个1-100之间的随机数,请猜出这个数据是多少? * * 分析…...
python调用git出错:ImportError: Failed to initialize: Bad git executable.
报错信息 #报错信息 Traceback (most recent call last): File “”, line 1, in File “C:\Python27\lib\site-packages\git_init_.py”, line 85, in raise ImportError(‘Failed to initialize: {0}’.format(exc)) ImportError: Failed to initialize: Bad git executab…...

【C语言】入门——指针
目录 编辑 1.指针是什么 2.指针类型和指针运算 2.1指针-整数 2.2指针-指针 2.3指针的关系运算 3.野指针 3.1野指针成因 👍指针未初始化: 👍指针越界访问: 👍指针指向空间释放: 3.2如何规避野指针 …...

C#_预处理指令
1. 预处理器指令指导编译器在实际编译开始之前对信息进行预处理。 所有的预处理器指令都是以 # 开始。且在一行上,只有空白字符可以出现在预处理器指令之前。预处理器指令不是语句,所以它们不以分号(;)结束。 C# 编译器没有一个单…...
)
容器命令(docker)
文章目录 前言一、docker容器命令0、准备工作1、新建容器并启动2、退出容器3、列出所有的运行的容器4、删除容器5、启动和停止容器的操作 总结 前言 本文主要介绍docker中与容器相关的一些命令,是对狂神课程的一些总结,作为一个手册帮助博主和使用docke…...

Vue3 ElementPlus el-cascader级联选择器动态加载数据
参考了这位的大佬的写法 element el-cascader动态加载数据 (多级联动,落地实现)_el-cascader 动态加载_林邵晨的博客-CSDN博客 <el-cascader style"width: 300px" :props"address" v-model"addressValue" …...
(一、字符串相邻元素删除类型))
leetcode分类刷题:栈(Stack)(一、字符串相邻元素删除类型)
1、在leetcode分类刷题:基于数组的双指针(一、基于元素移除的O(1)类型)题目中,采用双指针之快慢指针的算法来解决。 2、字符串相邻元素的删除问题,用栈来进行管理,会非常有效;这种题型排在后面的…...
你还在找淘宝商品信息查询的接口吗?
你还在找淘宝商品信息查询的接口吗?,不用找了,我这有,免费测试 在很多行业,比如淘客、商品采集、刊登、数据分析行业都需要用到相关的商品接口,但是官方一般又没有开放这些接口,怎么办ÿ…...
dll修复精灵,dll修复工具下载方法分享,mfc140u.dll缺失损坏一键修复
今天,我将为大家分享一个关于mfc140u.dll的问题。首先,我想问一下在座的网友们,有多少人知道mfc140u.dll是什么?又有多少人知道它的作用以及如何解决这个问题呢?在接下来的演讲中,我将详细介绍mfc140u.dll的…...

[LINUX使用] iptables tcpdump
iptables: 收到来自 10.10.10.10 的数据后都丢弃 iptables -I INPUT -s 10.10.10.10 -j DROP 直接 reject 来自 10.10.10.* 网段的数据 iptables -I INPUT -s 10.10.10.0/24 -j REJECT tcpdump: dump eth0的数据到本地 tcpdump -i eth0 -w dump.pcap 只抓 目的地址是 10…...

百度文心一率先言向全社会开放 应用商店搜“文心一言”可直接下载
8月31日,文心一言率先向全社会全面开放。广大用户可以在应用商店下载“文心一言APP”或登陆“文心一言官网”(https://yiyan.baidu.com) 体验。同时,企业用户可以直接登录百度智能云千帆大模型平台官网,调用文心一言能…...

【100天精通Python】Day56:Python 数据分析_Pandas数据清洗和处理
目录 数据清洗和处理 1.处理缺失值 1.1 删除缺失值: 1.2 填充缺失值: 1.3 插值: 2 数据类型转换 2.1 数据类型转换 2.2 日期和时间的转换: 2.3 分类数据的转换: 2.4 自定义数据类型的转换: 3 数…...

【vue】使用无障碍工具条(详细)
引入:使用的是太阳湾的无障碍工具条,代码地址:https://gitee.com/tywAmblyopia/ToolsUI 具体步骤:下载代码后,将其中的 canyou 文件夹拖入 vue 项目中的 public 文件夹中; 上图是在项目目录中的样子&#…...

java实现命令模式
命令模式是一种行为设计模式,它允许您将请求封装为对象,以便您可以将其参数化、队列化、记录和撤销。在 Java 中实现命令模式涉及创建一个命令接口,具体命令类,以及一个接收者类,该接收者类执行实际操作。下面是一个简…...
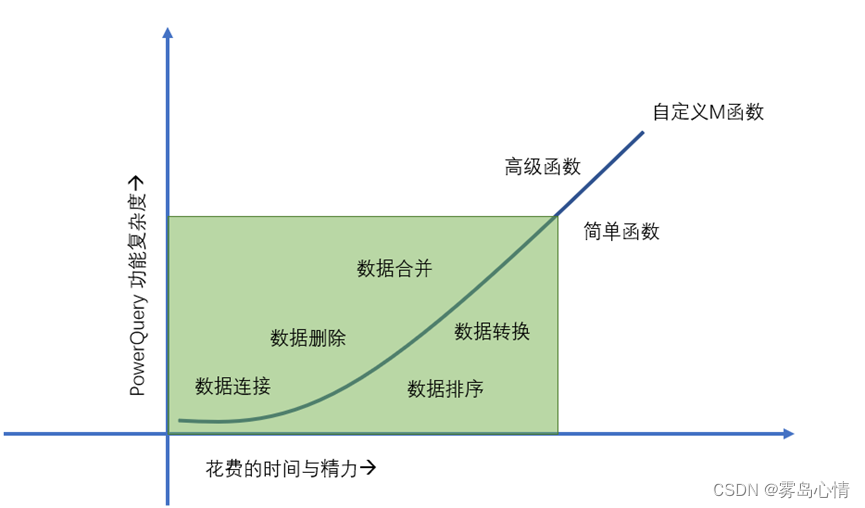
【PowerQuery】PowerQuery学习路径
PowerQuery这么好,怎么去学习呢?相信很多初读本书的朋友迫切的希望了解整个PowerQuery全景知识和它提供的相应的功能。但是对于PowerQuery来说,一开始就会进行自定义函数的构建当然也是不可能的,这里有相应的学习路径来进行由浅入深的学习,帮助读者更好的理解PowerQuery的…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
