精讲算法的时间复杂度
目录
一、算法效率
1.算法效率
1.1如何衡量一个算法的好坏
1.2算法的复杂度
二、时间复杂度
1.时间复杂度的概念
2.大O的渐进表示法
3.常见时间复杂度的计算举例
三、空间复杂度
一、算法效率
1.算法效率
1.1如何衡量一个算法的好坏
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
1.2算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
二、时间复杂度
1.时间复杂度的概念
时间复杂度的定义:时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
请计算下Func1中的++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}我们可以得出Func1执行的次数:F(N)=N^2+2*N+10
当N=10 F(N)=30;
当N=100 F(N)=10210;
当N=1000 F(N)=1002010;
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.大O的渐进表示法
大O符号:适用于描述函数渐进行为的数学符号。
推导大O的方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
有些大O的推导类似于高等数学中的取极限
就例如Func1
使用大O的渐进表示法以后,Func1的时间复杂度为O(N^2)
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
当N的取值非常大时我们可以省略数据中的一些数,取个大概,看着是不是类似于高等数学中的取极限
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般关注的是算法的最坏运行情况,随意数组中搜索数据的时间复杂度为O(N)。
3.常见时间复杂度的计算举例
实例1:
计算Func的时间复杂度?
void Func(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}Func执行次数表达式:F(N)=2*N+10
当N=10 F(N)=30
当N=1000 F(N)=2010
当N=1000000 F(N)=20000010
当n取很大的数值时表达式中的10可以省略,无论N乘不乘以2都是在一个数量级,也可以省略,这样我们就得到Func的之间复杂度为N,表示为O(1)。
实例2:
计算Func的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}Func的执行次数表达式为:F(N)=M+N
这里我们就要分情况讨论了
情形1:当M>>N时,根据高等数学求极限的思想N可以省略
所以, 我们可以得到Func的时间复杂度为M,表示为O(M)。
情形2:当M<<N是,同理可得Func的时间复杂度为N,表示为O(N)。‘
情形3:当M==N时,Func的执行次数表达式可以表示为F(N)=2M或者F(N)=2N
Func的时间表达式为O(N)或者O(M)。
实例3:
计算Func的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}Func的计算表达式为F(N)=100
根据大O的推导1,我们可以很轻松的得到Func的时间复杂度为O(1)。
实例4:
计算strchr的时间表达式?
const char * strchr ( const char * str, int character );库函数strchr表示在一个字符串中查找一个字符
这道题目我们也要分情况
最好基本操作执行一次,所以时间复杂度为O(1)
平均基本操作执行2/N次,所以时间复杂度为O(N/2)
最坏我们要遍历整个数组基本操作执行N次,所以时间复杂度为O(N)。
实例5:
计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}这是一个冒泡函数时间复杂度的计算,通过前面的几道时间复杂度的计算我们发现可以通过阅读代码计算出时间复杂度,乍一看这道题我们很难阅读代码获得答案。
这里也要分情况:
情形一:所给的一组数刚好是拍好顺序的,也就是最好的情况,也要进行n-1次比较,所以时间复杂度为O(N)。
情形二:所给的一组数是杂乱顺序的

我们不难发现执行次数是等差数列,根据等差数列的求和的到执行次数的表达式:F(N)=n*(n-1)/2
所以时间复杂度为O(N ^2)。
实例6:
计算BinarySearch(二分法)的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}假设我们有N个数,最好的情况为执行一次找到,最坏的情况为一直折半下去,直到剩下最后一个数字,也就是我们要找的那个数字,所以执行次数的表达式为2^x=N,解这个表达式x=logN,所以二分法的时间复杂度为O(logN)。
ps:logN在算法分析中表示的是底数为2,对数为N。
实例7:
计算阶乘递归的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}基本操作执行了N次,时间复杂度为O(N)。
总结:递归算法时间复杂度是多次调用的累加
实例8:
计算斐波那契递归的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
} 所以时间复杂度为O(2^N)。
所以时间复杂度为O(2^N)。
三、空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1:
计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
实例2:
计算斐波那契数列的空间复杂度?
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}实例3:
计算结阶乘递归的空间复杂度?
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}答案及分析:
1. 实例1使用了常数个额外空间,所以空间复杂度为 O(1)
2. 实例2动态开辟了N个空间,空间复杂度为 O(N)
3. 实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
相关文章:

精讲算法的时间复杂度
目录 一、算法效率 1.算法效率 1.1如何衡量一个算法的好坏 1.2算法的复杂度 二、时间复杂度 1.时间复杂度的概念 2.大O的渐进表示法 3.常见时间复杂度的计算举例 三、空间复杂度 一、算法效率 1.算法效率 1.1如何衡量一个算法的好坏 long long Fib(int N) {if(N <…...
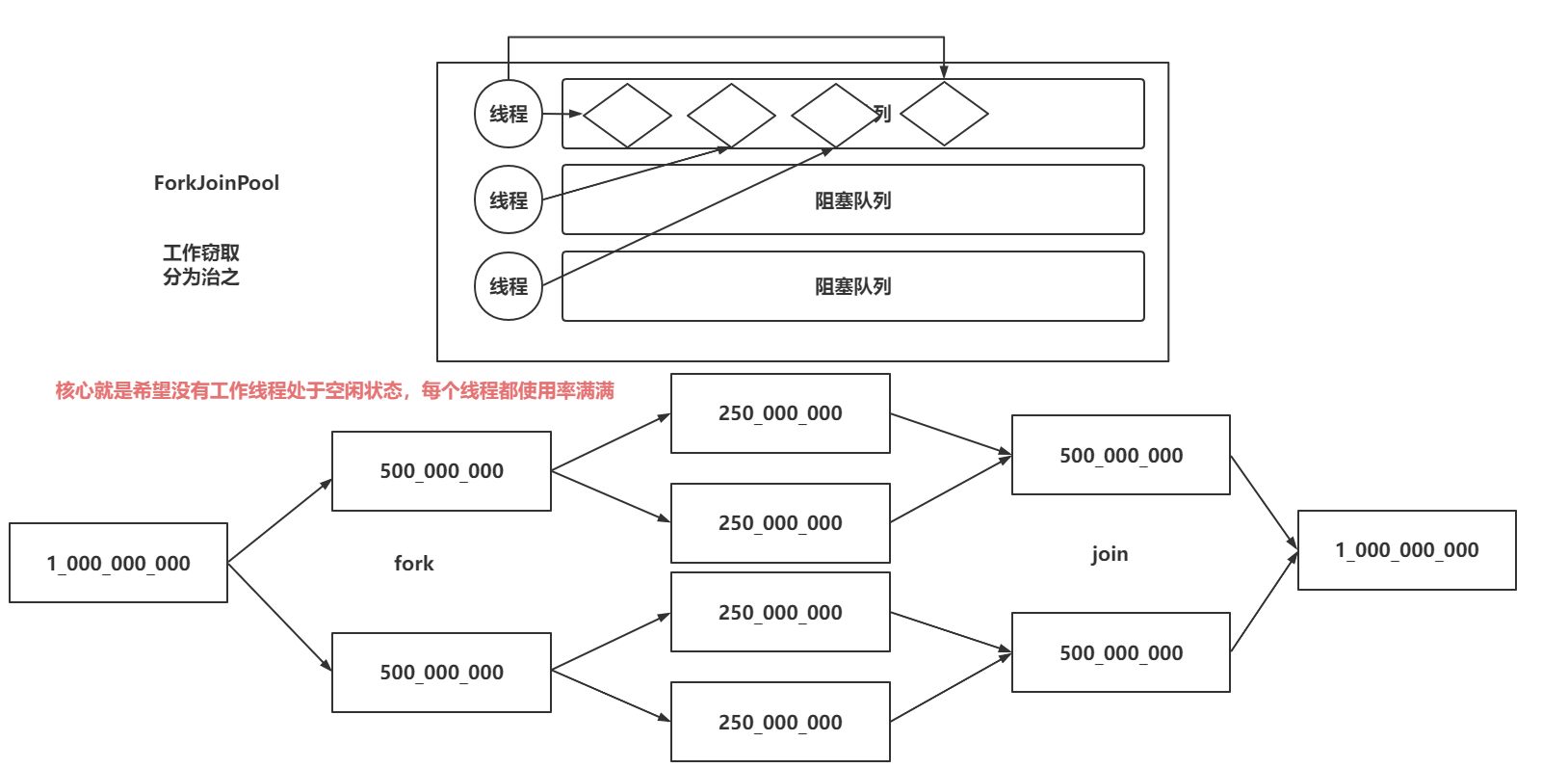
java八股文面试[多线程]——newWorkStealingPool
newWorkStealingPool是什么? newWorkStealingPool简单翻译是任务窃取线程池。 newWorkStealingPool 是Java8添加的线程池。和别的4种不同,它用的是ForkJoinPool。 使用ForkJoinPool的好处是,把1个任务拆分成多个“小任务”,把这…...

STM32--RTC实时时钟
文章目录 Unix时间戳时间戳转换BKPRTC简介RTC框图硬件电路RTC的注意事项RTC时钟实验工程 Unix时间戳 Unix 时间戳是从1970年1月1日(UTC/GMT的午夜)开始所经过的秒数,不考虑闰秒。 时间戳存储在一个秒计数器中,秒计数器为32位/64…...

【N2】例题学习笔记
N2例题 《新"日本语能力测试"例题集》 听力原稿(PDF) 【10】 【問い】この筆者から見た「仕事ができる人」の特徴はどんなことか。 【提问】这位作者认为,仕事能力强的人具有什么特点呢? 【11】 文章 下の文章は、企業のあり方について…...

【数据分享】2006-2021年我国城市级别的道路、桥梁、管线建设相关指标(10多项指标)
《中国城市建设统计年鉴》中细致地统计了我国城市市政公用设施建设与发展情况,在之前的文章中,我们分享过基于2006-2021年《中国城市建设统计年鉴》整理的2006—2021年我国城市级别的市政设施水平相关指标、2006-2021年我国城市级别的各类建设用地面积数…...

视觉SLAM14讲笔记-第7讲-视觉里程计2
直接法的引出 直接法是视觉里程计另一个主要分支,它与特征点法有很大的不同。 使用特征点法估计相机运动时,我们把特征点看作固定在三维空间的不动点。根据它们在相机中的投影位置,通过最小化重投影误差来优化相机运动。 相对地,…...

MySQL——单行函数和分组函数
2023.9.3 单行函数的SQL语句学习笔记如下: #常见单行函数介绍(部分省略) #字符函数 #将姓变大写,名变小写,然后拼接。 SELECT CONCAT(UPPER(last_name), ,LOWER(first_name)) AS 姓名 FROM employees; # 姓名中首字符…...

百度百科词条怎么更新?怎么能顺利更新百科词条?
企业和个人百度百科词条的更新对于他们来说都具有重要的意义,具体如下: 对企业来说: 塑造品牌形象:百度百科是一个常被用户信任并参考的知识平台,通过更新企业词条可以提供准确、全面的企业信息,帮助企业塑…...

PPT怎么转换为PDF格式,收藏这两个在线工具。
PPT是一种常用的演示文稿格式,它可以包含丰富的动画效果和超链接,让你的内容更加生动和有趣。但是,如果你想将PPT分享给别人,或者在不同的设备上查看,你可能会遇到一些问题,比如: PPT文件太大&a…...

八大排序算法----堆排序
堆排序的基本步骤:(以从大到小的顺序排序为例) 1.构建大顶堆(每个结点的值都大于或等于其左右孩子结点的值) 2.排序:每次堆顶的元素取出来(整个堆中值最大),与最后一个…...
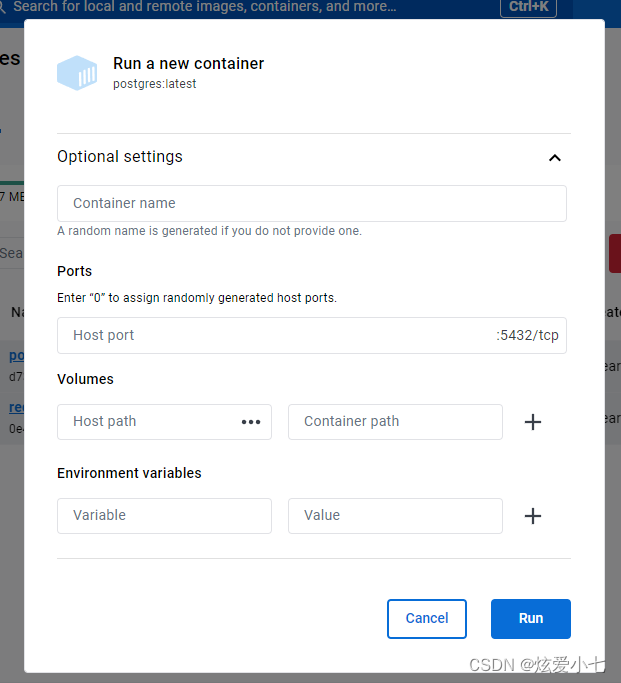
Docker Desktop 设置镜像环境变量
点击run 展开Optional settings container name :容器名称 Ports:根据你需要的端口进行输入,不输入则默认 后面这个 比如我这个 5432 Volumes:卷,也就是做持久化 需要docker 数据保存的地方 Environment variables…...
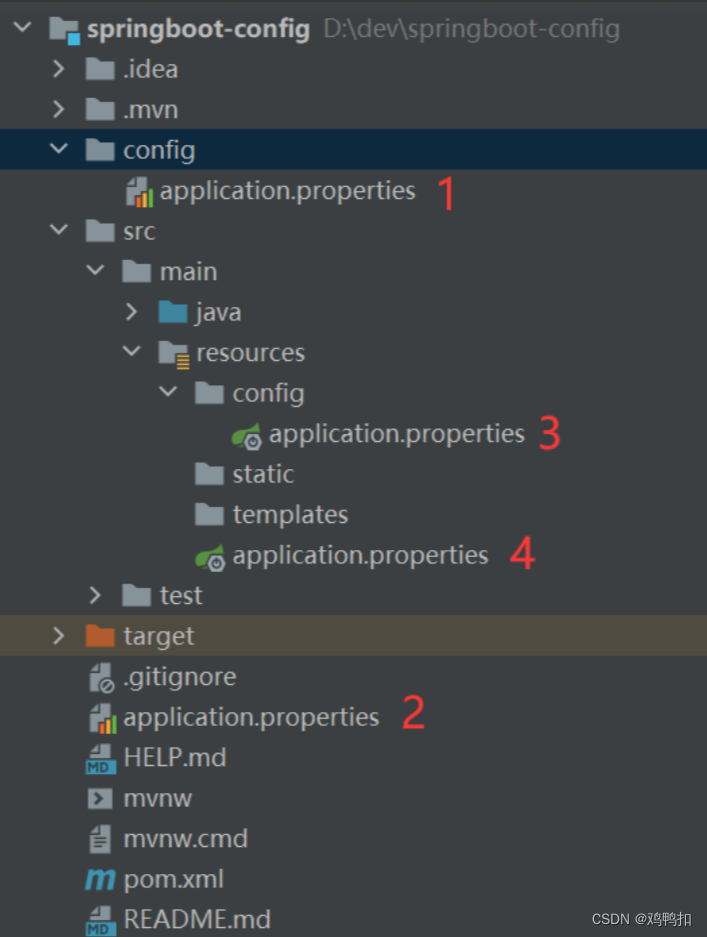
springboot之一:配置文件(内外部配置优先顺序+properties、xml、yaml基础语法+profile动态切换配置、激活方式)
配置的概念: Spring Boot是基于约定的,所以很多配置都有默认值,但如果想使用自己的配置替换默认配置的话,就可以使用application.properties或者application.yml(application.yaml)进行配置。 注意配置文件的命名必须是applicat…...

涛然自得周刊(第 5 期):蝲蛄吟唱的地方
作者:何一涛 日期:2023 年 8 月 20 日 涛然自得周刊主要精选作者阅读过的书影音内容,不定期发。历史周刊内容可以看这里。 电影 《沼泽深处的女孩》 改编自小说《蝲蛄吟唱的地方》,主角是一位在沼泽地独自生活并长大的女孩&…...

Android Ble蓝牙App(七)扫描过滤
Ble蓝牙App(七)扫描过滤 前言目录正文一、增加菜单二、使用MMKV① 添加依赖② 封装MMKV③ 使用MMKV 三、过滤空设备名四、过滤Mac地址五、过滤RSSI六、源码 前言 在上一篇文章中了解了MTU的相关知识以及对于设备操作信息的展示,本篇文章中将增…...

小程序当前页面栈以及跳转
1.调用页面栈刷新接口 let pages getCurrentPages(); //当前页面栈 if (pages.length > 1) { let beforePage pages[pages.length - 2]; //获取上一个页面实例对象 beforePage.$vm.getActivityLi…...
)
jQuery获取表单的值val()
(1)页面中有很多元素,包括表单中的输入项,如输入文本框等;获取、设置、输入文本框的值;val()方法。 (2)也包括<p>、<span>等元素;获取、设置这些元素的文本…...

【专栏必读】数字图像处理(MATLAB+Python)专栏目录导航及学习说明
文章目录 第一章:绪论第二章:数字图像处理基础第三章:图像基本运算第四章:图像的正交变换第五章:图像增强第六章:图像平滑第七章:图像锐化第八章:图像复原第九章:图像形态…...

2023年非证券类投资银行业发展报告
第一章 行业概况 非证券投资银行业是一个专门为公司、政府和高净值个人提供金融服务的行业,与传统的证券投资银行不同,其主要业务不涉及证券交易,而是注重为客户提供咨询服务、融资和投资管理等服务。 非证券投资银行通常涉及的业务领域包括…...
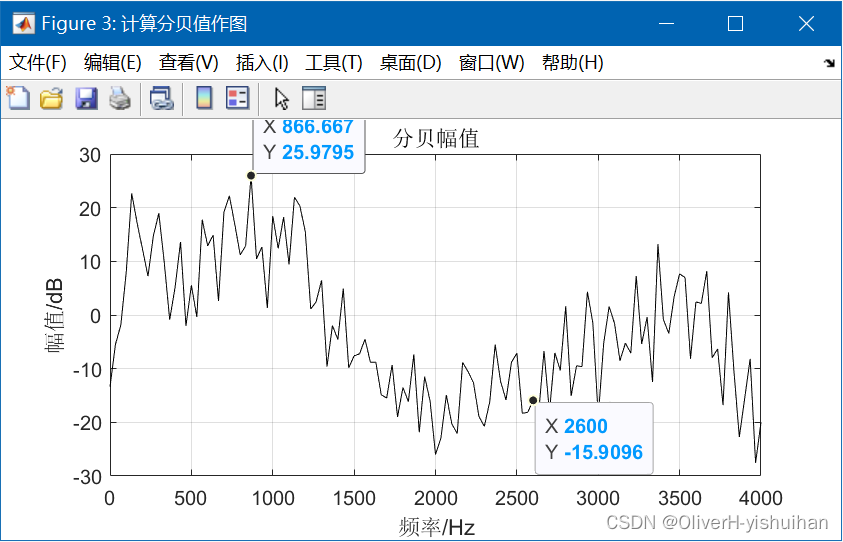
Matlab 如何把频谱图的纵坐标设置为分贝刻度
Matlab 如何把频谱图的纵坐标设置为分贝刻度 Matlab代码如下: % 如何把频谱图的纵坐标设置为分贝刻度 % % pr2_2_6 clc; clear; close all;load pr2_2_6_sndata1.mat % 读入数据 X fft(y); % FFT n2 1:L/21; % 计算正频率…...
)
VUE写后台管理(2)
VUE写后台管理(2) 1.环境2.Element界面3.Vue-Router路由后台1.左导航栏2.上面导航条 1.环境 1.下载管理node版本的工具nvm(Node Version Manager) 2.安装node(vue工程的环境管理工具):nvm install 16.13.0 3.安装vue工…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
