Erlang:Linux下使用observer、debugger进行调试
之前写了一篇文章Erlang:使用observer连接远程服务器进行调试,内容是绕过Linux服务器缺失’wxe_driver.so’的wxWidgets环境,启动observer远程连接实现observer调试。
本文则讨论在Linux环境下通过编译安装的方式,保证wxWidgets环境可用性,从而可以正常启动observer。
准备
系统:centos 7.9(可以是WSL子系统)
Erlang源码:Erlang/OTP 22.3.4.26
wxWidgets源码:wxWidgets-3.0.5
安装编译环境
yum update #更新系统
yum -y install make gcc gcc-c++ bzip2
安装wxWidgets
#安装wxWidgets依赖
yum -y install gtk2-devel binutils-devel
# 下载源码
wget https://github.com/wxWidgets/wxWidgets/releases/download/v3.0.5/wxWidgets-3.0.5.tar.bz2
# 解压
tar -xvf wxWidgets-3.0.5.tar.bz2
# 进入源码目录
cd wxWidgets-3.0.5
# 配置与编译(不要加--disable-shared,否则erlang configure的时候会wx:link program失败)
./configure --prefix=/usr/local/wxWidgets-3.0.5 --with-regex=builtin --with-gtk --enable-unicode --build=i686-pc-linux
make && make install
# 设置环境
cd /ets/ld.so.conf.d
echo "/usr/local/wxWidgets-3.0.5/lib" > wxWidgets.conf
ldconfig
vim /etc/profile.d/wxWidgets.sh
# 添加内容
export WXPATH=/usr/local/wxWidgets-3.0.5
export PATH=$WXPATH/bin:$PATH
# 添加结束
source /ets/profile
# 检查wx是否安装成功
wx-config --version
3.0.5 #输出
安装erlang
# 安装erlang相关依赖
yum install -y epel-release
yum install -y m4 openssl openssl-devel ncurses-devel unixODBC unixODBC-devel
# 下载源码
wget https://github.com/erlang/otp/releases/download/OTP-22.3.4.26/otp_src_22.3.4.26.tar.gz
# 进入源码目录
cd otp_src_22.3.4.26
# 配置与编译
./configure --prefix=/usr/local/erl_22.3.4.26 --enable-hipe --enable-threads --enable-smp-support --enable-kernel-pool --without-javac
make && make install
# 设置环境
vim /etc/profile.d/erl.sh
# 添加内容
export ERLPATH=/usr/local/erl_22.3.4.26
export PATH=$ERLPATH/bin:$PATH
# 添加结束
source /ets/profile
# 验证erlang是否安装成功
erl
至此erlang环境安装成功,observer、debugger也可以正常使用了。
相关文章:

Erlang:Linux下使用observer、debugger进行调试
之前写了一篇文章Erlang:使用observer连接远程服务器进行调试,内容是绕过Linux服务器缺失’wxe_driver.so’的wxWidgets环境,启动observer远程连接实现observer调试。 本文则讨论在Linux环境下通过编译安装的方式,保证wxWidgets环境可用性&am…...
2023 年高教社杯全国大学生数学建模竞赛-E 题 黄河水沙监测数据分析详解+思路+Python代码
2023 年高教社杯全国大学生数学建模竞赛-E 题 黄河水沙监测数据分析 十分激动啊啊啊题目终于出来了!!官网6点就进去了结果直接卡死现在才拿到题目,我是打算A-E题全部做一遍。简单介绍一下我自己:博主专注建模四年,参与…...

一生一芯10——verilator v5.008环境搭建
搜索 verilator 官网,得到网址如下: https://www.veripool.org/verilator/ 点击download 找到 git quick install 可以看到git快捷安装所需命令行 可以看到,需要预先安装下面的包文件,去掉前面的#注释符号进行安装 直接进行下面…...

信息化发展27
关键技术一云安全技术 云安全研究主要包含: 一是云计算技术本身的安全保护工作, 涉及相应的数据完整性及可用性、隐私保护性以及服务可用性等方面的内容; 二是借助于云服务的方式来保障客户端用户的安全防护需求, 通过云计算技术…...

leetcode做题笔记129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。…...

任务管理系统所需功能概述
"任务管理需要有哪些功能?清晰的任务创建与编辑、智能分类和标签系统、提醒与通知功能、进度跟踪与报告、协作与共享功能、集成与兼容性。" 一款优秀的任务管理工具可以帮助我们有效地规划、执行和监控各项任务,提高工作效率。本文将探讨一款理…...

一文学会K8s集群搭建
环境准备 节点数量:2台虚拟机 centos7硬件配置:master节点内存至少3G(2G后面在master节点初始化集群时会报错,内存不够),node节点可以2G,CPU至少2个,硬盘至少30G网络要求࿱…...
Win10右键 nvidia rtx desktop manager 怎么删除(最新)
在更新了最新的 nvidia后原来的隐藏鼠标右键菜单后不行了,新方法如下: 步骤一:在键盘“WINR”键同时操作下,启动运行框,在框内输入“regedit”,打开深度系统win7 的注册表编辑器。 步骤二:为防…...

MySQL加密的几种常见方式
MySQL提供了多种加密方式来保护数据的安全性。下面是几种常见的MySQL加密方式: 密码加密: MySQL5.7及以上版本使用SHA-256算法对密码进行加密。这种加密方式更安全,可以防止密码泄露。 之前的MySQL版本使用SHA-1算法进行密码加密。这种加密方…...

Android文字识别-阿里云OCR调用
0,阿里云OCR有在线识别接口,直接用httpPOST调用就能实现,开发起来很快捷。识别率还蛮好,摄像头斜着拍也能识别出来。实测识别时间单次在2s左右,普通使用使能满足需求的。 1,在阿里云页面先注册申请免费试用…...
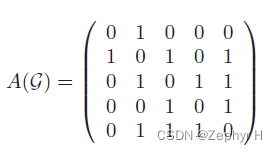
度矩阵、邻接矩阵
度矩阵(degree matrix) 度矩阵是对角阵,对角上的元素为各个顶点的度,顶点vi的度表示和该顶点相关联的变得数量。 在无向图中,顶点vi的度d(vi)N(i)(即与顶点相连的边的数目)有向图中࿰…...
20个经典巧妙电路合集
1、防反接保护(二极管) 在实际电子设计中,防反接保护电路非常重要,不要觉得自己肯定不会接错,实际上无论多么小心,还是会犯错误...... 最简单的就是利用二极管了,利用二极管的单向导电性&#…...
2023全国大学生数学建模ABCDE选题建议,思路模型,小白要怎么选?难度怎么样
首先最重要的,难度C<B<A,D、E题推荐选E题 大家可以查看我们的视频讲解,在这里:【2023全国大学生数学建模竞赛选题建议,难度分析,小白应该怎么选】 https://b23.tv/S6O26uc 选题建议视频播放b23.t…...

【力扣每日一题】2023.9.5 从两个数字数组里生成最小数字
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们两个数字数组,要我们用这两个数组里的元素组成一个数字,这个数字里需要同时拥有两个数组里的至少一个元…...
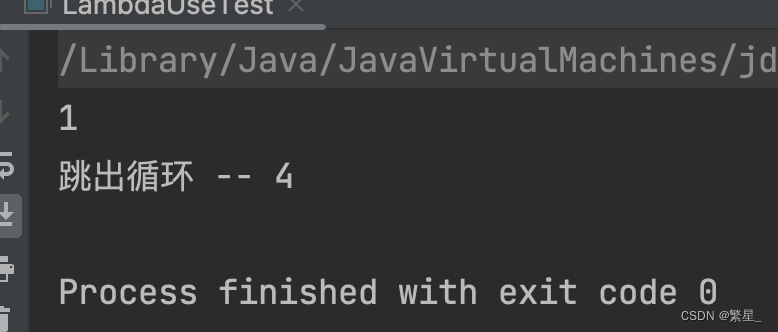
跳出Lambda表达式forEach()循环解决思路
背景 在一次需求开发时,发现使用Lambda的forEach()跳不出循环。如下示例代码,想在遍历满足条件时跳出循环。 public static void main(String[] args) {List<Integer> list Arrays.asList(1, 4, 5, 7, 9, 11);list.forEach(e -> {if (e % 2 …...

2023年度AWS SAP直冲云霄训练营学习分享
AWS在公有云市场一直处于行业领先地位,其培训认证体系也是非常的完善的。而且经常在国内组织一些技术论坛,技术分享,公开课,训练营等技术活动。 AWS训练营适合希望学习和考取AWS助理级架构师/专家级架构师(AWS SAA/AW…...
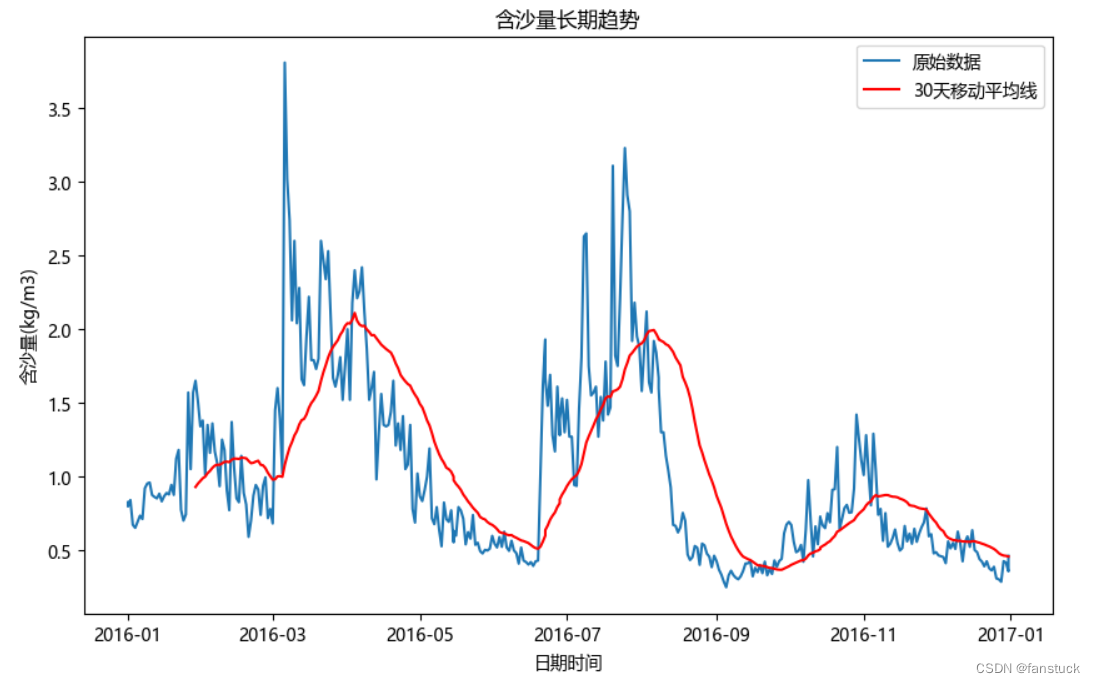
2023高教社杯 国赛数学建模E题思路 - 黄河水沙监测数据分析
1 赛题 E 题 黄河水沙监测数据分析 黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变 化和人民生活的影响, 以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾 等方面都具有重要的理论指导意义。 附件 1 给出了位…...

06_快速入门案例实战之电商网站商品管理:集群健康检查,文档CRUD
document数据格式电商网站商品管理案例:背景介绍简单的集群管理商品的CRUD操作(document CRUD (3) 集群的管理 1.快速检查集群的健康状态: cat api 可以查看es中各种各样的数据 GET /_cat/health?v epoch timestamp cluster status node…...

机车整备场数字孪生 | 图扑智慧铁路
机车整备场是铁路运输系统中的重要组成部分,它承担着机车的维修、保养和整备工作,对保障铁路运输的运维和安全起着至关重要的作用。 随着铁路运输的发展、机车技术的不断进步,以及数字化转型的不断推进,数字孪生技术在机车整备场…...

Fair|Fur —— Geometry Nodes
目录 Groom Blend Groom Fetch Groom Pack Groom Unpack Groom Switch Guide Advect Guide Collide With VDB Guide Deform Guide Draw Guide Groom Guide Group Guid Grow to Surface Guide Initialize Guide Mask Guide Partition Guide Process Guide Skin…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
