React三属性之:props
作用
将父组件的参数传递给子组件
父组件
import './App.css';
import React from 'react';
import PropsTest from './pages/propsTest'
class App extends React.Component{render(){return(<div><h2>App组件</h2><PropsTest obj={{name:'王惊涛',age:27}}></PropsTest></div>)}
}export default App;//组件上的obj={{name:'王惊涛',age:27}},传递的就是props参数子组件
import React from "react";
class PropsTest extends React.Component{render(){return(<div><h4>propsTest子组件</h4><p>名字{this.props.obj.name}</p><p>年龄{this.props.obj.age}</p></div>)}
}
export defaul效果如下

相关文章:

React三属性之:props
作用 将父组件的参数传递给子组件 父组件 import ./App.css; import React from react; import PropsTest from ./pages/propsTest class App extends React.Component{render(){return(<div><h2>App组件</h2><PropsTest obj{{name:王惊涛,age:27}}>…...

大数据安全 | (一)介绍
目录 📚大数据安全 🐇大数据安全内涵 🐇大数据安全威胁 🐇保障大数据安全 ⭐️采集环节安全技术 ⭐️存储环节安全技术 ⭐️挖掘环节安全技术 ⭐️发布环节安全技术 🐇大数据用于安全 📚隐私及其…...

软件工程的概念及其重要性
软件工程是指将工程原理和方法应用于软件开发过程的学科,涉及软件的设计、开发、测试、维护和管理等各个阶段。它旨在提高软件开发的效率和质量,并确保软件满足用户的需求和预期。 软件工程的重要性体现在以下几个方面: 提高开发效率&#x…...
[足式机器人]Part3 变分法Ch01-2 数学预备知识——【读书笔记】
本文仅供学习使用 本文参考: 《变分法基础-第三版》老大中 《变分学讲义》张恭庆 《Calculus of Variations of Optimal Control Theory》-变分法和最优控制论-Daneil Liberzon Ch01-2 数学基础-预备知识1 1.3.2 向量场的通量和散度1.3.3 高斯定理与格林公式 1.3.2 …...

【嵌入式开发 Linux 常用命令系列 7.1 -- awk 过滤列中含有特定字符的行】
文章目录 awk 过滤列中字符串 上篇文章:嵌入式开发 Linux 常用命令系列 7 – awk 常用方法详细介绍 awk 过滤列中字符串 cat test.log | awk -F $31 {print $0}说明: -F 以什么分隔列,这里是以空格为分隔符;$3代表第3列;$3…...

前端(十六)——Web应用的安全性研究
🙂博主:小猫娃来啦 🙂文章核心:Web应用的安全性研究 文章目录 概述常见前端安全漏洞XSS(跨站脚本攻击)CSRF(跨站请求伪造) 点击劫持安全性验证与授权用户身份验证授权与权限管理 安全…...

无涯教程-JavaScript - BIN2HEX函数
描述 BIN2HEX函数将二进制数转换为十六进制。 语法 BIN2HEX (number, [places])争论 Argument描述Required/Optionalnumber 您要转换的二进制数。 数字不能超过10个字符(10位)。数字的最高有效位是符号位。其余的9位是幅度位。 负数使用二进制补码表示。 Requiredplaces 要…...
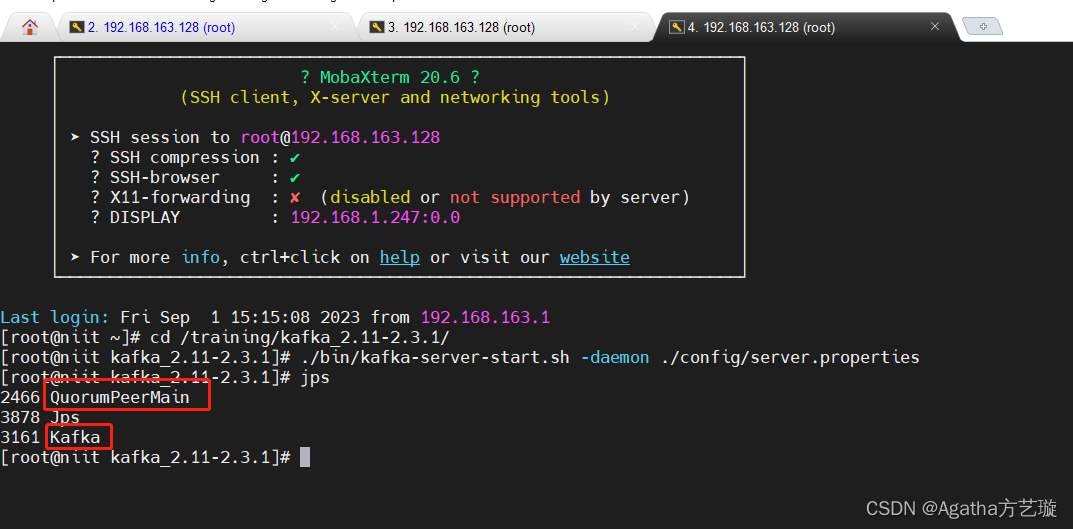
Kafka环境搭建与相关启动命令
一、Kafka环境搭建 点击下载kafka_2.11-2.3.1.tgz文件链接 1、上传kafka_2.11-2.3.1.tgz,解压kafka_2.11-2.3.1.tgz,得到kafka_2.11-2.3.1文件夹 1)上传 #使用mobaxterm将 kafka_2.11-2.3.1.tgz 传入tools文件夹 #用下面代码进入tools文件…...
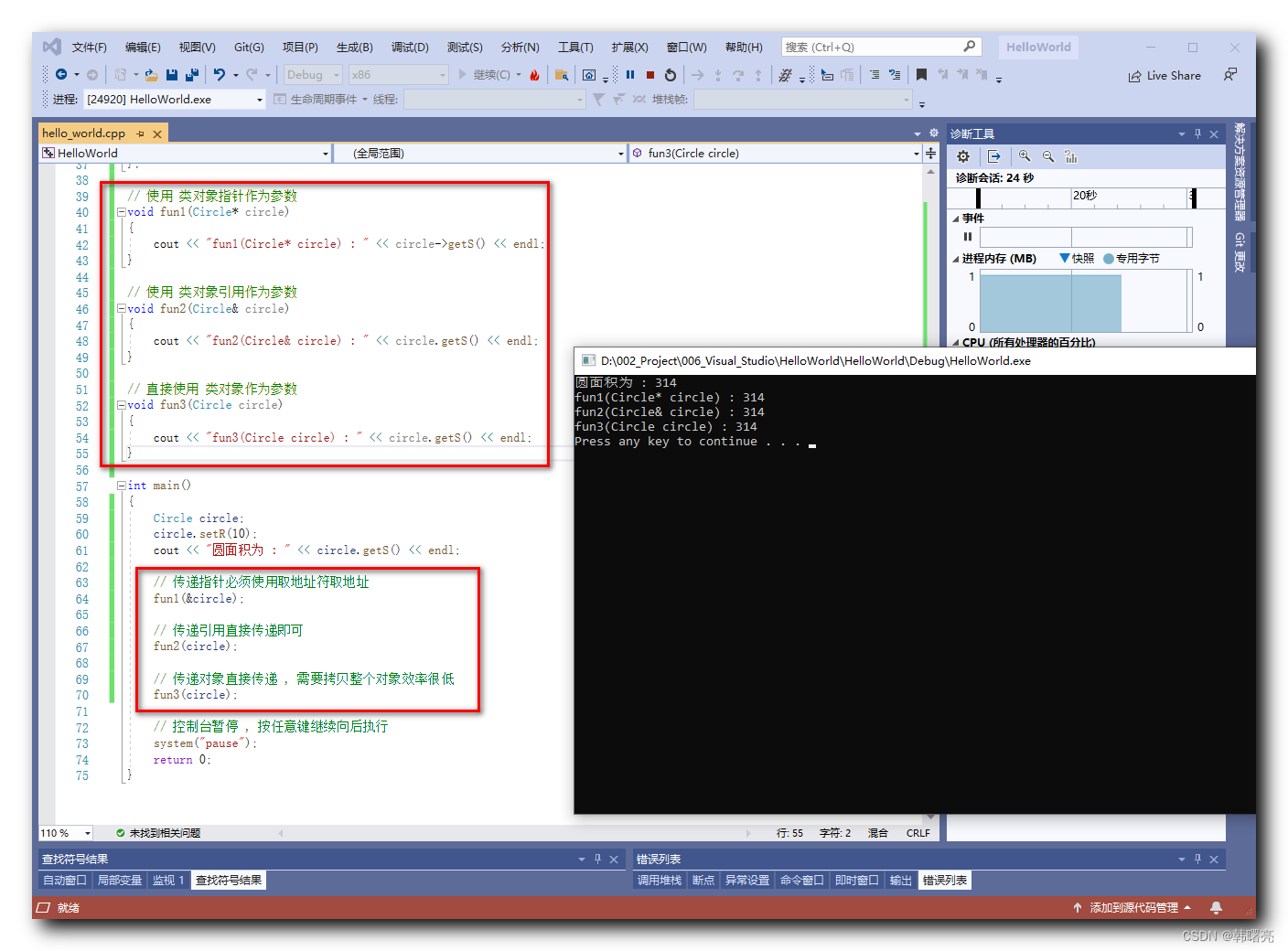
【C++】类的封装 ② ( 封装最基本的表层概念 | 类对象作为参数传递的几种情况 )
文章目录 一、类的封装 : 将数据和方法封装到一个类中1、封装最基本的表层概念2、代码分析 - 基本封装3、代码分析 - 类对象作为参数传递的几种情况 ( 指针 / 引用 / 直接 )4、完整代码示例 一、类的封装 : 将数据和方法封装到一个类中 1、封装最基本的表层概念 将数据和方法封…...

Linux上安装FTP
1、登录FTP,执行安装命令 yum -y install vsftpd 2、启动FTP服务器,设置开启自启动 systemctl enable vsftpd.service systemctl start vsftpd.service systemctl status vsftpd.service #查看状态, 显示active说明FTP启动成功 3、修改FTP配置文件/et…...
)
C/C++使用GDAL库编程窍门之——通用可移植性库(Common Portability Library, CPL)
C/C使用GDAL库编程窍门之——通用可移植性库(Common Portability Library, CPL) CPL简介 GDAL全称地理空间数据抽象库(Geospatial Data Abstraction Library),是一个强大的地理栅格空间数据转换库,支持众…...
 宏定义)
Linux container_of() 宏定义
container_of 宏 今天遇到了一段这样的代码,大致意思是 通过该struct结构体变量的成员的地址来反推该struct结构体变量的地址 并且用到了内核的宏,container_of() static inline struct nova_inode_info *NOVA_I(struct inode *inode) {return container…...

详解python中的序列类型---列表list
概述 列表类型是包含0个或多个元素的有序序列,属于序列类型。列表可以进行元素的增加、删除、替换、查找等操作。列表没有长度限制,无素类型可以不同,不需要预定长度。 列表类型用中括号[]表示,也可以通过list(x)函数将集合或字…...

Unity 引擎中国版 “团结引擎” 发布
导读Unity 官方宣布,Unity 中国正式推出 Unity 中国版引擎 —— 团结引擎,同时也开启了 Unity 中国本土化进程的全新篇章。作为推动团结引擎落地的核心人物,Unity 中国 CEO 张俊波称致力于将其打造为一款更懂中国开发者的引擎。 团结引擎以 U…...
MindsDB为许多不支持内置机器学习的数据库带来了机器学习功能
选择平台的首要原则是“靠近数据”,让代码靠近数据是保持低延迟的必要条件。 机器学习,特别是深度学习往往会多次遍历所有数据(遍历一次被称为一个epoch)。对于非常大的数据集来说,理想的情况是在存储数据的地方建立模型,这样就不需要大量的数据传输。目前已经有部分数据…...

世界级黑客丨电脑犯罪界的汉尼拔
被美国FBI称为电脑界的汉尼拔的人,有什么样的故事? 这个人就是世界级黑客凯文李波尔森,他在早期是正儿八经的黑客,他在17岁的时候就使用TRS-80电脑攻入美国国防部的高等研究计划署网络,但是当时他进去啥也没干&#x…...
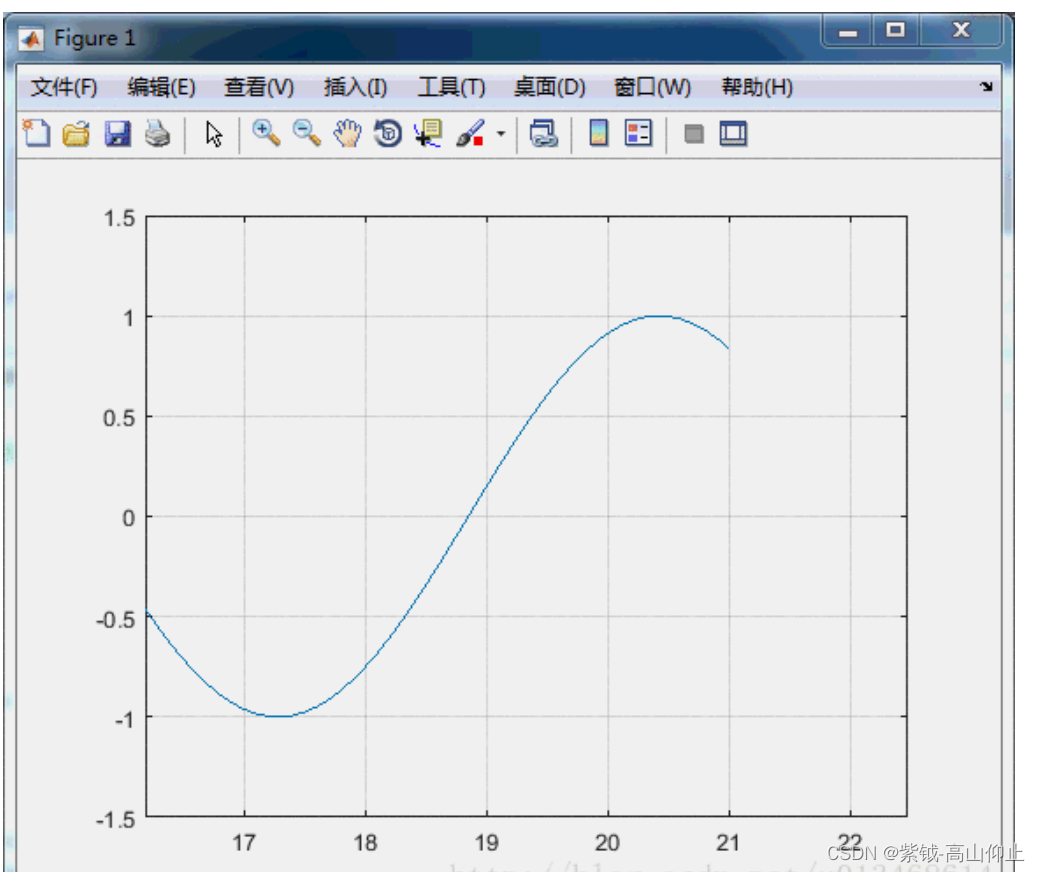
【Matlab】Matlab实现数据的动态显示方法
Matlab实现数据的动态显示方法 主要为大家详细介绍了Matlab使用Plot函数实现数据动态显示方法,具有一定的参考价值,感兴趣的小伙伴们可 以参考一下 对于真实系统或者仿真平台,数据是增量式的产生的。Matlab除了强大的矩阵运算外,还…...
【Android】SDK安装及配置
一、下载SDK Tools https://www.androiddevtools.cn 以windows10系统为例,下载压缩版直接解压即可。 二、安装SDK Tools 解压后双击运行SDK Manager.exe 一般根据默认推荐安装即可。 如果无法打开SDK Manager,可以参考:https://blog.cs…...
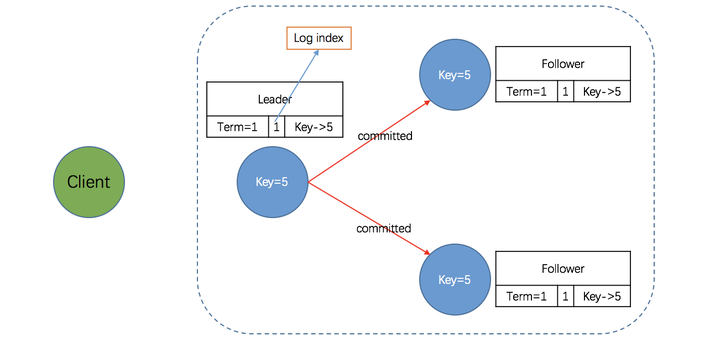
ETCD详解
一、etcd概念 ETCD 是一个高可用的分布式键值key-value数据库,可用于服务发现。 ETCD 采用raft 一致性算法,基于 Go语言实现。 etcd作为一个高可用键值存储系统,天生就是为集群化而设计的。由于Raft算法在做决策时需要多数节点的投票&…...
hook)
React笔记(五)hook
一、函数组件 1、函数组件的创建 函数组件:使用JS的函数(或箭头函数)创建的组件称为函数组件,函数组件有如下约定 函数名称必须以大写字母开头 函数组件必须有返回值,返回JSX表达式 渲染函数组件:用函数…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
