【Matlab】Matlab实现数据的动态显示方法
Matlab实现数据的动态显示方法
主要为大家详细介绍了Matlab使用Plot函数实现数据动态显示方法,具有一定的参考价值,感兴趣的小伙伴们可
以参考一下
对于真实系统或者仿真平台,数据是增量式的产生的。Matlab除了强大的矩阵运算外,还具有强大的数据可视化库。由于静态
画图的方法较多,本文只针对增量式数据流的动态显示。本文主要介绍几种Matlab实现数据的动态显示方法。方法主要有两
种:
hold on
set函数与drawnow函数组合
hold on
set函数与drawnow函数组合
hold on 方法方
- 方法介绍
此种方法比较原始,适合于即时数据,原理是先画上一帧,接着保留原始图像,追加下一幀图像,此种方式比较繁琐,涉及画
图细节,并且没有完整并连续的Line对象数据。此种方法需要注意的地方是,若想生成连续的线图,则每次plot至少两个点,
原理大家都应该理解,两点一线嘛!如果想每次一个点增量式的画图,则线型选择’.'。 - 代码与图例
t=0;
m=0;
t1=[0 0.1]; %若为'-'至少同时输入两个点,两点一线嘛!!!而'.'则不用
m1=sin(t1);
p = plot(t1,m1,'-b','MarkerSize',5);
x=-1.5*pi;
axis([x x+2*pi -1.5 1.5]);
grid on;
for i=1:1000
hold on
t=0.1*i; %下一个点
m=t-floor(t);
t1=t1+0.1; %下一段线
m1=sin(t1);
p = plot(t1,m1,'-b','MarkerSize',5);
x=x+0.1;
axis([x x+2*pi -1.5 1.5]);
pause(0.01);
end

set函数与 函 drawnow函数组合 函
3. 方法介绍
这种模式比较适合画动画,效率比较高,刷新闪烁小,适合即时数据,最终的Line结构数据完整。
了解此方法之前要搞清楚 Plot函数的原型是什么: 每个Plot由一个句柄维护,而可以通过set函数对该句柄对应的plot参数在线
的更新,若在线更新plot的数据,则可实现动态显示的效果。
最后使用drawnow函数对plot进行刷新。
4. 代码与图例
t=[0]
m=sin(t)
p = plot(t,m,'EraseMode','background','MarkerSize',5);
x=-1.5*pi;
axis([x x+2*pi -1.5 1.5]);
grid on;
for i=1:1000
t=[t 0.1*i];
m=[m sin(0.1*i)];
set(p,'XData',t,'YData',m)
drawnow
x=x+0.1;
axis([x x+2*pi -1.5 1.5]);
pause(0.01);
end
总结
本文介绍了两种实现即时数据可视化的方法。也就是看上去的动态显示效果。分别给出了两种方法的原理介绍和示例程序与图
例。相信这两个简单的例子经过你的运用可以变幻出多姿多彩的数据可视化效果。
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持我们,点赞关注!
相关文章:

【Matlab】Matlab实现数据的动态显示方法
Matlab实现数据的动态显示方法 主要为大家详细介绍了Matlab使用Plot函数实现数据动态显示方法,具有一定的参考价值,感兴趣的小伙伴们可 以参考一下 对于真实系统或者仿真平台,数据是增量式的产生的。Matlab除了强大的矩阵运算外,还…...
【Android】SDK安装及配置
一、下载SDK Tools https://www.androiddevtools.cn 以windows10系统为例,下载压缩版直接解压即可。 二、安装SDK Tools 解压后双击运行SDK Manager.exe 一般根据默认推荐安装即可。 如果无法打开SDK Manager,可以参考:https://blog.cs…...
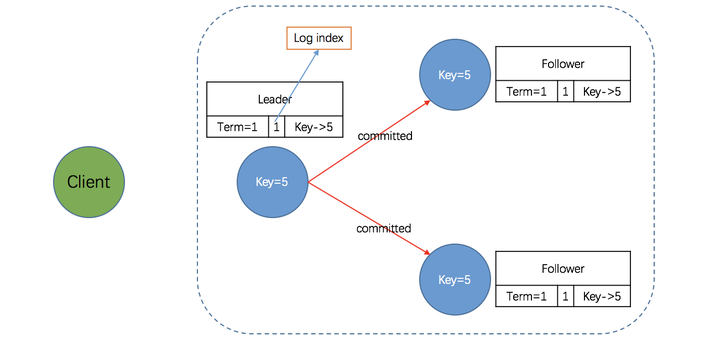
ETCD详解
一、etcd概念 ETCD 是一个高可用的分布式键值key-value数据库,可用于服务发现。 ETCD 采用raft 一致性算法,基于 Go语言实现。 etcd作为一个高可用键值存储系统,天生就是为集群化而设计的。由于Raft算法在做决策时需要多数节点的投票&…...
hook)
React笔记(五)hook
一、函数组件 1、函数组件的创建 函数组件:使用JS的函数(或箭头函数)创建的组件称为函数组件,函数组件有如下约定 函数名称必须以大写字母开头 函数组件必须有返回值,返回JSX表达式 渲染函数组件:用函数…...

vue3中使用viewerjs实现图片预览效果
vue3中使用viewerjs实现图片预览效果 1、前言2、实现效果3、在vue3项目中使用viewer.js3.1 安装3.2 在main.js中引入3.3 组件中使用 1、前言 viewer.js是一款开源的图片预览插件,功能十分强大: 支持移动设备触摸事件支持响应式支持放大/缩小支持旋转(类…...

Erlang:Linux下使用observer、debugger进行调试
之前写了一篇文章Erlang:使用observer连接远程服务器进行调试,内容是绕过Linux服务器缺失’wxe_driver.so’的wxWidgets环境,启动observer远程连接实现observer调试。 本文则讨论在Linux环境下通过编译安装的方式,保证wxWidgets环境可用性&am…...
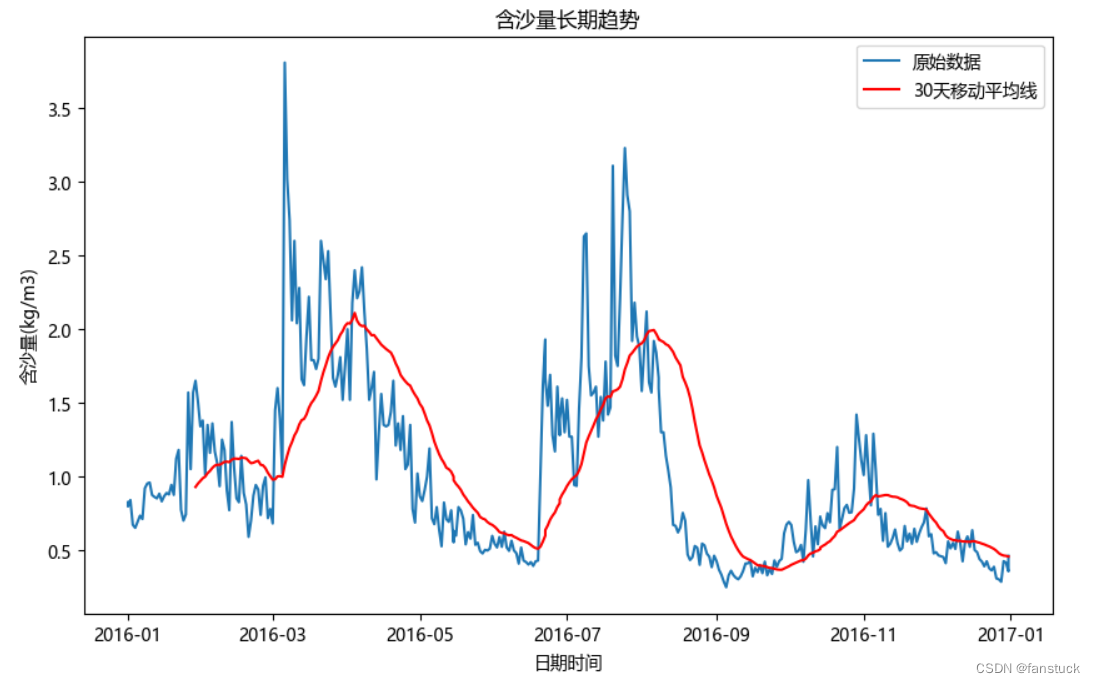
2023 年高教社杯全国大学生数学建模竞赛-E 题 黄河水沙监测数据分析详解+思路+Python代码
2023 年高教社杯全国大学生数学建模竞赛-E 题 黄河水沙监测数据分析 十分激动啊啊啊题目终于出来了!!官网6点就进去了结果直接卡死现在才拿到题目,我是打算A-E题全部做一遍。简单介绍一下我自己:博主专注建模四年,参与…...

一生一芯10——verilator v5.008环境搭建
搜索 verilator 官网,得到网址如下: https://www.veripool.org/verilator/ 点击download 找到 git quick install 可以看到git快捷安装所需命令行 可以看到,需要预先安装下面的包文件,去掉前面的#注释符号进行安装 直接进行下面…...

信息化发展27
关键技术一云安全技术 云安全研究主要包含: 一是云计算技术本身的安全保护工作, 涉及相应的数据完整性及可用性、隐私保护性以及服务可用性等方面的内容; 二是借助于云服务的方式来保障客户端用户的安全防护需求, 通过云计算技术…...

leetcode做题笔记129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。…...

任务管理系统所需功能概述
"任务管理需要有哪些功能?清晰的任务创建与编辑、智能分类和标签系统、提醒与通知功能、进度跟踪与报告、协作与共享功能、集成与兼容性。" 一款优秀的任务管理工具可以帮助我们有效地规划、执行和监控各项任务,提高工作效率。本文将探讨一款理…...

一文学会K8s集群搭建
环境准备 节点数量:2台虚拟机 centos7硬件配置:master节点内存至少3G(2G后面在master节点初始化集群时会报错,内存不够),node节点可以2G,CPU至少2个,硬盘至少30G网络要求࿱…...
Win10右键 nvidia rtx desktop manager 怎么删除(最新)
在更新了最新的 nvidia后原来的隐藏鼠标右键菜单后不行了,新方法如下: 步骤一:在键盘“WINR”键同时操作下,启动运行框,在框内输入“regedit”,打开深度系统win7 的注册表编辑器。 步骤二:为防…...

MySQL加密的几种常见方式
MySQL提供了多种加密方式来保护数据的安全性。下面是几种常见的MySQL加密方式: 密码加密: MySQL5.7及以上版本使用SHA-256算法对密码进行加密。这种加密方式更安全,可以防止密码泄露。 之前的MySQL版本使用SHA-1算法进行密码加密。这种加密方…...

Android文字识别-阿里云OCR调用
0,阿里云OCR有在线识别接口,直接用httpPOST调用就能实现,开发起来很快捷。识别率还蛮好,摄像头斜着拍也能识别出来。实测识别时间单次在2s左右,普通使用使能满足需求的。 1,在阿里云页面先注册申请免费试用…...
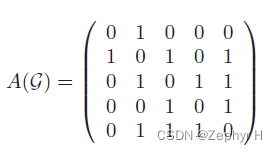
度矩阵、邻接矩阵
度矩阵(degree matrix) 度矩阵是对角阵,对角上的元素为各个顶点的度,顶点vi的度表示和该顶点相关联的变得数量。 在无向图中,顶点vi的度d(vi)N(i)(即与顶点相连的边的数目)有向图中࿰…...
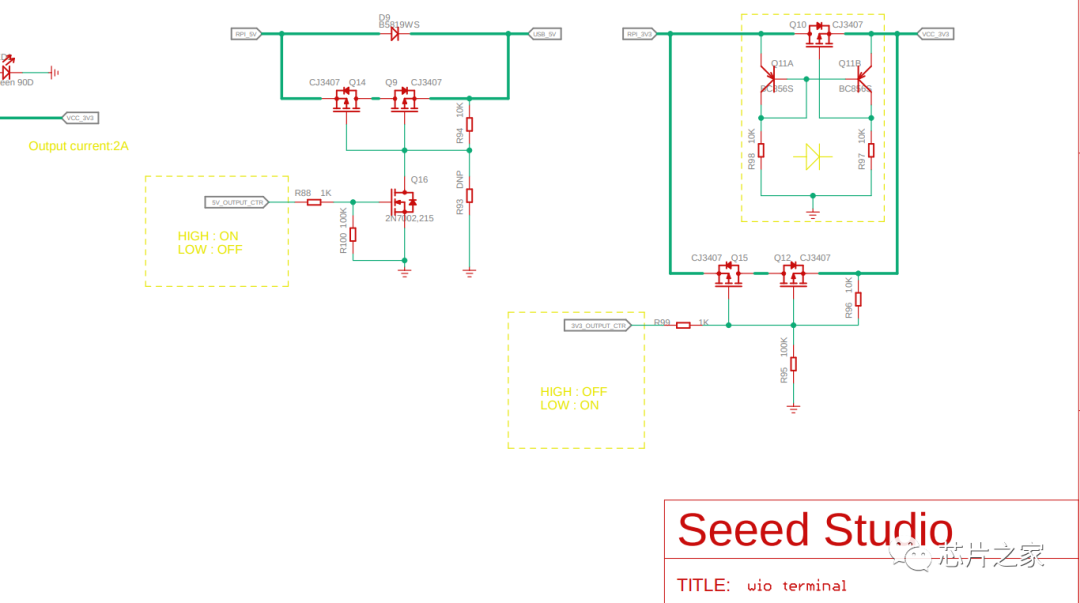
20个经典巧妙电路合集
1、防反接保护(二极管) 在实际电子设计中,防反接保护电路非常重要,不要觉得自己肯定不会接错,实际上无论多么小心,还是会犯错误...... 最简单的就是利用二极管了,利用二极管的单向导电性&#…...
2023全国大学生数学建模ABCDE选题建议,思路模型,小白要怎么选?难度怎么样
首先最重要的,难度C<B<A,D、E题推荐选E题 大家可以查看我们的视频讲解,在这里:【2023全国大学生数学建模竞赛选题建议,难度分析,小白应该怎么选】 https://b23.tv/S6O26uc 选题建议视频播放b23.t…...

【力扣每日一题】2023.9.5 从两个数字数组里生成最小数字
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们两个数字数组,要我们用这两个数组里的元素组成一个数字,这个数字里需要同时拥有两个数组里的至少一个元…...
跳出Lambda表达式forEach()循环解决思路
背景 在一次需求开发时,发现使用Lambda的forEach()跳不出循环。如下示例代码,想在遍历满足条件时跳出循环。 public static void main(String[] args) {List<Integer> list Arrays.asList(1, 4, 5, 7, 9, 11);list.forEach(e -> {if (e % 2 …...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
