JDK源码剖析之PriorityQueue优先级队列
写在前面
版本信息:
JDK1.8
PriorityQueue介绍
在数据结构中,队列分为FIFO、LIFO 两种模型,分别为先进先出,后进后出、先进后出,后进先出(栈) 而一切数据结构都是基于数组或者是链表实现。
在Java中,定义了Queue接口,接口中定义了CRUD的基本方法。分别add、offer、remove、poll等等,而PriorityQueue 实现此接口实现了基本的CRUD的同时拥有了自己的特性,从名字来看也能知道是优先级队列 : 保持队列头部节点是整条队列中永远是最小或者最大的节点,其实现原理就是一个小顶堆或者大顶堆。上文提及到一切数据结构都是基于数组或者是链表实现,而这里使用了数组实现。
public class PriorityQueue<E> extends AbstractQueue<E>implements java.io.Serializable {transient Object[] queue; // 由数组实现
}public abstract class AbstractQueue<E>extends AbstractCollection<E>implements Queue<E> {}小顶堆和大顶堆介绍
从上文描述了PriorityQueue的底层实现是小顶堆或者大顶堆,那么在看源码之前,我们需要先明白小顶堆和大顶堆如何实现~
小顶堆:一颗完全二叉树,其中任意父节点都要小于左右子节点,所以树的根节点是整棵树的最小节点
大顶堆:一颗完全二叉树,其中任意父节点都要大于左右子节点,所以树的根节点是整棵树的最大节点
Comparable和Comparator区别
在看PriorityQueue源码之前还需要分析Comparable和Comparator区别。
Comparable:类需要实现此接口,重写compareTo方法,在compareTo方法中定义比较逻辑,使用时把类强转成Comparable调用compareTo方法,把比较对象传入。所以侵入性比较强,与业务代码强耦合。
Comparator:这个就是一个比较器,只需要把A比较对象和B比较对象都传入即可,不需要于业务代码强耦合
PriorityQueue添加元素源码分析
下文直接把PriorityQueue叫成小顶堆
我们直接从offer方法入手~
public boolean offer(E e) {if (e == null)throw new NullPointerException();modCount++; // 用于检测是否并发// 因为size从0开始,所以size的值就是数组的索引值。int i = size;// 是否需要扩容if (i >= queue.length)grow(i + 1); // 为下次索引+1size = i + 1;// 如果是第一个,那么就直接占用数组第一个元素即可,// 因为不管是小顶堆还是大堆堆第一个都直接插入。if (i == 0)queue[0] = e;else// 非第一个节点,此时就需要调整siftUp(i, e);return true;
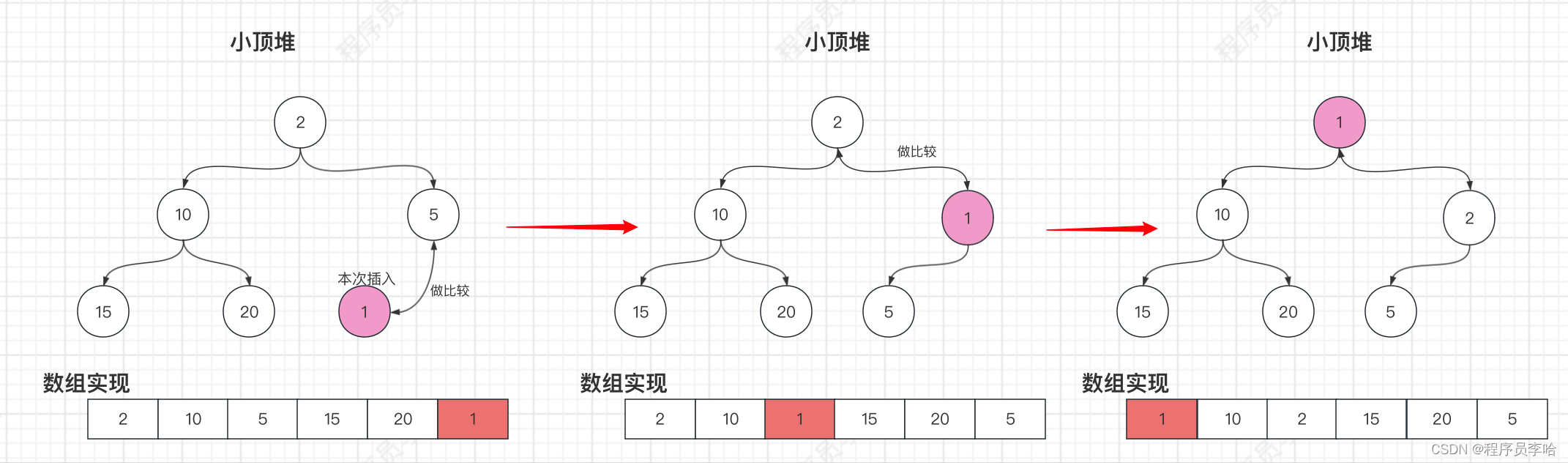
}这里的逻辑比较简单,因为这里使用数组实现的小顶堆(也即使用数组实现完全二叉树),而小顶堆的第一个节点是最小的,所以当0索引直接插入即可,非0索引就需要调整小顶堆。这里应该有很多读者是第一次见数组实现二叉树,所以这里把上文的二叉树进行扩展,把数组部分画上去。

在看 siftUp调整方法前,我们看一下grow扩容方法, 因为里面有一个思路大家可以学习~
private void grow(int minCapacity) {int oldCapacity = queue.length;// 容量小于64时,扩容为 oldCapacity + oldCapacity +2 // 容量大于64,扩容为 oldCapacity + oldCapacity/2// 等同于,在容量小的时候,每次扩容大一些,当达到64这个阈值后,扩容小一些,要不然空间会太浪费了~int newCapacity = oldCapacity + ((oldCapacity < 64) ?(oldCapacity + 2) :(oldCapacity >> 1));if (newCapacity - MAX_ARRAY_SIZE > 0)newCapacity = hugeCapacity(minCapacity);// 数组拷贝迁移。queue = Arrays.copyOf(queue, newCapacity);
}
在每次扩容的时候,会去判断,当前容量是否大于64,如果小于64就直接 原大小 * 2 + 2 扩容,如果大于64以后直接 原大小 + 原大小/2 扩容。目的是为了在容量小的时候扩容大一些,减少扩容次数。在容量达到64阈值后,扩容小一些,减少内存浪费。
下面开始讲解siftUp调整方法
private void siftUp(int k, E x) {// 用户是否传入comparator比较器if (comparator != null)siftUpUsingComparator(k, x);else// 没传入就使用Comparable// 此时类需要实现Comparable接口siftUpComparable(k, x);
}这里讲解siftUpComparable方法,本质上两个方法没任何区别~
private void siftUpComparable(int k, E x) {Comparable<? super E> key = (Comparable<? super E>) x;while (k > 0) {// 拿到父节点// 因为是使用数组实现的一颗完全二叉树,所以直接-1 右移即可拿到当前插入节点的父节点int parent = (k - 1) >>> 1;Object e = queue[parent];// 与父节点做比较。if (key.compareTo((E) e) >= 0)// 达到用户的预期比较就直接break,要不然继续往父节点的父节点继续做比较,直到根节点break;// 没达到预期,所以把父节点插入到本次插入的节点的位置。queue[k] = e;// 拿到父节点的索引,继续往父节点的父节点做比较。k = parent;}// 插入queue[k] = key;
}这里光看注释,肯定是看不明白的,所以以画图+注释来理解吧~
PriorityQueue获取元素源码分析
直接从poll方法入手~
public E poll() {if (size == 0)return null;// 拿到最后一个节点的索引值。int s = --size;modCount++;// 因为第一个是小顶堆或者大顶堆要的数据。E result = (E) queue[0];// 拿到最后一节点E x = (E) queue[s];queue[s] = null; // help gcif (s != 0)// 调整siftDown(0, x);return result;
}因为小顶堆或者大顶堆都是拿第一个元素,所以这里拿出第一个元素。但是每次拿完就需要调整小顶堆(调整完全二叉树),所以看到siftDown方法。
private void siftDown(int k, E x) {if (comparator != null)siftDownUsingComparator(k, x);elsesiftDownComparable(k, x);
}本质上这两个方法没任何区别,所以继续看到siftDownComparable方法
// k为0
// x是最后一个节点。
private void siftDownComparable(int k, E x) {Comparable<? super E> key = (Comparable<? super E>)x;// 循环的次数// 是通过数组的大小 右移一位就可以知道树高了。int half = size >>> 1; while (k < half) {// 往下层找。int child = (k << 1) + 1; Object c = queue[child]; // 左子节点int right = child + 1; // 右子节点// 左右子节点比较,那个满足规范就作为父节点if (right < size &&((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)// 右节点满足于左节点c = queue[child = right];// 与最后一个节点比较后,达到预期直接退出if (key.compareTo((E) c) <= 0)break;// 替换queue[k] = c;// 下次循环的父节点k = child;}queue[k] = key;
}因为每次poll取走的是第一个元素,所以需要调整整个小顶堆,而第一个元素是小顶堆的根节点,所以需要调整小顶堆找到一个符合的元素作为根节点。从根节点的左右子节点开始比较,左右子节点比较出预期的节点就作为新的根节点。预期的节点作为下次比较的父节点,通过父节点再找到他的左右子节点做比较,周而复始,直到最后一个节点。
这里光看注释,肯定是看不明白的,所以以画图+注释来理解吧~

相关文章:

JDK源码剖析之PriorityQueue优先级队列
写在前面 版本信息: JDK1.8 PriorityQueue介绍 在数据结构中,队列分为FIFO、LIFO 两种模型,分别为先进先出,后进后出、先进后出,后进先出(栈) 而一切数据结构都是基于数组或者是链表实现。 在…...

TSINGSEE青犀AI视频分析/边缘计算/AI算法·人脸识别功能——多场景高效运用
旭帆科技AI智能分析网关可提供海量算法供应,涵盖目标监测、分析、抓拍、动作分析、AI识别等,可应用于各行各业的视觉场景中。同时针对小众化场景可快速定制AI算法,主动适配大厂近百款芯片,打通云/边/端灵活部署,算法一…...
算法_C++——最大连续 1 的个数 III)
力扣(LeetCode)算法_C++——最大连续 1 的个数 III
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 示例 1: 输入:nums [1,1,1,0,0,0,1,1,1,1,0], K 2 输出:6 解释:[1,1,1,0,0,1,1,1,1,1,1] 粗体数字…...

23062C++QT day2
封装一个结构体,结构体中包含一个私有数组,用来存放学生的成绩,包含一个私有变量,用来记录学生个数, 提供一个公有成员函数,void setNum(int num)用于设置学生个数 提供一个公有成员函数:void…...

React三属性之:props
作用 将父组件的参数传递给子组件 父组件 import ./App.css; import React from react; import PropsTest from ./pages/propsTest class App extends React.Component{render(){return(<div><h2>App组件</h2><PropsTest obj{{name:王惊涛,age:27}}>…...

大数据安全 | (一)介绍
目录 📚大数据安全 🐇大数据安全内涵 🐇大数据安全威胁 🐇保障大数据安全 ⭐️采集环节安全技术 ⭐️存储环节安全技术 ⭐️挖掘环节安全技术 ⭐️发布环节安全技术 🐇大数据用于安全 📚隐私及其…...

软件工程的概念及其重要性
软件工程是指将工程原理和方法应用于软件开发过程的学科,涉及软件的设计、开发、测试、维护和管理等各个阶段。它旨在提高软件开发的效率和质量,并确保软件满足用户的需求和预期。 软件工程的重要性体现在以下几个方面: 提高开发效率&#x…...
[足式机器人]Part3 变分法Ch01-2 数学预备知识——【读书笔记】
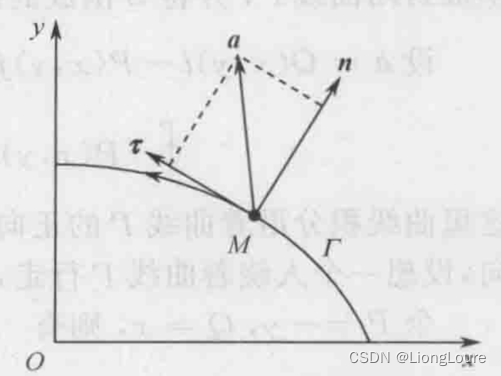
本文仅供学习使用 本文参考: 《变分法基础-第三版》老大中 《变分学讲义》张恭庆 《Calculus of Variations of Optimal Control Theory》-变分法和最优控制论-Daneil Liberzon Ch01-2 数学基础-预备知识1 1.3.2 向量场的通量和散度1.3.3 高斯定理与格林公式 1.3.2 …...

【嵌入式开发 Linux 常用命令系列 7.1 -- awk 过滤列中含有特定字符的行】
文章目录 awk 过滤列中字符串 上篇文章:嵌入式开发 Linux 常用命令系列 7 – awk 常用方法详细介绍 awk 过滤列中字符串 cat test.log | awk -F $31 {print $0}说明: -F 以什么分隔列,这里是以空格为分隔符;$3代表第3列;$3…...

前端(十六)——Web应用的安全性研究
🙂博主:小猫娃来啦 🙂文章核心:Web应用的安全性研究 文章目录 概述常见前端安全漏洞XSS(跨站脚本攻击)CSRF(跨站请求伪造) 点击劫持安全性验证与授权用户身份验证授权与权限管理 安全…...

无涯教程-JavaScript - BIN2HEX函数
描述 BIN2HEX函数将二进制数转换为十六进制。 语法 BIN2HEX (number, [places])争论 Argument描述Required/Optionalnumber 您要转换的二进制数。 数字不能超过10个字符(10位)。数字的最高有效位是符号位。其余的9位是幅度位。 负数使用二进制补码表示。 Requiredplaces 要…...
Kafka环境搭建与相关启动命令
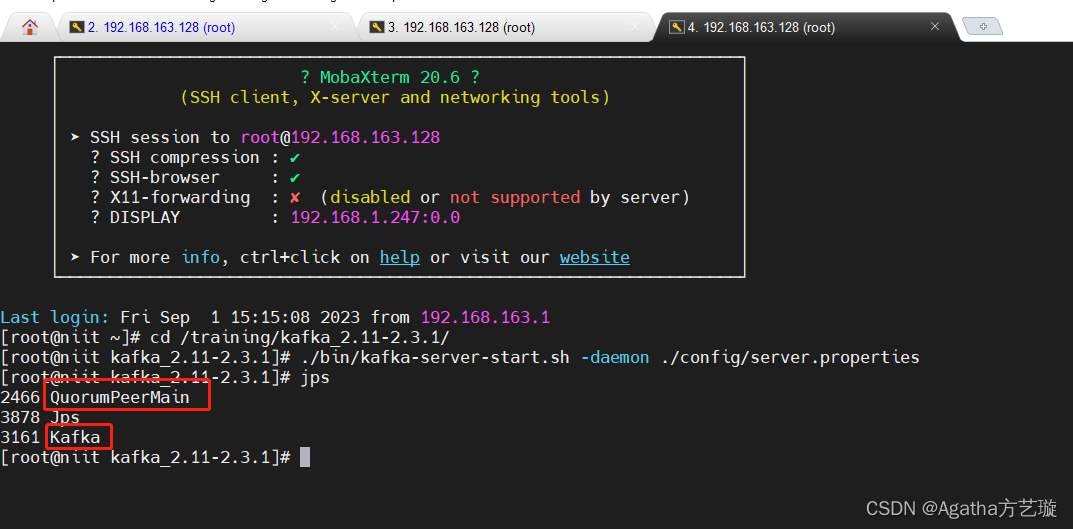
一、Kafka环境搭建 点击下载kafka_2.11-2.3.1.tgz文件链接 1、上传kafka_2.11-2.3.1.tgz,解压kafka_2.11-2.3.1.tgz,得到kafka_2.11-2.3.1文件夹 1)上传 #使用mobaxterm将 kafka_2.11-2.3.1.tgz 传入tools文件夹 #用下面代码进入tools文件…...
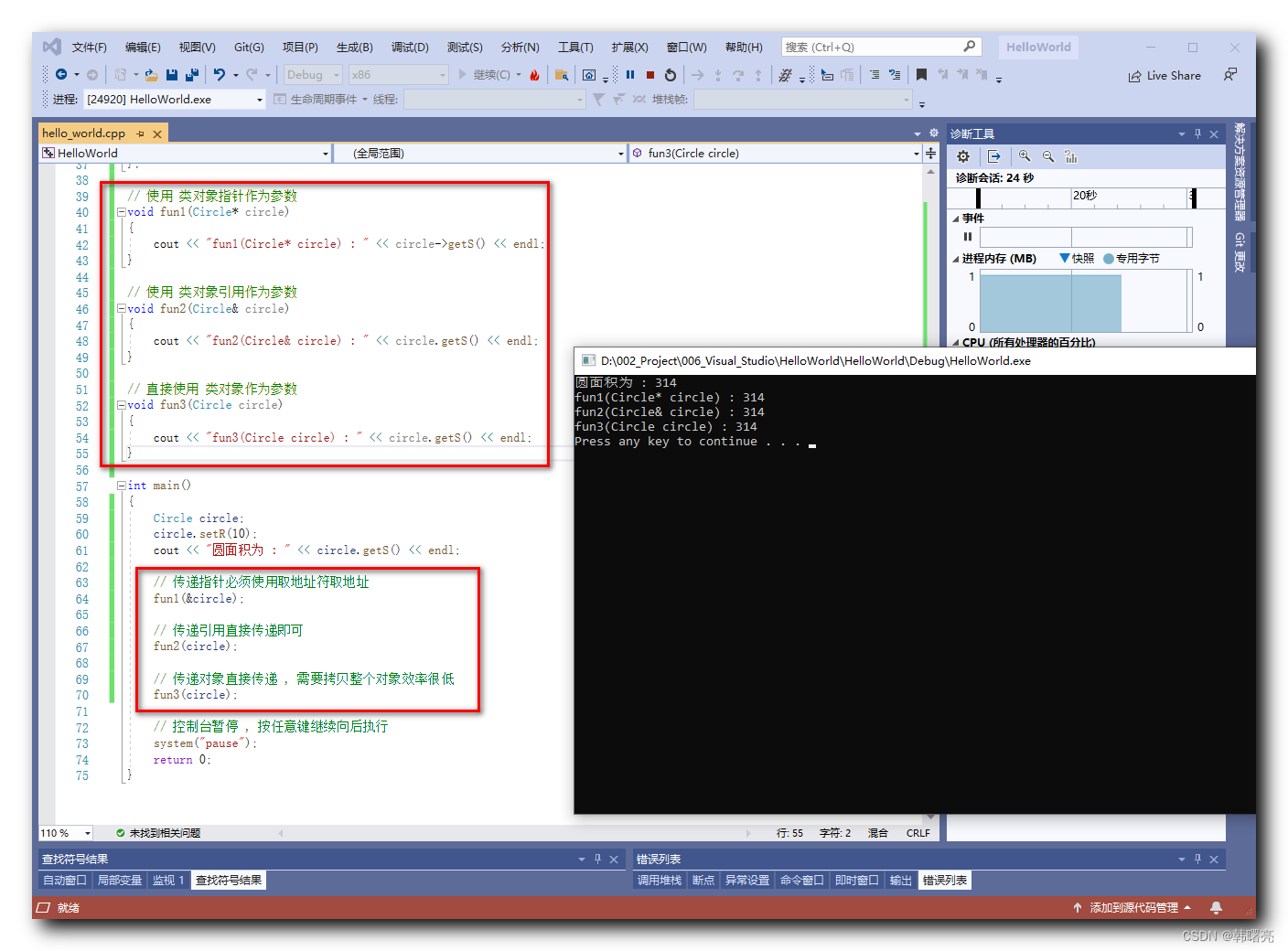
【C++】类的封装 ② ( 封装最基本的表层概念 | 类对象作为参数传递的几种情况 )
文章目录 一、类的封装 : 将数据和方法封装到一个类中1、封装最基本的表层概念2、代码分析 - 基本封装3、代码分析 - 类对象作为参数传递的几种情况 ( 指针 / 引用 / 直接 )4、完整代码示例 一、类的封装 : 将数据和方法封装到一个类中 1、封装最基本的表层概念 将数据和方法封…...

Linux上安装FTP
1、登录FTP,执行安装命令 yum -y install vsftpd 2、启动FTP服务器,设置开启自启动 systemctl enable vsftpd.service systemctl start vsftpd.service systemctl status vsftpd.service #查看状态, 显示active说明FTP启动成功 3、修改FTP配置文件/et…...
)
C/C++使用GDAL库编程窍门之——通用可移植性库(Common Portability Library, CPL)
C/C使用GDAL库编程窍门之——通用可移植性库(Common Portability Library, CPL) CPL简介 GDAL全称地理空间数据抽象库(Geospatial Data Abstraction Library),是一个强大的地理栅格空间数据转换库,支持众…...
 宏定义)
Linux container_of() 宏定义
container_of 宏 今天遇到了一段这样的代码,大致意思是 通过该struct结构体变量的成员的地址来反推该struct结构体变量的地址 并且用到了内核的宏,container_of() static inline struct nova_inode_info *NOVA_I(struct inode *inode) {return container…...

详解python中的序列类型---列表list
概述 列表类型是包含0个或多个元素的有序序列,属于序列类型。列表可以进行元素的增加、删除、替换、查找等操作。列表没有长度限制,无素类型可以不同,不需要预定长度。 列表类型用中括号[]表示,也可以通过list(x)函数将集合或字…...

Unity 引擎中国版 “团结引擎” 发布
导读Unity 官方宣布,Unity 中国正式推出 Unity 中国版引擎 —— 团结引擎,同时也开启了 Unity 中国本土化进程的全新篇章。作为推动团结引擎落地的核心人物,Unity 中国 CEO 张俊波称致力于将其打造为一款更懂中国开发者的引擎。 团结引擎以 U…...
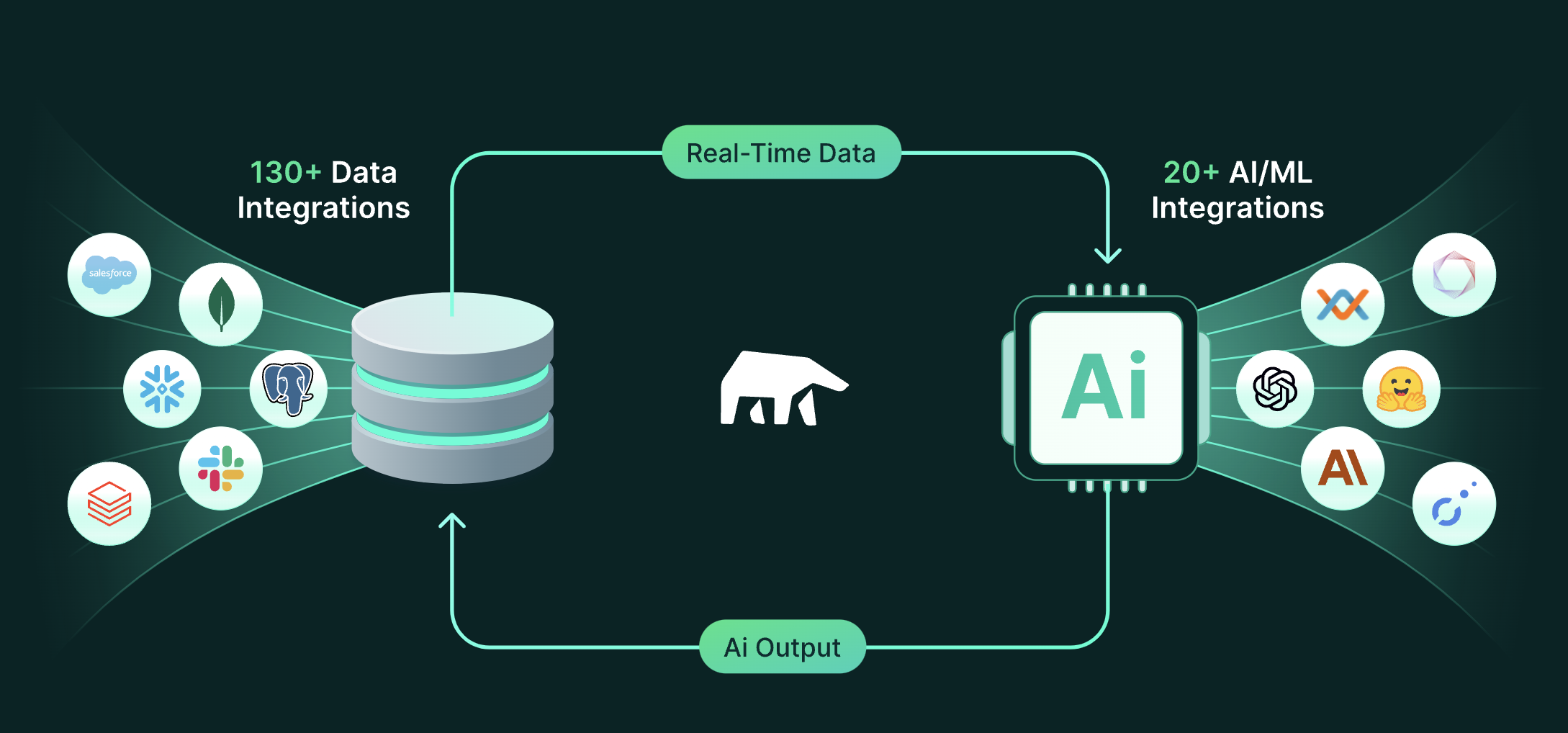
MindsDB为许多不支持内置机器学习的数据库带来了机器学习功能
选择平台的首要原则是“靠近数据”,让代码靠近数据是保持低延迟的必要条件。 机器学习,特别是深度学习往往会多次遍历所有数据(遍历一次被称为一个epoch)。对于非常大的数据集来说,理想的情况是在存储数据的地方建立模型,这样就不需要大量的数据传输。目前已经有部分数据…...

世界级黑客丨电脑犯罪界的汉尼拔
被美国FBI称为电脑界的汉尼拔的人,有什么样的故事? 这个人就是世界级黑客凯文李波尔森,他在早期是正儿八经的黑客,他在17岁的时候就使用TRS-80电脑攻入美国国防部的高等研究计划署网络,但是当时他进去啥也没干&#x…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

