最优化:建模、算法与理论(优化建模——2)
3.10 K-均值聚类
聚类分析是 统计学中的一个基本问题,其在机器学习,数据挖掘,模式识别和图像分析中有着重要应用。聚类不同于分类,在聚类问题中我们仅仅知道数据点本身,而不知道每个数据点具体的标签。聚类分析的任务就是将一些无标签的数据点按照某种相似度来进行归类,进而从数据点本身来学习其内蕴的类别特征。
给定 p p p维空间中的 n n n个数据点 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an,假定两个数据点之间的相似性可以通过其欧几里得距离来测量,我们的目标是将相似的点归为一类,同时将不相似的点区分开,为了简单起来我们假设类的个数为已知的,不妨记为 k k k,且同一个数据点只属于一个类,因此聚类问题就是要找 k k k个不相交的非空集合 S 1 , S 2 , ⋯ , S k S_1,S_2,\cdots,S_k S1,S2,⋯,Sk,使得
{ a 1 , a 2 , ⋯ , a n } = S 1 ∪ S 2 ∪ ⋯ ∪ S k \{a_1,a_2,\cdots,a_n\}=S_1\cup{S_2}\cup{\cdots}\cup{S_k} {a1,a2,⋯,an}=S1∪S2∪⋯∪Sk
且同类点之间的距离要足够近,为了在数学上描述"同类点之间的距离足够近",我们定义组内距离平方和为
W ( S 1 , S 2 , ⋯ , S k ) = ∑ i = 1 k ∑ a ∈ S i ∣ ∣ a − c i ∣ ∣ 2 (3.10.1) W(S_1,S_2,\cdots,S_k)=\sum_{i=1}^k\sum_{a{\in}S_i}||a-c_i||^2 \tag{3.10.1} W(S1,S2,⋯,Sk)=i=1∑ka∈Si∑∣∣a−ci∣∣2(3.10.1)
这里 c i c_i ci为第 i i i类数据点的中心,注意在问题中就假设了每类为非空的
定义好聚类标准后,就可以建议优化模型了。我们想要找到一个聚类方法,使得组内距离平方和最小,即
min S 1 , S 2 , ⋯ , S k ∑ i = 1 k ∑ a ∈ S i ∣ ∣ a − c i ∣ ∣ 2 s . t . { a 1 , a 2 , ⋯ , a n } = S 1 ∪ S 2 ∪ ⋯ ∪ S k S j ∩ S j ≠ ∅ , ∀ i ≠ j (3.10.2) \min_{S_1,S_2,\cdots,S_k}\sum_{i=1}^k\sum_{a{\in}S_i}||a-c_i||^2 \\ s.t. {\quad} \{a_1,a_2,\cdots,a_n\}=S_1\cup{S_2}\cup{\cdots}\cup{S_k} \\ S_j \cap S_j {\not=}\varnothing,\forall{i {\not=}j} \tag{3.10.2} S1,S2,⋯,Skmini=1∑ka∈Si∑∣∣a−ci∣∣2s.t.{a1,a2,⋯,an}=S1∪S2∪⋯∪SkSj∩Sj=∅,∀i=j(3.10.2)
问题(3.10.2)的自变量是数据点集合的分割方式,看起来比较难以处理,因此有必要将问题写成我们熟悉的形式,接下来给出问题的两种矩阵表达方式,它们之间是等价的。
1. K-均值聚类等价表述一
在原始聚类问题中,组内距离平方和定义为(3.10.1),即需要计算 S i S_i Si中的点到它们中心点 c i c_i ci的平方和,实际上,选取中心点 c i c_i ci作为参考点并不是必须的,我们完全可以选取其他点 h i h_i hi来作为参照来计算组内距离(其实这个 h i h_i hi通过优化最后也是表示的中心点),因此组内距离平方和可以推广为
W ( S 1 , S 2 , ⋯ , S k , H ) = ∑ i = 1 k ∑ a ∈ S i ∣ ∣ a − h i ∣ ∣ 2 W(S_1,S_2,\cdots,S_k,H)=\sum_{i=1}^k\sum_{a{\in}S_i}||a-h_i||^2 W(S1,S2,⋯,Sk,H)=i=1∑ka∈Si∑∣∣a−hi∣∣2
其中 H ∈ R k × p H{\in}R^{k \times p} H∈Rk×p(k个类的一个点(维度为p))且第 i i i行的向量为 h i T h_i^T hiT,为了表示聚类方式 S 1 , S 2 , ⋯ , S k S_1,S_2,\cdots,S_k S1,S2,⋯,Sk,一个很自然的想法是使用一个向量 ϕ i ∈ R k {\phi_i}{\in}R^k ϕi∈Rk来表示 a i a_i ai所处的类别
( ϕ i ) j = { 1 , a i ∈ S j 0 , a i ∉ S j {(\phi_i)}_j=\left\{ \begin{matrix} 1,a_i{\in}S_j \\ 0,a_i{\notin}S_j \end{matrix} \right. (ϕi)j={1,ai∈Sj0,ai∈/Sj
聚类问题等价描述为
min ϕ , H ∣ ∣ A − Φ H ∣ ∣ F 2 s . t . Φ ∈ R n × k ,每一行只有一个元素为 1 ,其余为 0 H ∈ R k × p (3.10.3) \min_{\phi,H}||A-{\Phi}H||_F^2 \\ s.t. {\quad}{\Phi}{\in}R^{n \times k},每一行只有一个元素为1,其余为0 \\ H{\in}R^{k \times p}\tag{3.10.3} ϕ,Hmin∣∣A−ΦH∣∣F2s.t.Φ∈Rn×k,每一行只有一个元素为1,其余为0H∈Rk×p(3.10.3)
这里的 Φ {\Phi} Φ的第 i i i行的向量就是 ϕ i T {\phi}_i^T ϕiT
接下来说明3.10.3和原问题3.10.2是等价的,为此只需要说明参考点集 H H H的取法实际上就是每一类的中点,当固定 P h i Phi Phi时,第 i i i类点的组内距离平方和为
∑ a ∈ S i ∣ ∣ a − h i ∣ ∣ 2 \sum_{a{\in}S_i}||a-h_i||^2 a∈Si∑∣∣a−hi∣∣2
根据二次函数的性质,当 h i = 1 n ∑ a ∈ S i a h_i=\frac{1}{n}{\sum_{a{\in}S_i}}a hi=n1∑a∈Sia时,组内距离平方和最小
所以 h i h_i hi一定会被优化成第 i i i类的中心点的
我们引入问题(3.10.3)的理由有两个
(1)形式简洁,且将不易处理的自变量“分割方式”转化为矩阵
(2)可以看成是一个矩阵分解问题,便于我们设计算法
2.K-均值聚类等价表述二
K-均值聚类的第二种等价表述利用了列正交矩阵的性质,这种表达方式比问题(3.10.3)相比更为简洁,首先定义 I S t , 1 ≤ t ≤ k I_{S_t},1{\le}t{\le}k ISt,1≤t≤k为 n n n维空间中每个分量取值0或1的向量,且
I S j ( i ) = { 1 , a i ∈ S t 0 , a i ∉ S t I_{S_j}(i)=\left\{ \begin{matrix} 1,a_i{\in}S_t \\ 0,a_i{\notin}S_t \end{matrix} \right. ISj(i)={1,ai∈St0,ai∈/St
可以证明,第 t t t类 S t S_t St中每个点到其中心点的距离平方和可以写成 1 2 n t T r ( D I S t I S t T ) \frac{1}{2n_t}Tr(DI_{S_t}I_{S_t}^T) 2nt1Tr(DIStIStT),其中 D ∈ R n × n D{\in}R^{n \times n} D∈Rn×n的元素为 D i j = ∣ ∣ a i − a j ∣ ∣ 2 D_{ij}=||a_i-a_j||^2 Dij=∣∣ai−aj∣∣2。这说明 S t S_t St中每个点到中心点的距离平方和与 S t S_t St中所有点两两之间距离平方和有关,因此,我们将问题(3.10.2)转化为
min S 1 , S 2 , ⋯ , S k 1 2 T r ( D X ) s . t . X = ∑ t = 1 k 1 n t I S t I S t T S 1 ∪ S 2 ∪ ⋯ ∪ S k = { a 1 , a 2 , ⋯ , a n } S i ∩ S j = ∅ , ∀ i ≠ j (3.10.4) \min_{S_1,S_2,\cdots,S_k}\frac{1}{2}Tr(DX) \\ s.t. {\quad}X={\sum}_{t=1}^k\frac{1}{n_t}I_{S_t}I_{S_t}^T \\ S_1{\cup}S_2{\cup}\cdots{\cup}S_k=\{a_1,a_2,\cdots,a_n\} \\ S_i{\cap}S_j={\varnothing},\forall{i{\not=}j}\tag{3.10.4} S1,S2,⋯,Skmin21Tr(DX)s.t.X=∑t=1knt1IStIStTS1∪S2∪⋯∪Sk={a1,a2,⋯,an}Si∩Sj=∅,∀i=j(3.10.4)
对半正定举证 X X X进行分解 X = Y Y T , Y ∈ R n × k X=YY^T,Y{\in}R^{n \times k} X=YYT,Y∈Rn×k,我们可以进一步得到如下矩阵优化问题(这里 I I I是 n n n维向量且分量全为1)
min Y ∈ R n × k T r ( Y T D Y ) s . t . Y Y T I = I , Y Y T = I k , Y ≥ 0 (3.10.5) \min_{Y{\in}R^{n \times k}}Tr(Y^TDY) \\ s.t.{\quad}YY^TI=I, \\ YY^T=I_k,Y{\ge}0\tag{3.10.5} Y∈Rn×kminTr(YTDY)s.t.YYTI=I,YYT=Ik,Y≥0(3.10.5)
求得3.10.5的解 Y Y T YY^T YYT就对应(3.10.4)的解(说实话这一块我没看懂,Kmeans直接去做的话还是蛮简单的)
相关文章:
)
最优化:建模、算法与理论(优化建模——2)
3.10 K-均值聚类 聚类分析是 统计学中的一个基本问题,其在机器学习,数据挖掘,模式识别和图像分析中有着重要应用。聚类不同于分类,在聚类问题中我们仅仅知道数据点本身,而不知道每个数据点具体的标签。聚类分析的任务…...

库的相关操作
目录 一、创建数据库 1,创建数据库规则 2、创建案例 二、字符集和校验规则 1、查看系统默认字符集以及校验规则 2、查看数据库支持的字符集以及校验规则 3、校验规则对数据库的影响 三、操纵数据库 1、查看数据库和目前所在数据库 2、显示创建语句 3、修改数据库 4、…...

程序分区:全局区、常量区、栈区、堆区、代码区
#include <iostream> using namespace std; //全局变量 int g_a 10; int g_b 10; //全局常量 const int c_g_a 10; const int c_g_b 10;int main() { //局部变量 int a 10; int b 10; //打印地址 cout << "局部变量a地址为: " <…...

Jtti:windows虚拟机如何设定永久静态路由
在Windows虚拟机上设置永久静态路由需要使用命令行工具,具体步骤如下: 打开命令提示符: 在Windows虚拟机中,按下Win R组合键,输入"cmd"并按回车键,以打开命令提示符。 查看当前路由表࿱…...
之事务消息)
RocketMQ(3)之事务消息
一、发送事务消息案例 事务消息共有三种状态,提交状态、回滚状态、中间状态: TransactionStatus.CommitTransaction: 提交事务,它允许消费者消费此消息。TransactionStatus.RollbackTransaction: 回滚事务,它代表该消息将被删除…...
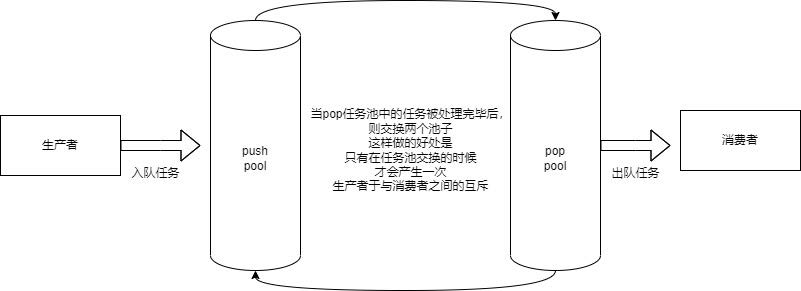
基于多设计模式下的同步异步日志系统
基于多设计模式下的同步&异步日志系统 代码链接:https://github.com/Janonez/Log_System 1. 项目介绍 本项目主要实现一个日志系统, 其主要支持以下功能: 支持多级别日志消息支持同步日志和异步日志支持可靠写入日志到标准输出、文件…...
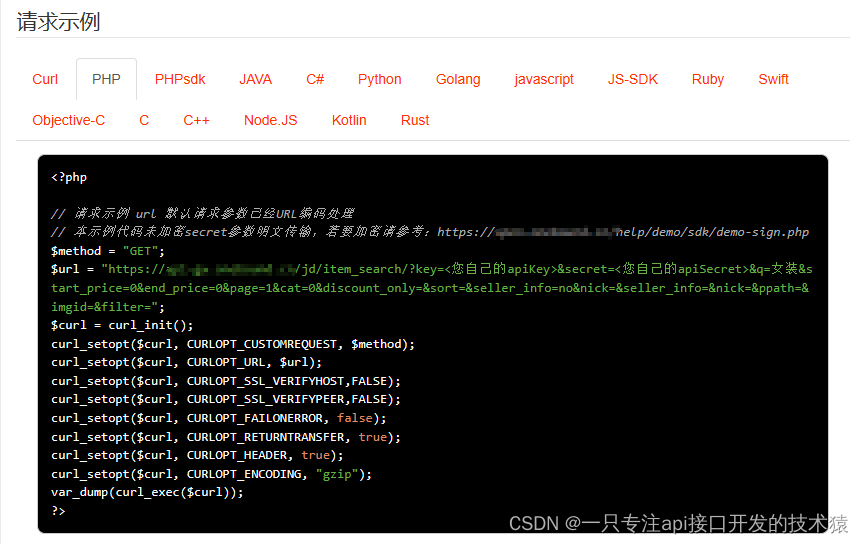
API接口与电商平台之间的联系,采集京东平台数据按关键字搜索商品接口示例
关键字搜索商品的重要性: 1.引入精准流量 关键词第一个也是最重要的作用就是为我们宝贝引进精准的流量,这一作用无论是在自然搜索中还是直通车中都是一样的。 第一步关乎的是我们宝贝的展现,而第二步用户是否会点进我们的宝贝,…...

代码随想录day41|343. 整数拆分96. 不同的二叉搜索树
343. 整数拆分 class Solution:def integerBreak(self, n: int) -> int:dp [0] *(n1)dp[2]1if n <3:return dp[n]for i in range(3,n1):for j in range(1,n):dp[i]max(j*(i-j),j*dp[i-j],dp[i])return dp[n] 96. 不同的二叉搜索树 class Solution:def numTrees(self, …...

Less常用内置函数
1,类型函数 isnumber(value) - 判断是否为数字isstring(value) - 判断是否为字符串isurl(value) - 判断是否为urliscolor(value) - 判断是否为颜色isunit(value, unit) - 判断value值是否为指定单位 示例: isnumber(12); // true isnumber(#333); // f…...
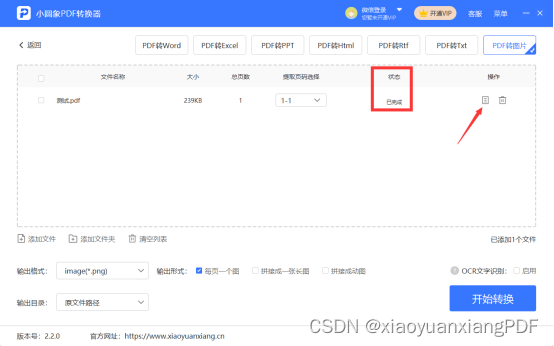
pdf转换成图片转换器在线怎么转?pdf转换成图片具体方法介绍
很多用户们都是比较喜欢使用pdf文档的,由于这种文件格式的便携性非常高,所以广泛的应用于工作和学习领域,再加上pdf文档可以随意转换成为其他的文件格式,更是让pdf文档受到了更多用户们的欢迎,那么pdf转换成图片转换器…...

JavaScript动态设置浏览器可视区域元素的文字颜色、监听滚动条、querySelectorAll、getBoundingClientRect
文章目录 前言htmlJavaScriptquerySelectorAllgetBoundingClientRect 前言 当元素出现在浏览器可视区域时给元素设置颜色等其他操作,比如当元素进入浏览器可视区域时,设置元素进入动画。 html <div id"idBox" class"box"><…...
意向客户的信息获取到底是怎样的,快来get一下
客户信息获取技术真的可以为企业提供精准客源吗?这个渠道到底安不安全,技术到底成不成熟?效果到底如何?下面简单的和大家分析一下。 客户信息获取技术是怎样的 手机采集引流方面,上量不精准,精准不上量的说…...

自动化测试常用脚本语言有哪些?
在自动化测试中,常用的脚本语言包括: 1. Python:Python是一个简洁、易读且功能强大的脚本语言,广泛应用于自动化测试领域。它具有丰富的测试框架和库,可以用于Web、移动应用和API等各种类型的测试。 2. Java࿱…...

mapreduce 的工作原理以及 hdfs 上传文件的流程
推荐两篇博文 mapreduce 的工作原理: 图文详解 MapReduce 工作流程_mapreduce工作流程_Shockang的博客-CSDN博客 hdfs 上传文件的流程 HDFS原理 - 知乎...

Ubuntu22.04安装ROS2
Ubuntu22.04安装ROS2 Excerpt ROS2官方文档 ROS2清华镜像站sudo apt update sudo apt upgrade locale # check for UTF-8 sudo apt update && sudo apt install locales sudo locale-gen en_US en_US.UTF-8 sudo update-locale LC_ALLe… ROS2官方文档 ROS2清华镜像站…...
uniapp - 倒计时组件-优化循环时间倒计时
使用定时器的规避方法 为了避免定时器误差导致倒计时计算错误,可以采用一些规避方法,比如将倒计时被中断时的剩余时间记录下来,重新开启定时器时再将这个剩余时间加到新的计算中。同时,为了避免定时器延迟,可以在每次执…...

java 实现访问者模式
访问者模式是一种行为设计模式,它允许您在不修改对象结构的情况下,向对象结构中的元素添加新的操作。这通常用于解决对象结构中元素类型多变,但操作类型相对稳定的问题。在访问者模式中,我们有一个访问者接口和多个具体的元素类&a…...

JDK源码剖析之PriorityQueue优先级队列
写在前面 版本信息: JDK1.8 PriorityQueue介绍 在数据结构中,队列分为FIFO、LIFO 两种模型,分别为先进先出,后进后出、先进后出,后进先出(栈) 而一切数据结构都是基于数组或者是链表实现。 在…...

TSINGSEE青犀AI视频分析/边缘计算/AI算法·人脸识别功能——多场景高效运用
旭帆科技AI智能分析网关可提供海量算法供应,涵盖目标监测、分析、抓拍、动作分析、AI识别等,可应用于各行各业的视觉场景中。同时针对小众化场景可快速定制AI算法,主动适配大厂近百款芯片,打通云/边/端灵活部署,算法一…...
算法_C++——最大连续 1 的个数 III)
力扣(LeetCode)算法_C++——最大连续 1 的个数 III
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 示例 1: 输入:nums [1,1,1,0,0,0,1,1,1,1,0], K 2 输出:6 解释:[1,1,1,0,0,1,1,1,1,1,1] 粗体数字…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
