【Luogu】 P5445 [APIO2019] 路灯
题目链接
点击打开链接
题目解法
转化很妙
考虑关路灯 x x x 的操作
令左边第一个未关的路灯为 L L L,右边第一个未关的路灯为 R R R,那么这一次会影响的区间即为 l ∈ [ L + 1 , x ] , r ∈ [ x , R − 1 ] l\in[L+1,x],\;r\in[x,R-1] l∈[L+1,x],r∈[x,R−1],既然有 2 个限制,那么我们把限制变成二维平面上的矩阵,即把左上为 ( L + 1 , x ) (L+1,x) (L+1,x),右下为 ( x , R − 1 ) (x,R-1) (x,R−1) 的矩阵变为 0
开路灯的操作类似
考虑询问的是什么?
即 1 1 1 到 q − 1 q-1 q−1 次每个版本 ( x , y ) (x,y) (x,y) 位置的和
考虑给矩阵定义一个增加(或减少)值,使查询变成只要查询第 i i i 个版本的 ( x , y ) (x,y) (x,y) 值
这里直接给出:对于第 i i i 个操作,加上或减去值为 i − q i-q i−q
考虑先开路灯,再关路灯的操作,即为 T − i − ( T − j ) = j − i T-i-(T-j)=j-i T−i−(T−j)=j−i,恰好为答案,这可以拓展到多个开关路灯的操作
这里需要一个特判,如果查询第 i i i 个版本从 x x x 可以到 y y y,那么答案需要 − ( q − i ) -(q-i) −(q−i)
可以把矩形变成 4 个区域的加减,然后不难发现,这就是一个三维偏序,可以考虑离线 c d q cdq cdq
时间复杂度 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
#include <bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;
const int N=300100;
struct Node{ int x1,x2,v,op,id;}q[N*10],t[N*10];
int idx,n,m,state[N],ans[N],tr[N];
char str[N];
set<int> se;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void ADD(int x,int y,int v){ q[++idx]={x,y,v,0,0};}
void add_square(int x1,int x2,int y1,int y2,int v){ADD(x2,y2,v);if(x1>1) ADD(x1-1,y2,-v);if(y1>1) ADD(x2,y1-1,-v);if(x1>1&&y1>1) ADD(x1-1,y1-1,v);
}
void work(int x,int t){if(!state[x]){auto it=se.upper_bound(x);int R=*it,L=*(--it);se.insert(x);add_square(L+1,x,x,R-1,-(m-t));}else{se.erase(x);auto it=se.upper_bound(x);int R=*it,L=*(--it);add_square(L+1,x,x,R-1,m-t);}
}
void add(int x,int y){ for(;x<=n;x+=lowbit(x)) tr[x]+=y;}
int ask(int x){if(!x) return 0;int res=0;for(;x;x-=lowbit(x)) res+=tr[x];return res;
}
void cdq(int l,int r){if(l==r) return;int mid=(l+r)>>1;cdq(l,mid),cdq(mid+1,r);int i=l,j=mid+1,k=0;while(i<=mid||j<=r){if(j>r||(i<=mid&&q[i].x1>=q[j].x1)){if(!q[i].op) add(q[i].x2,q[i].v);t[++k]=q[i],i++;}else{if(q[j].op) ans[q[j].id]+=ask(n)-ask(q[j].x2-1);t[++k]=q[j],j++;}}for(i=l;i<=mid;i++) if(!q[i].op) add(q[i].x2,-q[i].v);for(int i=1,j=l;i<=k;i++,j++) q[j]=t[i];
}
bool con(int x,int y){ return ask(y)-ask(x-1)==y-x+1;}
int main(){n=read(),m=read();scanf("%s",str+1);for(int i=1;i<=n;i++) state[i]=str[i]-48;add_square(1,n,1,n,m);se.insert(0),se.insert(n+1);for(int i=1;i<=n;i++) if(state[i]) add(i,1);for(int i=1;i<=n;i++) if(!state[i]) work(i,0);for(int i=1;i<=m;i++){char op[10];scanf("%s",op);if(op[0]=='t'){int x=read();state[x]^=1,work(x,i);ans[i]=-1e9;if(state[x]) add(x,1);else add(x,-1);}else{int x=read(),y=read();y--;if(con(x,y)) ans[i]=-(m-i);q[++idx]={x,y,0,1,i};}}memset(tr,0,sizeof(tr));cdq(1,idx);for(int i=1;i<=m;i++) if(ans[i]!=-1e9) printf("%d\n",ans[i]);return 0;
}相关文章:

【Luogu】 P5445 [APIO2019] 路灯
题目链接 点击打开链接 题目解法 转化很妙 考虑关路灯 x x x 的操作 令左边第一个未关的路灯为 L L L,右边第一个未关的路灯为 R R R,那么这一次会影响的区间即为 l ∈ [ L 1 , x ] , r ∈ [ x , R − 1 ] l\in[L1,x],\;r\in[x,R-1] l∈[L1,x],…...
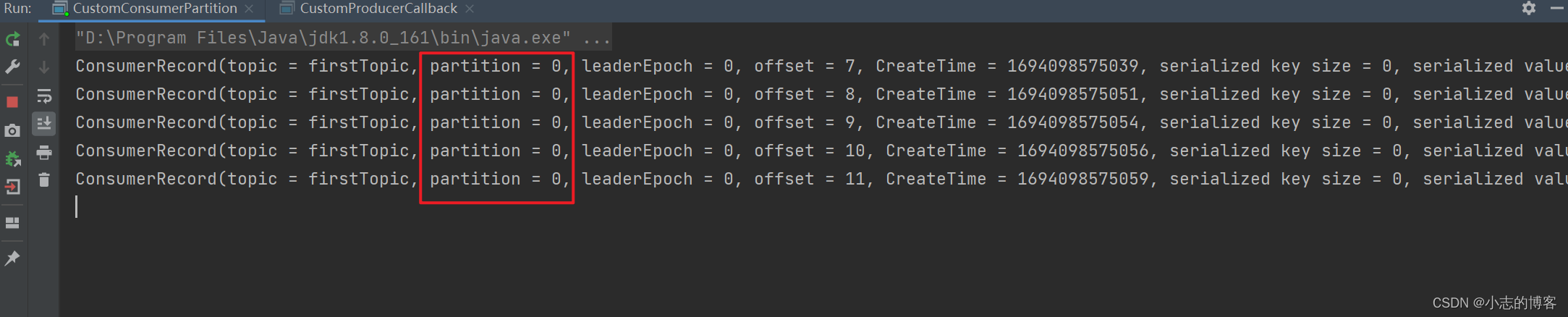
Kafka3.0.0版本——消费者(独立消费者消费某一个主题中某个分区数据案例__订阅分区)
目录 一、独立消费者消费某一个主题中某个分区数据案例1.1、案例需求1.2、案例代码1.3、测试 一、独立消费者消费某一个主题中某个分区数据案例 1.1、案例需求 创建一个独立消费者,消费firstTopic主题 0 号分区的数据,所下图所示: 1.2、案…...
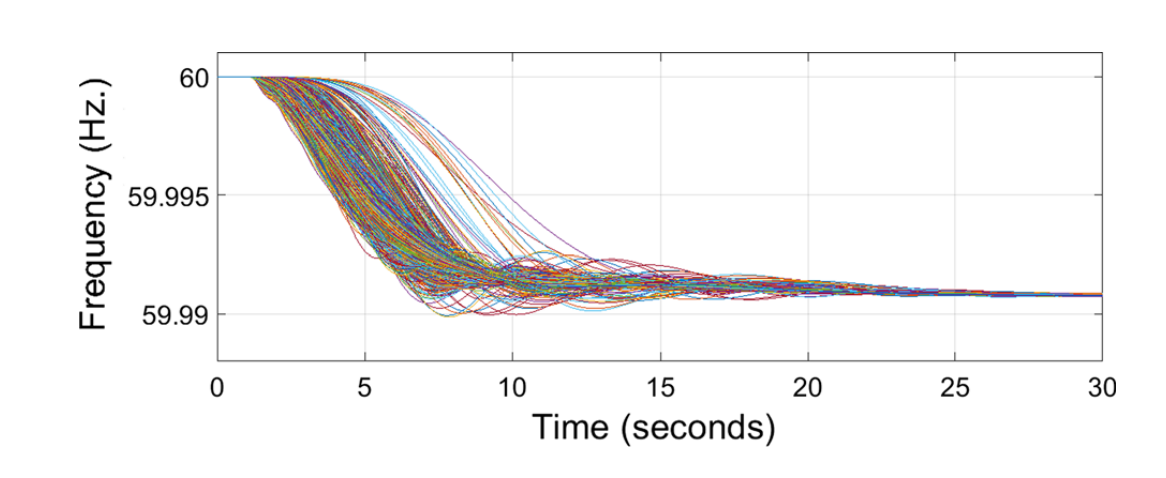
基于Simulink的用于电力系统动态分析
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

日200亿次调用,喜马拉雅网关的架构设计
说在前面 在40岁老架构师 尼恩的读者社区(50)中,很多小伙伴拿到一线互联网企业如阿里、网易、有赞、希音、百度、滴滴的面试资格。 最近,尼恩指导一个小伙伴简历,写了一个《API网关项目》,此项目帮这个小伙拿到 字节/阿里/微博/…...

构造函数和析构函数(个人学习笔记黑马学习)
构造函数:主要作用在于创建对象时为对象的成员属性赋值,构造函数由编译器自动调用,无须手动调用。析构函数:主要作用在于对象销毁前系统自动调用,执行一些清理工作。 #include <iostream> using namespace std;//对象初始化和清理class…...
GPT引领前沿与应用突破之GPT4科研实践技术与AI绘图教程
详情点击链接:GPT引领前沿与应用突破之GPT4科研实践技术与AI绘图教程 前沿 GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。 如在科研编程、绘图领域: 1、编程建议和示例代码: 无论你使用的编程语言是…...

Git上传新项目
第一步:初始化 Git 仓库 首先,打开终端或命令行界面,然后导航到项目目录。运行下面的命令来初始化一个新的 Git 仓库: git init这将创建一个新的 .git 子目录,其中包含了初始化的 Git 仓库。 第二步:添加…...

C语言文件操作总结
目录 字符方式读入文件 数据块方式读写文件 文件定位与随机读写 文件中数据的修改 字符方式读入文件 1.向文件中写入(输入字符) 用 fputc 函数或 puts 函数可以把一个字符写到磁盘文件中去。 int fputc(int ch,FILE * fp) ch 是要输出的字符&#…...
)
原生js之dom如何进行事件监听(事件捕获/冒泡)
那么好,这次主要讲解的就是dom是如何进行事件监听和事件取消监听的,我们知道vue中主要用watch来进行监听. js监听与取消监听 那么原生js主要用到的就是addListenEvent事件来进行监听,可以监听文档dom对象也可以监听浏览器bom对象,监听事件的语法结构如下 Dom/Bom监听 eleme…...
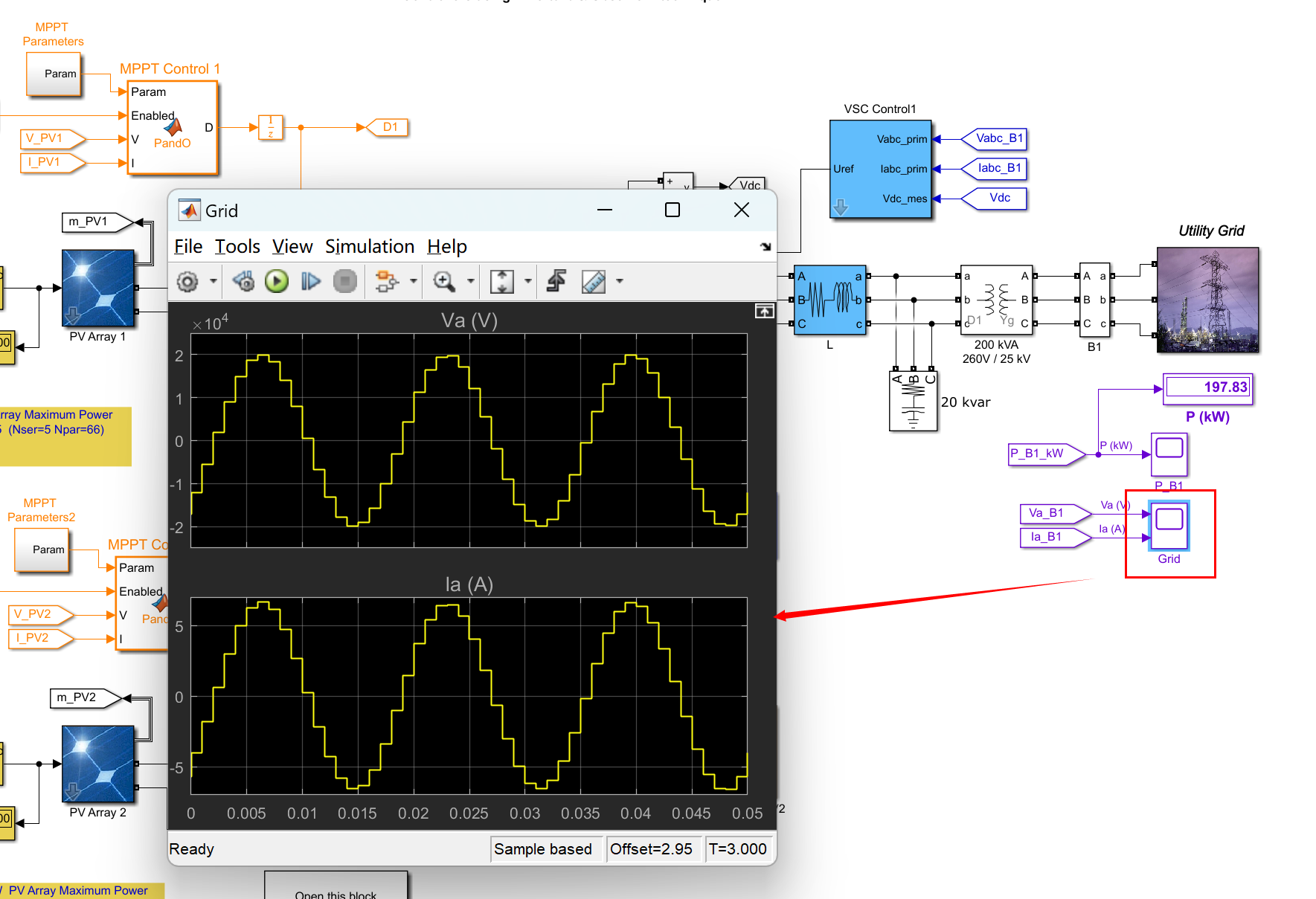
使用SimPowerSystems并网光伏阵列研究(Simulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

BUUCTF-WEB-[ACTF2020 新生赛]Includel
打开靶机 点击tips 利用Burp抓包,未见异常 但发现了响应头是 PHP/7.3.13 想到了"php://input"伪协议POST发送PHP代码 构建Payload:?filephp://filter/readconvert.base64-encode/resourceflag.php 这里需要注意的是使用php://filter伪协议…...

算法通关村十四关:白银挑战-堆能高效解决的经典问题
白银挑战-堆能高效解决的经典问题 1.在数组中找第K大的元素 LeetCode215 https://leetcode.cn/problems/kth-largest-element-in-an-array/ 思路分析 主要解决方法有3个,选择法,堆查找法和快速排序法 方法1:选择法 先遍历一遍找到最大的…...

跨站请求伪造(CSRF)攻击与防御原理
跨站请求伪造(CSRF) 1.1 CSRF原理 1.1.1 基本概念 跨站请求伪造(Cross Site Request Forgery,CSRF)是一种攻击,它强制浏览器客户端用户在当前对其进行身份验证后的Web 应用程序上执行非本意操作的攻击&a…...

从0到1实现播放控制器
这系列文章主要讲诉如何从0到1使用QT实现带时间显示、滚动字幕等的自定义配置视频播放控制器。平时我们乘坐地铁经常看到各条线的播放控制器都大同小异。其实都是通过QT等界面开发软件来实现的。 在具体开发之前,需要明确我们需要做什么? 1. 开发一个可…...

【Vue-Element-Admin】导出el-table全部数据
背景 因为el-table实现了分页查询,所以想要实现el-table需要重新编写一个查询全部数据的方法 查询全部数据 listQuery: export default{return{listQuery:{//page:1,//limit:20,//如果想兼容按条件导出,可以定义查询条件age:undefined,sex:undefined…...

MFC 更改控件的大小和位置
获取当前主窗体的位置rect CRect dlgNow;GetWindowRect(&dlgNow);获取某一个控件当前的位置 CRect rect;CButton* pBtn (CButton*)GetDlgItem(IDC_BUTTONXXX);//获取按钮控件pBtn->GetWindowRect(rect);CWnd* pWnd(CWnd*)GetDlgItem(IDC_EDITXXX);//其它控件࿰…...
)
【向量数据库】相似向量检索Faiss数据库的安装及余弦相似度计算(C++)
目录 简介安装方法安装OpenBLAS安装lapack编译Faiss 代码示例余弦相似度计算输出ID号而非索引的改进版 简介 Faiss 是一个强大的向量相似度搜索库,具有以下优点: 高效的搜索性能:Faiss 在处理大规模向量数据时表现出色。它利用了高度优化的索…...
教育培训小程序的设计与功能解析
随着互联网的发展,线上教育逐渐成为一种趋势,越来越多的人开始选择在线学习。而搭建一个适合自己的线上教育小程序,可以为教育机构或个人提供更好的教学和学习体验。在本文中,我们将介绍如何通过一个第三方制作平台来搭建在线教育…...
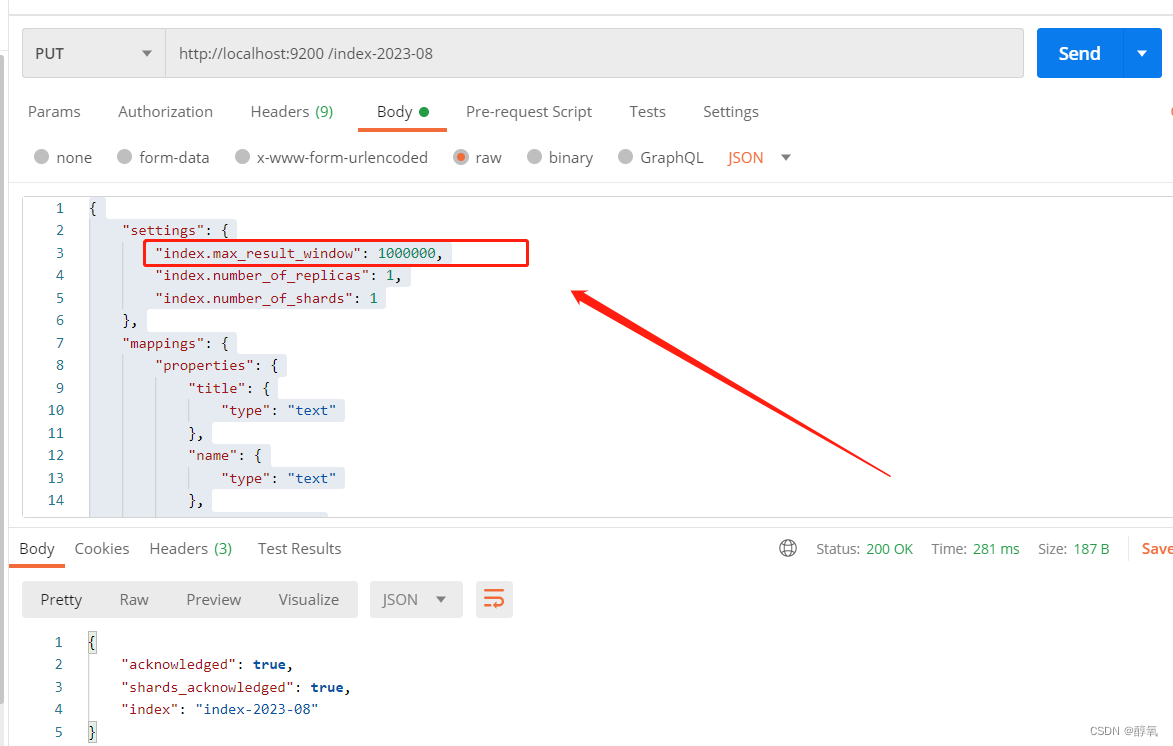
【ES】illegal_argument_exception“,“reason“:“Result window is too large
查询ES数据返回错误: {"root_cause":[{"type":"illegal_argument_exception","reason":"Result window is too large, from size must be less than or equal to: [10000] but was [999999]. See the scroll api for…...

SpringBoot实现登录拦截
如果我们不进行登录拦截的话,即使我们跳过登录页面直接去访问任意一个页面也能访问成功,那么登录功能就没有意义,同时也会存在安全问题,因为有些操作是要用户登录后才能执行的,如果用户没有登录,该接口就获…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

SFTrack:面向警务无人机的自适应多目标跟踪算法——突破小尺度高速运动目标的追踪瓶颈
【导读】 本文针对无人机(UAV)视频中目标尺寸小、运动快导致的多目标跟踪难题,提出一种更简单高效的方法。核心创新在于从低置信度检测启动跟踪(贴合无人机场景特性),并改进传统外观匹配算法以关联此类检测…...

多模态大语言模型arxiv论文略读(110)
CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文标题:CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文作者:Hidehisa Arai, Keita Miwa, Kento Sasaki, Yu Yamaguchi, …...
