【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录
- 【`获取资源`请见文章第5节:资源获取】
- 1. 原始POA算法
- 2. 改进后的IPOA算法
- 2.1 随机对立学习种群初始化
- 2.2 动态权重系数
- 2.3 透镜成像折射方向学习
- 3. 部分代码展示
- 4. 仿真结果展示
- 5. 资源获取
【获取资源请见文章第5节:资源获取】
1. 原始POA算法
此算法详细介绍请参考POA算法介绍
2. 改进后的IPOA算法
2.1 随机对立学习种群初始化
采用随机方法初始化POA种群,生成的种群不均匀,影响了收敛速度和精度。为了获得更好的初始种群,本文采用了随机对立学习策略来进行种群初始:
X i , n e w = ( l + u ) − k X i (1) X_{i,new}=(l+u)-kX_{i}\tag1 Xi,new=(l+u)−kXi(1)
其中, X i X_{i} Xi为原解, X i , n e w X_{i,new} Xi,new为随机对立学习生成的反向解, k k k为[0,1]之间的随机数。
经过随机对立学习策略后,生成了 N N N个反向解,如果反向解的适应度值优于原解,就用反向解替代原解,否则保留原解。
2.2 动态权重系数
基本鹈鹕优化算法的开发阶段,在迭代后期会存在陷入局部最优的情况,使搜索失败。为克服这一弊端,再在其位置更新公式中加入动态权重系数 ω,让它在迭代初期具有较大值,促进全局搜索,迭代后期自适应变小,促进局部搜索并加快收敛速度。
2.3 透镜成像折射方向学习
透镜成像折射反向学习策略的思想来自于凸透镜成像的原理。通过基于当前坐标生成一个反向位置来扩展搜索范围,如图1所示。

在二维坐标中,x轴的搜索范围为(a, b), y轴表示一个凸透镜。假设物体A在x轴上的投影为x,高度为h,通过透镜成像,另一侧的图像为A*, A在x轴上的投影为x,高度为h*。通过以上分析,我们可以得到如下公式:
( a + b ) / 2 − x x ∗ − ( a + b ) / 2 = h h ∗ (2) \frac{(a+b)/2-x}{x^{*}-(a+b)/2 }=\frac{h}{h^{*}} \tag2 x∗−(a+b)/2(a+b)/2−x=h∗h(2)
对公式(2)进行转换,即可得到反向解x*的表达式为:
x ∗ = a + b 2 + a + b 2 k − x k (3) x^{*} =\frac{a+b}{2}+\frac{a+b}{2k}-\frac{x}{k} \tag3 x∗=2a+b+2ka+b−kx(3)
其中, k = h / h ∗ k=h/h^{*} k=h/h∗, a a a和 b b b可以视为某维度的上下限。本文中的 k k k是一个与迭代次数相关的动态自适应值。
3. 部分代码展示
%%
clc
clear
close all%%
Fun_name='F1'; % number of test functions: 'F1' to 'F23'
SearchAgents=30; % number of Pelicans (population members)
Max_iterations=500; % maximum number of iteration
[lb,ub,dim,fobj]=Get_Functions_details(Fun_name); % Object function information
[Best_score_POA,Best_pos_POA,POA_curve]=POA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_SSA,Best_pos_SSA,SSA_curve]=SSA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_WOA,Best_pos_WOA,WOA_curve]=WOA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_GWO,Best_pos_GWO,GWO_curve]=GWO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_IPOA,Best_pos_IPOA,IPOA_curve]=IPOA(SearchAgents,Max_iterations,lb,ub,dim,fobj);%%
figure('Position',[454 445 694 297]);
subplot(1,2,1);
func_plot(Fun_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])subplot(1,2,2);
t = 1:Max_iterations;
semilogy(t, POA_curve, 'b-', t, SSA_curve, 'k-', t, WOA_curve, 'g-', t, GWO_curve, 'm-', t, IPOA_curve, 'r-','linewidth', 1.5);title(Fun_name)
xlabel('Iteration');
ylabel('Best fitness function');
axis tight
legend('POA','SSA','WOA','GWO','IPOA')display(['The best solution obtained by POA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_POA)]);
display(['The best optimal value of the objective funciton found by POA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_POA)]);
display(['The best solution obtained by SSA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_SSA)]);
display(['The best optimal value of the objective funciton found by SSA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_SSA)]);
display(['The best solution obtained by WOA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_WOA)]);
display(['The best optimal value of the objective funciton found by WOA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_WOA)]);
display(['The best solution obtained by GWO for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_GWO)]);
display(['The best optimal value of the objective funciton found by GWO for ' [num2str(Fun_name)],' is : ', num2str(Best_score_GWO)]);
display(['The best solution obtained by IPOA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_IPOA)]);
display(['The best optimal value of the objective funciton found by IPOA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_IPOA)]);
4. 仿真结果展示









5. 资源获取
可以获取完整代码资源。
相关文章:

【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录 【获取资源请见文章第5节:资源获取】1. 原始POA算法2. 改进后的IPOA算法2.1 随机对立学习种群初始化2.2 动态权重系数2.3 透镜成像折射方向学习 3. 部分代码展示4. 仿真结果展示5. 资源获取 【获取资源请见文章第5节:资源获取】 1. 原始POA算法…...

k8s 入门到实战--部署应用到 k8s
k8s 入门到实战 01.png 本文提供视频版: 背景 最近这这段时间更新了一些 k8s 相关的博客和视频,也收到了一些反馈;大概分为这几类: 公司已经经历过服务化改造了,但还未接触过云原生。公司部分应用进行了云原生改造&…...

编程语言新特性:instanceof的改进
以前也写过类似的博文,可能重复。 要判断一个对象是哪个类或父类的实例,JAVA用到instanceof,其实语言也有类似语法。而类一般是多层继承的,有时就让人糊涂。所以我提出改进思路: instanceof:保持不变。ins…...
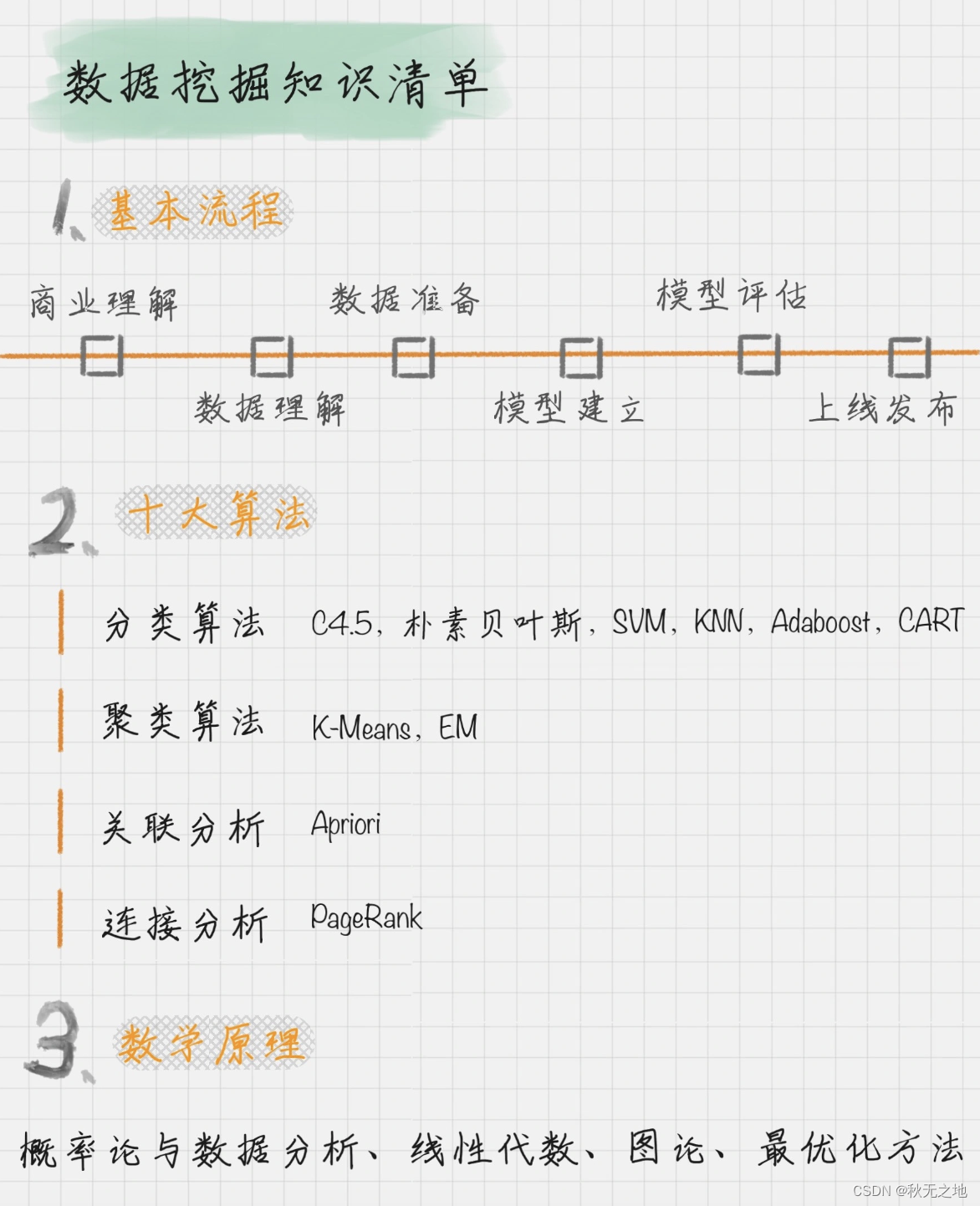
数据挖掘的学习路径
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...
逻辑回归Logistic
回归 概念 假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程。 最后结果用sigmoid函数输出 因此,为了实现 Logisti…...
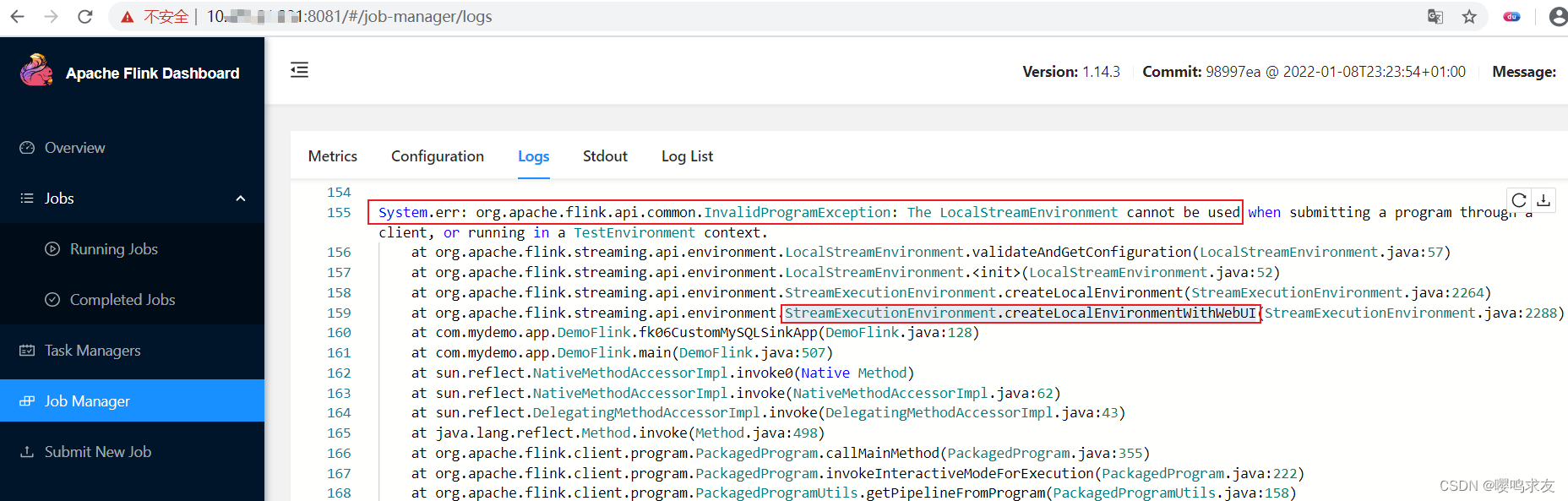
Flink提交jar出现错误RestHandlerException: No jobs included in application.
今天打包一个flink的maven工程为jar,通过flink webUI提交,发现居然报错。 如上图所示,提示错误为: Server Response Message: org.apache.flink.runtime.rest.handler.RestHandlerException: No jobs included in application. …...
】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处)
【数仓基础(一)】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处
文章目录 一. 数据仓库的概念1. 面向主题2. 集成3. 随时间变化4. 非易失粒度 二. 建立数据仓库的原因三. 使用数据仓库的好处 一. 数据仓库的概念 数据仓库的主要作用: 数据仓库概念主要是解决多重数据复制带来的高成本问题。 在没有数据仓库的时代,需…...
电商类面试问题--01Elasticsearch与Mysql数据同步问题
在实现基于关键字的搜索时,首先需要确保MySQL数据库和ES库中的数据是同步的。为了解决这个问题,可以考虑两层方案。 全量同步:全量同步是在服务初始化阶段将MySQL中的数据与ES库中的数据进行全量同步。可以在服务启动时,对ES库进…...
天线材质介绍--FPC天线
...

vue3 的 ref、 toRef 、 toRefs
1、ref: 对原始数据进行拷贝。当修改 ref 响应式数据的时候,模版中引用 ref 响应式数据的视图处会发生改变,但原始数据不会发生改变 <template><div>{{refA}}</div> </template><script lang"ts" setup> impor…...
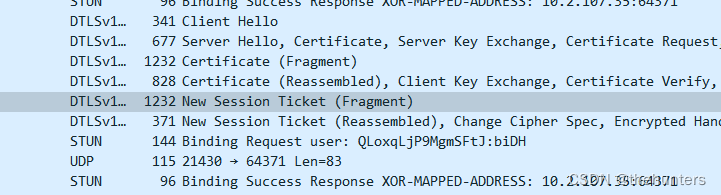
WebRTC中 setup:actpass、active、passive
1、先看一下整个DTLS的流程 setup:actpass、active、passive就发生在Offer sdp和Anser SDP中 Offer的SDP是setup:actpass,这个是服务方: v0\r o- 1478416022679383738 2 IN IP4 127.0.0.1\r s-\r t0 0\r agroup:BUNDLE 0 1\r aextmap-allow-mixed\r amsid-semanti…...

ModuleNotFoundError: No module named ‘lavis‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

双指针的问题解法以及常见的leetcode例题。
目录 介绍: 问题1:双指针 剑指offer57 和为S的两个数字。 问题2:剑指Offer 21. 调整数组顺序使奇数位于偶数前面 问题3:连续奇数子串(笔试遇到的真题) 问题4:滑动窗口的最大值 介绍&#…...

python容器模块Collections
Python附带一个模块,它包含许多容器数据类型,名字叫作collections defaultdict defaultdict与dict类型不同,你不需要检查key是否存在,所以我们能这样做: from collections import defaultdict colours ((Yasoob, Y…...
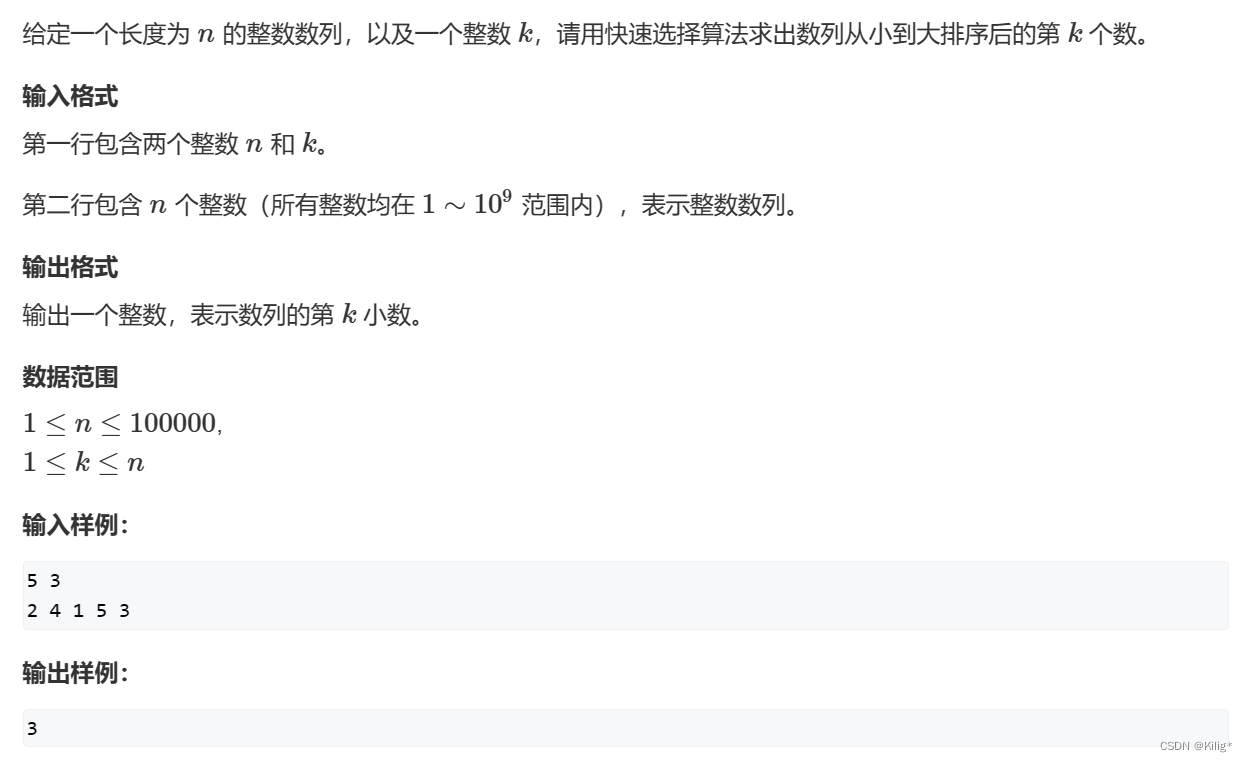
排序算法学习记录-快速排序
快速排序 快速排序关键在于确定一个中间值,使得小于这个中间值的数在左边,大于这个中间值的数在右边。那么中间值该如何确定呢?有以下几种做法 首元素,也就是arr[l]尾元素,也就是arr[r]中间元素,也就是ar…...

安装windows版本的ros2 humble的时候,最后报错
"[rti_connext_dds_cmake_module][warning] RTI Connext DDS environment script not found (\resource\scripts\rtisetenv_x64Win64VS2017.bat). RTI Connext DDS will not be available at runtime, unless you already configured PATH manually." 意思是没找到。…...

Nginx 学习(十)高可用中间件的配置与实现
一 Keepalived热备 1 概述 调度器出现单点故障,如何解决?Keepalived实现了高可用集群Keepalived最初是为LVS设计的,专门监控各服务器节点的状态Keepalived后来加入了VRRP功能,防止单点故障 2 运行原理 Keepalived检测每个服务器节点状…...

[刷题记录]牛客面试笔刷TOP101
牛客笔试算法必刷TOP101系列,每日更新中~ 1.合并有序链表2023.9.3 合并两个排序的链表_牛客题霸_牛客网 (nowcoder.com) 题意大致为: 将两个链表中的元素按照从小到大的顺序合并成为一个链表. 所给予的条件: 给出的所要合并的链表都是从小到大顺序排列的. 思路: 创建一…...

降水预报之双重惩罚
在降水预报中,通常会出现 "双重惩罚问题 "的指标或度量包括那些常用于预报验证的指标或度量。当假阴性(漏报降水事件)和假阳性(误报)受到同等惩罚或加权时,就会出现双重惩罚问题,这在…...
)
一条SQL语句的执行过程(附一次两段式提交)
一条SQL语句的完整执行过程是怎样的呢?我们用select和update语句来举例。 注意在mysql8后,进入服务层后,取消了去查询缓存(属于Server服务层)这个步骤,缓存中key是SQL语句,value是值,这样其实并不会提升性…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
