联合熵和条件熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
文章目录
- 联合熵
- 条件熵
联合熵
联合集 XY 上, 对联合自信息 I(xy)I(x y)I(xy) 的平均值称为联合熵:
H(XY)=Ep(xy)[I(x⇌y)]=−∑x∑yp(xy)logp(xy)\begin{array}{l} H(X Y)=\underset{p(x y)}{E}[I(x \rightleftharpoons y)] \\ =-\sum_{x} \sum_{y} p(x y) \log p(x y) \end{array} H(XY)=p(xy)E[I(x⇌y)]=−∑x∑yp(xy)logp(xy)
当有n个随机变量 X=(X1,X2,…,Xn)X=\left(X_{1}, X_{2}, \ldots, X_{n}\right)X=(X1,X2,…,Xn) , 有
H(X)=−∑X1,X2,…,Xnp(x1,x2,…,xn)logp(x1,x2,…,xn)H(\mathbf{X})=-\sum_{X_{1}, X_{2}, \ldots, X_{n}} p\left(x_{1}, x_{2}, \ldots, x_{n}\right) \log p\left(x_{1}, x_{2}, \ldots, x_{n}\right) H(X)=−X1,X2,…,Xn∑p(x1,x2,…,xn)logp(x1,x2,…,xn)
信息熵与热熵的关系
信息熵的概念是借助于热熵的概念而产生的。
-
信息熵与热熵含义相似
-
信息熵与热熵的区别:
- 信息熵的不增原理
- 热熵不减原理
-
热熵的减少等于信息熵的增加。
条件熵
联合集 XY\mathbf{X Y}XY 上, 条件自信息I(y/x)I(y / x)I(y/x)的平均值定义为条件熵:
H(Y/X)=Ep(xy)[I(y/x)]=−∑x∑yp(xy)logp(y/x)=∑xp(x)[−∑yp(y/x)logp(y/x)]=∑xp(x)H(Y/x)\begin{array}{l} H(Y / X)=\underset{p(x y)}{E}[I(y / x)]=-\sum_{x} \sum_{y} p(x y) \log p(y / x) \\ =\sum_{x} p(x)\left[-\sum_{y} p(y / x) \log p(y / x)\right]=\sum_{x} p(x) H(Y / x) \end{array} H(Y/X)=p(xy)E[I(y/x)]=−∑x∑yp(xy)logp(y/x)=∑xp(x)[−∑yp(y/x)logp(y/x)]=∑xp(x)H(Y/x)
推广:
H(Xn∣X1,…,Xn−1)=−∑X1,X2,…,Xnp(x1,x2,…,xn)logp(xn∣x1,…,xn−1)\begin{array}{l} H\left(X_{n} \mid X_{1}, \ldots, X_{n-1}\right) =-\sum_{X_{1}, X_{2}, \ldots, X_{n}} p\left(x_{1}, x_{2}, \ldots, x_{n}\right) \log p\left(x_{n} \mid x_{1}, \ldots, x_{n-1}\right) \end{array} H(Xn∣X1,…,Xn−1)=−∑X1,X2,…,Xnp(x1,x2,…,xn)logp(xn∣x1,…,xn−1)
注意:当有n个随机变量 X=(X1,X2,…,Xn)X=\left(X_{1}, X_{2}, \ldots, X_{n}\right)X=(X1,X2,…,Xn) 。
H(X,Y)=H(Y)+H(X∣Y)=H(X)+H(Y∣X)H(X)=H(X1)+H(X2∣X1)+…+H(Xn∣X1,X2,…,Xn−1)\begin{array}{l} H(X, Y)=H(Y)+H(X \mid Y)=H(X)+H(Y \mid X) \\ H(\mathbf{X}) =H\left(X_{1}\right)+H\left(X_{2} \mid X_{1}\right)+\ldots+H\left(X_{n} \mid X_{1}, X_{2}, \ldots, X_{n-1}\right) \end{array} H(X,Y)=H(Y)+H(X∣Y)=H(X)+H(Y∣X)H(X)=H(X1)+H(X2∣X1)+…+H(Xn∣X1,X2,…,Xn−1)
注意: H(X∣Y)\mathbf{H}(\mathbf{X} \mid \mathbf{Y})H(X∣Y) 表示已知变量 Y\mathbf{Y}Y 后, 对变量 X\mathbf{X}X 尚存在的平均不确定性(存在疑义)。
已知信源 X=[ABC1/31/31/3]X=\left[\begin{array}{ccc}A & B & C \\ 1 / 3 & 1 / 3 & 1 / 3\end{array}\right]X=[A1/3B1/3C1/3] 和 Y=[DEF1/103/53/10]Y=\left[\begin{array}{ccc}D & E & F \\ 1 / 10 & 3 / 5 & 3 / 10\end{array}\right]Y=[D1/10E3/5F3/10] ,请快速两个信源的信息熵的关系。
答:H(X) > H(Y)。其实不用计算,由上面可知一个简单的结论,等概率时信息熵最大。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
相关文章:

联合熵和条件熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录联合熵条件熵联合…...
)
华为OD机试真题Python实现【求最大数字】真题+解题思路+代码(20222023)
求最大数字 题目 给定一个由纯数字组成以字符串表示的数值,现要求字符串中的每个数字最多只能出现2次,超过的需要进行删除;删除某个重复的数字后,其它数字相对位置保持不变。 如34533,数字3重复超过2次,需要删除其中一个3,删除第一个3后获得最大数值4533 请返回经过删…...

Python爬虫(10)selenium爬虫后数据,存入csv、txt并将存入数据并对数据进行查询
之前的文章有关于更多操作方式详细解答,本篇基于前面的知识点进行操作,如果不了解可以先看之前的文章 Python爬虫(1)一次性搞定Selenium(新版)8种find_element元素定位方式 Python爬虫(2)-Selenium控制浏览…...
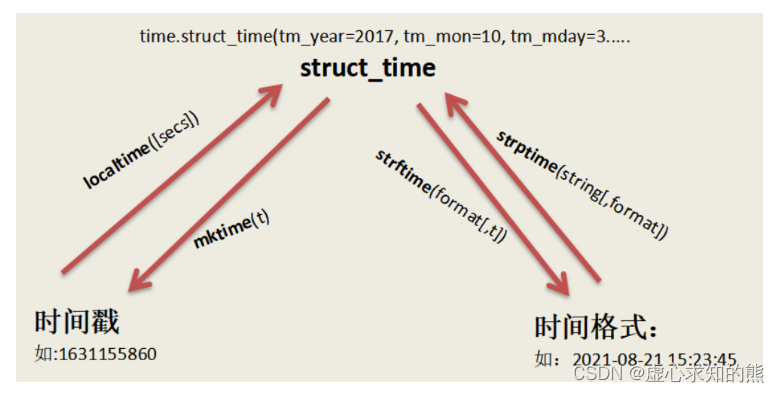
Python 之 Pandas 时间函数 time 、datetime 模块和时间处理基础
文章目录一、time 模块1、时间格式转换图2. struct_time 元组元素结构3. format time 结构化表示二、datetime 模块1. date类2. 方法和属性3. datetime 类三、timedelta 类的时间加减四、时间处理基础Python 中提供了对时间日期的多种多样的处理方式,主要是在 time …...

C语言学习及复习笔记-【5】C 运算符
文章目录5. C 运算符5.1 关系运算符5.2 逻辑运算符5.3 位运算符5.4 杂项运算符 ↦ sizeof & 三元5.5 例子1). 利用异或 ^ 来交换两个数的值,而且不引入其他变量。2). 利用位与 & 运算,判断一个整数是否是2的整数次幂。3). 不同长度的数据进行位运…...
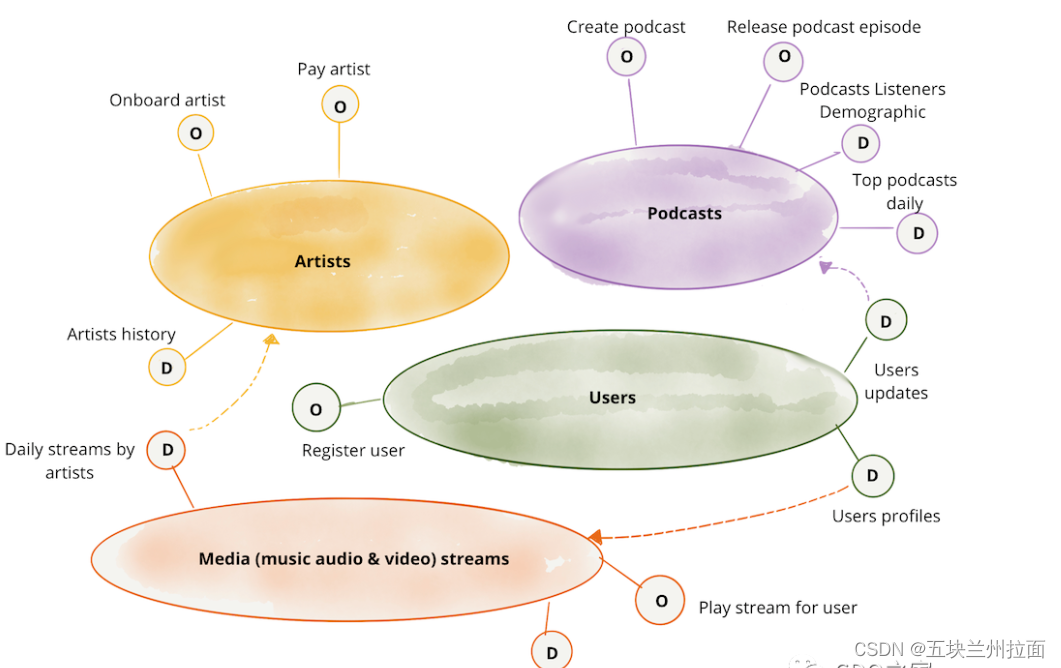
数仓、数据湖、湖仓一体、数据网格
第一代:数据仓库 定义 为解决数据库面对数据分析的不足,孕育出新一类产品数据仓库。数据仓库(Data Warehouse)是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持管理决策和信息的全局共享。 数…...

C语言【atoi函数】
C语言【atoi函数】🫅系统atoi函数🫅 模拟实现atoi函数看到atoi函数,有人又会问有这个函数,我怎么没用过。那就说明:不是你刷题太少,就是atoi函数存在感太低。 这篇函数就带你领略atoi函数的魅力 Ǻ…...

一起学习用Verilog在FPGA上实现CNN----(八)integrationFC设计
1 integrationFC设计 LeNet-5网络结构全连接部分如图所示,该部分有2个全连接层,1个TanH激活层,1个SoftMax激活层: 图片来自附带的技术文档《Hardware Documentation》 integrationFC部分原理图,如图所示,…...

面试题总结
1.js的数据类型 分为基本数据类型和引用数据类型。 基本数据类型 ES5的5种:Null,undefined,Boolean,Number,String, ES6新增:Symbol表示独一无二的值 ES10新增:BigInt 表示任意大的…...
go进阶(1) -深入理解goroutine并发运行机制
并发指的是同时进行多个任务的程序,Web处理请求,读写处理操作,I/O操作都可以充分利用并发增长处理速度,随着网络的普及,并发操作逐渐不可或缺 一、goroutine简述 在Golang中一个goroutines就是一个执行单元ÿ…...

mongodb 操作记录
#启动服务 net start MongoDB #停止服务 net stop MongoDB #进入mongo shell 方式 mongo db #查看当前数据库是那个 #插入一条数据 db.runoob.insert({x:10}) #查找数据 db.runoob.find() 查询所有的数据库 show dbs #连接mongodb mongodb://[username:password]host1[:po…...

JDBC简单的示例
JDBC 编程步骤 加载驱动程序: Class.forName(driverClass) //加载MySql驱动 Class.forName("com.mysql.jdbc.Driver") //加载Oracle驱动 Class.forName("oracle.jdbc.driver.OracleDriver")获得数据库连接: DriverManager.getCon…...
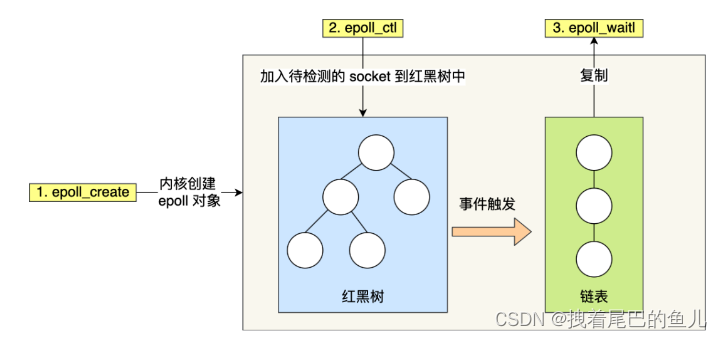
Spring架构篇--2.3 远程通信基础--IO多路复用select,poll,epoll模型
前言:对于传统的BIO(同步阻塞)模型,当有客户端连接达到服务端,服务端在对改连接进行连接建立,和数据传输过程中,是无法响应其他客户端的,只有当服务端完成对一个客户端处理后&#x…...
python--matplotlib(4)
前言 Matplotlib画图工具的官网地址是 http://matplotlib.org/ Python环境下实现Matlab制图功能的第三方库,需要numpy库的支持,支持用户方便设计出二维、三维数据的图形显示,制作的图形达到出版级的标准。 其他matplotlib文章 python--matpl…...
)
【项目精选】城市公交查询系统(论文+视频+源码)
点击下载源码 1.1 选题背景 随着低碳生活的普及,人们更倾向于低碳环保的出行方式,完善公交系统无疑具有重要意义。公交是居民日常生活中最常使用的交通工具之一,伴随着我国经济繁荣和城市人口增长,出行工具的选择也变得越来越重要…...
less、sass、webpack(前端工程化)
目录 一、Less 1.配置less环境 1.先要安装node:在cmd中:node -v检查是否安装node 2.安装less :cnpm install -g less 3.检查less是否安装成功:lessc -v 4.安装成功后,在工作区创建xx.less文件 5.在控制台编译less,命令&…...
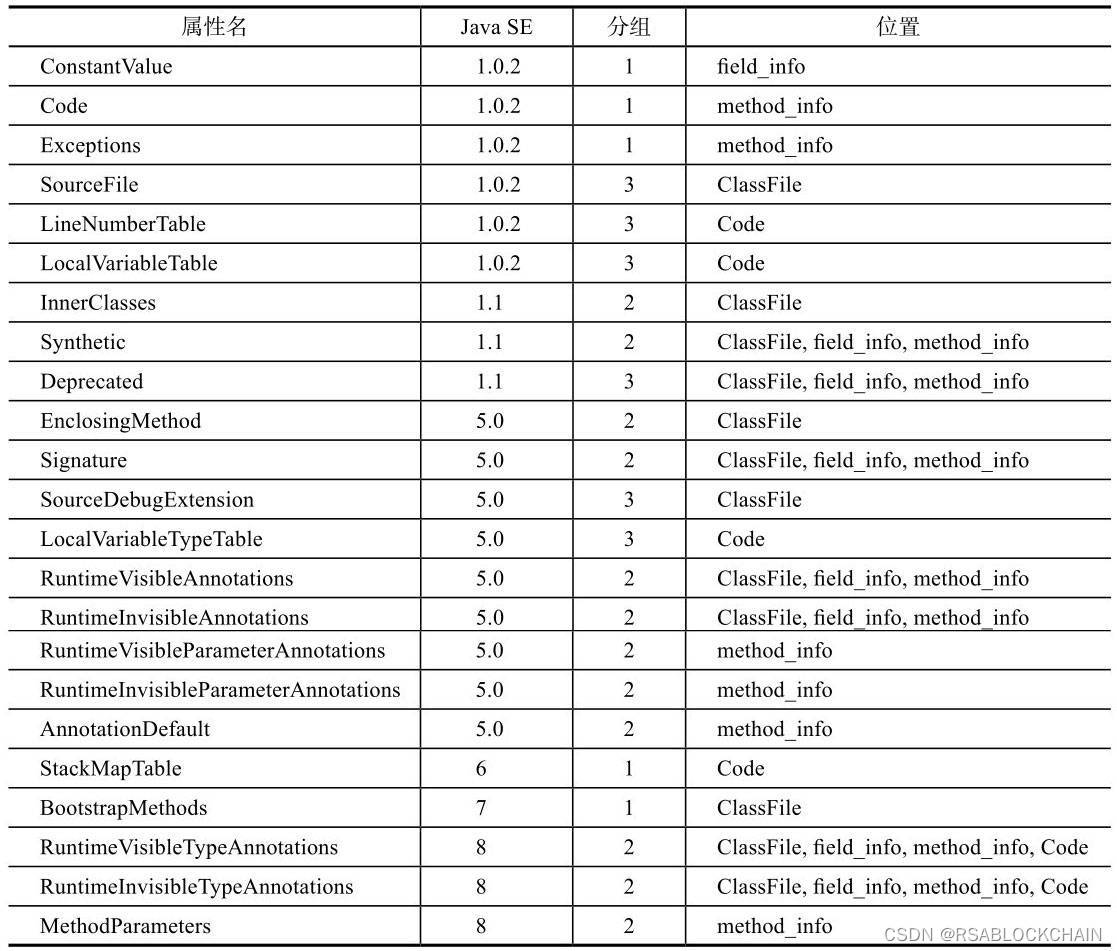
解析Java中的class文件
解析class文件需要把class文件当成文件流来处理,定义ClassReader结构体 type ClassReader struct {data []byte }go语言中的reslice语法可以跳过已经读过的数据。 同时定义了ClassFile数据结构来描述class文件的各个部分,该数据结构如下所示࿱…...

直播预告 | 企业如何轻松完成数据治理?火山引擎 DataLeap 给你一份实战攻略!
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 企业数字化转型正席卷全球,这不仅是趋势所在,也是企业发展必然面对的考题,也是企业最关心、最难决策的难题,数字化不…...
)
华为OD机试真题Python实现【 磁盘容量】真题+解题思路+代码(20222023)
磁盘容量 题目 磁盘的容量单位常用的有M、G、T 他们之间的换算关系为1T =1024G,1G=1024M 现在给定n块磁盘的容量,请对他们按从小到大的顺序进行稳定排序 例如给定5块盘的容量 5 1T 20M 3G 10G6T 3M12G9M 排序后的结果为 20M 3G 3M12G9M 1T 10G6T 注意单位可以重复出现 上述…...

php调试配置
错误信息输出 错误日志 nginx把对php的请求发给php-fpm fastcgi进程来处理,默认的php-fpm只会输出php-fpm的错误信息,在php-fpm的errors log里也看不到php的errorlog。原因是php-fpm的配置文件php-fpm.conf中默认是关闭worker进程的错误输出࿰…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
