算法比赛——必备的数论知识
秋名山码民的主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
🙏作者水平有限,如发现错误,还请私信或者评论区留言!
目录
- 一、欧几里得
- 二、扩展欧几里得
- 三、算术基本定理
- 四、线性筛选求质数
- 五、等差数列
- 六、等比数列
- 七、组合计数
- 最后
一、欧几里得
求最大公约数的一种常用方法
public static int gcd(int a, int b) {return b != 0 ? gcd(b, a % b) : a;
}
二、扩展欧几里得
求x,y使得ax+by = gcd(a,b)
public static int exGcd(int a,int b,int x,int y){if(b == 0){x = 1;y = 0;return a;}int d = exGcd(b,a%b,y,x);y -= (a/b)*x;return d;}
三、算术基本定理
算术基本定理,又称为正整数的唯一分解定理,即:每个大于1的自然数,要么本身就是质数,要么可以写为2个或以上的质数的积,而且这些质因子按大小排列之后,写法仅有一种方式。

证明参考:维基百科
四、线性筛选求质数
在O(N)的时间复杂度内,求出来1 ~ n中所有的质数,以及每一个数的最小质因子。
private static void get_primes(int n) {for (int i = 2; i <= n; i++) {if (!st[i]) primes[cnt++] = i;for (int j = 0; primes[j] * i <= n; j++) {/*因为prime中素数是递增的,所以如果i%prime[j]!=0代表i的最小质因数还没有找到,即i的最小质因数大于prime[j]也就是说prime[j]就是i*prime[j]的最小质因数,于是i*prime[j]被它的最小质因数筛掉了*/st[primes[j] * i] = true; // 把质数的i倍筛掉/*如果当i%prime[j]==0时,代表i的最小质因数是prime[j],那么i*prime[j+k](k>0)这个合数的最小质因数就不是prime[j+k]而是prime[j]了所以i*prime[j+k]应该被prime[j]筛掉,而不是后续的prime[j+k],于是在此时break*/if (i % primes[j] == 0) break; // 通过最小质因子来筛}}}
五、等差数列
这俩个数列,学过高中数学的应该都清楚,我就不加以证明了。
1246. 等差数列
import java.util.Arrays;
import java.util.Scanner;/*** @Author 秋名山码神* @Date 2023/2/17* @Description*/
public class Main {static int N = 100010;static int[] a = new int[N];public static int gcd(int a,int b){return b != 0 ? gcd(b,a%b) : a;//b!=0 , 递归计算gcd(b,a%b)}public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();for(int i = 0; i<n; i++)a[i] = sc.nextInt();Arrays.sort(a,0,n);int d = 0;for(int i = 1; i<n; i++)d = gcd(d,a[i] - a[0]);if(d == 0){System.out.println(n);}else {System.out.println((a[n-1] - a[0]) / d + 1);}}
}六、等比数列
P8636 蓝桥杯 2016 省 AB 最大比例
#include<iostream>
#include<algorithm>using namespace std;const int N=110;typedef long long LL;LL x[N],a[N],b[N];
int cnt=0;//假设原数列为 a,a*(p/q)^1,a*(p/q)^2,...,a*(p/q)^(n-1)
//假设抽取的数列 b0,b1,...,b(N-1) (从小到大排好序了)
// b1/b0,b2/b0,...,b(N-1)/b0--> (p/q)^x1,(p/q)^x2,...,(p/q)^x(N-1)
// 我们要求的是: (p/q)^k (p/q)>1,所以使k最大,即求 x1~x(N-1)的最大公约数
//这里我们使用更相减损术,因为我们没有得到确切的x1~x(N-1)是多少,我们只有(p/q)^x1,(p/q)^x2,...,(p/q)^x(N-1)这些的值/*更相减损术:第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2的积与第二步中等数的乘积就是所求的最大公约数。*///更相减损术总用较大的减去较小的
/*例子:98-63=3563-35=2835-28=728-7=2121-7=1414-7=7
所以,98和63的最大公约数等于7。*///我们这里要用更相减损术的是指数,所以要让(p/q)^x1,(p/q)^x2,...,(p/q)^x(N-1),两两计算,互除,除到结果为1,即x1=x2,此时幂次为0,结果为1,这其实就是y总的思路,再次感叹y总的才华
//把分子分母分别去算,结果是相同的因为,分子分母的幂次是相同的
LL gcd(LL a,LL b)
{return b? gcd(b,a%b):a;
}LL gcd_sub(LL a,LL b)
{if(a<b) swap(a,b); //更相减损术总是大减小(它们的底数是一样的)if(b==1) return a;return gcd_sub(b,a/b);
}int main()
{int n;cin>>n;for(int i=0; i<n; i++) scanf("%lld",&x[i]);sort(x,x+n);for(int i=1; i<n; i++){if(x[i] != x[i-1]){LL d=gcd(x[i],x[0]); a[cnt]=x[i] / d; //得到x[i]/x[0]的分子b[cnt]=x[0] / d; //得到x[i]/x[0]的分母cnt++;}}LL up=a[0],down=b[0];for(int i=1; i<cnt; i++){up=gcd_sub(up,a[i]); //两两求最大公约数down=gcd_sub(down,b[i]);}cout<<up<<"/"<<down<<endl;return 0;
}
七、组合计数
加法原理 : 若完成一件事的方法有n类,其中第i类方法包括ai种不同的方法,且这些方法互不重合,则完成这件事共有a1+a2+…+an种不同的方法。
乘法原理 :若完成一件事,需要n个步骤,其中第i个步骤有ai种不同的完成方法,且这些步骤互不干扰,则完成这件事共有a1a2…*an种不同的方法
排列数 : 从n个不同的元素中依次取出m个元素排成一列,产生的不同排列的数量为:

组合数 : 从n个元素中取出m个元素组成一个集合(不考虑顺序),产生的不同集合的数量为:
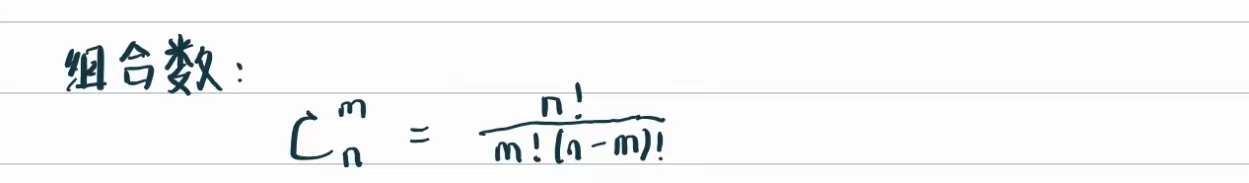
计算系数
//杨辉三角做法:
#include<iostream>
using namespace std;
long long x[1010][1010];
int main()
{long long a,b,k,n,m;cin>>a>>b>>k>>n>>m;x[1][1]=1;for(int i=2;i<=k+1;i++) for(int j=1;j<=i;j++)x[i][j]=(x[i-1][j-1]*b+x[i-1][j]*a)%10007;cout<<x[k+1][m+1];return 0;
}
二项式做法
最后
数论的知识太多了,这是我最近三天想到的,后续有时间再补充吧!

相关文章:

算法比赛——必备的数论知识
秋名山码民的主页 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 🙏作者水平有限,如发现错误,还请私信或者评论区留言! 目录一、欧几里得二、扩展欧几里得三、算术基本定理四、线性筛选求质数五…...
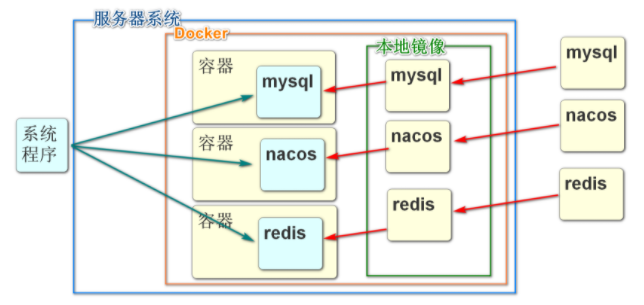
Docker概述
什么是Docker我们要学习在Linux(RockyLinux)中安装使用Docker来配置软件的功能Docker是一个用来开发、运输和运行应用程序的开放平台。使用Docker可以将应用程序与基础结构分离,以便快速交付软件。使用Docker,您可以以管理应用程序的方式管理基础架构。通…...

实验室设计建设方案主要内容
实验室设计建设整体解决方案SICOLAB需要综合考虑实验室的功能需求、空间布局、设备选型、安全防护、节能环保等多方面因素。以下是一个基本的实验室设计建设方案的流程:一、需求分析:了解实验室的使用目的、实验内容、使用人数、设备种类、实验标准等&am…...
)
华为OD机试真题Python实现【日志采集系统】真题+解题思路+代码(20222023)
日志采集系统 题目 日志采集是运维系统的的核心组件。日志是按行生成,每行记做一条,由采集系统分批上报。 如果上报太频繁,会对服务端造成压力; 如果上报太晚,会降低用户的体验; 如果一次上报的条数太多,会导致超时失败。 为此,项目组设计了如下的上报策略: 每成功上…...

Python的模块与工具包
模块 模块是一个Python文件,以 .py结尾。模块能定义函数,类和变量,模块里也能包含可执行的代码。 作用 python 中有很多各种不同的模块,每一个模块都可以帮助我们快速的实现一些功能,比如实现和时间相关的功能就可以…...

联合熵和条件熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录联合熵条件熵联合…...
)
华为OD机试真题Python实现【求最大数字】真题+解题思路+代码(20222023)
求最大数字 题目 给定一个由纯数字组成以字符串表示的数值,现要求字符串中的每个数字最多只能出现2次,超过的需要进行删除;删除某个重复的数字后,其它数字相对位置保持不变。 如34533,数字3重复超过2次,需要删除其中一个3,删除第一个3后获得最大数值4533 请返回经过删…...

Python爬虫(10)selenium爬虫后数据,存入csv、txt并将存入数据并对数据进行查询
之前的文章有关于更多操作方式详细解答,本篇基于前面的知识点进行操作,如果不了解可以先看之前的文章 Python爬虫(1)一次性搞定Selenium(新版)8种find_element元素定位方式 Python爬虫(2)-Selenium控制浏览…...
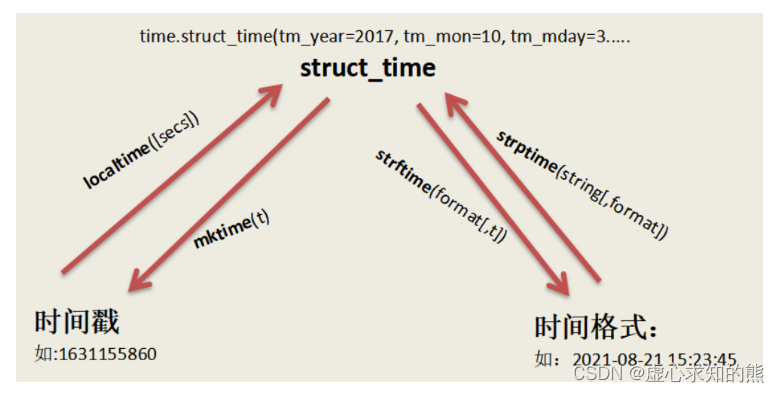
Python 之 Pandas 时间函数 time 、datetime 模块和时间处理基础
文章目录一、time 模块1、时间格式转换图2. struct_time 元组元素结构3. format time 结构化表示二、datetime 模块1. date类2. 方法和属性3. datetime 类三、timedelta 类的时间加减四、时间处理基础Python 中提供了对时间日期的多种多样的处理方式,主要是在 time …...

C语言学习及复习笔记-【5】C 运算符
文章目录5. C 运算符5.1 关系运算符5.2 逻辑运算符5.3 位运算符5.4 杂项运算符 ↦ sizeof & 三元5.5 例子1). 利用异或 ^ 来交换两个数的值,而且不引入其他变量。2). 利用位与 & 运算,判断一个整数是否是2的整数次幂。3). 不同长度的数据进行位运…...
数仓、数据湖、湖仓一体、数据网格
第一代:数据仓库 定义 为解决数据库面对数据分析的不足,孕育出新一类产品数据仓库。数据仓库(Data Warehouse)是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持管理决策和信息的全局共享。 数…...

C语言【atoi函数】
C语言【atoi函数】🫅系统atoi函数🫅 模拟实现atoi函数看到atoi函数,有人又会问有这个函数,我怎么没用过。那就说明:不是你刷题太少,就是atoi函数存在感太低。 这篇函数就带你领略atoi函数的魅力 Ǻ…...

一起学习用Verilog在FPGA上实现CNN----(八)integrationFC设计
1 integrationFC设计 LeNet-5网络结构全连接部分如图所示,该部分有2个全连接层,1个TanH激活层,1个SoftMax激活层: 图片来自附带的技术文档《Hardware Documentation》 integrationFC部分原理图,如图所示,…...

面试题总结
1.js的数据类型 分为基本数据类型和引用数据类型。 基本数据类型 ES5的5种:Null,undefined,Boolean,Number,String, ES6新增:Symbol表示独一无二的值 ES10新增:BigInt 表示任意大的…...
go进阶(1) -深入理解goroutine并发运行机制
并发指的是同时进行多个任务的程序,Web处理请求,读写处理操作,I/O操作都可以充分利用并发增长处理速度,随着网络的普及,并发操作逐渐不可或缺 一、goroutine简述 在Golang中一个goroutines就是一个执行单元ÿ…...

mongodb 操作记录
#启动服务 net start MongoDB #停止服务 net stop MongoDB #进入mongo shell 方式 mongo db #查看当前数据库是那个 #插入一条数据 db.runoob.insert({x:10}) #查找数据 db.runoob.find() 查询所有的数据库 show dbs #连接mongodb mongodb://[username:password]host1[:po…...

JDBC简单的示例
JDBC 编程步骤 加载驱动程序: Class.forName(driverClass) //加载MySql驱动 Class.forName("com.mysql.jdbc.Driver") //加载Oracle驱动 Class.forName("oracle.jdbc.driver.OracleDriver")获得数据库连接: DriverManager.getCon…...
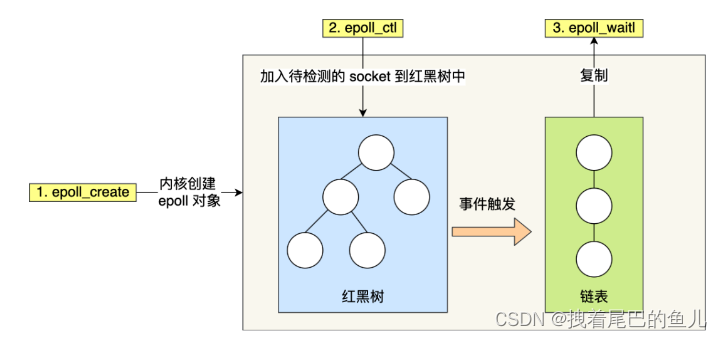
Spring架构篇--2.3 远程通信基础--IO多路复用select,poll,epoll模型
前言:对于传统的BIO(同步阻塞)模型,当有客户端连接达到服务端,服务端在对改连接进行连接建立,和数据传输过程中,是无法响应其他客户端的,只有当服务端完成对一个客户端处理后&#x…...
python--matplotlib(4)
前言 Matplotlib画图工具的官网地址是 http://matplotlib.org/ Python环境下实现Matlab制图功能的第三方库,需要numpy库的支持,支持用户方便设计出二维、三维数据的图形显示,制作的图形达到出版级的标准。 其他matplotlib文章 python--matpl…...
)
【项目精选】城市公交查询系统(论文+视频+源码)
点击下载源码 1.1 选题背景 随着低碳生活的普及,人们更倾向于低碳环保的出行方式,完善公交系统无疑具有重要意义。公交是居民日常生活中最常使用的交通工具之一,伴随着我国经济繁荣和城市人口增长,出行工具的选择也变得越来越重要…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...
