【备战csp-j】 csp常考题目详解（4）
四.数值转换与编码
1. 十进制数 11/128 可用二进制数码序列表示为( ) 。
A.1011/1000000
B.1011/100000000
C.0.001011
D.0.0001011
答案：D
解析：暂时未找到解决方法，以后会解决。
2. 算式(2047)10 － (3FF)16 ＋ (2000)8 的结果是( ) 。
A.(2048)10
B.(2049)10
C.(3746)8
D.(1AF7)16
答案：A
解析：经计算可知结果为A
3. [x]补码=10011000，其原码为( ) 。
A.011001111
B.11101000
C.11100110
D.01100101
答案：B
解析：补码=原码取反+1；所以反推可得反码为补码-1也就是10010111，符号位不变，所以接着反推原码也就是反码取反等于11101000，故选B。
4. (2004)10 + (32)16 的结果是（ ）。
A.(2036)10
B.(2054)16
C.(4006)10
D.(100000000110)2
答案：D
解析：由于答案中有两个是十进制，所以我们优先把两个数都转为十进制。2004本来就是十进制，所以不变，而16进制的32转换为十进制就是3*16的一次方+2*16的零次方也就是48+2等于50。随后把两个数加起来得2054，可我们发现十进制没有2054这个选项，而16进制的2054不可能等于10进制的2054。所以结果只能为D
5. 十进制数 100.625 等值于二进制数（ ）。
A.1001100.101
B.1100100.101
C.1100100.011
D.1001100.11
答案：B
解析：小数部分乘二取整，整数部分除二取余，所以整数部分=1100100，而小数部分则为0.625*2取整得1，0.25乘二取整得0，0.5乘二正好等于1，所以结束。结果为1100100.1
01。也就是B。
相关文章：
【备战csp-j】 csp常考题目详解（4）
四.数值转换与编码 1. 十进制数 11/128 可用二进制数码序列表示为( ) 。 A.1011/1000000 B.1011/100000000 C.0.001011 D.0.0001011 答案：D 解析：暂时未找到解决方法，以后会解决。 2. 算式(2047)10 － (3FF)16 ＋ …...
linux中常见服务端安装
linux安装服务脚本 1、yum安装 # 通过apt安装yum apt install yum # yum安装软件 yum install pam-devel # yum 卸载 yum remove pam-devel2、rpm安装 # 安装 rpm -i example.rpm #安装 example.rpm 包； rpm -iv example.rpm #安装 example.rpm 包并在安装过程…...
L1-058 6翻了(Python实现) 测试点全过
前言： {\color{Blue}前言：} 前言： 本系列题使用的是，“PTA中的团体程序设计天梯赛——练习集”的题库，难度有L1、L2、L3三个等级，分别对应团体程序设计天梯赛的三个难度。更新取决于题目的难度，…...
初学Python记
Python这个编程语言的大名当然听说过了呀，这几年特别火，火的一塌涂地。大家可以回忆一下：朋友圈推荐的广告里经常可以看见python的网课广告。 本学期，学校开设了python课程，这几天学习了一下入了一下门，感…...
计算机竞赛 基于深度学习的目标检测算法
文章目录 1 简介2 目标检测概念3 目标分类、定位、检测示例4 传统目标检测5 两类目标检测算法5.1 相关研究5.1.1 选择性搜索5.1.2 OverFeat 5.2 基于区域提名的方法5.2.1 R-CNN5.2.2 SPP-net5.2.3 Fast R-CNN 5.3 端到端的方法YOLOSSD 6 人体检测结果7 最后 1 简介 ǵ…...
sentinel-core
引入依赖<dependencies><dependency><groupId>com.alibaba.csp</groupId><artifactId>sentinel-core</artifactId></dependency><dependency><groupId>com.alibaba.csp</groupId><artifactId>sentinel-anno…...
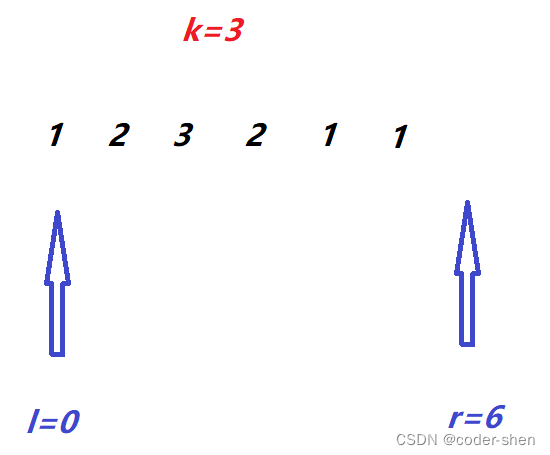
【美团3.18校招真题1】
大厂笔试真题网址：https://codefun2000.com/ 塔子哥刷题网站博客：https://blog.codefun2000.com/ 小美剪彩带 提交网址：https://codefun2000.com/p/P1088 题意：找出区间内不超过k种数字子数组的最大长度 使用双指针的方式&…...
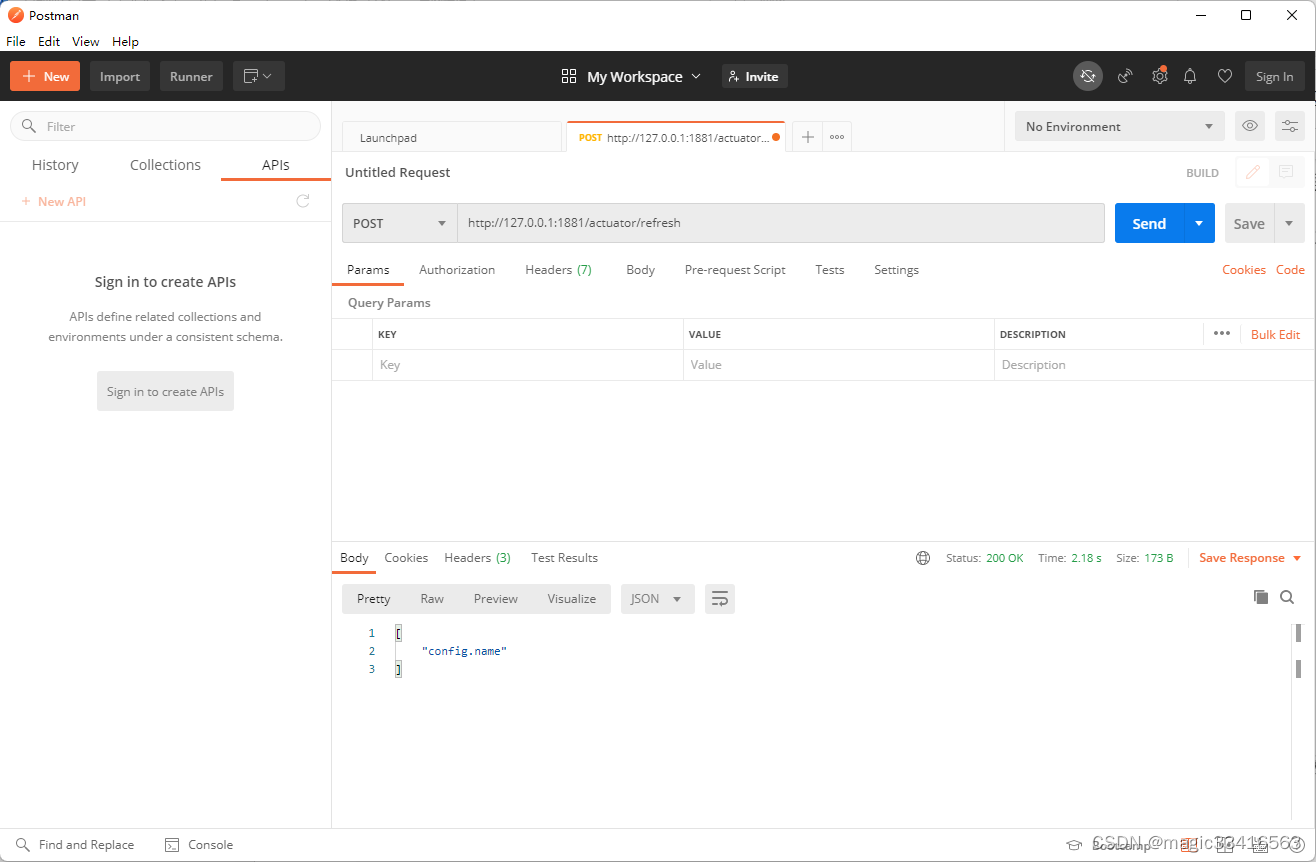
Springboot 实践（14）spring config 配置与运用--手动刷新
前文讲解Spring Cloud zuul 实现了SpringbootAction-One和SpringbootAction-two两个项目的路由切换，正确访问到项目中的资源。这两个项目各自拥有一份application.yml项目配置文件，配置文件中有一部分相同的配置参数，如果涉及到修改…...
MyBatisPlus枚举类最佳实践（非常典型和高效的枚举类写法）
目录 1、MyBatisPlus枚举类最佳实践 2、枚举类的作用及问题 3、MyBatisPlus注解实现枚举最佳实践 4、简单来说 5、下面我们看一个使用上述注解的完整枚举类示例: （1）枚举类： （2）DTO类： 6、根据上面…...
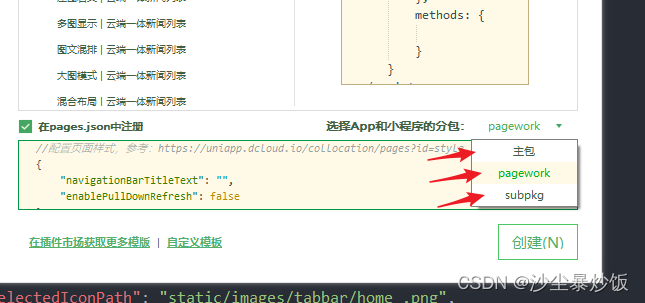
uniapp分包 解决分多个包的问题
1. 分包可以分很多个, 但是在"optimization": { "subPackages": true } 里面只能写一个, 2. 想分多个包 , 在 pages.json 里面 的 subPackages 里面继续加 第三个 第四个即可 3. 保存之后 创建页面就可以看见多个包了...
美国封锁激励中国制造业数字化转型的崛起 | 百能云芯
上海在近日公布了第二批工赋链主培育企业名单，共有15家企业入选。这些被称为“链主”的企业在上海制造业数字化转型的过程中扮演着关键角色，类似于领头大雁，它们是上海制造业的数字化网络中的关键节点。 中新社的报道指出，“数字技…...
鼠标键盘自动化工具pyautogui
安装 pip install pyautogui pip install keyboard获取鼠标实时位置 import pyautogui pyautogui.displayMousePosition()样例代码 # https://pyautogui.readthedocs.org/ # https://github.com/asweigart/pyautogui# 紧急停止，手动将鼠标移动到屏幕的4个角落imp…...
0基础学习VR全景平台篇 第96篇：VR电子楼书
大家好，欢迎观看蛙色VR官方系列课程——VR电子楼书！ 作为2021年底全新上线的行业解决方案，是专门针对地产、园区数字化营销的一站式VR解决方案，为行业潜在客户提供优质的7x24小时线上看房体验。 本期教程将通过功能介绍后台操作&…...
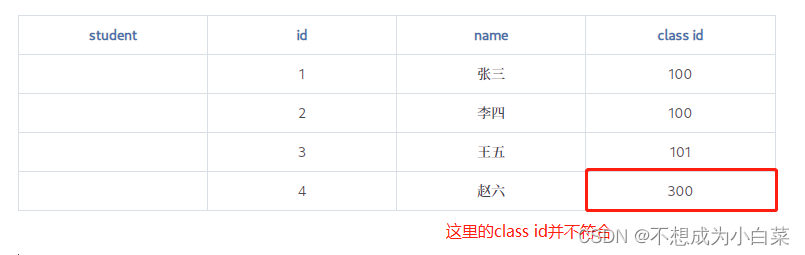
【MySQL】数据库的约束
MySQL 数据库的约束 文章目录 MySQL 数据库的约束01 数据库的约束1.1 约束类型1.1.1 NOT NULL1.1.2 UNIQUE1.1.3 DEFAULT1.1.4 PRIMARY KEY1.1.5 FOREIGN KEY1.1.6 CHECK 继上文 MySQL基础（一）， MySQL基础（二）&#…...
改变金融贷款市场营销方式 ---- 运营商大数据精准获客
与传统的企业网络营销相比，最常见的是网络推广和硬广告推广。一些企业无法找到可靠准确的数据来源，也无法找到一些未知的总数据。这些数据大多存在持续时间长、准确性差的缺点，企业在将这些数据信息应用于商品在线营销时往往会遇到不足。 在…...
SpringBoot实现分页的四种方式
一 自己封装Page对象实现 博客链接 二 使用sql实现分页 2.1 场景分析 前段传递给给后台什么参数? 当前页码currentPage每页显示条数pageSize 后台给前端返回什么数据? 当前页数据List总记录数totalCount 2.2 前段代码 <template><el-paginationsize-change&q…...
远程工作面试：特殊情况下的面试技巧
🌷🍁 博主猫头虎（🐅🐾）带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
element ui文件上传方法中需要传额外参数
由于文件上传dom是通过循环列表渲染的，在文件上传的时候除了file默认的参数外，还需要访问到循环项item参数，那就这样子传递。 :http-request"(file) > {return httpRequestLT(file, item);} "完整代码如下 <div class"…...
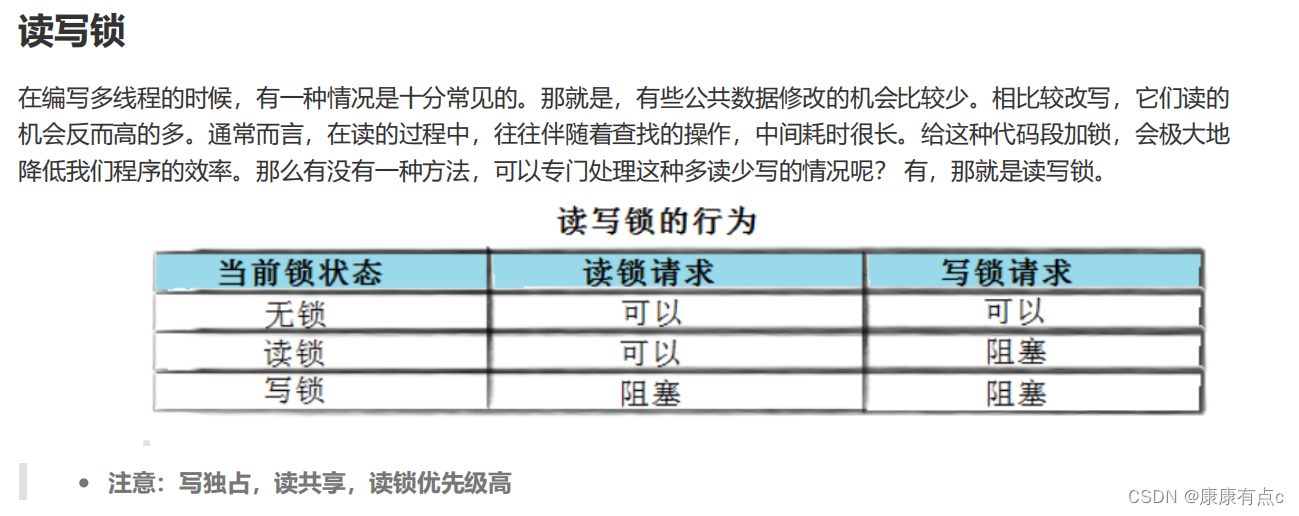
线程池|单例模式|STL、智能指针线程安全|读者写者问题
线程池 线程池的逻辑思想： 每当我们处理一个任务就要创建一个线程，创建线程的开销是很大的。因此我们可以预先创建一批线程，任务队列里没有任务的时候，每个线程都休眠，当队里中有任务的时候，就可以唤醒线程…...
Linux的基本使用和Web程序部署（JavaEE初阶系列18）
目录 前言： 1.Linux 1.1Linux是什么 1.2Linux发行版 1.3Linux环境搭建 1.3.1环境搭建方式 1.3.2使用云服务器 1.4使用终端软件连接到Linux 1.4.1什么是终端软件 1.4.2使用Xshell登录主机 1.5Linux常用的命令 1.5.1ls 1.5.2cd 1.5.3pwd 1.5.4touch 1.…...
Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
如何在最短时间内提升打ctf（web)的水平？
刚刚刷完2遍 bugku 的 web 题，前来答题。 每个人对刷题理解是不同，有的人是看了writeup就等于刷了，有的人是收藏了writeup就等于刷了，有的人是跟着writeup做了一遍就等于刷了，还有的人是独立思考做了一遍就等于刷了。…...
听写流程自动化实践，轻量级教育辅助
随着智能教育工具的发展，越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式，也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建，…...
QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...
在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1： 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置： // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存：一级缓存、二级缓存 默认情况下，只有一级缓存开启（sqlSession级别的缓存）二级缓存需要手动开启配置，需要局域namespace级别的缓存 一级缓存（本地缓存&#…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一：yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因，后面把yaml.safe_dump直接替换成yaml.dump，确实能保存，但出现乱码： 放弃yaml.dump，又切…...
AD学习（3）
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分： （1）PCB焊盘：表层的铜 ，top层的铜 （2）管脚序号：用来关联原理图中的管脚的序号，原理图的序号需要和PCB封装一一…...